巧用“八字大法”学函数

杨永康

(广东省惠州市惠阳区第四中学,广东 惠州 516000)

巧用“八字大法”学函数

杨永康

(广东省惠州市惠阳区第四中学,广东 惠州 516000)

函数的“八字大法”是笔者多年教学经验的总结，是在新课标下师生互动的产物.“八字大法”的思想实质是数形结合，几乎适用于所有函数性质的学习与应用.“八字大法”即在平面直角坐标系xOy中，所有函数图像如果位置形如“八”字左边“丿”部分，都是y随x的增大而增大；反之亦然。形如“八”字右边“”部分，都是y随x的增大而减小，反之亦然.至于“八字大法”应用的细化，本文将以具体函数为例作探究.

杨氏八字大法；函数；数形结合

一次函数、反比例函数和二次函数是初中数学的重要组成部分，是衔接高中数学函数知识的基础，因此在各类考试选拔中分量不轻，但很多学生对函数知识的学习却是心有余而力不足.究其原因，是不善探究，学不得法.

学习函数的“八字大法”是笔者多年教学经验的总结，是在新课标下师生互动的产物.教学上，笔者对学生戏称“杨氏八字大法”，这样可激发学生的学习兴趣，提高效果.

“八字大法”的思想实质是数形结合.即在平面直角坐标系xOy中，所有函数图象如果位置形如“八”字左边“丿”部分，都是y随x的增大而增大；反之亦然.形如“八”字右边“”部分，都是y随x的增大而减小，反之亦然.至于“八字大法”应用的细化，下面将以具体函数为例作探究.

一、对于一次函数y=kx+b(k≠0)而言，其图象是直线，位置形如“八”字左边“丿”部分，都是k>0，且y随x的增大而增大，图象必经过第一、三象限；反之亦然.形如“八”字右边“”部分，都是k<0，且y随x的增大而减小，图象必经过第二、四象限；反之亦然.至于图象经过的另一个象限，则由截距b确定：当b>0时，直线交y轴于正半轴；当b<0时，直线交y轴于负半轴；当b=0(此时函数为正比例函数)时，直线经过原点.

例1 若一次函数y=kx+b的函数值y随x的增大而减小，且图象与y轴的正半轴相交，那么对k和b的符号判断正确的是( ).

A．k>0，b>0 B．k>0，b<0 C．k<0，b>0 D．k<0，b<0

解析 本题中函数值y随x的增大而减小，由“八字大法”，其图象形如“八”字右边“”部分，则k<0，而图象与y轴的正半轴相交，b>0，图象交于y轴的正半轴，答案选C.

例2 一次函数y=-x+2的图象是( ).

解析 本题中k=-1<0，由“八字大法”，其图象形如“八”字右边“”部分，故选择答案时可排除A、B，而b=2>0，图象交于y轴的正半轴，所以答案选D.

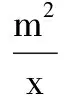
A．第一、二象限 B．第一、三象限

C．第二、四角限 D．第三、四象限

解析 本题中k=-m2<0，由“八字大法”，其图象形如“八”字左边“丿”部分，则其图象必经过第二、四象限，所以答案选C.

例4 若二次函数y=ax2+bx+c的图象如右图所示，①当____时，y随x值的增大而增大；②当____时，y随x值的增大而减小.

解析 本题可根据所给数据求出抛物线的对称轴为直线x=1，因为函数图象的开口向上，由“八字大法”， 对称轴左边即x<1的图象，位置形如“八”字右边“”部分，y随x的增大而减小；对称轴右边即x>1的图象，位置形如“八”字左边“丿”部分，y随x的增大而增大，所以答案为①x>1，②x<1.

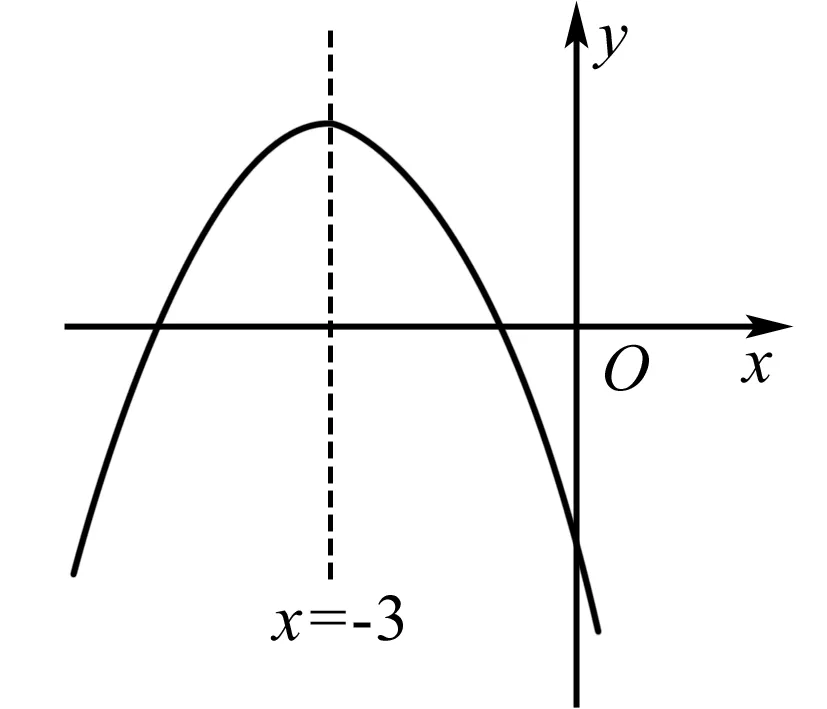
例5 二次函数y=ax2+bx+c的图象如图所示，若点A(1，y1)、B(2，y2)是它图象上的两点，则y1与y2的大小关系是( ).

A．y1

C．y1>y2D．不能确定

解析 本题可根据图形知道抛物线的对称轴为直线x=-3.因为函数图象的开口向下，x1=1、x2=2都在对称轴直线x=-3的右边，由“八字大法”， 对称轴右边即x>-3的图象，位置形如“八”字右边“”部分，y随x的增大而减小，因为x1y2，故本题答案选C.

A．y1

解析 本题难度较上面两例大一点，因为所给的三个点分布在对称轴的两边，我们可以根据抛物线的对称性将三个点放在对称轴的同一边，再画出草图，结合图象利用“八字大法”解决问题.

综上所述，利用“八字大法”进行初中数学函数知识的教与学，既简单实用又能激发学生的学习兴趣，从而提高学生的分析、总结和解题能力，使他们能在学习中快乐地掌握知识并能灵活运用，所谓学以致用且有效，这符合新课标的要求.同时，“八字大法”还可以运用在规则或者不规则的函数应用上，此问题留给读者探究.

[1]舒亚明.待定系数法[J].青少年日记(教育教学研究)，2011(10).

[责任编辑：李克柏]

2017-06-01

杨永康，男，党员，研究生学历.从事数学基础教育.

G632

B

1008-0333(2017)20-0022-02