岩土小样本参数区间估计方法探讨

李化云，范洪海，胡 端

(1.西华大学建筑与土木工程学院，四川成都610039；2.西华大学绿色建筑与节能重点实验室，四川成都610039；3.中国港湾工程有限公司，北京100027；4.西南交通大学交通隧道工程教育部重点实验室，四川成都610031)

岩土小样本参数区间估计方法探讨

李化云1，2，范洪海3，胡 端4

(1.西华大学建筑与土木工程学院，四川成都610039；2.西华大学绿色建筑与节能重点实验室，四川成都610039；3.中国港湾工程有限公司，北京100027；4.西南交通大学交通隧道工程教育部重点实验室，四川成都610031)

岩土参数分布区间的计算是可靠度分析方法中的一项基础性工作。在实际工程中，受采样数量的限制，岩土参数多为小样本。在探讨3σ法则、考虑偏度的分布区间修正法以及非参数Bootstrap法等现有的岩土小样本参数区间估计方法的适用情形及存在的不足的基础上，结合岩土工程参数区间估计的特点，提出了一种适用于小样本岩土参数区间估计的改进灰自助法。算例表明，在不同的参数分布情形及样本数量下，改进方法优于已有方法。

岩土工程；小样本；参数；区间估计

0 引 言

近年来，以可靠度分析方法为代表的不确定分析方法在岩土工程领域得到快速发展。岩土参数分布区间的计算是可靠度分析方法中的一项基础性工作，但由于取样数目受试验周期、难度以及费用等因素的限制，通常仅能获取少量的样本。通过小样本合理地确定岩土参数分布区间，对发展和完善可靠度分析方法体系有着重要意义[1-5]。为此，研究者们发展了多种方法，如将正态分布中著名的3σ法则用于岩土参数分布区间估计，该方法是以岩土参数服从正态分布为前提的，而实际中的岩土参数常常并不满足正态分布，而且该方法没有考虑实际分布具有一定偏度的特点；宫凤强和黄天朗等[6]提出了一种考虑偏度的分布区间修正法，在一定程度上改善了3σ法的不足；骆飞等[7]则将对领域区间进行扩展的改进非参数Bootstrap法用于求解参数分布区间，但当样本容量过小时，其扩展范围是很有限的；此外，还有诸如t分布等理论概率方法也被用于确定岩土参数分布区间。一般来说，在岩土工程中，实测岩土参数分布区间[xmin，xmax]应包含在估计区间[a，b]内，而上述方法所得结果常常并不满足，且目前仍然缺乏有效的方法确定区间[a，b]的上下限。

鉴于目前该问题研究存在的不足，本文将灰自助法用于确定岩土参数分布区间，并针对岩土参数的特征，对灰自助法进行了改进，提出了岩土参数区间估计的改进灰自助法。

1 岩土参数区间估计方法

1.1 正态分布(3σ法)

该方法以岩土参数服从正态分布为前提，通过正态分布中常用的3σ法则确定a，b，即

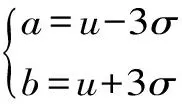
(1)

式中，u为均值，σ为方差。

理论上，若参数服从正态分布，则该方法的置信概率为99.74%，即参数取值分布在该区间的概率为99.74%。然而，大量的统计结果表明，岩土参数并非都服从于正态分布，如有学者认为粘聚力和内摩擦角服从对数正态分布。此外，理论正态分布的概率密度曲线具有分布对称的特征，岩土参数的实际分布却具有一定的偏度，且直接采用式(1)计算可能会得出负值，这与岩土参数物理意义不符。

1.2 考虑偏度的分布区间修正法

为避免经典的3σ法不能考虑偏度的不足，宫凤强等提出了一种考虑偏度的分布区间修正法，其计算式如下

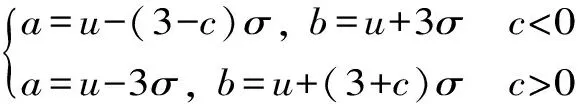
(2)

式中，c表示偏度，且当u-(3-c)σ<0或u-3σ<0，取a=0。该方法所得估值区间比式(1)要大。笔者认为，虽然该方法考虑了偏度的影响，但其仍然更适合于正态分布情形。

1.3 Bootstrap法

已经证明，Bootstrap法是处理小样本数据的一种行之有效的手段。其中，非参数Bootstrap法已被用来解决岩土参数区间估计问题。该方法实质上是将小样本数据通过放回抽样等扩展为大样本数据。标准的非参数Bootstrap法完全通过放回抽样对样本进行扩展，从而完成区间估值。因而得到的分布区间[a，b]往往包含在[xmin，xmax]之内，这显然不能直接用于岩土工程中的区间估计问题。骆飞等[7]通过改进的非参数Bootstrap法完成对分布区间的扩展，一定程度上避免了上述不足，但当样本容量很少时，其扩散范围是很有限的。

2 改进灰自助法

由于标准的非参数Bootstrap法完全通过放回抽样，对样本进行扩展从而完成区间估值。自助样本完全由原样本产生，当已知样本容量较小时，自助样本与已知样本极为相似，得到的结果偏离真实分布，存在较大的误差。本文给出一种简单的改进非参数Bootstrap法。

设试验所得岩土参数数据为x1，x2，…，xn(已将参数升序排序)。按下式对抽样数据进行扩展

xs=xi+rand(xi+1-xi)

(3)

式中，i=1，2，…，n-1。式(3)实质上是对经验分布函数进行插值。按式(3)进行抽样，得到1个Bootstrap样本，重复多次，即可得到多个Bootstrap样本。

对每个Bootstrap样本进行升序排序，通过灰色预测模型得到每个Bootstrap样本的下1个预测值xn+1，该预测值可以看作是对Bootstrap样本的右区间的延伸。同理，对每个Bootstrap样本降序排序，通过灰色预测模型又可以得到1个预测值x0，将该预测值视为Bootstrap样本的左区间的延伸。由此可以完成对每个Bootstrap样本的区间边界的扩展。值得说明的是，该扩展方法是建立在灰色预测模型对小样本数据良好的适应性之上的，能够避免人为主观进行扩展的不足。灰色模型的建立与求解描述如下[8-9]：

对每个Bootstrap样本进行累加生成并按均值生成法构造背景值，即

(4)

式中，Y为x1，x2，…，xi相加的和，Z为背景值函数。

建立白化方程

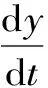
(5)

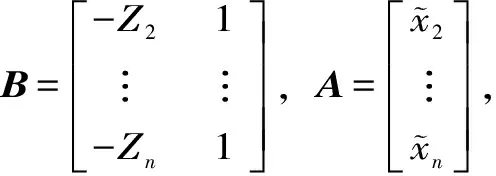
[ab]T=(BTB)-1BTA

(6)

从而可得到式(5)的时间响应序列解为

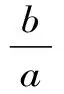
(7)

通过累减还原的方法可以得到预测值。

将m个Bootstrap样本右区间延伸值的集合记为{xn+1(i)}(i=1，2，…，m)；左区间延伸值的集合记为{x0(i)}(i=1，2，…，m)。考虑到在岩土工程中，实测岩土参数分布区间[xmin，xmax]应包含在估计区间[a，b]之内，按如下方式确定估计区间：

(1)右边界。判断xn+1(i)与xmax的大小，取出{xn+1(i)}中所有大于等于xmax的元素，组成1个新集合{xnew(i)}，取新集合元素的平均值作为b的估计。

(2)左边界。判断x0(i)与xmin的大小，取出{x0(i)}中所有小于等于xmin的元素，组成1个新集合{xnew1(i)}，取新集合元素的平均值作为a的估计。

3 工程算例

3.1 不同分布情况下的参数区间估计

分别比较在正态分布、对数正态分布、威布尔分布、贝塔分布、均匀分布情况下几种方法的区间估计效果。取孔隙比、液限、粘聚力、酸蚀岩体强度、塑限等5个岩土参数的实测数据作为区间估计的样本。孔隙比的样本容量为26个，满足正态分布，各实测值分别为0.802、0.964、1.041、1.057、1.105、1.185、1.195、1.206、1.215、1.224、1.227、1.244、1.246、1.263、1.278、1.297、1.325、1.328、1.343、1.390、1.394、1.454、1.492、1.537、1.641、1.699；液限的样本容量为26个，满足对数正态分布，各实测值分别为36.9%、37.2%、37.9%、42.1%、44.7%、45.2%、47.2%、47.3%、48.5%、48.5%、48.5%、48.5%、48.6%、48.7%、51.0%、52.0%、52.6%、53.5%、53.8%、55.3%、56.0%、56.0%、57.5%、58.9%、66.5%、69.5%；粘聚力的样本容量为21个，满足贝塔分布，各实测值分别为7.2、8.8、9.1、9.2、9.2、10.8、12.3、12.3、12.8、15.4、15.4、16.0、16.4、16.9、16.9、16.9、17.6、19.1、20.0、21.6 kPa和23.1 kPa；酸蚀岩体强度的样本容量为19个，满足威布尔分布，各实测值分别为134、153、119、156、122、146、107、120、114、128、148、141、142、147、130、92、167、113 MPa和127 MPa；塑限的样本容量为23个，满足均匀分布，各实测值分别为18.9%、19.4%、20.8%、20.8%、21.3%、21.6%、22.1%、22.6%、22.9%、23.3%、23.3%、24.1%、24.4%、25.2%、25.5%、25.5%、26.1%、26.5%、27.5%、28.2%、28.3%、28.4%、28.7%。分别应用本文方法、3σ法以及考虑偏度的分布区间修正法对数据进行参数区间估计，所得结果见表1。为了进行直观对比，图1给出了各种方法的计算上下限和实测参数的上下限的对比。由表1和图1可知，通常情况下，3σ法则和考虑偏度的分布区间修正法得到的估计区间大于实测参数区间，且这2种方法得到的估计区间差别不大。相比之下，本文方法得到的估计区间略大于实测参数分布区间而又小于其他2种方法所得的估计区间。此外，在正态分布情形下，3σ法及考虑偏度的分布区间修正法得到的估值区间较实测参数区间差别不大，但当处于其他几种分布情形下时，这2种方法得到的估值区间都较实测区间有较大差距，尤其是在贝塔分布情形下，这2种方法的计算结果较实测参数上下限差别最大。相比之下，本文的方法无论在哪种情形下的计算结果都能与实测参数较为保持一致。

3.2 不同样本数量的参数区间估计

为了检验几种方法在不同样本数量的参数区间估计时的应用效果，分别取不同数量的岩土参数内摩擦角正切值实测数据。组1的样本容量为25个，各实测值分别为0.21、0.25、0.24、0.18、0.20、0.23、0.22、0.24、0.23、0.28、0.29、0.31、0.38、0.38、0.48、0.41、0.46、0.49、0.42、0.36、0.32、0.38、0.37、0.37、0.52；组2的样本容量为42个，各实测值分别为1.14、1.19、1.06、1.80、1.48、1.48、1.55、0.94、0.68、0.78、1.44、1.30、0.76、1.00、0.88、0.58、0.87、1.12、0.59、0.51、0.63、0.80、0.87、1.01、0.80、0.73、0.70、1.06、0.80、0.79、0.67、1.10、0.60、1.02、0.65、0.52、0.85、0.38、0.81、0.38、0.60、0.63；组3的样本容量为63个，各实测值分别为0.38、0.48、0.41、0.43、0.46、0.37、0.34、0.46、0.33、0.42、0.46、0.44、0.31、0.43、0.37、0.30、0.38、0.44、0.42、0.37、0.39、0.42、0.41、0.41、0.41、0.42、0.45、0.34、0.41、0.39、0.39、0.42、0.36、0.35、0.42、0.40、0.49、0.43、0.41、0.41、0.38、0.41、0.38、0.52、0.39、0.44、0.42、0.37、0.39、0.43、0.42、0.44、0.51、0.48、0.44、0.39、0.52、0.51、0.49、0.43、0.42、0.58、0.51。几种方法的计算结果见表2。由表2可以看出，本文方法计算结果介于真实参数区间和其他2种方法的计算结果之间。

刘恒等[10]指出，对于小样本区间估计的优劣应该以区间位置和区间宽度来衡量，区间位置由区间界限表征，区间宽度由区间上下界差的绝对值表征，且区间宽度越小，表明估计方法越有效。按照这2项指标的定义，本文方法估计出来的区间在各种分布类型以及样本数量下显然优于3σ法以及考虑偏度的分布区间修正法。结合岩土工程中的实际情况得出的估计区间应该包含实测岩土参数分布区间[xmin，xmax]。本文改进方法结合该要求对原有的灰自助法进行了一定的改进，通过对灰色模型的预测步长进行调整，避免了原有灰色自助法得出的估计区间不满足岩土工程要求的不足，该方法的建立不借助于统计理论，理论上能适应各种分布类型的数据。

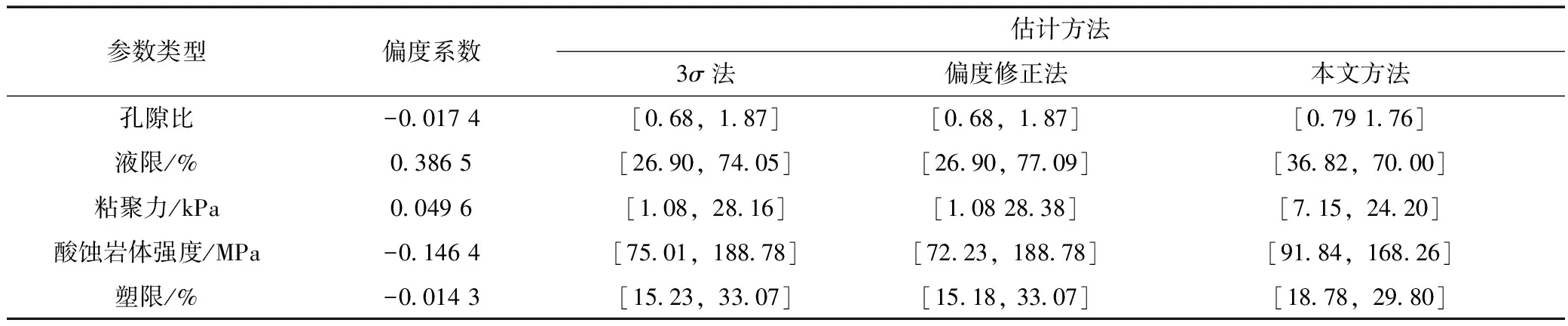
表1 计算结果

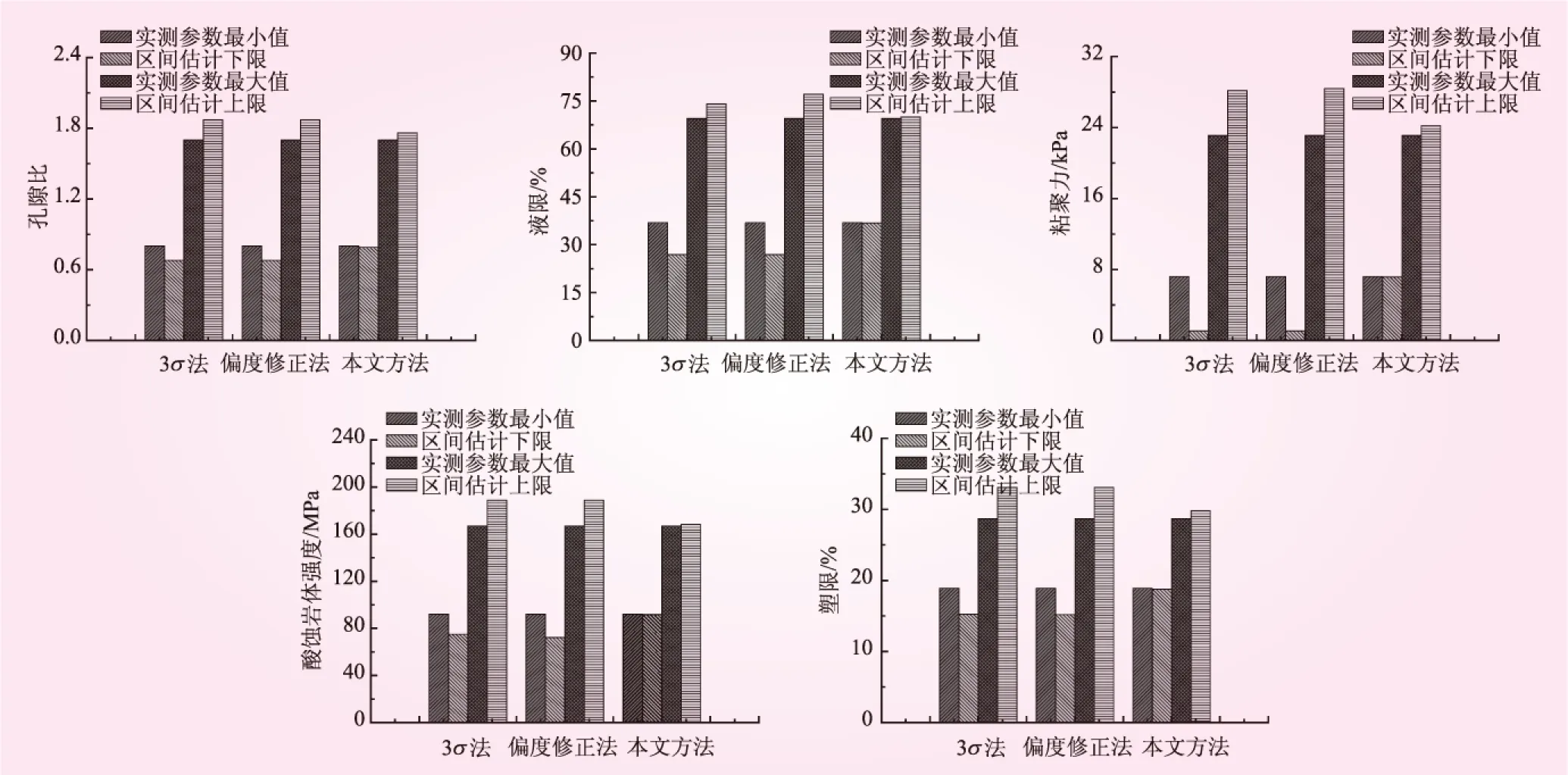
图1 计算结果对比

表2 计算结果

4 结 语

通过研究比较现有的多种小样本岩土参数区间估计方法，指出已有方法存在的不足，并提出了一种适用于小样本岩土参数区间估计的改进灰自助法，得出以下结论：

(1)在现有岩土参数区间估计方法中，3σ法通常只适用于正态分布情形，虽然考虑偏度的分布区间修正法对该方法进行了一定改进，但仍然更适用于正态分布情况，且多数情况下，这2种方法估计区间很接近。

(2)结合岩土工程的实际要求，即估计区间应该包含实测岩土参数分布区间[xmin，xmax]，对灰自助法中的灰色预测步长自动调整，从而避免估计区间不包含实测岩土参数分布区间[xmin，xmax]的不足。

(3)从文中算例可以看出，无论是在何种分布以及样本数量下，改进方法估计的区间始终优于3σ法以及考虑偏度的分布区间修正法。

[1]宫凤强, 黄天朗, 李夕兵. 岩土抗剪强度参数的最优概率分布函数推断方法[J]. 岩土工程学报, 2016, 38(z2)： 204- 209.

[2]宫凤强, 黄天朗, 李夕兵. 岩土参数最优概率分布推断方法及判别准则的研究[J]. 岩石力学与工程学报, 2016, 35(12)： 2452- 2460．

[3]宫凤强, 侯尚骞, 李夕兵. 岩土参数截尾分布的正态信息扩散推断方法[J]. 武汉大学学报： 工学版, 2016, 49(5)： 661- 673.

[4]孟庆山, 雷学文. 土工参数的统计方法及其工程应用[J]. 武汉冶金科技大学学报, 1999, 22(4)： 414- 417.

[5]姜立春, 杜卫卫. 受酸腐蚀岩体强度分布特征研究[J]. 昆明理工大学学报： 理工版, 2010, 35(4)： 6- 10．

[6]宫凤强, 黄天朗, 李夕兵. 岩土参数最优概率分布推断方法及判别准则的研究[J]. 岩石力学与工程学报, 2016, 35(12)： 2452- 2460．

[7]骆飞, 罗 强, 蒋良潍, 等. 小样本岩土参数的Bootstrap估计及边坡稳定分析[J]. 岩石力学与工程学报, 2017, 36(2)： 370- 379．

[8]刘义, 王国玉, 柯宏发.一种基于灰色距离测度的小样本数据区间估计方法[J]. 系统工程与电子技术, 2008, 30(1)： 116- 119．

[9]沈展鹏, 肖世富, 刘信恩, 等. 基于小样本信息的区间边界估计方法研究[J]. 应用力学学报, 2012, 29(6)： 692- 698．

[10]刘恒, 梅卫, 单甘霖. 小样本数据的三种区间估计方法性能分析[J]. 系统工程与电子技术, 2014, 36(10)： 1929- 1933．

(责任编辑 杨 健)

Discussion on Interval Estimation Method for Small Sample Parameters of Rock and Soil

LI Huayun1,2, FAN Honghai3, HU Duan4
(1. School of Architecture and Civil Engineering, Xihua University, Chengdu 610039, Sichuan, China;2. Key Laboratory of Green Building and Energy Saving, Xihua University, Chengdu 610039, Sichuan, China;3. Chinese Harbour Engineering, Beijing 100027, China; 4. Key Laboratory of Transportation Tunnel Engineering of Ministry of Education, Southwest Jiaotong University, Chengdu 610031, Sichuan, China)

The calculation of the distribution range of geotechnical parameters is a fundamental work in reliability analysis method. In actual project, as the number of samples is limited, the geotechnical parameters are mostly small sample. By comparing existing geotechnical parameter interval estimation methods of small sample (3σlaws, considering of skewness distribution range correction method and non-parametric Bootstrap method), the application and the deficiencies of above three methods is discussed. By combining the characteristics of interval estimation of geotechnical parameters, an improved gray self-help method is proposed for interval estimation of geotechnical parameters. The results show that the improved method is superior to existing method by comparing the distributions of different parameters and the number of samples．

geotechnical engineering; small sample; parameter; interval estimation

2017- 05- 31

国家青年科学基金项目(51608450)；西华大学绿色建筑与节能重点实验室开放基金项目(szjj2015- 075)

李化云(1982—)，男，江西吉安人，讲师，博士，主要从事岩土及地下工程研究．

TU43

A

0559- 9342(2017)08- 0044- 04