基于属性区间识别模型的边坡稳定性研究
王 艳,李绍红,尹维大,高延超
(1.成都理工大学,四川成都610059;2.中国地质调查局成都地质调查中心,四川成都610081)
基于属性区间识别模型的边坡稳定性研究
王 艳1,李绍红1,尹维大1,高延超2
(1.成都理工大学,四川成都610059;2.中国地质调查局成都地质调查中心,四川成都610081)
为快速准确地识别边坡的稳定性,从多因素综合评价角度,提出了一种基于属性区间识别的边坡稳定性评价的新模型。在建立边坡稳定性评价体系的基础之上,采用AHP法和熵权法分别计算指标的主观权重和客观权重,采用最优离差组合赋权法计算各因素指标权重,并通过属性区间识别技术判别边坡的稳定性。算例表明,该模型能够获得与可拓方法、灰色理论一致的评价结果,可作为边坡稳定性评价的补充方法。
边坡工程;稳定性评价;属性区间识别;熵权法;最优组合赋权法
0 引 言
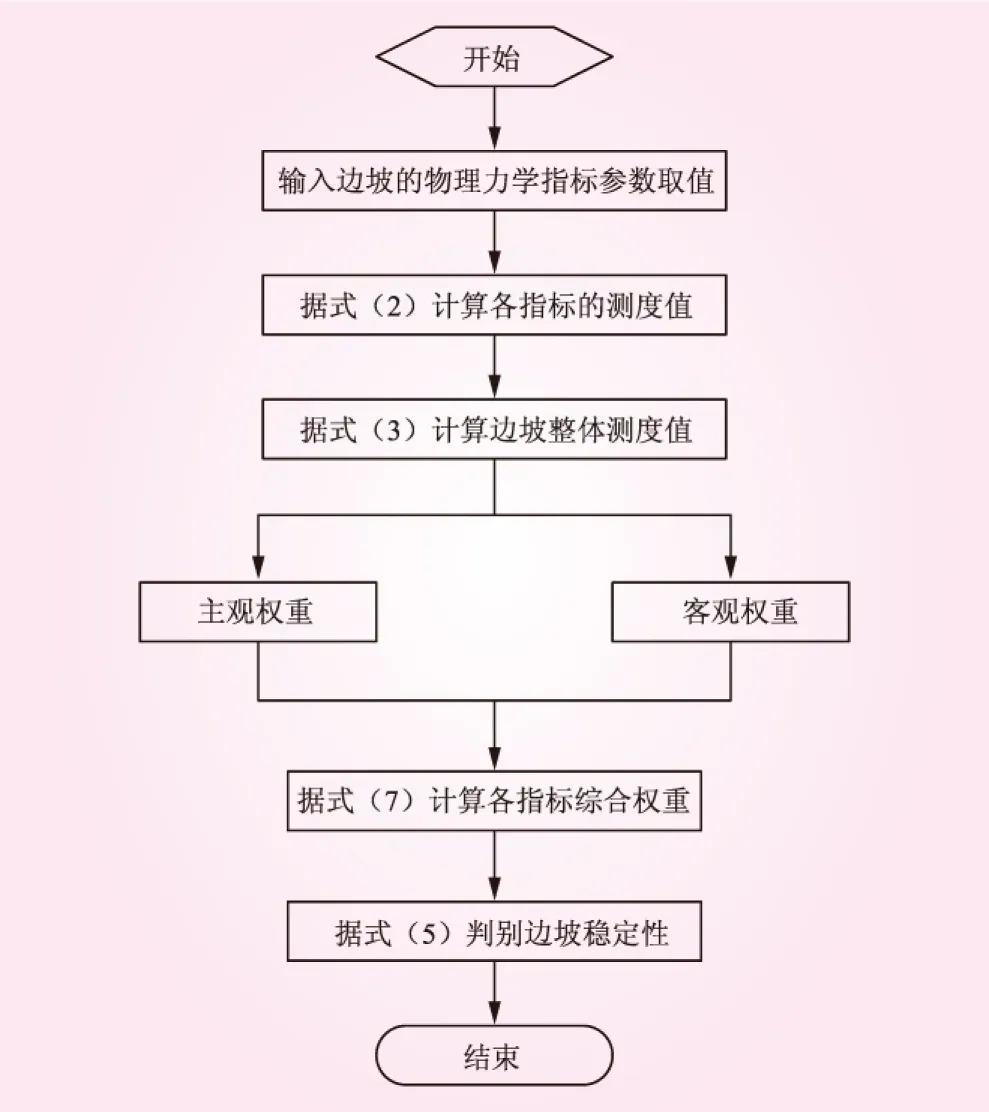
目前,边坡稳定性评价方法有物理力学方法[1-2](极限平衡法、极限分析法、有限元法等)和数学方法(多指标评价模型法、可靠度方法等),各种方法各有其优势。其中,数学方法中的多指标评价模型法具有简单适用的优点,在边坡工程中得到了一定应用,且应用于解决岩爆预测[3]、围岩稳定性评估[4]等问题。兰海涛等[5]将广义回归神经网络用于估计边坡的稳定性,以边坡几何因素和物理力学参数作为模型输入,构建了边坡稳定性估计的黑箱模型,实例计算发现应用效果较好;刘磊磊等[6]将TOPSIS模型用于边坡稳定性评价,通过建立边坡稳定性评价体系,结合AHP定权,可快速准确地识别边坡的稳定性;丁丽宏等[7]通过修改标度改进了标准AHP,并结合灰色理论完成了边坡稳定性评价。上述方法的引入,进一步丰富和发展了边坡稳定性评价体系。李群等[8]通过属性数学相关理论,提出更适用于区间评价问题的属性区间模型,与其他评价模型如灰色模型、可拓学模型相比,该模型在求解有序分割问题上具有较大的优势。鉴于该模型的优势,徐飞等将其用于围岩稳定性评价之中,求解结果显示该模型是有效实用的;邹强等[9]将其用于溃坝风险评估之中,也取得了满意的结果。但从以上研究中发现,采用该模型求解实际问题时,权重的选择对评价结果的影响较大。徐飞等仅通过PP方法求取其权重,缺乏合理性。
本文结合属性区间模型的优势,将其用于研究边坡的稳定性,并重点对权重计算方法进行了讨论,以期能为边坡稳定性评价提供一种简洁适用的方法。
1 属性区间识别模型
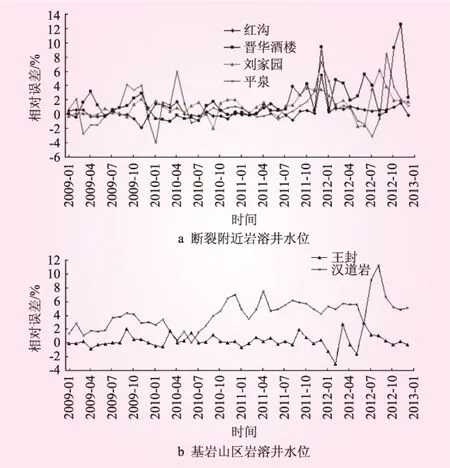
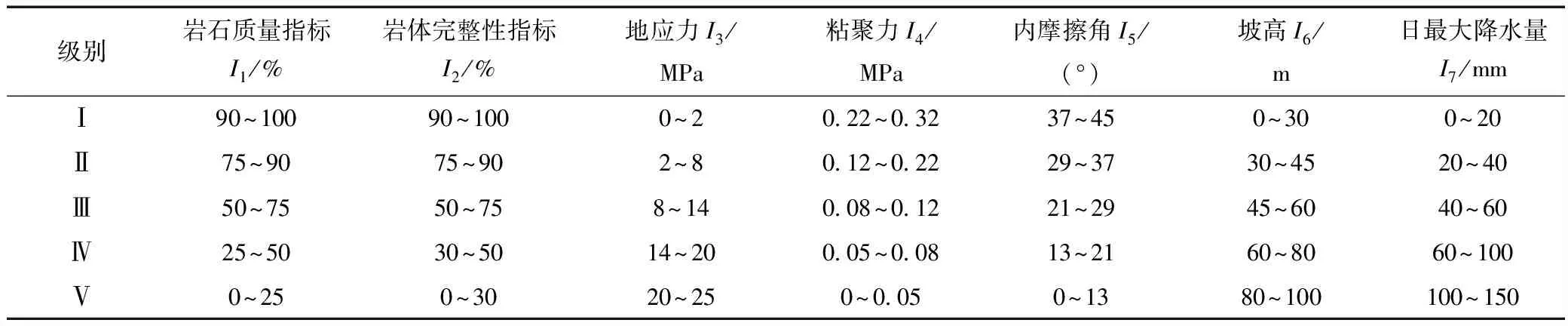
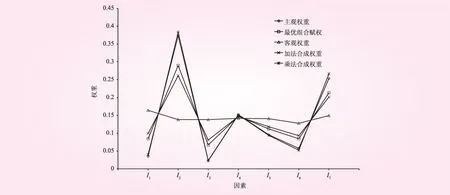
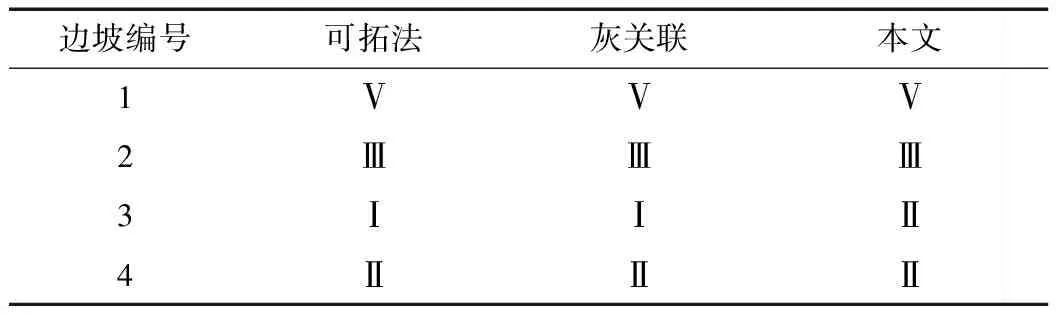
定义X为研究对象的全体取值空间,在X上存在n个样本,每个样本存在m个评价指标,并假定F为X上的某类属性空间,(C1,C2,…,CK)为X上的一个有序分割类。本文中,将F分为5类,且满足C1 (1) 式中,ail、bil(1≤i≤m,1≤l≤K)表示指标i在l类上的区间左右端点取值,且满足单调递增或单调递减原则。 1.1 单指标属性测度区间计算 (2) 按式(2)计算出单指标的属性测度区间后,按下式计算综合属性测度,即 (3) 式中,a为属性测度区间均化系数,一般取为0.5。 1.2 样本类别识别 设每个指标所占权重为wi(1≤i≤m),则样本i属于类别p的属性测度为 (4) 计算得到uip后,按下式判断所属稳定性类别pi,即 (5) 式中,λ表示置信度(本文取为0.6)。对于式(5),其计算方式是不断增加p取值,直到满足为止,此时的p值就是边坡稳定性所属的类别。依据属性识别准则,可以计算出样本i的评分值qi,即 (6) 依据qi的大小,即可对待测边坡样本进行排序。 1.3 权值计算 式(4)中权重wi可按照最优离差组合赋权法获得。首先计算其主观权重和客观权重,主观权重采用AHP法获取,客观权通过熵权法获取。熵权法计算步骤可参考罗军刚等[10-13]的研究。设由AHP法计算出的主观权重为pj(本文中j=1,2,…,7),由熵权法得到的客观权重记为qj,并记wj=x1pj+x2qj。其中,x1、x2表示将主观权重和客观权重进行组合的线性组合系数,且满足 (7) 由线性加权法可知,根据组合权重w计算出的第i个评价对象的综合评价值Di可写为 (8) 式中,rij表示第i个待评价边坡的第j个指标值。 (9) 计算出式(7)的解后,对其进行归一化处理得到x1′、x2′,从而得出最终的组合权重wj,即 wj=x1′pj+x2′qj (10) 为了直观地展现本文采用方法的步骤,图1给出了相应的流程图。 2.1 评价体系的建立 按照评价指标选取相关原则(全面性、代表性、可测量性),参考丁丽宏等研究成果,确定岩石质量指标I1、岩体完整性指标I2、地应力I3、粘聚力I4、内摩擦角I5、坡高I6、日最大降水量I7等7个指标对边坡稳定性进行评价。边坡稳定性分级标准见表1。 表1 边坡稳定性分级标准 表2 边坡相关参数 图1 边坡稳定性评价流程 2.2 工程概况 1号边坡为地处丘陵斜坡地貌区的渝黔高速公路某岩质边坡,坡高约46 m,坡角约64°。边坡岩体为上部砂岩、下部泥岩互层,岩层倾向约55°,倾角约23°[12]。由钻探结果可知,该坡体砂岩与泥岩结合性较差,软弱层与边坡倾向一致,对边坡的稳定性构成了一定的威胁。该坡体岩体质量一般,节理裂隙不发育,坡体所处地区降水量大,对边坡稳定极不利。2、3、4号边坡位于首钢某矿区,地处华北地台北缘,燕山沉降带中部,迁安隆起西缘的褶皱带,南部杏山复向斜构造中。矿区所在范围内出露地层主要以太古界迁西群三屯营组变质岩为主,矿床主体为F9断层破坏的向斜构造。向斜北部仰起端和西翼受旋钮断层F9的破坏,导致向斜形态不完整[7]。矿区所在区域年降水量丰富,年平均降雨量为756 mm,日最大降水量为344.8 mm。边坡相关参数见表2。 2.3 模型应用及分析 结合式(1)和表1,构造出边坡稳定性分类标准判断矩阵如下 C1C2C3C4C5 图2 计算结果对比 按照本文的最优组合权值计算方法计算各个指标的权重。图2给出了单一的AHP定权法(主观权重)、熵权(客观权重)以及平均线性加法合成法、乘法合成法、最优组合赋权方法等5种不同的组合权重计算方法的结果。平均线性加法合成法、乘法合成法、最优组合赋权法简要数学描述见表3。从图2可知,最优组合赋权法明显优于其他2种合成方法。其中,乘法合成法几乎没有利用到客观权重所提供的信息,其可信度最差;而平均线性加权法将主客观权重视为同等重要,也存在一定的不足。 表3 简要数学描述 按照文中的计算方法,最终计算得到综合属性测度区间如下 C1C2C3C4C5 按照式(5)即可以判断边坡稳定性的级别,取置信区间为0.6,4个边坡的稳定性分级见表4。由表4可知,本文所提出的模型在对1、2、4号边坡进行评价时,得到的结果和灰关联评估、可拓法是一致的。对3号边坡的评估值和其他2种方法并不一致,原因之一在于灰关联评估、可拓法都是单纯以层次分析法计算权值,带有一定的主观性,而本文模型通过融合主观权值和客观权值,获得的权值更为可靠。从3号边坡的实测数据可知,其在Ⅰ级区间内有2个指标,在Ⅱ级区间内有3个指标,在Ⅲ级区间内1个,在Ⅴ级区间内1个,将其总体稳定性归于Ⅰ级是不合理的。相比之下,本文的方法评估所得到的结论则显得更为合理。根据式(6),可以进一步将各个边坡的稳定性进行评分排序,排序结果为1>2>4>3,即1号边坡的稳定性最差,2号次之,4号再次之,3号最好。 表4 评价结果 本文从多因素综合评价角度,提出了一种基于属性区间识别的边坡稳定性评价的新模型,并应用于边坡稳定性评价中,得出以下结论: (1)权重对评价结果的影响是明显的,通过最优离差组合赋权能够综合主、客观权重,是一种实用且有效的权重计算方法。 (2)算例表明,本文方法能够取得和可拓学方法、灰关联方法较为一致的结果。 (3)本文选择的指标因素仍然不够完善,在今后应用中,可考虑增加一些其他指标因素。 [1]WANG H B, XU W Y, XU R C. Slope stability evaluation using back propagation neural networks[J]. Engineering Geology, 2005, 80(3): 302- 315. [2]CHOOBBASTI A J, FARROKHZAD F, BARARI A. Prediction of slope stability using artificial neural network (case study: Noabad, Mazandaran, Iran)[J]. Arabian Journal of Geosciences, 2009, 2(4): 311- 319. [3]龚剑, 胡乃联, 崔翔, 等. 基于AHP-TOPSIS评判模型的岩爆倾向性预测[J]. 岩石力学与工程学报, 2014, 33(7): 1442- 1448. [4]徐飞, 王珂, 刘造保. 围岩稳定性评价的投影寻踪权重-属性区间识别模型[J]. 岩土力学, 2010, 31(8): 2587- 2592. [5]兰海涛, 李谦, 韩春雨. 基于广义回归神经网络的边坡稳定性评价[J]. 岩土力学, 2009, 30(11): 3460- 3463. [6]刘磊磊, 绍和, 刘利茂. 岩质边坡稳定性分级的AHP-理想点模型及应用[J]. 中南大学学报: 自然科学版, 2014, 45(10): 3499- 3504. [7]丁丽宏. 基于改进的灰关联分析和层次分析法的边坡稳定性研究[J]. 岩土力学, 2011, 32(11): 3437- 3441. [8]李群, 宁利. 属性区间识别理论模型研究及其应用[J]. 数学的实践与认识, 2002, 32(1): 50- 54. [9]邹强, 周建中, 杨小玲, 等. 属性区间识别模型在溃坝后果综合评价中的应用[J]. 四川大学学报: 工程科学版, 2011, 43(2): 45- 50. [10]罗军刚, 解建仓, 阮本清. 基于熵权的水资源短缺风险模糊综合评价模型及应用[J]. 水利学报, 2008, 39(9): 1092- 1097. [11]张以晨, 佴磊, 孟凡奇, 等. 基于最优组合赋权理论的可拓学评价模型的应用[J]. 吉林大学学报: 地球科学版, 2011, 41(4): 1110- 1115. [12]李克钢, 许江, 李树春, 等. 基于可拓理论的边坡稳定性评价研究[J]. 重庆建筑大学学报, 2007, 29(4): 75- 78. [13]李军霞, 王常明, 王钢城. 基于组合赋权-未确知测度理论的滑坡危险性评价[J]. 岩土力学, 2013, 34(2): 468- 474. (责任编辑 杨 健) Slope Stability Evaluation Based on Attribute Interval Recognition Model WANG Yan1, LI Shaohong1, YIN Weida1, GAO Yanchao2 For identifying slope stability quickly and accurately, a new model for slope stability evaluation based on attribute interval recognition is put forward from the perspective of multi-factor comprehensive evaluation. After establishing slope stability evaluation system, the AHP method and entropy weight method are firstly used to calculate the subjective weights and objective weights of index parameters respectively, and then the final weights are obtained by using optimal combination empowerment deviation method, and finally the slope stability is identified by attribute interval recognition criterion. The engineering example calculations show that the results of new model can achieve same evaluation results with extension model and grey theory. The new method can be used as a supplement in slope stability evaluation. slope engineering; stability evaluation; attribute interval recognition; entropy; combination weighting combined method 图5 相对误差 四川省国土资源厅联合科技攻关项目(0773-1641 GNSC01693) 王艳(1992—),女,吉林长春人,硕士研究生,主要研究方向为水文地质与工程地质;高延超(通讯作者). TU457 A 0559- 9342(2017)08- 0039- 05 2017- 04- 19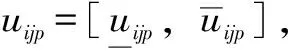

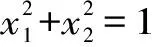
2 边坡稳定性评价



3 结 语
(1. Chengdu University of Technology, Chengdu 610059, Sichuan, China;2. Chengdu Center of China Geological Survey, Chengdu 610081, Sichuan, China)