N波诱发的瞬变港湾振荡的数值研究

高俊亮，郑子波，嵇春艳，刘珍

(1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003； 2.江苏科技大学 江苏省船舶先进设计制造技术重点实验室，江苏 镇江 212003； 3.大连理工大学 船舶工程学院，辽宁 大连 116024)

N波诱发的瞬变港湾振荡的数值研究

高俊亮1,2，郑子波3，嵇春艳1，刘珍1

(1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003； 2.江苏科技大学 江苏省船舶先进设计制造技术重点实验室，江苏 镇江 212003； 3.大连理工大学 船舶工程学院，辽宁 大连 116024)

为了研究海啸波诱发的瞬变港湾振荡问题，本文采用一组完全非线性Boussinesq模型，模拟了由波峰在前和波谷在前的两种类型的等边N波入射诱发的狭长矩形港内的瞬变港湾振荡现象。基于正交模态分解法，定量分离了港内不同共振模态的响应幅值，并系统研究了入射N波类型和入射波波幅对港内相对波能分布的影响。研究表明：在本文所研究的特定港口和入射波波幅范围内，当入射波波幅较小时，以上两种类型N波诱发的港内相对波能分布几乎完全相同，并且波能几乎都集中在最低的几个共振模态上。随着入射波波幅的增大，分布于更高模态上的波能的比重增加，港内波能的分布趋于均匀，并且占有最大波能的共振模态逐渐由较低的模态向较高的模态转移。相比于波峰在前的等边N波，波谷在前的等边N波诱发的港内波能分布得更加均匀。

海岸工程； 港湾振荡； 矩形港口； Boussinesq模型； N波； 正交模态分解法； 波能分布； 波幅；瞬变

港湾振荡是指当近岸海域的低频波浪传播到港湾内，如果其频率和港湾的本征频率相一致，那么就会激起港湾内剧烈的水体共振的现象。港湾振荡可以诱发港内泊船的剧烈运动，显著影响系泊安全和货物的装卸[1]。海啸波已被证实能够诱发显著的港湾振荡[2]，且由其诱发的瞬变港湾振荡往往具有破坏性[3]。

以往对于港湾振荡的研究主要集中于由平稳的波浪所诱发的稳态振荡[4-5]，瞬变港湾振荡的研究工作起步较晚且研究的也较少。使用理论和实验方法，Lepelletier于20世纪80年代开始了对海啸等非线性瞬变长波诱发的瞬变共振的研究[6]。Dong 等使用物理模型实验并结合数值模拟对由滑坡产生的冲击波在矩形港内的共振反应进行了研究[7]。Wang 等基于Boussinesq 模型对一个具有常底坡的矩形港内由水底运动诱发的瞬变港湾振荡进行了系统地研究[8]。近期，作者使用Boussinesq 模型模拟了孤立波入射诱发的狭长型港湾内的瞬变振荡现象，并采用正交模态分解法系统研究了港口底坡和入射孤立波波高的变化对港内相对波能密度分布的影响[9]。

目前，海啸诱发的瞬变共振研究多限于使用孤立波来进行研究[7, 9]，但从很多地震海啸的实际观测中发现多数海啸波是由一个大波峰和一个大波谷组成，形状像“N”，这类海啸波被称为N波，且根据波形的不同，N波可进一步分为波峰在前的N波、波谷在前的N波、等边N波和一般化的N波[10-11]。

本文使用FUNWAVE-TVD模型和正交模态分解法进行了数值实验。通过对波峰在前和波谷在前的两种类型的等边N波诱发的狭长矩形港内的瞬变港湾振荡现象进行的数值模拟，验证了正交模态分解法的准确性。研究了入射N波形式和入射波波幅对港内相对波能分布的影响。

1 数值模型和分析方法

1.1 FUNWAVE-TVD模型

Boussinesq模型近些年来已被广泛地应用于模拟波浪在近岸的传播过程。它可以精确地模拟波浪的色散性、非线性、浅水变形、破碎和波成流等一系列的现象[12]。本文使用FUNWAVE-TVD模型[13]来实施数值实验。该数值模型是以Chen[14]的完全非线性Boussineq方程为基础开发的。Kennedy等的动参考层技术被进一步应用于控制方程中，使得模型能够更好地模拟冲流带和沿海洪水的动边界现象[15]。该模型使用一个非常均衡的守恒形式来组织控制方程，并使用一个高阶激波捕捉全变差下降格式来对控制方程进行数值离散。该技术允许模型能够不依赖于经验公式而很好地模拟波浪破碎和相关的波能耗散现象。此外，该模型的时间离散使用保持强稳定性的三阶Runge-Kutta方法，使得模型具备了自适应时间步长的功能。此外，模型使用了具有非阻隔通信的消息传递接口技术，使其可进行并行计算，显著提高了数值计算的效率。FUNWAVE-TVD模型已被证实能够很好模拟包括波浪浅水变形、反射、衍射、破碎、在岸滩上的爬高、下冲和波成流等一系列的近岸波浪水动力现象[13]。

1.2 改进的模态分析法

正交模态分解法由Sobey[16]首先提出，该方法可用于计算港口本征频率、共振模态形状和定量分离由风暴潮和海啸诱发的瞬变港湾振荡的各共振模态的响应幅值。该方法包含两个计算步骤：1) 以线性长波方程为起点，把控制方程转化为一个Sturm-Liouville问题，并最终离散为矩阵方程，矩阵方程的特征值和特征向量即为港口的本征频率和对应的共振模态形状；2) 通过一个多维优化问题对由风暴潮和海啸诱发的瞬变港湾振荡的各共振模态的响应幅值进行分离，第一步中计算得到的本征频率和共振模态形状将作为已知参数用于第二步的计算中。近期，Gao等[17]使用镜像原理对正交模态分解法进行了改进，显著提高了其预测港口本征频率和共振模态形状的精度，并用此方法研究了孤立波入射条件下港内发生瞬变共振时港口底坡和入射孤立波波高的变化对港内相对波能密度分布的影响[9]。本文首次将文献[17]中改进后的正交模态分解法用于N波诱发的瞬变港湾共振问题的研究，定量分离了港内各共振模态的响应幅值，并进一步系统研究了入射N波类型和入射波波幅的变化对于港内相对波能分布的影响。

2 数值实验布置

图1展示了本文所用港口的平面布置情况。港口长度为L=1 000 m，宽度为W=20 m。港内外水深均为h=10 m。海岸线和港内边墙均设置为全反射直墙。笛卡尔坐标系统(o,x,y,z)的原点取在静水面，z轴垂直向上为正。

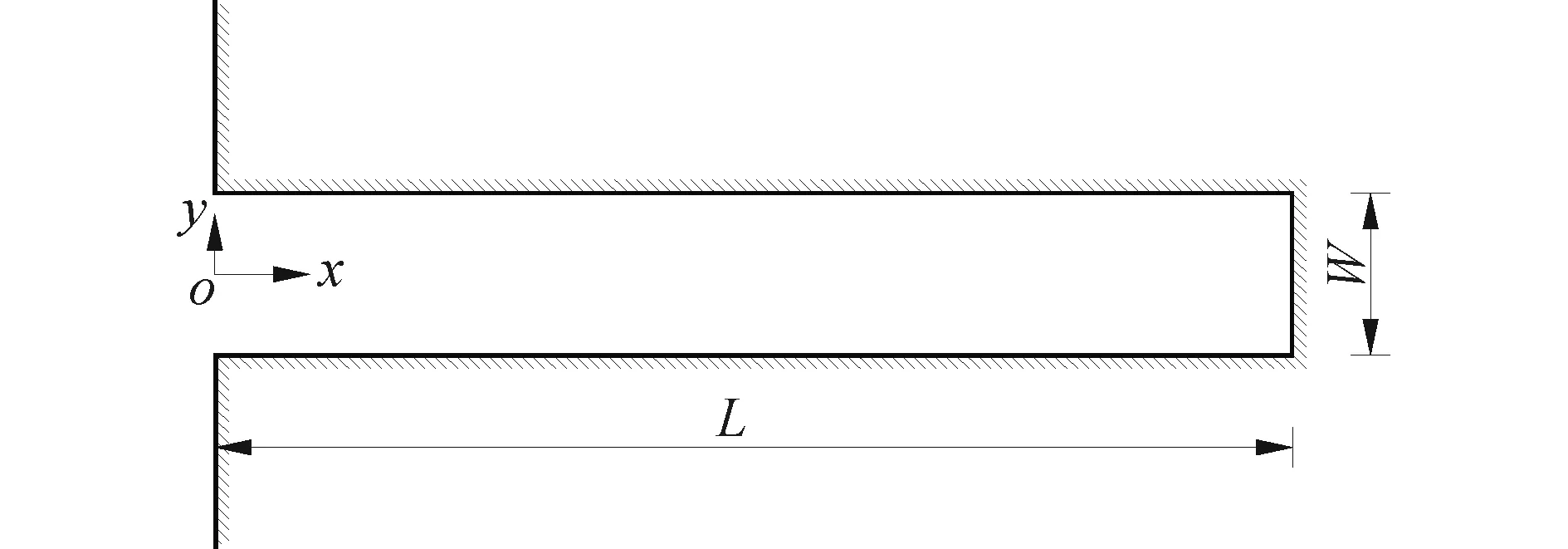
图1 港口平面概图Fig.1 Plan view of the harbor

本文中，外海入射波采用Tadepalli和Synolakis[10-11]提出的波峰在前和波谷在前的两种类型的等边N波，它们的表达式为

(1)

其中

(2)

式中：η表示自由波面，A0表示入射波波幅，x0表示初始入射N波的中心位置，方程等号右端的正号对应于波峰在前的等边N波，负号对应于波谷在前的等边N波。位于控制方程速度参考面处的初始水质点速度可用如下的线性表达式表示：

(3)

为了研究不同的入射N波类型对于瞬变港湾振荡的影响，本文设计了两组系列实验，即A组和B组。在A组中，外海初始入射波均为波峰在前的等边N波；而在B组中，外海初始入射波均采用波谷在前的等边N波。同时，为了研究入射N波波幅对于瞬变港湾振荡的影响，在这两组系列实验中，入射波波幅A0均从0.005 m逐渐增大到0.30 m。所有数值实验的波浪参数见表1。

表1 数值实验的入射波浪参数

Table 1 Incident wave parameters for the numerical experiments

实验系列组号A0/m实验系列组号A0/mA组A010005A02001A03005A04010A05015A06020A07025A08030B组B010005B02001B03005B04010B05015B06020B07025B08030

图2显示了入射波波幅A0为0.005 m和0.30 m时波峰在前和波谷在前的等边N波的波形图。如图所示，当入射波幅相同时，波峰在前和波谷在前的等边N波波形的相位相差了180°。图中的圆点表示对应的N波的“波前”。波前被定义为其所在处的自由波面ηf=±0.05A0。本文中，等边N波的波长L0被定义为波前和中心位置x0之间的两倍距离。当A0=0.005 m时，波长L0=1 703.6 m；而当A0=0.30 m时，波长显著减小为L0=220.0 m。

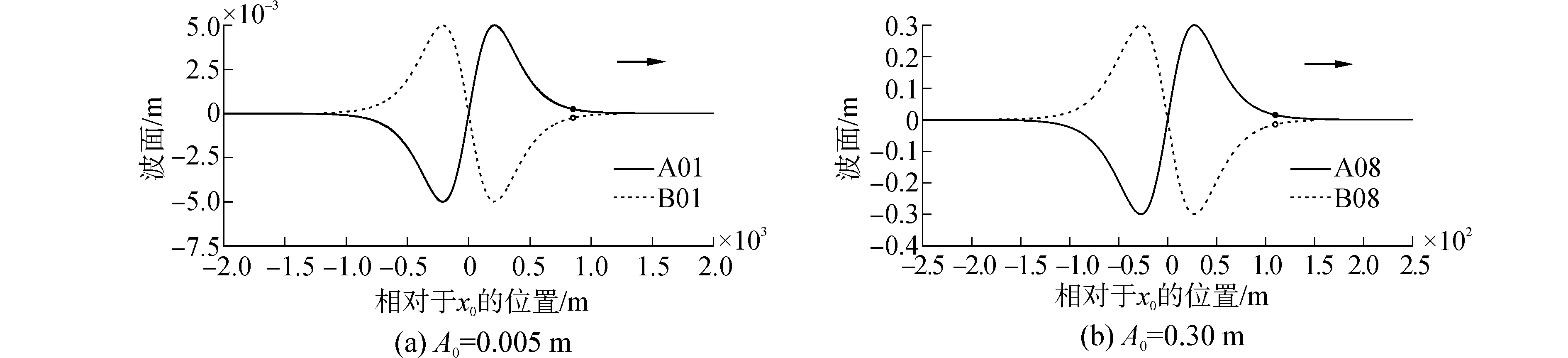
图2 波峰在前和波谷在前的等边N波的波形图Fig.2 Profiles of the isosceles leading-elevation N-waves and the isosceles leading-depression N-waves

图3为数值实验中所用的数值波浪水槽。数值波浪水槽尺寸为4 000 m×50 m。

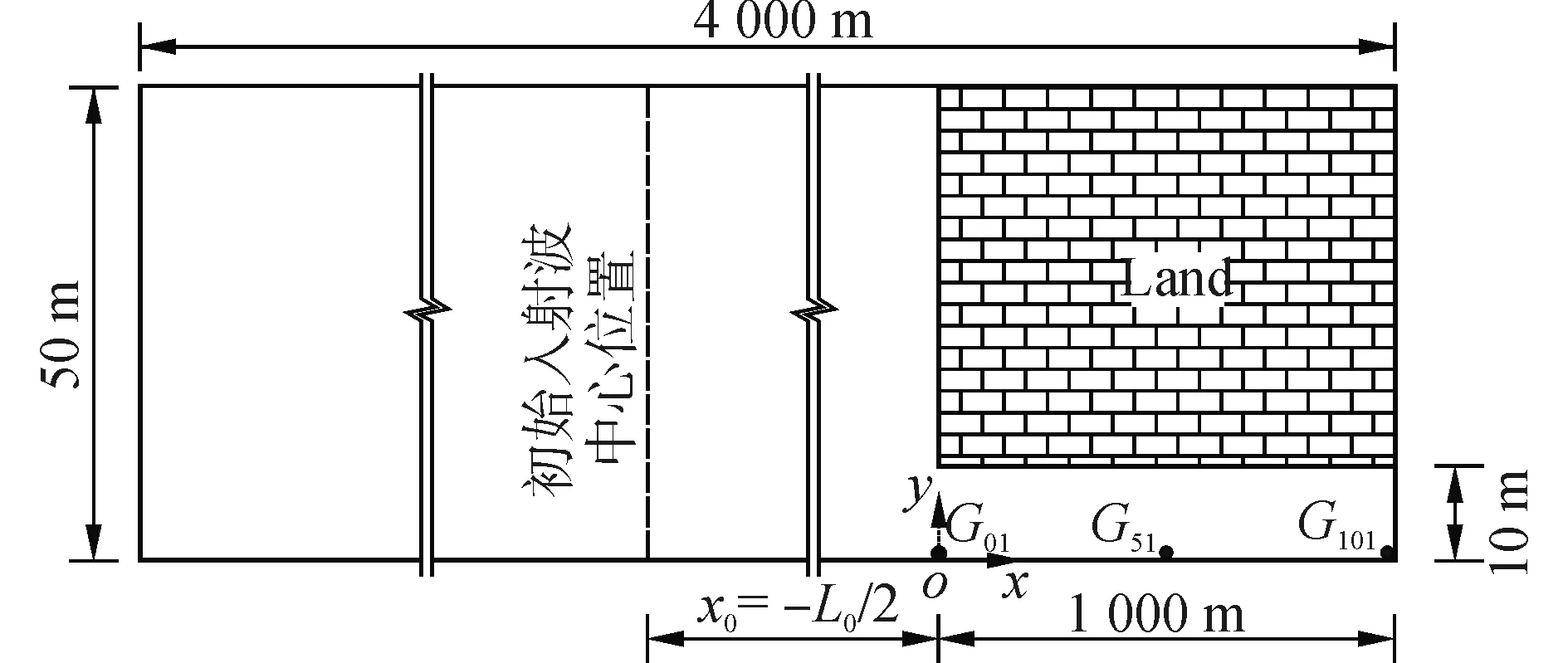
图3 数值波浪水槽概图Fig.3 Sketch of the numerical wave flume

因为图1所示港口关于x轴对称，为了节省计算网格和时间，仅模拟港口和外海的一半区域。港内等间距布置了101个测点(G01～G101)，相邻两个测点的间距为10 m。测点G01布置在港口口门处(x=0)，而测点G101布置在港口底墙处(x=1 000 m)；x和y方向网格尺寸均为Δx=Δy=1 m。网格节点和单元数分别为204 051和200 000个；所有边界均设置为全反射；作为初始条件，入射N波的波前均设置在港口门位置处；所有的数值实验均模拟到300 s。

3 模拟结果和港内波能分析

在正交模态分解法的使用过程中，需要预先指定所需考虑的共振模态数量M[16-17]。本文对于所有的数值实验均设置M=40。图4 显示了在实验A02 和B02 中使用FUNWAVE-TVD 模型模拟得到的自由波面和对应的使用正交模态分解法拟合得到的自由波面的比较。图中，Aus和Auf分别表示模拟和拟合得到的入射N波在港内的最大爬高值，而Ads和Adf分别表示模拟和拟合得到的入射N波在港内的最大下冲值。对这两个算例，拟合的自由波面和模拟的自由波面吻合得很好。对于实验A02，入射波波幅为A0=0.01 m，模拟的自由波面(图4(a))在位于x=1 000 m的港口底墙处、在t=147.6 s 的时刻出现了最大爬高值Aus=0.032 22 m；而在相同的位置和时刻，拟合的自由波面(图4(b))出现Auf=0.032 16 m的最大爬高值。类似地，模拟的自由波面在港口底墙处、t=178.7 s 时出现了最大下冲值Ads=0.033 19 m；而在相同的位置和时刻，拟合的自由波面也出现Adf=0.033 19 m的最大下冲值。对于实验B02，入射波波幅也为A0=0.01 m，模拟的自由波面(图4(c))在港口底墙处、t=148.0 s时出现了最大下冲值Ads=0.032 21 m，在t=177.8 s时出现了最大爬高值Aus=0.032 24 m；而在相同的位置和对应的时刻，拟合的自由波面(图4(d))分别出现了Adf=0.032 17 m和Auf=0.033 20 m的最大下冲值和最大爬高值。本文定义了正交模态分解法在各组数值实验中用于拟合由数值模拟得到的自由波面的数值拟合误差(NFE)：

(4)

图4 模拟的和拟合的自由表面比较Fig.4 Comparison of the simulated and the fitted free surfaces

该参数可以直观地反映正交模态分解法分离不同共振模态响应幅值的精确性。对于实验A02和B02，正交模态分解法的数值拟合误差分别为0.19%和0.12%。表2中呈现了所有数值实验中正交模态分解法的数值拟合误差。可以发现，所有实验的数值拟合误差均小于4.40%。这表明在所有的数值实验中，正交模态分解法分离得到的各共振模态的响应幅值是精确可靠的。

本文将各组数值实验中港内的各共振模态响应幅值与相应的入射波波幅的比值定义为各模态的相对幅值，即：

(5)

表2 正交模态分解法的数值拟合误差

Table 2 Numerical fitting errors (NFEs) of the normal mode decomposition method

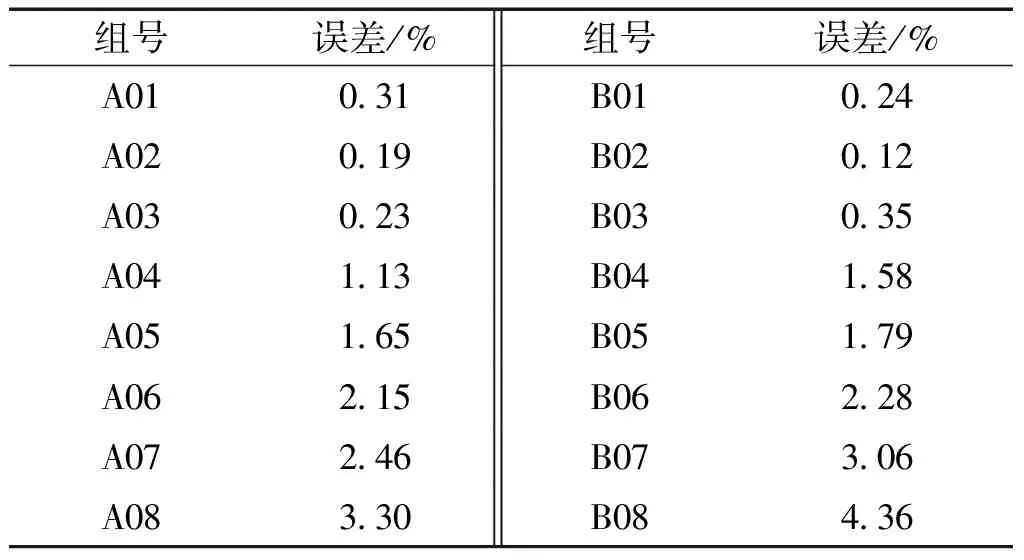
组号误差/%组号误差/%A01031B01024A02019B02012A03023B03035A04113B04158A05165B05179A06215B06228A07246B07306A08330B08436

图5显示了所有的数值实验中最低的40个共振模态的相对幅值分布。可以看出，相对幅值在各模态上的分布受入射N波波幅的影响很大。以A组为例(图5(a))。实验A01中，入射波波幅为A0=0.005 m，港内的波能主要集中在最低的四个模态上。随着入射波波幅的增大，分布于更高模态上的波能的比重逐渐增加，港内的波能分布逐渐趋于均匀。在实验A08 中，入射波波幅为A0=0.30 m，港内大部分的波能分布于更多的共振模态上(主要在最低的15个模态上)，港内波能分布趋于均匀。此外，在实验A01中占据最大相对波能的模态为第二模态，而随着入射波波幅的增大，占据最大相对波能的共振模态逐渐向较高的模态转移，在实验A08中具有最大相对波能的模态已转移到第七模态。对于B组(图5(b))，同样能够观察到类似的现象。随着入射波波幅的增加，港内波能向高模态转移且波能分布逐渐趋于均匀的原因可能与入射N波波长的减小有关。

图5 所有数值实验中港内相对幅值分布Fig.5 Relative amplitude distributions inside the harbor for all cases

为了比较不同入射N波类型对港内相对波能分布的影响，图6呈现了入射波波幅分别为0.005、0.15和0.30 m时波峰在前和波谷在前的两类等边N波诱发瞬变港湾振荡时港内相对幅值分布的比较。当A0=0.005 m时(图6(a))，两类不同的N波产生的港内相对幅值分布几乎完全相同。第二模态具有最大的相对幅值(相对波能)，随着共振模态的增大，相对幅值迅速地单调减小。当A0增大到0.15 m时(图6(b))，两类不同的N波产生的港内相对幅值分布出现了明显的不同。对于实验A05，港内最大相对幅值位于第六模态，为0.377；而在实验B05中，最大相对幅值位于第八模态，其值明显低于前者，仅为0.290，并且，总体来说，波能在港内的分布要比前者更为均匀。此外，还可以发现，在实验A05中，相对幅值分布除在第六模态存在最大值，在第十八模态还存在一个明显的次峰，而此现象在实验B05中并未出现。当A0进一步增大到0.30 m时(图6(c))，两类不同的N波产生的相对幅值分布的差别同样非常明显。在实验B08中，最大相对幅值仍然明显低于实验A08中的值，波能在港内的分布仍较实验A08中更为均匀。实验A08中相对幅值的次峰相比于实验A05中更加明显，而且实验B08中也出现了较为明显的次峰。

图6 不同入射N波类型产生的港内相对幅值分布的比较Fig.6 Comparison of the relative amplitude distributions excited by different types of incident N-waves

图7显示了在实验A01和B01中测点G101测得的自由波面时间序列和对应的小波谱。小波谱定性地表明了相对波能密度在时域和频域的分布。这两组实验中，虽然测点G101测得的自由波面时间序列相位相差了180°，但是它们对应的小波谱几乎是完全相同的，即表明港内相对波能分布情况几乎完全相同。小波谱表明第二模态占有最大的波能。尽管第一模态占有的波能也很显著，但是要明显低于第二模态。第三模态占有的波能要比前两个模态的波能小得多。这些现象和图6(a)中呈现的结果是一致的。

图8显示了在实验A08和B08中测点G101测得的自由波面时间序列和对应的小波谱。这两组实验中，测点G101处的自由波面时间序列和对应的小波谱均存在明显不同。在实验A08中，波浪在港内的最大的爬高值为0.582 9 m，而实验B08中，波浪最大爬高值显著大于前者，为1.059 m。对于波浪在港内的最大下冲值，在实验A08和B08中，分别为-0.627 9 m和-0.488 6 m。在实验A08中，小波谱显示最主要的波能分布在频率f=0.03 Hz附近，另外在f=0.09 Hz附近的波能也较为明显，虽然相比于f=0.03 Hz附近的波能要小得多。而在实验B08中，小波谱显示主要的波能分布在f=0.06 Hz附近，且相比于实验A08来说，港内波能在频域的分布也较为均匀。这些现象和图6(c)中呈现的结果是一致的。

图7 A0=0.005 m时，测点G101测得的自由波面时间序列和对应的小波谱Fig.7 Time series of the free surfaces at the gauge G101 and the corresponding wavelet spectra for A0=0.005 m

图8 A0=0.30 m时，测点G101测得的自由波面时间序列和对应的小波谱Fig.8 Time series of the free surfaces at the gauge G101 and the corresponding wavelet spectra for A0=0.30 m

为了进一步定量地表示港内相对波能在不同共振模态上分布的均匀程度，本文计算了各组实验中最低的40个共振模态的相对幅值分布的标准差系数：

(7)

其中：

标准差系数可以直观地反映各共振模态的相对幅值相对于它们的平均值的离散程度。显然，标准差系数越小，港内相对波能在各模态的分布越均匀；反之，标准差系数越大，港内相对波能在各模态的分布就越不均匀。图9 展示了所有数值实验中最低的40个共振模态的相对幅值分布的标准差系数CV值。从图中可以发现，当入射波波幅较小时，CV的值较大，并且A组和B组中相应的CV值差异很小。这表明在此条件下港内相对波能在不同模态上分布的均匀性较差，但是不同的入射N波形式对港内相对波能分布的影响很有限。当入射波波幅逐渐增大时，A组和B组中的CV值均单调减少，并且当入射波波幅一定时，B组中的CV值要明显小于A组中相应的CV值。这表明当入射波波幅逐渐增大时，港内的相对波能在各共振模态的分布逐渐趋于均匀，并且波谷在前的等边N波所产生的港内相对波能分布比波峰在前的等边N波所产生的港内相对波能分布要更为均匀。该图中所呈现的这些现象同图5～8中所呈现的现象是一致的。

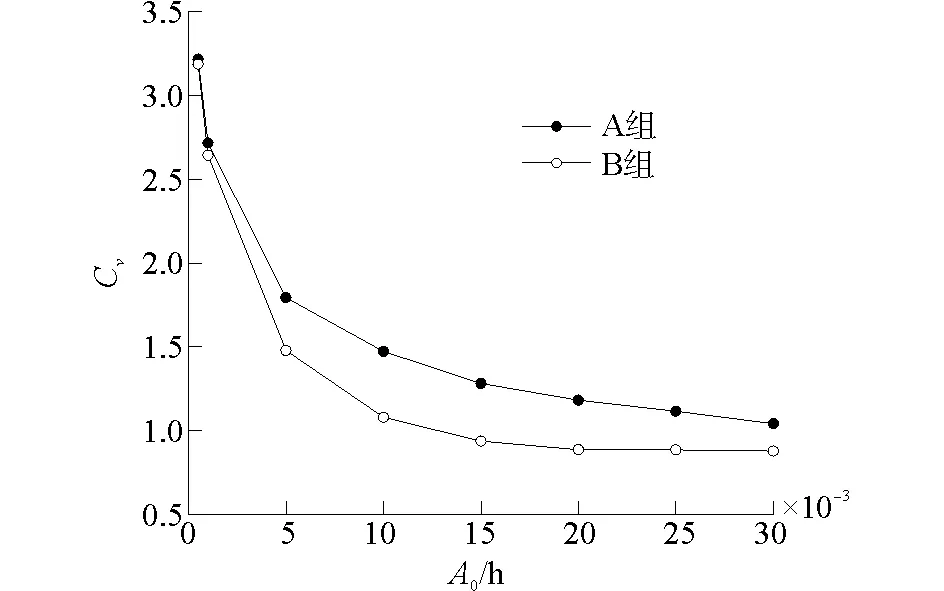
图9 所有数值实验中港内相对幅值分布的标准差系数CVFig.9 The CVvalues of the relative amplitude distributions inside the harbor for all cases

4 结论

1)当入射波波幅较小时，波峰在前和波谷在前的等边N波诱发的港内相对波能分布几乎完全相同，并且波能几乎都集中在最低的几个共振模态上，分布于更高模态上的波能极其有限。

2)随着入射波波幅的增大，分布于更高模态上的波能的比重增加，港内波能的分布趋于均匀，并且占有最大波能的共振模态逐渐由较低的模态向较高的模态转移。

3)相比于波峰在前的等边N波，波谷在前的等边N波诱发的港内波能分布得更加均匀。最后，需要说明的是，以上结论仅针对本文所使用的港口、入射等边N波类型和入射波波幅范围。

[2]KULIKOV E A, RABINOVICH A B, THOMSON R E, et al. The landslide tsunami of November 3, 1994, Skagway Harbor, Alaska [J]. Journal of geophysical research, 1996, 101(3): 6609-6615.

[3]PATTIARATCHI C B, WIJERATNE E M S. Tide gauge observations of 2004-2007 Indian Ocean tsunamis from Sri Lanka and Western Australia [J]. Pure and applied geophysics, 2009, 166(1): 233-258.

[4]GAO J, JI C, GAIDAI O, et al. Numerical study of infragravity waves amplification during harbor resonance [J]. Ocean engineering, 2016, 116: 90-100.

[5]DONG G, GAO J, MA X, et al. Numerical study of low-frequency waves during harbor resonance [J]. Ocean engineering, 2013, 68: 38-46.

[6]LEPELLETIER T G. Tsunamis-harbor oscillations induced by nonlinear transient long waves. Report No. KH-R-41[R]. Pasadena, California: W. M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, 1980.

[7]DONG G, WANG G, MA X, et al. Harbor resonance induced by subaerial landslide-generated impact waves [J]. Ocean engineering, 2010, 37(10): 927-934.

[8]WANG G, DONG G, PERLIN M, et al. Numerical investigation of oscillations within a harbor of constant slope induced by seafloor movements [J]. Ocean engineering, 2011, 38(17/18): 2151-2161.

[9]GAO J, MA X, DONG G, et al. Numerical study of transient harbor resonance induced by solitary waves [J]. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of engineering for the maritime environment, 2016, 230(1): 163-176.

[10]TADEPALLI S, SYNOLAKIS C E. The run-up of N-waves on sloping beaches [J]. Proceedings of the royal society london A: mathematical, physical & engineering sciences, 1994, 445: 99-112.

[11]TADEPALLI S, SYNOLAKIS C E. Model for the leading waves of tsunamis [J]. Physical review letters, 1996, 77(10): 2141-2144.

[12]KIRBY J T. Boussinesq models and applications to nearshore wave propagation, surfzone processes and wave-induced currents [J]. Elsevier oceanography series, 2003, 67: 1-41.

[13]SHI F, KIRBY J T, HARRIS J C, et al. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation [J]. Ocean modelling, 2012, 43-44: 36-51.

[14]CHEN Q. Fully nonlinear Boussinesq-type equations for waves and currents over porous beds [J]. Journal of engineering mechanics, 2006, 132(2): 220-230.

[15]KENNEDY A B, KIRBY J T, CHEN Q, et al. Boussinesq-type equations with improved nonlinear performance [J]. Wave motion, 2001, 33: 225-243.

[16]SOBEY R J. Normal mode decomposition for identification of storm tide and tsunami hazard [J]. Coastal engineering, 2006, 53: 289-301.

[17]GAO J, MA X, DONG G, et al. Improvements on the normal mode decomposition method used in harbor resonance [J]. Proceedings of the institution of mechanical engineers, part M: journal of engineering for the maritime environment, 2015, 229(4): 397-410.

本文引用格式：

高俊亮，郑子波，嵇春艳，等. N波诱发的瞬变港湾振荡的数值研究[J]. 哈尔滨工程大学学报， 2017， 38(8): 1203 -1209.

GAO Junliang, ZHENG Zibo, JI Chunyan, et al. Numerical study on transient harbor oscillations induced by n-waves[J]. Journal of Harbin Engineering University， 2017， 38(8): 1203-1209.

Numerical study on transient harbor oscillations induced by N-waves

GAO Junliang1,2, ZHENG Zibo3, JI Chunyan1, LIU Zhen1

(1.School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China; 2.Jiangsu Key Laboratory of Advanced Design and Manufacturing Technology for Ship, Jiangsu University of Science and Technology, Zhenjiang 212003, China; 3.School of Naval Architecture and Ocean Engineering, Dalian University of Technology, Dalian 116024, China)

To investigate transient oscillations excited by tsunamis, the transient oscillation phenomena inside a long and narrow rectangular harbor induced by isosceles leading-elevation N-waves and isosceles leading-depression N-waves were simulated with a fully nonlinear Boussinesq model. On the basis of a normal-mode decomposition method, the response amplitudes of different resonant modes of the harbor were decomposed quantitatively. Then, the effects of the amplitude and the type of the incident N-wave on the relative wave energy distribution inside the harbor were studied systematically. Results show that for the given harbor and the given range of the incident wave amplitude, when the incident wave amplitude is small, the relative wave energy distributions inside the harbor excited by the abovementioned two types of the N-waves are almost identical, and almost all the wave energy concentrates on the lowest few modes. With the increase in the incident wave amplitude, the proportion of the wave energy that is distributed over the higher modes increases, and the energy distribution inside the harbor becomes uniform. The resonant mode that possesses the highest wave energy shifts gradually from the lower mode to the higher one. Compared with the isosceles leading-elevation N-waves, the wave energy distribution inside the harbor excited by the isosceles leading-depression N-waves is more uniform.

coastal engineering; harbor oscillations; rectangular harbor; Boussinesq models; N-waves; normal mode decomposition method; wave energy distribution; wave amplitude; transient

2016-05-03.

日期：2017-04-27.

国家自然科学基金项目(51609108)；江苏科技大学江苏省船舶先进设计制造技术重点实验室开放研究基金项目(CJ1504).

高俊亮(1988-), 男, 讲师.

高俊亮，E-mail: gaojunliang880917@163.com.

10.11990/jheu.201605002

O353.2

A

1006-7043(2017)08-1203-07

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20170427.1413.062.html