水资源集对分析理论与应用研究进展

金菊良， 沈时兴， 潘争伟， 汪明武， 崔毅

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.合肥工业大学 水资源与环境系统工程研究所,安徽 合肥 230009; 3.安徽新华学院 土木与环境工程学院,安徽 合肥 230088; 4.天津大学 水利工程仿真与安全国家重点实验室,天津 300072)

水资源集对分析理论与应用研究进展

金菊良1,2， 沈时兴1,2， 潘争伟3， 汪明武1,2， 崔毅4

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.合肥工业大学 水资源与环境系统工程研究所,安徽 合肥 230009; 3.安徽新华学院 土木与环境工程学院,安徽 合肥 230088; 4.天津大学 水利工程仿真与安全国家重点实验室,天津 300072)

集对分析是利用结构式的联系数描述和处理系统不确定性问题的一类智能计算的新理论和新方法，基于处理不确定性问题的显著特点，开始被广泛应用于许多学科领域。水资源系统包含了随机性、模糊性等多种不确定性，集对分析是处理水资源确定不确定系统问题的理想的系统分析方法。从理论和应用研究方面对水资源集对分析进行了系统的综述，结果表明：联系数结构式是集对分析方法的重要创新，但其差异度系数的不确定性造成联系数运算的不确定性和复杂性，在一定程度上限制了集对分析理论体系的建立和发展，需要进一步加强水资源集对分析的理论基础研究，不断加深、拓宽和完善集对分析的理论体系。

水资源集对分析；联系数；差异度系数；水资源评价；水资源决策；水资源预测

事物的确定性与不确定性常常共处于一个统一体中，相互联系、相互影响、相互制约，并在一定条件下相互转化，从系统角度看，确定性与不确定性是一个确定不确定系统[1-6]。基于此，中国学者赵克勤于1989年提出处理确定不确定系统问题的系统分析方法——集对分析方法(Set Pair Analysis，SPA)[1]。SPA直接面对系统中客观存在的确定性和不确定性，视其为一个系统进行综合考虑，并予以辩证的同异反分析，其核心是把对不确定性的辨证思维转换成可计算的数学模型，其突出的优势是构建具有一定联系的两个集合，从整体和局部上分析研究对象之间内在的“确定性和不确定性关系”[1]，并用联系数的结构式[1-3]进行定量的数学处理，故又称为联系数学(Connection Mathematics)。人们已开始将SPA处理不确定性问题的特有的理论和方法，应用于数学、物理、系统科学、信息科学、管理科学、智能科学、经济学、灾害学、农业科学、水利科学、生态学、资源与环境科学、教育等众多领域，丰富了当今不确定性分析理论，为处理和应用水资源各种不确定性信息提供了具有广泛启发意义的新思路[3-6]。

在自然演化和人类活动的众多因子作用下，连接大气、海洋、湖泊、河流、地下水、冰雪、陆地、生物、人类等圈层的水资源系统充满着随机性、模糊性、灰色性、未确知性、分形、混沌等多种不确定性，是一个典型的复杂系统[5]。识别、处理和应用水文水资源系统的结构特征和行为特征的各种不确定性一直是近40年来水资源不确定性分析的研究热点，目前已提出了随机水文学、模糊水文学、灰色系统水文学、分形与混沌分析、地统计学、广义熵方法、未确知数学方法、属性识别理论、小波分析、计算智能等众多不确定性分析方法，在水文水资源分析计算、预测、评价和决策分析等领域中得到了广泛应用[4-9]。集对分析是一类能有效地处理水资源系统不确定性的新理论和新方法，开始得到一些应用[4-5]。本文旨在归纳、分析水资源集对分析理论与应用研究现状，探讨集对分析研究面临的主要问题和发展方向，以期进一步推动水资源集对分析理论和应用的发展，不断丰富集对分析的理论体系。

1 集对分析理论研究进展

1.1 集对分析基本原理

人们常常根据同一集合中所有元素的共同属性这一标准，来判断所论各研究对象是否属于该集合[8]。普通集合就是论域中的单个元素与某概念所论属性之间的一种确定性的定量关系(一元映射)，模糊集就是论域中的单个元素与某概念所论属性之间的一种(正向)概念外延不确定性的定量关系，可变模糊集就是论域中的单个元素与某概念所论属性之间的一种(正向、反向)概念外延不确定性的定量关系[6,8]。根据普遍联系原理，事物间常常在某些特定属性方面具有关联性，这些关联性的程度通常可用3个明显的特征(例如大中小、高中低、丰中枯、好中差、同异反等)来描述，称为三分原理，它是自然辨证法中正反两分原理的推广，是人们对客观事物的无限多样性不可能作彻底分析研究的一种反映。集对分析的核心思想就是把确定性与不确定性作为一个相互联系、相互制约、相互渗透，又可在一定条件下相互转化的确定不确定系统来处理[1-2,5]。将确定不确定性系统的两个有关联的集合作为集对，通过对集对的关系特性作同一性、差异性、对立性的分析，建立集对的同、异、反3种关系，并用联系度(联系数)的基本表达式(1)表征这些关系，对所论问题作进一步分析[1]：

μ=a+bi+cj。

(1)式中：a、b、c∈[0,1]，且a+b+c=1；a为集对的同一度；b为集对的差异度；c为集对的对立度，它们实际上就是所论属性的同、异、反3方面的模糊关系；i为差异度系数，取值区间为[-1,1]，有时仅起差异标记作用；j为对立度系数，一般取值为-1，有时仅起对立标记作用；a和cj是相对确定性的项；bi是相对不确定性的项，可统一描述随机性、模糊性、灰色性、未确知性、中介(反映客观事物相互过渡的各离散状态)不确定、信息不足等不确定性信息[1,3]。

用联系数可描述不确定性系统，能清晰地显示关系的整体和局部结构，形象地定量揭示复杂关系中的3种或多种秉性，可表征多种不确定性，特别是联系数具有如下主要作用[1,5]：①联系数把确定数a与其所在问题背景的范围a+b+c联系起来。②联系数把数与值联系起来，同一个确定数a与不同范围a+b+c联系在一起时，事实上会使该确定数具有不同的值。③联系数把宏观层次上的确定量a、b、c和j，与微观层次上的不确定量i联系起来，它们构成一个确定不确定系统，可统一描述和处理各种不确定性。④联系数把所论两个集合所具有的同一性、差异性和对立性模糊关系联系起来，其中同一性和对立性模糊关系是相对确定的，差异性模糊关系是相对不确定的，它们构成一个确定不确定模糊关系系统。基于这种联系，使得同一性、差异性和对立性模糊关系可相互转化。

1.2 集对分析基本概念

1.2.1 集对

根据系统成对原理，任何事物或概念都是成对地存在，概念上完全纯粹、单一的集合不能独立存在；换言之，在一般意义上泛指某一事物时，同时在有意无意地拿与该事物成对的另一事物作参考，例如在说某数是正数时，同时在有意无意拿负数作参考；在进行水文水资源评价时，就是将评价对象与评价标准在作参考[1]。集对是指在某特定属性方面有联系的两个集合组成的对子，如评价的水质对象与水质标准就是一个集对，其中待评价的水质对象用集合A表示，水质标准用集合B表示，则A和B就构成一个集对[1]。集对是集对分析的基础。集对分析认为集合是一个处于基底层次的元概念，面对受对立同一规律制约的客观对象，要求元素性质完全同一的一个集合去描述本意上是对立同一的一个客观对象，避免出现悖论，只有把集合概念提升到集对这个层次，承认矛盾，正视不确定性，给予客观承认、系统描述、定量刻画、具体分析，才能找出解决问题的方法。系统工程研究表明，描述同一个客观对象系统，至少需要两个集合[1]。“一定联系”是一个相对模糊的概念，一般是指同一性、差异性和对立性3方面的关系，其中对立性关系目前主要有5种类型[1,7]：互反型(倒数型)、互否型(有无型)、相反型(正负型)、互补型和共轭型(虚实型)。由于客观事物都是成对地存在，无法去孤立地认识和研究成对事物中的某一单个事物，而只能从成对的两个事物之相互联系、相互影响、相互渗透、相互制约和在一定条件下相互转化的过程中去认识和把握其中任一单个事物的有关规律[1]。

在水循环过程的变化环境背景下，水资源系统中普遍存在着各种各样的集合，按照不同的研究目的可组成适当集对，如降雨与径流、洪涝与干旱、汛期与非汛期、冲刷与沉积、蓄水与泄水、余水与亏水、降水与蒸发、相似与非相似、超过与不及、合格与不合格、安全与破坏、一般与特殊、输入与输出、稳定与非稳定、相关与非相关、丰与枯等[5]，这就为集对分析在水资源中的合理应用创造了先决条件。探求这些集对之间的不确定性关系正是水资源系统分析、预测、评价、决策、优化、模拟、推理和控制的基本前提和重要基础[5,8]。

1.2.2 联系度(数)

联系度(数)是集对分析处理问题的基本工具，实际应用中联系度、联系数的概念已趋于等同。式(1)为联系度(数)的基本表达式，在实际问题中，当其中的同一、差异、对立出现缺失项时，有

μ=a+bi，

(2)

μ=a+cj，

(3)

μ=bi+cj。

(4)

称式(2)为同异式，式(3)为同反式，式(4)为异反式[1]。

联系数的基本表达式是建立在对描述对象作“同、异、反”划分的基础上，称为同异反联系数或三元联系数；而在实际应用中仅对描述对象所处的状态空间作“一分为三”的划分，有时尚不够细化，为此，需对联系数表达式μ=a+bi+cj作不同层次的扩展[1,3,7]，称为联系数的可展性。对联系数进行扩展后成为多元联系数[1,3-4]：

(5)式中：ax、by、cz为联系分量，ax、by、cz∈[0,1]；i1,i2, …,in为差异度系数，取值区间为[-1,1]，有时仅起差异标记作用；j1,j2, …,jk表示对立度系数，取值规定为-1，有时仅起对立标记作用。

集对分析法就是在一定的问题背景下，对所论集对的特性展开同异反分析，并用联系度(联系数)加以辩证分析、全面度量和深刻刻画，得到集对的同异反联系数表达式，利用联系数及其运算深入展开有关系统的联系、演化、诊断、识别、模拟、预测、评价、预警、决策、控制等问题的研究，其中差异度系数的计算是应用集对分析法的一个关键问题[1-5,8-9]。

1.2.3 集对势

当联系度μ=a+bi+cj中的c≠0时，同一度a与对立度c的比值(a/c)定义为所论集对H在指定问题背景下的联系势或集对势，记为shi(H)=a/c，集对势可划分为3类[1]：①集对同势：shi(H)=a/c>1，说明客观系统之间存在同一趋势；②集对反势：shi(H)=a/c<1，说明客观系统之间存在对立趋势；③集对均势：shi(H)=a/c=1，说明客观系统之间的联系处于稳定状态。根据集对势shi(H)的大小，可以界定集对势的等级和次序关系，集对势在评价、排序、预测等方面开始得到许多应用[1,3-4]。

周家红等[10]提出了悲观势和乐观势的概念：悲观势是指系统从悲观的角度出发，将所有不确定项(差异度)均转化为对立项(对立度)，用系统中的同一项(同一度)与对立项(对立度)的比值来研究系统的趋势；乐观势是指系统从乐观的角度出发，将所有不确定项(差异度)均转化为同一项(同一度)，用系统中的同一项(同一度)与对立项(对立度)的比值来研究系统的趋势。李德顺[11]、张春英[12]为解决集对势定义存在的问题，基于相对同一度和相对对立度提出了广义集对势；为避免集对势定义中c≠0必要条件的影响，潘争伟等[13]利用指数函数改进传统集对势，建立集对指数势的概念。

1.2.4 偏联系数

偏联系数是在联系数理论基础上提出的一种反映研究对象发展趋势的伴随函数[1,14-15]。设有联系数μ=a+bi+cj，其中a、b、c∈[0,1]，a+b+c=1，i∈[-1,1]，j=-1，则有[15]：

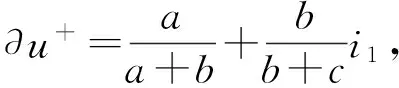
(6)

(7)

(8)

式中:i1、i2为差异度系数，取值区间为[-1,1]。

式(1)表示的是同异反状态联系数；式(6)表示了联系数的正向发展趋势，反映了联系数的一种正向(同向)变化趋势，称为偏正联系数；式(7)表示了联系数的负向发展趋势，反映了联系数的一种负向(反向)变化趋势，称为偏负联系数；式(8)反映了联系数的一种综合发展趋势，称为全偏联系数，当全偏联系数分别大于零、等于零和小于零时，分别称为正向发展趋势、临界趋势和负向发展趋势[15-16]。

1.2.5 联系变量与联系函数

联系变量是指在宏观层次上随时间t等因素变动着的联系数，如μ(t)、μ(x)等；若联系变量μ(y)的变化由另一个联系变量μ(x)引起，则称μ(y)是μ(x)的联系函数，其中μ(x)为自变不确定量、μ(y)为因变不确定量[1]。PAN Zhengwei等[17]根据联系变量的函数特点，给出了联系函数和复合联系函数的概念。

1.3 联系数的确定

联系数的计算思路为先确定联系数表达式，其实质是确定联系分量;再确定差异度系数;最后通过运算进一步确定联系数[1-5,18-19]。

1.3.1 联系数表达式

文献[1]中赵克勤给出了联系度的定义式，以及穷举法、逐步分析法、层次分析法、直接比较法、最大最小法、确定不确定法和比例法等，均是采用定义法确定联系数表达式[2,18-19]。李祚泳[20]、李凡修等[21]提出了一种“宽域式”函数结构方法确定联系分量；邱林等[22]采用属性识别法确定联系分量；潘争伟等[23]、汪哲荪等[24]在改进属性识别法基础上，提出了符合集对分析基本思想“一分为三”的“层次分析法”联系数表达式确定方法。

1.3.2 差异度系数

差异度系数是联系数描述不确定性的主要体现，差异度系数的取值目前仍是集对分析研究的热点和难点。赵克勤[1]给出的方法主要包括顺势取值法、逆势取值法、计算取值法、特殊值法等；余国祥[25]提出了随机取值法；王霞等[26]给出了概率取值法和函数模拟法；汪新凡[27]提出“均分原则”确定差异度系数；吴亭[28]提出公式法确定差异度系数；朱兵等[29]、王红芳[30]提出统计试验法确定差异度系数；李祚泳等[31]提出遗传算法优化确定差异度系数；郭瑞林等[32]、李陶等[33]用灰色系统理论中的绝对关联度概念计算差异度系数；潘争伟、陈南祥等[34-36]提出了基于三角模糊数的差异度系数和基于梯形模糊数的差异度系数的确定方法。以上各种方法均有其优势，需要具体分析实际问题，确定相应的差异度系数。

1.4 集对分析扩展

近年来，集对分析研究思路不断扩展，出现了集对分析与模糊集、可拓学等方法的融合[18]以及联系数与区间数、三角模糊数等之间的转换。

1.4.1 模糊联系数

1.4.2 联系数与物元

利用集对分析中的联系度刻画物元之间同异反联系程度的数为物元联系数[39]。设U1、U2为两物元，则物元联系数的一般形式为：

μ(U1,U2)=a+bi+cj。

利用联系数表示物元的特征值，称为联系数物元[40-41]，其一般形式为：

偏联系数物元[42]的一般形式为：

1.4.3 模糊数联系数

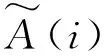
1.4.4 联系数与概率

随机事件A在某次随机试验中发生的可能性大小P(A)与不发生的可能性大小[1-P(A)]可以用联系数的形式表示为[49]：

Pc(A)=P(A)+[1-P(A)]i，

(9)

式中Pc(A)为联系数意义下事件A在某次随机试验中发生的可能性大小P(A)(A的大数概率)与不发生的可能性大小1-P(A)(A的即或概率)的“联系和”(也称联系概率)。

(10)

1.4.5 联系数与区间数

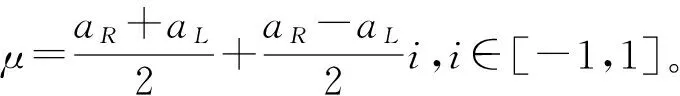
1.4.6 联系数与三角模糊数

1.4.7 联系云

传统云模型虽能描述研究问题的随机性和模糊性，但忽视了指标值分布的有限区间性以及结果在相邻等级间的转化关系。为克服传统云模型对指标分布要求的局限性，汪明武等[2]将联系数理论引入云滴生成过程，实现了模拟云滴真实代表评价指标的实际分布特点，并能定量描述指标与评价等级间的确定和不确定关系，这有助于云模型的实际应用。

2 水资源集对分析应用研究进展

在变化环境下如何有效地识别、建立和应用与水资源研究对象时空演变过程有关的各种不确定性关系，主要包括在时间演变过程中前后的关系、空间分布上的关系、研究对象之间属性方面的关系，通过寻求各种关系以达到对水文水资源现象的分析、预测和评价[5]。各种水资源系统转换/模型的建立，主要就是基于上述各种关系及其运算。由于水文水资源系统输入、转换的不确定性，水文水资源现象的分析、预测和评价结果等系统输出理论上均应是不确定性的，而不是一个固定的计算结果[5,24]。要科学地建立这些“关系”，首要问题在于剖析和掌握“关系”的性质。在气候变化和人类活动的影响下，这些关系可能是线性的，也可能是非线性的；可能是静态的，也可能是动态的；可能是随机性的，也可能是模糊性的、灰色性的；可能是未确知性的，也可能是多种特性的综合[5]。如何识别、处理和应用水资源现象的各种不确定性关系一直是水资源研究领域的核心问题[5-6]。SPA的一般应用过程，就是按照对实际不确定性予以客观承认、系统描述、定量刻画、具体分析的方法论[1]，把组成集对的两个集合A与B间的某关系属性中的不确定性和确定性作为一个系统加以处理，在一定的研究问题背景下，对集对(A,B)的特性空间同时进行同一性关系、差异性关系、对立性关系的分析，通过建立两个集合的同异反联系数(度)表达式来构造该模糊关系属性的相对隶属度函数，进而可进行分析、预测和评价各种不确定性问题等[1-2,4-5]。集对分析在处理不确定性复杂问题方面具有分析问题全面、精细、广泛等显著特点，已被广泛应用于许多学科，近10年来在水资源评价、决策、预测、相关分析、相似分析、诊断识别、推理等领域也取得了重要进展。

2.1 水资源系统集对分析评价应用

现有的各种水资源系统分析综合评价方法，一般均包括为实现系统分类排序这一评价总目标，如何合理地确定评价对象集生成函数、评价指标集生成函数、评价指标测度函数、定性指标定量化函数、单指标评价函数(指标一致无量纲化函数)、指标权重函数和综合评价指标函数这7个函数的过程，确定上述7个函数的过程中显然存在许多不确定性问题[53]。基于集对分析的水文水资源系统评价方法，就是应用SPA构造上述7个函数的各种方法，特别是建立基于联系数的单指标评价函数，来处理如何在随机、模糊等不确定性环境下构建评价指标与评价等级标准之间合理的定量评价模型这一关键问题[4-5]。金菊良等[54]建立了基于联系数的流域水安全评价模型，用该模型可从指标、子系统和样本3个层次定量地分析流域水安全的复杂状态，既可测度流域水安全整体状态的高低程度，又可识别影响流域水安全状态的重要指标和重要子系统；吴开亚等[55]用集对分析方法构造了流域水资源安全评价样本符合评价等级标准的可变模糊集的相对隶属度的新方法，再用模糊综合评价方法建立了流域水资源安全定量评价模型；WANG Wensheng等[56]基于集对原理提出了水资源系统评价新方法——集对评价法，探讨了集对评价法在水资源系统评价中的应用；WANG Yingchao等[57]基于集对分析理论，确定评价指标的等级联系度，建立了基于集对分析的岩溶隧道突水风险评估模型；杨鑫等[58]综合考虑支持力指数、压力指数和协调指数3个方面，筛选出影响水资源承载力变化的7个代表性指标，运用集对分析和熵权赋值的方法构建了基于集对分析理论的云南省水资源承载力评估模型；黄瑞等[59]通过细化同异反特性，对标准集对分析方法进行改进，并应用于大伙房水库水质评价中；沈俊源等[60]建立了“最严格水资源管理制度的三条红线”为基准的水安全量化指标体系，采用模糊联系度和置信度准则，建立了基于信息熵的水安全模糊集对评价模型；曹永强等[61]采用模糊模式识别法对全国水资源系统脆弱性进行评价，同时采用集对分析法和投影寻踪法与其进行对比；YUE Wencong等[62]提出混合生命周期和模糊集对分析方法，分析了大规模工业废水排放对生态环境的影响；YANG Fengguang等[63]提出了区域泥石流危险度评估的集对分析和改进的集对分析不确定性模型，将模型应用于中国四川省北川县7个镇的泥石流危险性评价中。

随着集对分析方法在系统分析评价中的推广应用，出现了集对分析与其他系统评价方法的耦合模型。叶章蕊等[64]基于集对分析理论与模糊层次分析法构建了模糊联系度水质评价模型，将熵值赋权法和超标加权法引入该模型，并通过理想点法进行权重的合成，建立了组合权重模糊联系度模型，用于闽江渔业水域水质评价；杨哲等[65]将联系度与灰色聚类系数相结合，用联系度分量代替聚类系数，处理聚类系数中差异性较小的情况，采用指数型函数对传统白化权函数进行改进，建立了改进灰色聚类-SPA耦合的河流健康评价模型；ZOU Qiang等[66]提出了基于集对分析和可变模糊集的中国靖江分蓄洪区洪水风险评估模型；JIN Juliang等[67]建立了基于BP神经网络和集对分析的水资源可持续利用预警模型，并应用于中国云南哈尼梯田水资源可持续利用预警中；范荣亮等[68]应用集对理论和指标值属性测度，建立了节水型生态城市的健康评价模型；吴开亚等[43]用三角模糊数表示差异度系数，建立了基于三角模糊数截集的联系数评价模型，所得的评价等级为一置信区间数，并利用区间数的期望-方差排序法对评价结果进行了综合排序。

2.2 水资源系统集对分析决策应用

水资源系统决策分析方法主要是处理以益损值为目标函数、行动方案为优化变量、自然状态为约束条件的一类优化问题的各种方法，也就是以行动方案为评价对象的一类特殊的系统评价方法[53]。水资源系统决策过程需要处理物理、事理和人理方面的许多不确定性问题。基于集对分析的水文水资源系统决策分析方法就是应用SPA构建水资源系统决策方案优选的各种方法，显然，各种基于集对分析的水资源系统评价方法可以直接应用于优选水资源系统决策方案。此外，基于联系数、集对势、偏联系数或SPA与其他方法的耦合，利用水资源系统决策方案集的特定主、客观信息也可构建水资源系统决策分析新方法[4-5,18,53]。

韦美雁[69]构建了区间数上、下界偏差函数，并根据偏差越小越好的原则将区间数权重转化为确定性的权重向量，将区间决策矩阵转化成联系数决策矩阵，得出满意度最高的联系数，根据各个方案与最高满意度的比较得出差异度，提出了一种基于最小偏差的联系数排序方法；吴征等[70]通过证据理论分析各评价指标在指标集中的总距离，计算了各评价指标的可信度，基于此，确定各评价指标的权重，采用基于集对分析理论的评价方法，对每个评价指标与最优集指标的同一性和差异性进行了定量研究；唐言明等[71]从投票模型原理出发，进一步分解差异度，再次分解为同一度、差异度和对立度，提出了基于集对分析广义联系度函数的复杂系统方案优选模型，对城市防洪标准方案优选进行了分析；王伟等[72]考虑方案优先的不确定性处理和动态发展两方面因素，研究了偏联系数在城市污水处理方案优选中的应用；HU Junhua等[73]基于离差最大化思想构建优化模型，确定准则权重，提出了一种基于累积前景理论和集对分析的决策方法，并通过一个风险投资问题验证了该方法的有效性；CAO Yongxi等[74]根据离差最大化，确定各随机变量的概率，将区间型概率问题转化为经典的确定型概率问题，利用集对分析建立规划模型，将区间状态值用联系数表示，根据集对势序准则对方案进行排序，提出了基于集对分析的区间型随机直觉多准则决策方法；KUMAR等[75]提出了基于集对分析联系数的TOPSIS模型，以解决区间型直观模糊数属性值定义的区间型直观模糊集决策问题；董增川等[76]选择可供水量、利津入海水量、龙羊峡水库期末水位等10项指标为评价体系，在模糊优选法、灰色关联分析法、集对分析法等评价方法的基础上建立了黄河流域水量调度方案的组合决策模型。

2.3 水资源系统集对分析预测应用

水资源的丰枯变化预测是区域水安全管理的重要内容。在大气环流、太阳活动、前期水文气象要素、区域覆被变化等众多物理因子的综合作用下，水资源系统是一个弱相依、高度复杂的非线性动力系统，目前常用的预测方法可大致分为成因预测方法和统计预测方法[77]。但成因动力预测仍极为困难，而统计预测因其适用性强至今广为采用。统计预测主要包括时间序列分析法、多元统计法和相似预测法，由于水资源过程的自相依性不强，水资源与其影响因子之间关系复杂，因此用前两种统计预测方法建立有效的预测模型较为困难[77]。水文水资源系统预测就是在充分描述和揭示预测对象系统的发展变化规律的基础上，运用系统的关联性、延续性、相似性、不确定性、反馈控制等科学原理和方法，根据预测对象系统或其类似系统发展变化的实际数据、历史资料以及各种经验、判断和知识等，建立预测对象与预测因子之间的关系模型，根据关系模型和预测因子的最新变化信息，对预测对象系统在未来一定时期内的可能变化进行推测、估计、分析和评价，以指导系统的决策分析，减少对系统未来状况认识的不确定性和决策的盲目性[4-5]。上述水资源系统预测过程中存在诸多不确定性问题，使得预测对象系统在未来一定时期内的变化可能蕴含多种不确定性，基于集对分析的水资源系统预测方法，就是应用SPA识别和构造预测因子、从同异反3方面建立预测因子与预测对象之间的联系数，再建立基于联系数的预测模型，或与其他预测方法构建组合预测模型，用以确定预测结果。目前，应用较为广泛的集对分析预测方法主要有：基于集对分析的相似预测方法、基于集对分析的聚类预测方法、基于集对分析的自组织预测方法、基于集对分析的秩次预测模型和基于集对分析的组合预测方法等[4-5]。

冯利华等[78]反复调整预测因子各区段的分界值，可使水资源要素计算等级和实际等级的历史拟合率达到最大，提出了水资源变化趋势预测新方法；金菊良等[77]提出用集对分析检验和互相关系数统计假设检验相结合识别影响水资源变化的主要物理因子，从同异反3个方面定量刻画水资源历史样本之间的相似性，建立了基于集对分析的水资源相似预测模型；徐源蔚等[79]针对地下水位样本之间的相似性及影响因子与地下水位之间具有的确定性、不确定性特征，从同异反3个方面定量刻画地下水位的当前样本与历史样本之间的相似性，建立了基于集对分析的地下水位相似预测模型；吴新新[80]以向量之间的夹角、相关系数、欧式距离以及向量的模为指标对径流集合建立对应的指标集合，将指标集合的相似度作为判断径流集合相似度的依据，建立了以几何形式表示集对的G-SPA模型，对新疆黄水沟年径流量进行了预测；张云云等[81]通过对生活用水量的影响因子——人口总数的长期预测，利用集对分析联系度思想建立了集对分析聚类预测模型，对中国2015—2025年的生活用水量进行预测；和蕊等[82]结合了集对分析中的同异反模式识别的“择近原则”和聚类分析的基本思想进行分类预测，建立了城市生活需水量聚类预测的模型；万星[83]将径流量以及相应的气象资料、环境因素联系起来考虑，应用聚类分类构建这些类别与参照系统所组成的集对的同异反联系度，建立了基于集对联系度的水文径流量状态预测方法，并以新安江水库1955—1973年的相关历史数据资料为例进行了分析和计算；汪哲荪等[84]依据年径流量与其影响因子关系复杂的特点以及自组织数据挖掘理论分析和描述两者之间的联系，以集对分析为基础从同异反3个方面来刻画模型计算值与实际值之间的接近程度并建立了相应的筛选准则，以进行中间模型的评价及选择，从而构建了基于集对分析的年径流自组织预测模型；FENG等[85]采用集对分析方法对水资源物理因素进行模拟计算，以此对新疆伊犁河雅马渡站的径流量进行了预测分析；段先前等[86]建立了由12个影响因素组成的岩溶塌陷危险性预测指标体系，将影响因素实测值分别与危险性等级评价标准组成集对，建立了岩溶塌陷危险性预测模型；张金萍等[87]用小波分析方法对降雨量和参考作物腾发量进行多时间尺度分解，用SPA分析不同时间尺度下的降雨量和参考作物腾发量之间的同一性、差异性和对立性，探讨了北京市降雨量和参考作物腾发量的演变规律以及二者之间的关系；李深奇等[88]通过对量化标准系数进行率定，提出了率定量化标准系数的SPA长江宜昌站年径流预测模型；卢家海[89]利用集对分析对人工智能BP模型、小波BP模型及GA-BP模型的径流预测结果进行同异反分析，建立了基于集对分析的小浪底水库径流组合预测模型；郭彦等[90]提出了基于集对分析的区域需水量组合预测模型。

2.4 水资源系统集对分析相关和相似分析应用

联系数μX-Y=a+bi+cj中，可用a表示xi、yi具有相同变化趋势时的正相关程度，用c表示xi、yi具有相反变化趋势时的负相关程度，用b表示xi、yi的变化趋势不明显时存在的不定相关程度[5,77]。可见联系数显示了X-Y关系的整体结构(μX-Y)和局部结构(a,bi,cj)，定量揭示了复杂关系中的3种或多种秉性，克服了随机分析中的相关系数、模糊分析中的隶属度和灰色分析中的灰色关联度单一指标表征关系的局限，具有独特优势[5]。

王文圣等[91]考虑径流的大小及其年内时程分配，将径流量分别分类并构造分类集合，由分类集合与分类标准集合构造集对，用联系度描述集对的关系进行径流丰枯分类，提出了年径流丰枯分类新方法——集对分析法；王文圣等[92]针对现有的水文相关分析只能描述水文变量之间宏观上的相关关系这一不足，提出了用集对分析的联系度刻画水文变量之间微观上的相关结构，分析了相关结构中各种关系成分所占的比例和性质，提出了基于集对原理的因变量主要影响因子的识别方法，并用于径流回归分析中；符秋菊等[93]利用集对分析联系度原理，以广西北部湾河流水系为例进行了水文分析、分类及相似性选择计算；蒋尚明等[94]用集对分析方法分析了粮食单产波动分量与其影响因子之间的相关性，量化分析各影响因子对粮食单产波动的综合影响率；杨淇翔等[95]用广义集对势从联系趋势的角度进行径流丰枯分类，提出了基于广义集对势判别准则的年径流丰枯分类模型，并将该模型应用于黑河莺落峡水文站的年径流丰枯分类中；温孟婵等[96]考虑径流丰枯分类标准边界的模糊性，建立了模糊联系度，并结合径流年内分配，赋予权重因子，得到加权联系数，判断年径流的丰枯等级，提出了采用加权模糊集对分析法；蒋尚明等[97]用近邻估计方法，通过计算各个预测因子的变异系数来判断预测因子在某次预测中处于强势或者弱势，动态地选择预报功能强的强势因子，消除对预报起负面作用的弱势因子的作用，据此建立了基于近邻估计的年径流预测动态联系数回归模型；万晨等[98]基于协同学基本原理，以集对分析中的联系度代替协同度，构建了水资源与社会经济系统协同评价模型，对安徽省16个地级市2007—2013年的水资源与社会经济系统发展的协同情况进行分析；周戎星等[99]采用集对分析方法量化影响生产、生活、生态用水的驱动因子与用水量之间的联系大小，识别用水量主要驱动因子，提出了基于集对分析的区域用水量驱动因子分析模型，对山东省用水量驱动因子进行定量分析。

2.5 水资源系统集对分析诊断识别和集对推理应用

随着集对分析应用范围的不断扩展，在诊断识别、推理方面的应用成果不断出现。吴开亚等[100]用联系数方法构造了流域水安全评价指标样本值隶属于可变模糊集“水安全诊断评价标准等级”的相对隶属度函数，建立了流域水安全诊断评价模型，用该模型综合评价了流域水安全评价指标各时期样本系列，若流域水安全系统或其子系统的安全状况处于临界安全以下，则根据联系数值识别出使流域水安全系统或其子系统处于不安全的主要子系统及其主要指标，对这些指标提出相应的调控措施后，再次综合评价流域水安全系统或其子系统的总体安全状况；李宜敏等[101]利用集对分析联系度，对稀疏数据矩阵进行同异反特征分类，给出了符合一定概率分布的同异反特征数，并由此给出了同异反距离的计算方法，根据距离聚类方法确定聚类结果，并应用于信息分类中；黄大荣等[102]通过分析可能引起BA系统故障的各种因素，建立了系统的故障树模型，确定了系统故障原因的各种可能组合方式，引入中间状态概率的概念，结合集对分析联系数理论建立了基于集对分析联系数和故障树理论的BA系统的可靠性分析方法；欧开灿等[103]在预测与对比事物的类比中进行同异反分析，基于此，建立了类比推理预测的联系度模型，对原类比推理的预测结果加以改进，得到了区间预测值和点预测值；吴开亚等[104]用基于加速遗传算法的模糊层次分析法筛选指标体系、确定各评价指标权重，用BP神经网络模型滚动预测评价指标，用集对分析方法构造评价指标样本值隶属于可变模糊集“水安全评价标准等级”的相对隶属度函数，建立了流域水安全预警评价的智能集成模型；成科扬[105]从模糊关系的角度，建立了基于集对分析的模糊推理理论，并将模糊推理数量化；马守明等[106]提出一种利用同异反向量夹角余弦来对不确定上下文进行推理的方法，对智能空间场景中不确定上下文状态进行了推理分析；蒋云良[107]讨论了基于集对分析联系数的同异反定量“推理路径”的选择，给出了路径选择的一般规则，并应用于学生成绩推算；陈悦莲[108]通过建立联系数矩阵以及推理，将不确定性问题通过定量分析，即考虑同一度最大、对立度最小的析取推理，建立了方案的优劣排序，讨论了集对推理评优及其应用；赵森烽等[49]在定义了联系概率的基础上，对联系概率(复概率)在不确定性推理中的应用进行了分析；杨亚锋[109]提出了集对关系的概念，以集对逻辑为基础，给出了集对蕴含式的定义，讨论了单论域上集对推理的基本模式与方法，并将单论域推理方法延伸至具有集对关系的联系域上；孙杰[110]提出集对逻辑的概念及演算规则、模糊集对推理的基本概念和基本形式，讨论集对效用函数的三维优先关系，给出了格结构的构建原理与方法，建立了基于集对效用函数的格序决策模型，并结合决策原理，建立了基于集对推理的格序决策模型；王会芳[111]定义了案例集对的相关概念，提出了一种基于集对分析的案例相似度计算模型，构建了基于集对分析的案例推理检索模型，并对中医喘证本体案例推理进行了应用分析；李丽红等[112]提出了模糊集对推理与决策方法，并相应开展了许多应用。

3 集对分析的发展趋势

作为一种新颖的不确定性分析方法，集对分析用联系数和联系数值表征和处理研究对象之间的不确定性关系。联系数其实就是不确定性系统的一个数学模型。上述水资源集对分析理论与应用研究表明，集对分析具有概念清晰、原理简明、计算方便和结果合理的优点。SPA自提出至今已有近30年的研究历史，作为一种新的不确定性分析理论和方法，目前仍处于不断的发展阶段，新的理论与方法的发展之路还很漫长。近年来，集对分析的研究主要集中在应用研究方面，而作为新的理论与研究方法，需要以坚实的理论基础为基石，而目前，集对分析的理论基础研究尚显薄弱，尚无很完整的理论和方法体系，特别是如下主要问题亟待今后深入研究。

1)集对分析原理的深度探索[5]：①从哲学层面深度探索集对分析表征的不确定性本质；②探索不确定性关系表达式——联系数(值)的合理性和科学性；③探索联系数或联系数值与不确定性程度的定量关系，无需限定集对中两集合的元素数目相等，两集合元素间的对比应在元素序偶中展开，对比方式应采用“符合某种关系的情形”来进行[3]；④在集对分析框架下，综合运用随机性、模糊性、灰色性、混沌性等不确定性探索不确定性关系的定量表征。

2)相关概念与传统数学概念探讨：集对分析理论在发展过程中，提出了复联系数、联系概率、偏联系数、反偏联系数、联系熵等相关概念，这些概念的定义与传统数学概念存在偏差，如偏联系数与偏导数、联系熵与传统熵在含义上并不一致[19]。

3)相关概念定义的一致性研究：在集对分析被广泛应用的过程中，相关概念得到丰富和发展，如将联系度定义为联系数，联系数扩展为多元联系数，提出复联系数、区间型联系数、联系概率和自然数的联系数化等概念，以及集对势、态势联系数、偏联系数、反偏联系数、联系熵、邻联系数、相互作用联系数、多重联系数、多重多元联系数等联系数伴随函数。上述概念的使用目前多较为随意，完全凭借作者的主观臆断，没有形成概念上的统一。

4)同异反划分标准的确定：第1种情况是问题本身给出了分级标准集(例如：上中下、优中差、高中低等3级)，这时只要把需分级的研究对象与给定的标准集对照，同一级内谓之同，邻级谓之异，隔级谓之反[5]。分级标准是4等级集合时，采用四元联系数；5等级集合时，采用五元联系数，依次类推。第2种情况是问题本身没有给出分级标准，这时需要考虑同异反分级的界线定在何处合适，定得合适，得到的分析结果往往比较满意，反之结果就会不满意，为此需要通过调试寻找同异反的最优分界位置[5,78]。

5)差异度系数i或i1，i2，…，in的合理取值：集对分析区别于其他不确定性理论的一个显著特点是，在联系数中设置了一个不确定数i，而i取值的不确定成为了集对分析理论和应用发展的难点。集对分析给出i取值的原则是，把面向联系数本身的理论取值与面向研究对象的实际情况取值相结合，把时序变化统计取值与因素空间的因素分析相结合，把i的不确定取值与确定性、不确定性相互作用取值相结合，简称为三结合取值原则[1,16,111]。至于具体的取值方法，有随机抽样取值、统计取值、函数取值、顺势取值、比例取值、黄金分割取值、分解取值、定义取值、优化取值、取特殊值，特别是取i=μ等，无论何种取值，至少要体现出某种结合；取何值较为合理，需要回到原问题，面向研究对象来选择；取定i的一个值后，从数学上看，是对b作了一次分解，把b分解成bi1和b-bi1两部分，是把这两部分客观反映(这时二元联系数将变成三元联系数)，还是把bi1并入a，把b-bi1仍用(b-bi1)i表示，也需根据不同的问题要求来选取；此外i取值也可随集对的时间演变而变化[1,16]。

6)集对分析与其他方法相结合：集对分析之所以称为“集对分析”，从方法论上就要求在处理1个问题时，需要同时采用2种或2种以上的处理方法，对采用不同方法出现的结果不同时，作同异反分析，取长补短[1-5,112-113]。集对分析与模糊集方法、随机模拟方法、信息熵方法等结合是集对分析能不断创新、发展、提高的一个重要研究经验。

4 结语

水资源集对分析的研究与应用领域不断扩展，取得了丰硕的研究成果，几乎涉及了与水资源相关的所有研究领域，拓展了水资源学科的研究内容，丰富、完善了传统的水资源分析、计算、预测、评价和决策方法，具有重要的学术意义和实用价值。目前，集对分析的研究尚存在众多亟待解决的理论问题，集对分析基础概念、四则运算等需要规范和明确，理论体系需要不断完善等。应用领域研究需要不断拓展，需要建立集对推理、集对控制、集对预测和集对决策等新方法，这些新方法的理论思路、应用范围需不断完善，以便不断丰富集对分析理论体系。

[1]赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社,2000.

[2]汪明武,金菊良.联系数理论与应用[M].北京:科学出版社,2017.

[3]蒋云良,徐从富.集对分析理论及其应用研究进展[J].计算机科学,2006,33(1):205-209.

[4]潘争伟,吴成国,金菊良.水资源系统评价与预测的集对分析方法[M].北京:科学出版社,2016.

[5]王文圣,李跃清,金菊良,等.水文水资源集对分析[M].北京:科学出版社,2010.

[6]陈守煜.水资源与防洪系统可变模糊集理论与方法[M].大连:大连理工大学出版社,2005.

[7]刘颖,于冬梅,程显毅.联系数学中的几个问题[J].数学的实践与认识,2004,34(10):77-82.

[8]沈时兴,金菊良,宋松柏,等.水文水资源集对分析的理论基础探讨[J].合肥工业大学学报(自然科学版),2013,36(12):1481-1488.

[9]李陶.集对分析理论及其在水土资源系统分析中的应用[D].哈尔滨:东北农业大学,2010.

[10]周家红,许开立,陈志勇.系统动态安全评价研究[J].东北大学学报(自然科学版),2008,29(3):416-419.

[11]李德顺.基于广义集对分析的系统危险性评价研究[D].沈阳:东北大学,2010.

[12]张春英.基于属性图的社交网络建模与态势分析理论研究[D].秦皇岛:燕山大学,2013.

[13]潘争伟,吴成国,周玉良,等.基于集对指数势的流域水资源系统脆弱性影响因子分析[J].水电能源科学,2014,32(3):39-43.

[14]王万军.基于偏联系数的决策模型及其应用[J].唐山师范学院学报,2009,31(5):32-34.

[15]覃杰,赵克勤.基于偏联系数的医院医疗质量发展趋势综合分析[J].中国医院统计,2007,14(2):127-129.

[16]赵克勤,赵森烽.奇妙的联系数[M].北京:知识产权出版社,2014.

[17]PAN Zhengwei,JIN Juliang,LIU Li,et al.Risk evaluation of natural disasters based on connection function[J].Chinese Journal of Population Resources and Environment,2013,11(2):118-124.

[18]汪明武,金菊良,周玉良.集对分析耦合方法与应用[M].北京:科学出版社,2014.

[19]蒋云良,赵克勤,刘以安,等.信息处理集对分析[M].北京:科学出版社,2015.

[20]李祚泳.环境质量评价原理与方法[M].北京:化学工业出版社,2004.

[21]李凡修,梅平,陈武.区域生态环境质量的集对评价模型及应用[J].环境工程,2006,24(3):77-78,89.

[22]邱林,冯晓波,冯丽云,等.集对分析法在湖泊水质富营养化评价中的应用[J].人民长江,2008,39(5):52-54.

[23]潘争伟,吴开亚,金菊良,等.水资源可再生能力评价的集对分析方法[J].水电能源科学,2009,27(5):24-26,93.

[24]汪哲荪,金菊良,魏一鸣,等.三角模糊数随机模拟的防洪工程联系数风险评价模型[J].水利学报,2010,41(10):1173-1178.

[25]余国祥.对联系数中的不确定数i的研究[J].辽宁师范大学学报(自然科学版),2002,25(4):349-352.

[26]王霞,彭晓华.集对分析中差异度系数i的取值方法及应用[J].天津轻工业学院学报,2003,43(4):56-58.

[27]汪新凡.基于模糊语言评估和联系数的多属性群决策方法[J].数学的实践与认识,2007,37(15):54-59.

[28]吴亭.联系数a+bi中不确定系数的一个取值公式及应用[J].科技通报,2008,24(5):595-597.

[29]朱兵,王文圣,王红芳,等.集对分析中差异不确定系数i的探讨[J].四川大学学报(工程科学版),2008,40(1):5-9.

[30]王红芳.集对分析在水文水资源中的应用研究[D].成都:四川大学,2008.

[31]李祚泳,邬敏,刘智勇,等.联系数中i赋值的新途径及在水质评价中的应用[J].四川大学学报(工程科学版),2009,41(1):8-13.

[32]郭瑞林,刘亚飞,王景顺,等.小麦品种区域试验同异分析中不确定系数i的求解及其应用[J].麦类作物学报,2010,30(6):1160-1164.

[33]李陶,付强,丁红.基于灰色关联度的集对分析差异系数研究[J].黑龙江水专学报,2010,37(1):97-99.

[34]潘争伟,吴开亚,金菊良,等.湖泊水质富营养化评价的集对分析与三角模糊数耦合模型[M]∥赵克勤,米红.非传统安全集对分析.北京:知识产权出版社,2010:89-97.

[35]陈南祥,杨淇翔.基于博弈论组合赋权的流域水资源承载力集对分析[J].灌溉排水学报,2013,32(2):81-85.

[36]潘争伟,金菊良,周戎星.基于梯形模糊数联系数的评价方法及其应用[J].水利水电科技进展,2016,36(5):69-74.

[37]张斌.多目标系统决策的模糊集对分析方法[J].系统工程理论与实践,1997(12):108-114.

[38]王万军.基于FSPA的高校教师职称评定方法及应用[J].安徽理工大学学报(社会科学版),2008,10(3):73-75.

[39]谢砚青.物元联系数及其应用初探[C]∥集对分析与界壳论研究与应用论文集.北京:气象出版社,2002:105-109.

[40]王英杰.基于联系数的物元模型及其应用初探[C]∥全国集对分析暨联系数学学术研讨会会议论文集,2004.

[41]邬敏,李祚泳,刘智勇,等.基于联系数的水质评价物元模型[J].水文,2008,28(6):57-60.

[42]王松,贺仲雄.集对分析SPA的新进展：SPE与SPF[J].计算技术与自动化,2006,25(4):171-173.

[43]吴开亚,金菊良,潘争伟.基于三角模糊数截集的联系数模型在城市涝灾影响等级评价中的应用[J].水利学报,2010,55(6):711-719.

[44]张平.基于SPA的Rough集：一种数据挖掘的新方法[D].杭州：浙江工业大学,2000.

[45]刘保相.粗糙集对分析理论与决策模型[M].北京:科学出版社,2010.

[46]PAN Zhengwei,WU Kaiya,JIN Juliang,et al.Assessment model of set pair analysis for flood loss based on triangular fuzzy intervals underα-cut[C]∥2009 Chinese Control and Decision Conference,2009:3562-3567.

[47]潘争伟,金菊良,吴开亚,等.区域水环境系统脆弱性指标体系及综合决策模型研究[J].长江流域资源与环境,2014,23(4):518-525.

[48]潘争伟,金菊良,刘晓薇,等.水资源利用系统脆弱性机理及评价方法研究[J].自然资源学报,2016,31(9):1599-1609.

[49]赵森烽.赵克勤.概率联系数化的原理及其在概率推理中的应用[J].智能系统学报,2012,7(3):200-205.

[50]刘秀梅,赵克勤.基于联系数不确定性分析的区间数多属性决策[J].模糊系统与数学,2010,24(5):141-148.

[51]王万军.基于模糊语言的多属性联系数决策方法[J].数学的实践与认识,2008,38(12):78-82.

[52]刘秀梅,王传斌,赵克勤.基于联系数的三角模糊数多属性决策新模型[J].统工程与电子技术,2009,31(10):2399-2403.

[53]金菊良,魏一鸣.复杂系统广义智能评价方法与应用[M].北京:科学出版社,2008.

[54]金菊良,吴开亚,魏一鸣.基于联系数的流域水安全评价模型[J].水利学报,2008,39(4):401-409.

[55]吴开亚,金菊良,周玉良,等.流域水资源安全评价的集对分析与可变模糊集耦合模型[J].四川大学学报(工程科学版),2008,40(3):6-12.

[56]WANG Wensheng,JIN Juliang,DING Jin,et al.A new approach to water resources system assessment:set pair analysis method[J].Sci China Ser E-Tech Sci,2009,52(10):3017-3023.

[57]WANG Yingchao,JING Hongwen,YU Liyuan,et al.Set pair analysis for risk assessment of water inrush in karst tunnels[J].Bulletin of Engineering Geology and the Environment,2016,6:1-9.

[58]杨鑫,王莹,王龙,等.基于集对分析理论的云南省水资源承载力评估模型[J].水资源与水工程学报,2016,27(4):98-102.

[59]黄瑞,张防修.基于优化集对分析模型的水质综合评价方法[J].长江科学院院报,2016,33(5):6-10,17.

[60]沈俊源,吴凤平,于倩雯.基于模糊集对分析的最严格水安全综合评价[J].水资源与水工程学报,2016,27(2):92-97.

[61]曹永强,高璐,朱明明,等.水资源系统脆弱性的评价方法及其应用[J].人民黄河,2016,38(9):46-49,73.

[62]YUE Wencong,CAI Yanpeng,RONG Qiangqiang,et al.A hybrid life-cycle and fuzzy-set-pair analyses approach for comprehensively evaluating impacts of industrial wastewater under uncertainty[J].Journal of Cleaner Production,2014,80:57-68.

[63]YANG Fengguang,LIANG Yue,VIJAU P S,et al.Debris flow hazard assessment using set pair analysis models:take Beichuan County as an example[J].J Mt Sci,2014,11(4):1015-1022.

[64]叶章蕊,卢毅敏.组合权重模糊联系度模型在水质评价中的应用[J].长江科学院院报,2016,33(9):33-39.

[65]杨哲,杨侃,蒋立伟,等.引入SPA理论的灰色聚类河流健康评价耦合模型[J].水电能源科学,2016,34(8):1-5.

[66]ZOU Qiang,ZHOU Jianzhong,ZHOU Chao,et al.Comprehensive flood risk assessment based on set pair analysis-variable fuzzy sets model and fuzzy AHP[J].Stochastic Environmental Research and Risk Assessment,2013,27(2):525-546.

[67]JIN Juliang,WEI Yiming,ZOU Lele,et al.Forewarning of sustainable utilization of regional water resources:a model based on BP neural network and set pair analysis[J].Natural Hazards,2012,62(1):115-127.

[68]范荣亮,谢悦波,付鹏,等.基于属性测度——联系数的节水型生态城市的健康评价[J].水利学报,2009,40(12):1460-1466.

[69]韦美雁.一种基于最小偏差的联系数多属性决策方法[J].数学理论与应用,2016,36(1):118-124.

[70]吴征,吴凤平,沈俊源.基于集对分析法的水资源配置方案综合评价[J].灌溉排水学报,2016,35(12):73-79.

[71]唐言明,白夏,卜松,等.基于广义联系度函数的城市防洪标准方案优选模型[J].水利与建筑工程学报,2016,14(2):178-181,201.

[72]王伟,江军,吴晓晖,等.偏联系数在城市污水处理方案优选中的应用[J].中国给水排水,2010,26(1):90-92,95.

[73]HU Junhua,YANG Liu.Dynamic stochastic multi-criteria decision making method based on cumulative prospect theory and set pair analysis[J].Systems Engineering Procedia,2011,1:432-439.

[74]CAO Yongxi,ZHOU Huan,WANG Jianqiang.An approach to interval-valued intuitionistic stochastic multi-criteria decision-making using set pair analysis[J].Int J Mach Learn & Cyber,2016:1-12.

[75]KUMAR K,GARG H.TOPSIS method based on the connection number of set pair analysis under interval-valued intuitionistic fuzzy set environment[J].Comp Appl Math,2016:1-11.

[76]董增川,马红亮,王明昊,等.基于组合决策的黄河流域水量调度方案评价方法[J].水资源保护,2015,31(2):89-94.

[77]金菊良,魏一鸣,王文圣.基于集对分析的水资源相似预测模型[J].水力发电学报,2009,28(1):72-77.

[78]冯利华,张行才,龚建林.关于集对分析的水文水资源变化趋势的统计预测[J].水文,2004,24(2):11-14.

[79]徐源蔚,李祚泳,汪嘉杨.基于集对分析的相似模型在地下水位预测中的应用[J].水文,2015,35(6):6-10.

[80]吴新新.基于改进集对分析的新疆黄水沟年径流预测[J].水资源开发与管理,2016(1):65-67,72.

[81]张云云,朱家明.基于集对分析聚类法对中国未来生活用水量的预测[J].河北北方学院学报(自然科学版),2016,32(3):32-36.

[82]和蕊,原晨阳,杨思波,等.集对分析聚类预测法在城市生活需水量预测中的应用[J].水利科技与经济,2010,16(12):1324-1327.

[83]万星.水电科学中若干新方法应用研究[D].成都:四川大学,2006.

[84]汪哲荪,袁潇晨,金菊良,等.基于集对分析的年径流自组织预测模型[J].水利水运工程学报,2010(4):33-37.

[85]FENG L H,SANG G S,HONG W H.Statistical prediction of changes in water resources trends based on set pair analysis[J].Water Resources Management,2014,28(6):1703-1711.

[86]段先前,褚学伟,李博.基于集对分析的岩溶塌陷危险性预测评价[J].安全与环境学报,2016,16(4):72-76.

[87]张金萍,林小敏,徐波.北京市降雨量与参考作物腾发量多时间尺度的集对分析[J].华北水利水电大学学报(自然科学版),2016,37(4):54-58.

[88]李深奇,肖景西,覃光华,等.基于率定量化标准系数的SPA年径流预测[J].长江科学院院报,2016,33(1):6-9.

[89]卢家海.基于集对分析的径流组合预测模型[J].水利科技与经济,2016,22(11):1-4.

[90]郭彦,金菊良,梁忠民.基于集对分析的区域需水量组合预测模型[J].水利水电科技进展,2009,29(5):42-45,60.

[91]王文圣,向红莲,李跃清,等.基于集对分析的年径流丰枯分类新方法[J].四川大学学报(工程科学版),2008,40(5):1-6.

[92]王文圣,李跃清,金菊良.基于集对原理的水文相关分析[J].四川大学学报(工程科学版),2009,41(2):1-5.

[93]符秋菊,郭纯青,周蕊,等.集对分析在水文统计、分类及相似性分析中的应用[J].水电能源科学,2013,31(6):47-50.

[94]蒋尚明,金菊良,许浒,等.基于经验模态分解和集对分析的粮食单产波动影响分析[J].农业工程学报,2013,29(4):213-221.

[95]杨淇翔,张琼楠,张平,等.基于广义集对势的年径流丰枯分类模型及应用[J].水电能源科学,2016,34(5):1-4.

[96]温孟婵,邓健健,马钰其,等.基于加权模糊集对分析的年径流丰枯分类方法[J].农业与技术,2016,36(2):250-251.

[97]蒋尚明,金菊良,袁先江,等.基于近邻估计的年径流预测动态联系数回归模型[J].水利水电技术,2013,44(7):5-9.

[98]万晨,万伦来,金菊良.安徽省水资源-社会经济系统协同分析[J].人民黄河,2016,38(9):50-55,67.

[99]周戎星,潘争伟,吴成国,等.山东省用水量变化趋势分析及驱动因子分析[J].环境工程,2016,34(增刊1):837-840.

[100]吴开亚,金菊良,魏一鸣,等.基于指标体系的流域水安全诊断评价模型[J].中山大学学报(自然科学版),2008,47(4):105-113.

[101]李宜敏,罗爱民,吕凤虎,等.集对分析联系度聚类方法在信息分类中的应用[J].火力与指挥控制,2008,33(8):145-148.

[102]黄大荣,黄丽芬.基于集对分析联系数故障树的BA系统可靠性分析[J].计算机应用研究,2010,27(1):111-113.

[103]欧开灿,金子成.基于SPA的类比推理预测法[J].西南民族学院学报(自然科学版),1998,24(3):254-257.

[104]吴开亚,金菊良,魏一鸣.流域水安全预警评价的智能集成模型[J].水科学进展,2009,20(4):518-525.

[105]成科扬.基于集对分析的模糊逻辑及其推理方法研究[C]∥程代展,王行愚.第二十三届中国控制会议论文集.上海:华东理工大学出版社,2004.

[106]马守明,王汝传,叶宁.基于集对分析的上下文感知不确定性的推理方法[J].南京邮电大学学报(自然科学版),2009,29(1):64-67.

[107]蒋云良.基于SPA联系数的同异反定量推理路径选择[J].微电子学与计算机,2000,17(5):6-9.

[108]陈悦莲.集对分析推理评优应用[J].甘肃联合大学学报(自然科学版),2006,20(5):46-48.

[109]杨亚锋.基于集对逻辑的近似推理方法研究[J].智能系统学报,2015,10(6):921-926.

[110]孙杰.基于集对推理的格序决策及应用[D].唐山:华北理工大学,2015.

[111]王会芳.基于集对分析的本体案例推理模型及应用[D].唐山:华北理工大学,2015.

[112]李丽红,杨亚锋,李言,等.集对推理与决策[M].北京:清华大学出版社,2016.

[113]刘秀梅,赵克勤.区间数决策集对分析[M].北京:科学出版社,2014.

(责任编辑：乔翠平)

Advances in Theoretical and Applied Research on Set Pair Analysis Method for Water Resources System

JIN Juliang1,2, SHEN Shixing1,2, PAN Zhengwei3, WANG Mingwu1,2, CUI Yi4

(1.School of Civil Engineering, Hefei University of Technology, Hefei 230009, China; 2.Institute of Water Resources and Environmental Systems Engineering, Hefei University of Technology, Hefei 230009, China; 3.School of Civil Engineering and Environmental Engineering, Anhui Xinhua University, Hefei 230088, China; 4.State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China)

Set pair analysis (SPA) is a novel intelligent computing theory and method which describes and processes uncertainty problems of system by means of the structural connection number. Due to its obvious characteristics of dealing with uncertainty problems, SPA has been widely used in many disciplines. There are many kinds of uncertainty in water resources system, such as randomness, fuzziness and so on. Therefore, SPA is an ideal system analysis method in dealing with problems of certain-uncertain water resources system. The advances are summarized in theoretical and applied research on set pair analysis method for water resources and the results show that the constitutional formula of connection number is a theory innovation, however, the uncertainty of difference degree coefficient gives rise to the uncertainty and complexity on the operation of connection number, which has limited the establishment and development of set pair analysis theoretical system. Therefore, it is necessary to strengthen study on theoretical foundation research of set pair analysis method for water resources system, and to continually deepen, expand and perfect the theory system of set pair analysis.

set pair analysis method for water resources system; connection number; difference degree coefficient; water resources evaluation; water resources decision; water resources forecast

2017-02-12

国家自然科学基金项目(51579059，51479045);国家重点研发计划项目(2016YFC0401303)。

金菊良(1966—)，男，江苏吴江人，教授，博导，博士，从事水资源系统工程方面的研究。E-mail:JINJL66@126.com。

10.3969/j.issn.1002-5634.2017.04.008

TV213

A

1002-5634(2017)04-0054-13