单变量独立同分布水文事件重现期的计算原理与方法
宋松柏, 金菊良
(1.西北农林科技大学 水利与建筑工程学院,陕西 杨陵 712100; 2.合肥工业大学 土木与水利工程学院,安徽 合肥230009)
单变量独立同分布水文事件重现期的计算原理与方法
宋松柏1, 金菊良2
(1.西北农林科技大学 水利与建筑工程学院,陕西 杨陵 712100; 2.合肥工业大学 土木与水利工程学院,安徽 合肥230009)
研究了单变量独立同分布水文事件的重现期的计算原理与方法。根据事件首次发生的期望等待试验次数与连续两次事件间期望间隔试验次数的两种重现期定义,采用数学期望值和概率母函数法,系统地推导了独立同分布水文事件重现期的计算公式。结果表明,单变量独立同分布水文事件在两种定义下的重现期相等。所得计算公式具有严格的数学基础,以期为我国现行水文频率的计算提供理论支撑。
水文事件;重现期;单变量;独立同分布
重现期是水利水电工程、土木工程等在规划设计、运行与管理中广泛采用的设计标准,主要根据工程的重要性和水文事件对工程的破坏结果进行确定[1-2]。在工程设计中,重现期有两种定义:①重现期(Return Period)是指超越概率事件首次发生的期望等待试验次数[3-4],如第一次发生大于等于某一设计值洪水的期望等待年数;②重现期(Interarrival time,Recurrence interval)表示连续两次超越概率事件发生之间的期望间隔试验次数(间隔时间)[4-6]。对水文频率的分析历经了百年的研究和应用历史,对重现期和相应设计值的计算[7-19],从单变量发展到多变量,从一致性事件发展到非一致性事件,为确定工程规模和工程管理提供了依据。
20世纪30年代后,我国开始引进和应用水文统计理论,经过几代水文科学工作者的不懈努力,为我国水利水电工程和土木工程的建设和管理提供了坚实的支撑。目前,国内外许多文献和教科书都介绍了单变量独立同分布水文事件重现期的第二种定义和计算公式,但都缺乏系统的理论推导介绍和总结。
本文在吸收国外学者研究成果的基础上,应用水文统计学原理和概率论原理,严格推导了单变量独立同分布水文事件的两种重现期定义的计算公式,以期为我国现行水文频率的计算提供严密的理论基础。
1 基于事件首次发生的期望等待试验次数确定重现期
假定水文随机变量X具有独立伯努利试验结果,满足独立同分布条件。设超越概率事件{X≥x}和不超越概率事件{X p=P(X≥x), q=P(X 下文中均与此假定及符号的物理意义相同。按事件首次发生的期望等待试验次数计算,其重现期为T(N)。 1.1 超越概率事件{X≥x}的重现期 设超越概率事件{X≥x}首次发生的等待试验次数为随机变量N。在n次试验中,前n-1次试验发生不超越概率事件{X P(N=n)=P(X1 P(X1 (1-p)n-1p。 (1) 式(1)表明,超越概率事件{X≥x}首次发生的期望等待试验次数服从几何分布。因此,超越概率事件{X≥x}首次发生的期望等待试验次数的数学期望值即为重现期T(N)。根据数学期望的定义和级数原理有 (2) 式(2)表明,超越概率事件{X≥x}的重现期等于其发生概率的倒数。 1.2 不超越概率事件{X 与超越概率事件{X≥x}重现期的计算相同,在n次试验中,前n-1次试验发生超越概率事件{X≥x},第n次试验发生不超越概率事件{X P(N=n)=P(X1≥x,X2≥x,…,Xn-1≥x,Xn P(X1≥x)·P(X2≥x)·…·P(Xn-1≥x)·P(Xn pn-1(1-p)。 (3) 式(3)表明,不超越概率事件{X (4) 式(4)表明,不超越概率事件{X 设连续两次超越概率事件{X≥x}发生的间隔试验次数为随机变量M,按事件连续两次发生的期望间隔试验次数计算,其重现期为T(M)。 2.1 超越概率事件{X≥x}的重现期 在试验中,首先发生超越概率事件{X≥x},紧接着连续发生m-1次不超越概率事件{X P(M=m)=P(Xi≥x,Xi+1 Xi+m-1 P(Xi≥x)·P(Xi+1 P(Xi+m-1 (5) 与式(2)的推导相同,有重现期 (6) 式(2)与式(6)表明,在独立同分布条件下,超越概率事件{X≥x}重现期的两种定义计算公式相同。 2.2 不超越概率事件{X 与超越概率事件{X≥x}重现期的推导相同,在试验中,首先发生不超越概率事件{X P(M=m)=P(Xi Xi+2≥x,…,Xi+m-1≥x,Xi+m P(Xi P(Xi+m-1≥x)·P(Xi+m (7) 与式(6)的推导相同,有重现期 (8) 式(4)与式(8)同样表明,在独立同分布条件下,不超越概率事件{X 3.1 概率母函数法 概率母函数(Probability Generating Function)定义为: (9) 概率母函数所具有的性质: G(0)=P(X=0); (10) (11) (12) G″(1)+G′(1)-[G′(1)]2=D(X)。 (13) 超越概率事件{X≥x}首次发生的等待试验次数概率母函数为: (14) (15) 则有 (16) 同理,对于不超越概率事件{X (17) 式(16)—(17)与文献[16]的结果相同。 采用同样的方法可得基于连续两次事件发生之间的期望间隔试验次数的重现期。 3.2 期望值推理法 对于容量为N的单变量事件,其平均长度E(l)=1,则单变量事件发生总次数的期望值E(C)为: (18) 设超越概率事件{X≥x}发生次数的期望值为E(Cr),根据概率原理有 (19) 则有 E(Cr)=pN。 (20) 根据重现期的涵义,有 (21) 同理,不超越概率事件{X (22) 本文在吸收国内外重现期研究成果的基础上,根据两种重现期定义,应用水文统计学原理和概率论原理,系统地推导了单变量独立同分布水文事件重现期的计算公式。结果表明,对于单变量独立同分布水文事件,基于事件首次发生期望等待试验次数与连续两次事件间期望间隔试验次数确定的重现期相等。另外,概率母函数法和期望值推理法推导的重现期也充分证明了单变量独立同分布水文事件重现期计算公式的正确性。 [1]金光炎.水文统计原理与方法[M].北京:中国工业出版社,1964. [2]黄振平,陈元芳.水文统计学[M].北京:中国水利水电出版社,2011. [3]STEDINGER J R,VOGEL R M,FOUFOULA G E.Frequency analysis of extreme events[M]∥Handbook of hydrology.New York:McGraw-Hill Book Company,1993:18.1-18.66. [4]CHUNG Chenhua,SALAS J D.Drought occurrence probabilities and risks of dependent hydrologic processes[J].Journal of Hydrologic Engineering,2000,5(3):259-267. [5]KITE G W.Frequency and Risk Analyses in Hydrology[M].Fort Collins,Colo:Water Resources Publications,1977. [6]LOAICIGA H A,MARINO M A.Recurrence interval of geophysical events[J].Journal Water Resources Planning and Management,1991,117(3):367-382. [7]FELLER W.An Introduction to Probability Theory and its Applications (Vol.(I)) [M].3rd Edition.New York:Wiley,1968. [8]SEN Zekai.Wet and dry periods of annual flow series[J]. Journal of the Hydraulics Division,1976,102(10):1503-1514. [9]CHOW V T,MAIDMENT D R,MAYS L W.Applied Hydrology[M].New York:McGraw-Hill Book Company,1988. [10]FERNANDEZ B,SALAS J D.Return period and risk of hydrologic event.I:mathematical formulation[J].Jounal of Hydrologic Engineering,1999,4(4):297-307. [11]FERNANDEZ B,SALAS J D.Return period and risk of hydrologic event.Ⅱ:applications[J].Journal of Hydrologic Engineering,1999,4(4):308-316. [12]BAYAZIT M.Discussion on “Return period and risk of hydrologic event.I:mathematical formulation”[J].Journal of Hydrologic Engineering,2001,6(4):358-363. [13]SHIAU J T.Return period of bivariate distributed extreme hydrological event[J].Stochastic Environmental Research and Risk Assessment,2003(17):42-57. [14]SALAS J D,OBEYSEKERA J.Revisiting the concepts of return period and risk for nonstationary hydrologic extreme event[J].Journal of Hydrologic Engineering,2014,19(3):554-568. [15]CANCELLIERE A,SALAS J D.Drought probabilities and return period for annual streamflows series[J].Journal of Hydrology,2010,391(1-2):77-89. [16]王正发.水文事件的频率、重现期和风险率之间的关系[J].西北水电,2000(1):1-3. [17]马秀峰,夏军.游程概率统计原理及其应用[M].北京:科学出版社,2011. [18]宋松柏,蔡焕杰,金菊良,等.Copulas 函数及其在水文中的应用[M].北京:科学出版社,2012. [19]史黎翔,宋松柏.具有趋势变异的非一致水文序列重现期计算研究[J].水力发电学报,2016,35(5):40-46. (责任编辑:陈海涛) Research on the Calculation Principle and Method of the Return Period of Univariate Independent and Identically Distributed Hydrological Event SONG Songbai1, JIN Juliang2 (1.College of Water Resource and Architectural Engineering, North West Agriculture and Forestry University, Yangling 712100, China; 2.School of Civil Engineering, Hefei University of Technology, Hefei 230009, China) The calculation principle and method of the return period of univariate and independent identically distributed hydrological event are presented. Based on two definitions of return period (the first occurrence expected waiting trials and expected interarrival trials between two consecutive events), used mathematical expectation and probability generating function, the return periods calculation formula of independent identically distributed event are derivated. The results show that the two definitions of return period have the same expression. These expressions have solid mathematical basis, and are expected to provide the theoretical bases for hydrological frequency analysis in China. hydrological event; return period; univariate event; independent and identically distribution 2017-06-19 国家自然科学基金项目(51479171,51579095,51179160)。 宋松柏(1965—),男,陕西永寿人,教授,博导,博士,从事水文学及水资源方面的研究。E-mail:ssbb533@nwsuaf.edu.cn。 金菊良(1966—),男,江苏苏州人,教授,博导,博士,从事水文学及水资源方面的研究。E-mail:JINJL66@126.com。 10.3969/j.issn.1002-5634.2017.04.006 TV12;P333.9 A 1002-5634(2017)04-0043-04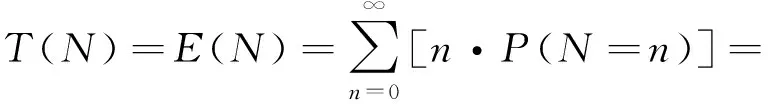

2 基于连续两次事件发生之间的期望间隔试验次数确定重现期
3 重现期的其他计算方法


4 结语

