哈尔滨地区汛期径流量变化趋势与复杂性分析

刘东, 程晨, KHAN Muhammad Imran, FAIZ Muhammad Abrar

(1.东北农业大学 水利与土木工程学院,黑龙江 哈尔滨 150030; 2.农业部农业水资源提高利用重点实验室,黑龙江 哈尔滨 150030; 3.黑龙江省粮食产能提升协同创新中心,黑龙江 哈尔滨 150030; 4.黑龙江省普通高校节水农业重点实验室,黑龙江 哈尔滨 150030)

哈尔滨地区汛期径流量变化趋势与复杂性分析

刘东1,2,3,4, 程晨1, KHAN Muhammad Imran1, FAIZ Muhammad Abrar1

(1.东北农业大学 水利与土木工程学院,黑龙江 哈尔滨 150030; 2.农业部农业水资源提高利用重点实验室,黑龙江 哈尔滨 150030; 3.黑龙江省粮食产能提升协同创新中心,黑龙江 哈尔滨 150030; 4.黑龙江省普通高校节水农业重点实验室,黑龙江 哈尔滨 150030)

区域水文要素复杂性研究是当今的热点问题,为了研究哈尔滨地区汛期径流量的复杂性特征及变化趋势,将R/S分析法和等概率粗粒化LZC算法引入到区域径流复杂性分析与变化趋势预测中,对地区内10个水文站点的汛期径流序列的复杂性进行诊断并对其变化趋势进行分析。研究结果表明:哈尔滨、通河、阿城、依兰、烟囱山各站未来的汛期径流量呈减少趋势，岔林河、莲花、西北河、延寿、四平山各站未来的汛期径流量呈增长趋势;各站点汛期径流序列的复杂度由高到低依次为:四平山、烟囱山、岔林河、阿城、西北河、依兰、莲花、通河、哈尔滨、延寿；从河流集水面积对其径流长程相关性和复杂性的影响可以看出,站点的河流集水面积越大,其径流量的长程相关性越强,复杂性指数越小。研究成果揭示了本地区汛期径流量的变化趋势以及复杂性演变特征,该特征可为区域径流预测及水资源优化配置提供科学依据。

R/S分析法;等概率粗粒化LZC算法;哈尔滨地区;汛期径流量；变化趋势；复杂性

水资源是人类赖以生存的基础,也是工、农业生产的重要影响因子,水资源量的充沛程度直接决定了人类的生活质量和社会的发展速度。水资源的演变过程具有复杂的线性、非线性特征,存在突变性、趋势性及多时间尺度等特性。哈尔滨市地处东北亚中心地带,水土资源丰富,是我国重要的商品粮生产基地。近年来,受全球气候变暖、流域内人口不断增加和水田面积迅速扩大的影响,致使哈尔滨地区的用水和供水矛盾日益突出。地表径流是各行业及城市供水的一个重要途径,因此,讨论哈尔滨地区汛期径流量的变化对工、农业及城市的发展具有十分重要的意义。

目前,关于水文要素复杂性的测度方法有很多,如分形理论[1]、网格法[2]、熵理论[3]、混沌理论[4]等。这些方法在一定程度上都可以实现对系统复杂性的定量描述,但均存在局限性。在以往的研究中,有许多学者对哈尔滨地区的径流变化趋势及复杂性开展了研究,但大多是基于较少的水文站点和较短的时间序列,在大时间尺度下的研究很少。因此,本文基于哈尔滨地区1964—2010年10个水文站点的径流资料,采用R/S分析法和等概率粗粒化LZC算法对哈尔滨地区松花江及其各个支流的汛期径流量的变化趋势和复杂性进行计算分析,以期为哈尔滨地区松花江流域水资源的规划与管理提供依据。

1 研究方法

1.1 R/S分析法

R/S分析法是英国水文学家Hurst在1951年提出的一种用以分析时间序列的方法。R/S分析法对分形理论有着重要的作用,同时对时间序列有预测功能[5]。R/S分析法通常被用于计算分形理论中的赫斯特(Hurst)指数,进而用来分析时间序列的动态变化趋势。对于时间序列φ(t)(t=1,2,…,n),其时间跨度τ为正整数,且τ≥1,则在时间跨度τ内有均值序列〈φ〉τ,其表达式为:

(1)

进而可以计算出累计离差X(t,τ)，

(2)

在此基础上，标准差S(τ)和极差R(τ)可根据以下公式依次计算：

(3)

R(τ)=maxX(t,τ)-minX(t,τ)。

(4)

于是，Hurst指数可表示为：

(5)

式中:H为Hurst指数;c为常数。

对式(5)两边分别求自然对数,可得:

(6)

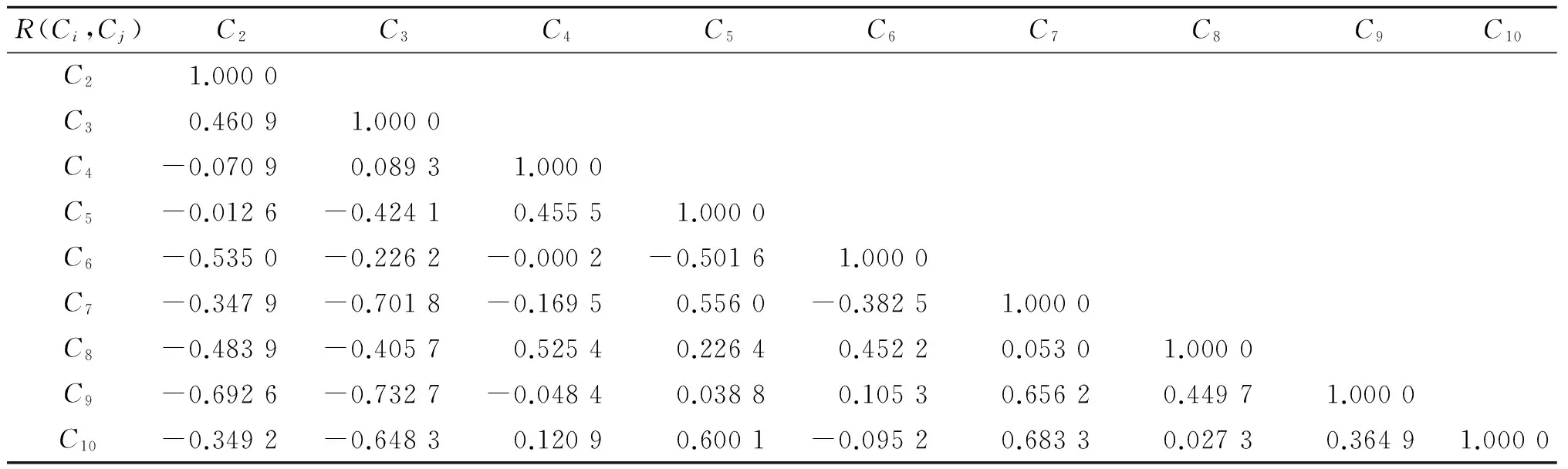
Hurst指数(0≤H≤1)为R/S分析法的一个有效统计量。Hurst指数能分析出时间序列中的趋势性,并且根据H值的大小可以判断出时间序列趋势性的强弱[6]。当0≤H<0.5时,表明该时间序列存在反持续性,即未来的变化趋势将与过去的总体变化趋势相反,且H值越趋近于0,反持续性越强;当H=0.5时,表示该时间序列为独立的随机序列,即未来的变化趋势与过去的总体变化趋势无关;当0.5

1.2 等概率粗粒化LZC算法

等概率粗粒化LZC算法是由A.Lempel和J．Ziv在1976年提出的一种复杂性诊断方法。 其核心理论是用相同长度的简单字符重构原时间序列[10],重构时间序列称为原序列的粗粒化序列。

对于某一给定的时间序列xt(t=1,2,…,n),定义字符集St为序列xt经l段粗粒化后所生成的字符串，

(7)

式中:Sj为两两互不相同的字符,j=1,2,…,l;xmax、xmin分别为序列xt的最大值和最小值;d=(xmax-xmin)/l。

由此建立一个具有l个不同字符的符号序列St。

考虑到以下两点原则:①字符Sj在重构序列中出现的频率应尽量相等；②原时间序列中的相等数据须在重构序列中对应相同的字符[12]。进而提出了等概率粗粒化方法，其具体算法如下:

对原序列xt从小至大排序,得xmin≤xk1≤xk2≤l≤xkn≤xmax,其中：k1,k2,…,kn为原序列中相应的序号。用fj(j=1,2,…,l)表示第j个分割点在重排序列中的序号,令:

(8)

式中tj为满足原则①的第j个分割点的序号。

排序后的序列里,若数值与xtj相等的数据有mj个时,为了满足原则②,则有:

(9)

当分割点序号fj全部确定后,设{S(kt)}为等概率粗粒化后的序列,将{S(kt)}赋值为:

(10)

等概率粗粒化方法中由于原则②的约束,所得tj对应的mj≠1,且tj或者当n无法被l整除时,字符S1,S2,…,Sl在{Sj}中出现的频率不会完全相同。但通过试验研究发现,若非线性时间序列n>>l时,会实现不同字符在重构序列中出现的概率相等或基本相等的情况。

A．Lempel和J．Ziv的研究成果表明:当n→∞时,随机序列的复杂度值趋近于定值n/logln,且归一化复杂度值可表示为:

(11)

式中c(n)为S(τ)中不同字符串的个数。

用归一化的信源熵N进行修正,则：

(12)

(13)

式中:Pj为各符号在字符串中出现的概率;CN为修正后的归一化复杂度值。

2 研究区域概况与数据描述

2.1 研究区域概况

哈尔滨市位于中国东北平原的东北部地区,是黑龙江省省会城市。地理坐标44°04′～46°40′ N, 125°42′～130°10′ E,总面积达53 840 km2，共有人口994万,是我国东北地区的政治、经济、文化中心。哈尔滨属于温带大陆性季风气候,冬季漫长,夏季短暂,农作物品质好、商品率高,是中国主要的粮食产区。哈尔滨的雨季在6—9月,雨季降水量占全年降水量的60%左右。区域内河水资源丰富,但分布不均,东部地区水资源相对充足,而西部地区则相对匮乏,河流汛期为每年的7—9月[13]。近些年来,工业的发展导致哈尔滨地区河水污染严重,几乎无法使用,同时,水田的大面积种植使得农业用水量急剧增加。以上种种原因导致了哈尔滨地区的水资源供需极不平衡[14],解决用水矛盾已成为一个迫在眉睫的问题。

2.2 数据描述

本文数据来源于哈尔滨市水文局提供的1964—2010年10个水文站点(哈尔滨、通河、依兰、阿城、岔林河、西北河、烟囱山、四平山、延寿、莲花)的逐月径流资料。绘制各水文站47 a间每年汛期(7—9月)径流量序列(n=141)的变化曲线,结果如图1所示。由图1可以看出,各站点汛期径流量序列都有着很明显的周期性波动,且除岔林河站表现出上升趋势外,其余站点均表现出下降趋势。

图1 哈尔滨地区汛期径流序列变化曲线

3 结果与分析

3.1 汛期径流序列的R/S分析结果

图2 哈尔滨地区汛期径流序列的R/S拟合结果

回归方程指标 哈尔滨通河依兰 阿城岔林河西北河烟囱山四平山延寿莲花常数-0.5826-0.24890.0614-0.1390-0.28290.41100.03020.48700.48690.2629H值0.92980.74460.63830.69700.78120.39910.57030.32700.32670.4407R2值0.89760.89450.89610.89180.96740.86230.92360.83900.83880.8889

由表1可以看出：有6个站点的汛期径流量H值大于0.5,由高到低依次为:哈尔滨(0.929 8)、岔林河(0.781 2)、通河(0.744 6)、阿城(0.697 0)、依兰(0.638 3)、烟囱山(0.570 3),根据Hurst指数的内涵可知,这6个站点的汛期径流量序列都具有长程相关性[15]，即未来的发展变化趋势将与过去的多年总体变化趋势相同，且哈尔滨站的H值最大,说明哈尔滨站径流量的未来变化趋势的持续性最强；其余4个站点的汛期径流量H值小于0.5,由高到低依次为:莲花(0.440 7)、西北河(0.399 1)、四平山(0.327 0)、延寿(0.326 7),说明这4个站点的汛期径流序列表现出反持续性,即未来的变化趋势将与过去的多年总体变化趋势相反[17]。结合各站点的Hurst指数值以及图1趋势线可以判断出各站点未来汛期径流量的变化趋势,具体表现为:四平山、延寿、莲花、岔林河、西北河各站汛期径流量呈增长态势,哈尔滨、阿城、通河、依兰、烟囱山各站汛期径流量呈减少态势。

3.2 汛期径流的复杂度分析

等概率粗粒化LZC算法的主要目标是求解粗粒化段数问题,传统二值粗粒化方法会忽略序列内部的重要信息,而等概率粗粒化方法解决了这些问题,提高了分析精度。本文取粗粒化段数l=2、3、4、5、6、7、8、9、10,运用上述等概率粗粒化LZC算法分别计算哈尔滨地区10个站点的汛期径流序列归一化复杂度值,计算结果见表2。各站点汛期径流序列归一化复杂度值随粗粒化段数变化的关系如图3所示。由表2和图3可以发现,伴随着粗粒化段数的增加,各站点汛期径流序列都出现了复杂度值交替波动的特征。

表2 不同粗粒化段数下哈尔滨地区各站点汛期径流序列归一化复杂度值

图3 各站点汛期径流序列归一化复杂度值随粗粒化段数变化的关系

为了验证不同分段数下复杂度值的稳定性,计算各粗粒化段数下复杂度之间的相关系数。显然,相关系数越大,其所对应的粗粒化段数越合理,计算的复杂度值在表征序列复杂性时的稳定性就越好[17]。分别计算分段数为i、j(i、j=2、3、4、5、6、7、8、9、10,且i≠j)时所对应的复杂度序列Ci和Cj之间的相关系数R(Ci,Cj),计算结果见表3。由表3可知，R(Ci,Cj)max=R(C7,C10)=0.683 0,由此说明,C7和C10是反映哈尔滨地区各站点汛期径流序列复杂性的最优值。因此,取C7和C10的平均值作为哈尔滨地区汛期径流序列复杂性测度的最终结果,详见表4。

表3 不同粗粒化段数下复杂度值之间的相关系数值

表4 哈尔滨地区各站点汛期径流序列复杂性排序

由表4可知,哈尔滨地区各站点汛期径流序列的复杂性综合排序由高到低依次为:四平山、烟囱山、岔林河、阿城、西北河、依兰、莲花、通河、哈尔滨、延寿。

根据等概率粗粒化LZC算法的原理可知,最终求归一化复杂度时存在假设“当n→∞时,随机序列复杂性测度值趋于定值n/logln[18]”,而本文采用的时间序列长度为141,序列长度偏短。因此，在计算过程中出现了大于1的异常值，但相关系数计算中最终获得的稳定性最好的复杂度为C7和C10,两者均为小于1的正常值,因此，这些异常值不影响本文最终的复杂度计算结果。

3.3 集水面积与Hurst指数和LZC复杂度分析

通过获得的各站点所在位置的河流集水面积,对比河流集水面积与Hurst指数和LZC复杂度，结果如图4所示。

由图4可以看出：Hurst指数大于0.5的多为集水面积较大的站点,Hurst指数小于0.5的多为集水面积较小的站点。从而说明,集水面积越大，河流径流量的长程相关性越强；当河流集水面积很小时,径流量受外界小区域短时因子的影响很大。因此，长程相关性很弱或呈现出随机游走的状态。对照等概率粗粒化LZC算法计算的复杂度结果可以发现,复杂度大的多为集水面积小的站点；而集水面积大的站点，其复杂度均相对较小。由此分析可知,径流序列复杂度指数的大小不仅与降水等因素有关,还与河流集水面积有关,集水面积越大,复杂度越小。从实际情况来看,河流集水面积越小，外界因素对其径流量的影响就越明显,比如短时干旱、人类灌溉用水等因素；而当河流集水面积很大时,比如松花江,它的径流量变化更多是受自然环境年际变化的影响,小范围的人类活动或小区域短时气候变化对其径流量的影响较小。

图4 哈尔滨地区各站点河流集水面积、Hurst指数及LZC复杂度对照图

4 结语

本文将R/S分析法和等概率粗粒化LZC算法运用于哈尔滨地区汛期径流序列的变化趋势分析和复杂性分析中，结果稳定可靠且易于实现,得出以下主要结论。

1)R/S分析结果表明:四平山、延寿、莲花、岔林河、西北河各站汛期径流量呈现增长态势,哈尔滨、阿城、通河、依兰、烟囱山各站汛期径流量呈现减少态势。

2)通过等概率粗粒化LZC算法结果可以看出，哈尔滨地区各站点汛期径流序列的复杂性存在显著区别,由高到低依次为:四平山、烟囱山、岔林河、阿城、西北河、依兰、莲花、通河、哈尔滨、延寿。

3)通过对比各站点河流的集水面积,总结了河流集水面积对其径流长程相关性和复杂性的影响,具体表现为：河流集水面积越大,其径流量的长程相关性越强,复杂性指数越小。

本文成果为研究区域水文过程变化的复杂性提出了一个新思路,可为进一步完成哈尔滨地区水资源优化配置提供科学保障。同时,也可为今后哈尔滨地区的汛期径流量预测提供科学依据。

[1]张少文,王文圣,丁晶,等.分形理论在水文水资源中的应用[J].水科学进展,2005,16(1):141-146.

[2]余姝萍,刘国东,吴媛,等.岷江上游日径流过程分维分析及其生态脆弱性表征[J].西南民族学学学报(自然科学版),2005,31(1):79-84.

[3]李华晔,黄志全,姜彤.河流水系分形分初步研究[J].华北水利水电学院学报,1998,19(4):36-38.

[4]王志良,张永山.昆明年降雨量时间序列的混沌分析[J].华北水利水电学院学报,2011,32(2):8-10.

[5]MATOS J M O,MOURA E P D,KRUGER S E,et al.Rescaled range analysis and detrended fluctuation analysis study of cast irons ultrasonic backscattered signals[J].Chaos,Solitons & Fractals,2004,19(1):55-60.

[6]KIKUCHI R,TSUTSUMI A.Characterization of nonlinear dynamics in a circulating fluidized bed by rescaled range analysis and short-term predictability analysis[J].Chemical Engineering Science,2001,56(23):6545-6552.

[7]GAMMEL B M.Hurst′s rescaled range statistical analysis for pseudorandom number generators used in physical simulations[J].Physical Review E,1998,58(2):2586-2597.

[8]HORVATH,SCHILLER R.Rescaled range analysis of the corrosion potential noise[J].Corrosion Science,2003,45(3):597-609.

[9]MIRANDA J G V,ANDRDE R F S.Rescaled range analysis of pluviometric records in Northeast Brazil[J].Theoretical and Applied Climatology,1999,63(1):79-88.

[10]刘峰涛,贺国光.基于L-Z方法的宏观交通运输系统复杂性测度[J].哈尔滨工业大学学报,2008,40(12):2058-2061.

[11]武秋晨,刘东.等概率粗粒化LZC算法在降水变化复杂性研究中的应用[J].中国农村水利水电,2013(5):1-5，10.

[12]张佃中,谭小红,王智,等.基于等概率粗粒化的复杂度算法及其应用[J].系统仿真学报,2008,20(15):4096-4098，4103.

[13]何宇,吴艳春,田志成.哈尔滨市水资源量分析[J].水利科技与经济,2009,15(2):154-155.

[14]刘百仓,马军,余海艳,等.哈尔滨市水资源开发利用现状及其可持续发展战略研究[J].水利学报,2007,38(增刊1):482-484.

[15]康超冯,刚段延,宾邱林.R/S分析在水库径流丰枯变化趋势预测中的应用[J].华北水利水电学院学报,2008,29(5):7-9，11.

[16]张鑫,蔡焕杰,尹晓楠.应用重标度极差分析法(R/S)分析无定河流域水沙变化[J].农业工程学报,2010,26(增刊2):212-217.

[17]DANIEL A,ROBERTO H,CARLOS G,et al.Analysis of EEG background activity in Alzheimer′s disease patients with Lempel-Ziv complexity and central tendency measure[J].Medical Engineering & Physics,2005,28(4):315-322.

[18]张佃中.非线性时间序列互信息与Lempel-Ziv复杂度的相关性研究[J].物理学报,2007,56(6):3152-3157.

(责任编辑：张陵)

Analysis on Variation Trend and Complexity of Runoff in Flood Season in Harbin Area

LIU Dong1,2,3,4, CHENG Chen1, KHAN Muhammad Imran1, FAIZ Muhammad Abrar1

(1.School of Water Conservancy & Civil Engineering, Northeast Agricultural University, Harbin 150030, China; 2.Key Laboratory of Effective Utilization of Agricultural Water Resources of Ministry of Agriculture, Northeast Agricultural University, Harbin 150030, China; 3.Heilongjiang Provincial Collaborative Innovation Center of Grain Production Capacity Improvement, Northeast Agricultural University, Harbin 150030, China; 4.Key Laboratory of Water-Saving Agriculture of Ordinary University in Heilongjiang Province, Northeast Agricultural University, Harbin 150030, China)

Regional hydrological complexity is a hot issue today, in order to analyze the variation trend and complexity of the runoff in flood season in Harbin area, in this paper, R/S analysis method and equal probability coarse graining LZC algorithm were introduced into the analysis of regional runoff complexity and the forecast for the variation trend of regional runoff. Taking Harbin region as an example, the complexity of the runoff sequences from ten hydrological stations in flood season in this region was diagnosed, and the variation trend of the runoff sequences was analyzed. The results show that for the trend of the runoff in future flood reason, those from the hydrological station of Harbin, Tonghe, Acheng, Yilan and Yancongshan will increase, those from the hydrological station of Chalinghe, Lianhua, Xibeihe, Yanshou and Sipingshan will decrease. The high-to-low order of the complexity of the runoff sequences of hydrological stations in flood season is Sipingshan station, Xibeihe station, Chalinghe station, Acheng station, Lianhua station, Yilan station, Yancongshan station, Tonghe station, Harbin station, Yanshou station. This paper summarizes the influence of river′s catchment area on the long-range correlation and complexity of runoff, that is, the larger the catchment area, the stronger the long-range correlation of the runoff, and the smaller the complexity index. The research results reveal the variation trend of runoff volume and evolution characteristics of its complexity of the region in flood season, and which will provide scientific basis for regional runoff forecast and water resources optimal allocation.

R/S analysis method; equal probability coarse graining; LZC algorithm; Harbin area; the runoff in flood season; the variation trend; complexity

2016-11-28

国家自然科学基金项目(51579044,41071053,51479032);哈尔滨市创新人才研究专项资金项目(优秀学科带头人)(2013RFXXJ001);黑龙江省水利科技项目资助(201319,201501,201503)。

刘东(1972—),男,黑龙江安达人,教授,博导,博士,从事水资源优化利用与管理方面的研究。E-mail:liudong5511@sina.com

10.3969/j.issn.1002-5634.2017.04.001

TV121

A

1002-5634(2017)04-0001-08