基于指标规范化的正态云模型的水安全评价

周云哲, 粟晓玲

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

基于指标规范化的正态云模型的水安全评价

周云哲, 粟晓玲

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

针对传统评价方法没有同时兼顾评价指标的不确定性和模糊性问题，引入正态云模型对水安全状况进行定量评价。为克服正态云模型评价无法规范地体现不确定性的问题，运用指标规范化变换统一正态云模型中超熵的取值，使正态云模型评价规范化。以甘肃省河西走廊黑河中游地区为例进行了水安全评价研究。评价结果表明：2005—2011年，黑河中游地区水安全状态由不安全级别提升至临界级别；2011—2015年间，水安全状态基本稳定且有变好趋势，但工业用水重复利用率、土壤盐渍化率、森林覆盖率、水利投资占GDP的比例等指标处于危险级别或不安全级别，采取有效的管控手段是当前该区域水安全建设的重点。

水安全评价；正态云模型；指标规范化；黑河中游

水是生命之源，生态之基，生产之要[1]。20世纪以来，随着社会经济的发展，需水量增加导致严重的水供需矛盾，许多地区的水资源开发利用超过了水资源的承载能力，危及自然和社会经济系统的正常运转，引发水安全问题。水安全问题包括水资源短缺、水灾害引起的水量问题及水体污染导致的水质问题等，涵盖了资源、环境、生态、社会、政治等多个方面[2-4]。韩宇平等[5]认为，水安全是指在现在或将来由于自然的水文循环波动或人类对水循环平衡的不合理改变，或是二者的耦合，使得人类赖以生存的区域水状况发生对人类不利的演进，并正在或将要对人类社会的各个方面产生不利的影响，表现为干旱、洪涝、水量短缺、水质污染、水环境破坏等，并由此可能引发粮食减产、社会不稳、经济下滑及地区冲突等。

由于社会至今没有对水安全有一个公认的定义，水安全评价指标体系与评价模型也不尽相同。英国生态与水文中心提出由资源(Resource)、途径(Access)、利用(Use)、能力(Capacity)和环境(Environment)5个分指数组成的水贫困指数(Water Poverty Index，WPI)[6]，用于反映水资源短缺对人类的影响；曾畅云等[7]运用压力-状态-响应(PSR)概念模型从社会经济、生态环境、水环境 3 个方面建立了水环境安全评价指标体系，应用综合指数法对北京市水环境安全进行了综合评价；施春红等[8]运用多元分析和因子分析法对我国主要城市的供水安全进行了评价分析；金菊良等[9]利用信息熵确定指标权重，提出了基于智能算法的模糊层次分析法评价我国7省区的水安全形势；吴开亚等[10]用集对分析方法构造可变模糊集的相对隶属度函数，进而利用模糊综合评价方法建立了水资源安全定量评价模型，对巢湖流域水资源安全状况进行评价；李祚泳等[11]对水安全评价指标进行适当变换，采用普适指数公式对山东省水安全进行评价，结果表明，普适指数公式评价方法具有计算简便、普适通用的特点。此外，还有物元评价法[12]、属性识别评价法[13]、支持向量机评价模型[14]和投影寻踪评价模型[15]等被用于水安全评价。

李德毅院士于20世纪90年代提出了一种基于模糊数学和概率论的不确定分析方法——云模型[16]，云模型兼顾随机性和模糊性，实现了由定量评价向定性评价的转换，克服了传统评价方法在考虑模糊性和随机性方面的不足[17]。目前，云模型在土地利用评价[18]、大坝安全评价[19]、电能质量评价[20]、生态风险综合评价[21]、地震灾害风险综合评价[22]等领域被广泛应用。在运用正态云模型评价水安全状况的实例中，不同数量级指标在云模型中的超熵值He差别很大，无法规范地体现其不确定性。针对这一问题，本文借鉴物理学中普遍存在的规范不变性原理，将不同指标的同级标准值进行规范化变换[23]，将不同数量级的评价指标规范为同一数量级的评价指标，然后进行正态云模型综合评价，统一各指标等级正态云模型中的超熵值He，克服不同数量级指标无法规范地体现不确定性的问题，结合熵权法确定指标权重，建立黑河中游地区水安全状况综合评价模型，对2005年和2011—2015年水安全状况进行综合评价。

1 研究区域概况

黑河是我国西北地区第二大内陆河，发源于青海省祁连山，流经青海、甘肃、内蒙古。黑河流域气候属典型大陆性气候，蒸发量大，降水量小，且水量年内分配极不均匀。黑河流域面积14.29万km2。黑河中游地区位于莺落峡断面至正义峡断面之间，行政区包括山丹、民乐、张掖、临泽、高台、肃南、酒泉等市县，地处古丝绸之路要地，拥有悠久的农牧业开发历史，是甘肃省粮食基地，战略地位十分重要。中游地区的张掖市是流域内工农业较为发达的地区，属灌溉农业经济区，农业用水占总用水的80%以上，水资源利用程度高，利用量大。建国以来，大规模水土资源开发和经济社会的快速发展，流域生态环境体系不断恶化，水安全问题日益突出。近10年来，该区域水安全问题得到重视，通过加大投入、综合治理和科学发展，该地区农业、产业现代化水平明显提高，2005年以来，粮食产量不断增长，人均纯收入大幅提高，生态环境逐步向良好方向发展，水安全问题趋于缓和。但水安全问题仍是该地区突出问题之一，水资源短缺依然是制约该地区发展的重要因素，开展黑河中游地区的水安全评价研究，可为区域水资源合理利用及生态环境建设提供依据。

2 水安全评价方法

2.1 正态云模型简介

设U是一个精确数值表示的定量论域，C是U上的定性概念，若定量值x∈U，且x是定性概念C的一次随机实现，x对C的确定度μ(x)∈[0,1]是有稳定倾向的随机数[16]：

μ:U→[0,1] ， ∀x∈U，x→μ(x)。

则x在论域U上的分布称为云(Cloud)，每一个(xi,μi)称为一个云滴。云用期望Ex、熵En和超熵He3个数字特征来整体表征1个概念;Ex是云滴在论域空间分布的期望；En是对定性概念的不确定性度量，由概念的随机性和模糊性共同决定；超熵He是熵的不确定性的度量，即熵En的熵，由熵的随机性和模糊性共同决定，反映了云滴的离散程度。正态分布是概率理论的重要分布之一，用均值和方差两个数字特征表示。数字特征期望Ex和熵En的计算方法[19]分别如下：

(1)

(2)

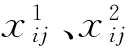
本文通过正态云发生器实现x→μ(x)转换，步骤[16]如下：

步骤3 求解确定度μi:

(3)

步骤4 循环步骤1—3N次，得到各个云滴(xi,μi)组成云像。

超熵He根据评价指标等级标准的实际情况进行取值。本文中对指标等级阈值变换后的规范值变化范围是[0.1,0.7]，为规范地表达不确定性评价，各指标构成的正态云模型超熵值统一取为0.005。

2.2 水安全评价指标体系构建

目前，水安全评价指标没有明确的统一标准，区域水安全评价中的评价因子之间具有复杂的联系。因此，本研究根据综合评价遵循的层次性、完备性、可操作性等原则，考虑黑河中游地区水安全状况实际水平，参考我国西北内陆干旱区标准和国内平均值及相应的研究成果，结合专家讨论意见，根据黑河中游地区水资源、水生态环境现状和特征，从水安全的生命安全、社会经济安全、生态安全、管理安全4个方面建立了由17个指标构成的水安全评价指标体系，确定了评价指标的等级划分。指标体系及等级划分结果见表1。

表1 水安全评价指标体系及评价等级

注：“—”表示无量纲。

水安全评价中的评价指标分为正向指标和负向指标两类。正向指标中，人均水资源量(C1)、人均生活用水定额(C2)、饮用水水质达标率(C3)、人均粮食占有量(C7)、森林覆盖率(C15)的值越大，表示区域水安全基本状态越好；工业用水重复利用率(C6)、有效灌溉面积率(C8)、农民人均纯收入(C10)、废污水处理达标率(C12)、生态环境用水率(C14)、水利投资占GDP的比例(C16)、灌溉水利用系数(C17)的值越大，表示区域水资源承载能力和抵御外界灾害冲击的能力越强，也反映出对区域水安全问题的重视程度和解决问题的投入越大。负向指标中，干旱指数(C4)、土壤盐渍化率(C13)的值越大，表示区域水生态环境状况越差，水安全问题越突出；工业万元产值用水量(C5)、人口自然增长率(C9)、干旱受灾面积率(C11)的值越大，表示区域水资源利用水平越低，水资源的水生态承载压力越大，外界对区域水安全状况冲击的损毁度越高，表明区域水安全状况越差。

选用熵权法确定评价指标的权重向量W。熵权法的基本步骤如下[19]：

步骤1 设每一个指标有m个实际观测值，xij表示第i个评价指标的第j个观测值。评价指标矩阵为：

X=[xij]m×n，

将矩阵X归一化处理，得到标准矩阵Y，

Y=[yij]m×n。

步骤2 计算第i项评价指标的熵ei，

(4)

其中k=lnn。

步骤3 计算各评价指标权重wi，

(5)

(6)

评价指标客观权重矩阵为：

W={w1,w2,…,wn}。

各指标权重见表1。

2.3 基于指标规范化的正态云模型的水安全综合评价

区域水安全评价指标的定量描述具有模糊性和随机性，以往的模糊评价和综合指数评价模型对于同时考虑评价对象的模糊性与随机性能力尚有不足。本研究引入正态云模型，以正态云模型理论为基础构建黑河中游地区水安全综合评价模型，主要步骤如下：

步骤1 建立黑河中游地区的水安全评价指标阈C，

C={c1,c2,…,c17}，

水安全指标标准阈S，

S={s1,s2,…,s17}，

权重向量W，

W={w1,w2,…,w17}。

步骤2 确定各指标云模型数字特征，运用正态云发生器绘出云像图，对评价体系中各实测值进行评估计算，得到实测值对应的隶属度向量矩阵，

Z=(zij)17×5，

其中元素zij表示评价指标阈C中第i个元素ci对于指标标准阈S中的第j个等级sj的隶属度，即：

zi=(d1,d2,d3,d4,d5)。

(7)

为提高水安全评价结果的置信度，需要多次执行正态云发生器，之后对zi取算术平均值确定dj并进行标准化，

(8)

(9)

F=(f1,f2,f3,f4,f5)。

(10)

取加权平均值即可得到水安全评价各个指标的评分vi，

(11)

步骤3 结合评价年17个评价指标实测值的评分构成的指标评分集合向量

V={v1,v2,…,v17}，

与权重向量

W={w1,w2,…,w17}，

经加权计算，得到评价年的水安全综合分值v综合，

v综合=VWT。

(12)

以分值v综合对应的水安全等级作为评价结果。

图1 水安全评价等级分值评判的正态云模型

在上述评价隶属度向量矩阵确定过程中，超熵He的取值随着指标标准阈值的数量级的不同而变化，不具有一致性。较大数量级且等级阈值范围大的指标的云模型数字特征会使云滴以正态分布的形式汇集成一条极为近似的正态曲线，变为钟型隶属函数图形，无法体现评价的不确定性，因此需要将各指标等级标准进行规范变换。而普通的线性归一化不具有普适性，这里采用设定“参照值”ci0，将各同级指标标准阈值进行规定的指数变换，较好地保留各等级标准阈值的数字特征，并在正态云模型应用中保留了大数量级指标评价的不确定性。

从表1中可以看出，水安全评价指标的单位量纲不相同，不同指标的同级标准值有的相差几个数量级，故需先对各评价等级标准值与评价年指标实测值进行规范变换，再将变换结果运用于正态云模型评价中。通过不同的规范函数表达式和选定的“参照值”ci0规范变换，得到同一级标准的不同指标的规范函数xik(i代表指标，k代表等级)[23-25]。

1)对于正向指标(C1、C2、C6、C7、C8、C10、C12、C14、C15、C16、C17)采用的变换函数为：

xik=(ci/ci0)ni。

(13)

2)对于逆向指标(C4、C5、C9、C11、C13)采用的变换函数为：

xik=(ci0/ci)ni。

(14)

3)对于等级标准值彼此接近的正向指标(C3)采用的变换函数为：

xik=(ci-cb/ci0)ni。

(15)

式中：cb的设置是为了扩大不同等级之间的差异，便于评价，本次评价取值cb=87；ni一般取0.5、1.0、2.0，根据等级标准值的数字特征确定，指标C1、C2、C6、C9、C10和C14的ni取为1.0，指标C3、C4、C5、C11和C13的ni取为0.5，指标C7、C8、C12、C15、C16和C17的ni取为2.0。

(16)

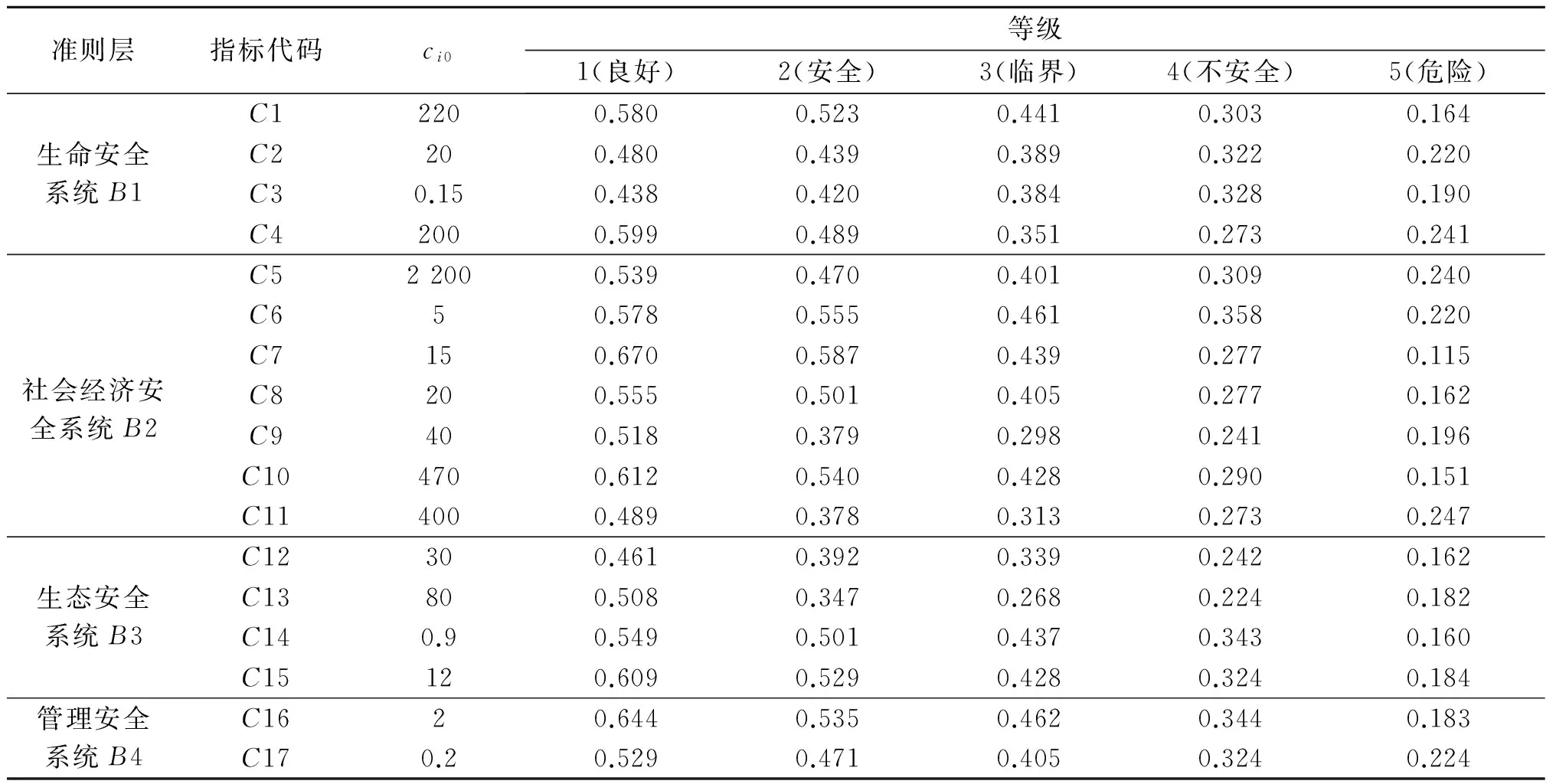
表2 水安全评价指标规范变换结果

3 水安全评价结果与分析

基于已经建立的区域水安全评价指标体系，通过规范变换后的正态云模型表示各评价指标对应的评价等级，超熵统一取值为0.005，计算过程由MATLAB软件编写模型运行程序进行。本次评价选取2005年和2011—2015年作为评价年，评价年各指标数据见表3，评价结果见表4。

表3 黑河中游地区评价年指标数据

注：数据来源于甘肃省水资源公报和张掖市统计年鉴。

由表4可知，黑河中游地区2005年水安全评价等级为不安全级别，2011年为临界级别，自2011年以来5年水安全状况从临界级别向安全级别发展。可见，黑河中游地区水安全状况从2005年的不安全级别提升至2011年的临界级别，2011—2015年，研究区水安全状况处于良好稳定态势，水资源生态系统的承载能力逐渐增大，受到外界冲击的损毁程度日益变小。近10年中，张掖市通过水土流失治理、产业结构优化、生态修复建设等系列措施，加大了城市与农村水利建设投入力度，并引入先进的节水灌溉技术，提升了黑河中游地区水安全状态，对该地区未来的规划与发展具有积极意义。

表4 基于指标规范化的正态云模型的水安全评价结果

注：各指标含义见表1。

从表4中水安全评价准则层来看，2005年的生命安全系统处于临界级别，2011—2015年的生命安全系统处于安全级别与临界级别边界；社会经济安全系统在2005年至2011—2015年整体处于安全级别，并逐步向良好级别发展，特别是工业万元产值用水量由2005年的114 m3/万元下降至12.7 m3/万元，反映出地区工业用水水平大幅度提高；生态安全系统处于危险级别和不安全级别，尽管2011—2015年通过治理，状况得到改善，但仍处于不安全级别；生态安全问题是黑河中游地区水安全问题的关键所在；管理安全系统处于不安全至临界级别，2011年至今加大了对水利建设的投资，黑河中游地区水利设施得以修复完善，提高了地区用水水平，管理安全系统的状况有变好的趋势。

从表4中水安全评价指标单个因子的安全状况来看，目前工业用水重复利用率、土壤盐渍化率、森林覆盖率及水利投资占GDP的比例：4个指标处于不安全级别和危险级别。这4个指标对于区域水安全状况具有相当强的制约力或潜在威胁，必须对其进行重点改善。尽管人均水资源量、人均粮食占有量、森林覆盖率等多项评价指标分值都在逐年提升，但该地区土壤盐渍化问题严重，近年来人口增长、城乡发展建设导致水资源供需矛盾的压力也在不断增大，当压力达到临界水平时该地区整体水资源水生态系统的承载能力会迅速下降，抵御外界冲击的能力就会逐步弱化。因此，盐渍化治理和提高工业用水重复利用率、森林覆盖率及水利投资比例等措施是保障黑河中游地区未来水安全的重要前提。

4 结语

在总结国内外相关水安全评价研究与评价模型的基础上，基于指标规范化变换，运用正态云模型对2005年与2011—2015年黑河中游地区水安全状况进行了定量测度，获得以下结论：

1)指标规范化变换使各指标同级标准值差异变小，并且保留了原等级标准值的数字特征，消除了评价指标数量级、量纲与阈值范围方面的各向异性限制，能规范地表达模型评价的不确定性，使得评价结果更科学合理。

2)黑河中游地区的评价结果表明：近10年来，水安全状态从不安全级别上升为临界安全级别并且向安全级别发展，水安全状况日趋变好。但工业用水重复利用率、土壤盐渍化率、森林覆盖率、水利投资占GDP的比例等指标仍处于不安全级别或危险级别，尤其是地下水埋深造成的盐渍化问题，直接影响地区农业生产与生态环境。盐渍化治理和提高工业用水重复利用率、森林覆盖率及水利投资比例等措施是保障黑河中游地区未来水安全的重要前提。

3)目前水安全评价指标标准的确定尚未形成统一标准，水安全问题在不同地域有着不同的特征，如何使水安全评价标准更具通用性和普适性，需要进一步深入研究新型复合评价指标，探索通用性和普适性的评价模型。

[1]陈雷．保护好生命之源,生产之要,生态之基：落实最严格水资源管理制度[J]．求是，2012(14)：38-40．

[2]夏军,朱一中.水资源安全的度量:水资源承载力的研究与挑战[J]．自然资源学报，2002，17(3)：262-269．

[3]张翔,夏军,贾绍峰.干旱区水安全及其风险评价研究[J]．水利学报，2005，36(9)：1138-1142．

[4]LOUCKS D P.Sustainable water resources management[J].Water International,2000,25(1):3-10.

[5]韩宇平,阮本清,解建仓．多层次多目标模糊优选模型在水安全评价中的应用[J]．资源科学，2003，25(4)：37-42．

[6]SULLIVAN C.Calculating a water poverty index[J].World Development,2002,30(7):1195-1210.

[7]曾畅云,李贵宝,傅桦．水环境安全机器指标体系研究:以北京市为例[J]．南水北调与水利科技，2004，2(4)：31-35．

[8]施春红,胡波．城市供水安全综合评价探讨[J]．资源科学，2007，29(3)：80-85．

[9]金菊良,吴开亚,李如忠，等．信息熵与改进模糊层次分析法耦合的区域水安全评价模型[J]．水力发电学报，2007，26(6)：61-66．

[10]吴开亚,金菊良,周玉良，等．流域水资源安全评价的集对分析与可变模糊集耦合模型[J]．四川大学学报(工程科学版)，2008，40(3)：6-12．

[11]李祚泳,张正健,汪嘉杨，等．指标变换值表示的水安全评价的普适指数公式[J]．水利学报，2012，43(9)：1009-1016．

[12]李凤英,王让会,黄俊芳，等．中国西部地区水安全的多指标物元综合评价[J]．干旱区研究，2006，23(2)：269-274．

[13]张龙云,曹升乐,杨尚阳．属性识别理论在水安全评价中的应用研究[J]．山东大学学报(工学版)，2006，36(5)：70-72．

[14]汪嘉杨,王文圣,李祚泳，等．基于TS-SVM模型的水安全评价[J]．水资源保护，2010，26(2)：1-4．

[15]王绍玉,唐桂娟．汶川地震堰塞湖地区水安全综合评价[J]．四川大学学报(工程科学版)，2010，42(增刊1)：76-81．

[16]LI Deyi.Knowledge representation in KDD based on linguistic atoms[J].Journal of Computer Science and Technology,1997,12(6):481-496.

[17]帅青燕,何亚伯．基于云模型的坝基掩体质量综合评价[J]．东南大学学报(自然科学版)，2013，43(1)：54-58．

[18]张杨,严金明,江平，等．基于正态云模型的湖北省土地资源生态安全评价[J]．农业工程学报，2013，29(22)：252-258．

[19]冯学慧．基于熵权法与正态云模型的大坝安全综合评价[J]．水电能源科学，2015，33(11)：57-60．

[20]江辉,张清联,彭建春．基于改进云物元模型的风电场电能质量评价[J]．电网技术，2014，38(1)：3807-3812．

[21]龚艳冰．基于正态云模型和熵权的河西走廊城市化生态风险综合评价[J]．干旱区资源与环境，2012，26(5)：169-174．

[22]李陶,李付伟,李向新，等．地震灾害风险的正态云模型评价:以毕节市为例[J]．中国安全科学学报，2015，25(10)：166-171．

[23]李祚泳,王文圣,汪嘉杨．水资源水环境模型智能优化[M]．北京：科学出版社，2014：194．

[24]周启刚,张晓媛,王兆林.基于正态云模型的三峡库区土地利用生态风险评价[J].农业工程学报,2014,30(23):289-297.

[25]高蔺云,黄晓荣,奚圆圆,等.基于云模型的四川盆地气候变化时空分布特征分析[J].华北水利水电大学学报(自然科学版)》， 2017，38(1)：1-7.

(责任编辑：杜明侠)

Water Security Evaluation Based on Normal Cloud Model with Normalized Indexes

ZHOU Yunzhe, SU Xiaoling

(College of Water Resources and Architectural Engineering, Northwest Agriculture and Forestry University, Yangling 712100, China)

In order to solve the problem that traditional evaluation methods can′t describe the randomness and fuzziness of evaluation indexes at the same time, a normal cloud model was introduced to quantitatively evaluate water security. For overcoming the problem that the evaluation of normal cloud model can′t normatively reflect uncertain problems, the normalization of evaluation indexes were used to unify the value of hyper entropy in normal cloud model, then the evaluation of normal cloud model was normalized. Finally, the region of the middle reaches of Heihe River in Hexi Corridor in Gansu Province was evaluated and investigated using the method. The results indicated: the water security status in the middle reaches of Heihe River was enhanced from insecurity level to a critical level from 2005 to 2011; and it was stable, even had a tendency to become better from 2011 to 2015, but the four indexes of repeated utilization rate of industrial water, soil salinization rate, percentage of forest cover and water conservancy investment proportion in GDP were at dangerous level or insecurity level, the main emphasis of water security construction are taking effective management-control measures at present.

water security evaluation; normal cloud model; the normalization of evaluation indexes; the middle reaches of Heihe River

2016-11-10

“十三五”国家重点研发计划(2016YFC0401306)；国家自然科学基金项目(91425302)。

周云哲(1993—)，男，黑龙江哈尔滨人，硕士研究生，从事水资源合理配置与评价方面的研究。E-mail:zhouyunzhe12345@126.com。

粟晓玲(1968—)，女，四川开江人，教授，博士，从事水资源规划与管理方面的研究。E-mail:suxiaoling17@126.com。

10.3969/j.issn.1002-5634.2017.04.003

TV213.4

A

1002-5634(2017)04-0018-07