待定常数化解分离参数法之困惑
广东省佛山市石门高级中学 (528225) 徐正印
待定常数化解分离参数法之困惑
广东省佛山市石门高级中学 (528225) 徐正印
求参数取值范围的问题常常是高考的压轴题,命题者所提供的解法大都是分类讨论.解决这类问题时,尽管人们首先想到分离参数法,但终因遇到困惑(所涉及的函数的最值用初等数学的方法很难)而放弃!尽管有些专业杂志上已介绍了用洛必达法则去解决,但那毕竟是大学的内容.
本文以近年高考试题为例,阐述如何用待定常数法化解分离参数法之困惑.
例1. (2006年全国高考I卷理科)设函数f(x)=(x+1)ln(x+1),若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.
困惑成因 当x≥0时,f(x)≥ax⇔(x+1)ln(x+1)≥ax⇔当x>0时,(x+1)ln(x+1)≥ax⇔当x>0时,自然想到要求(x>0)的最小值.
破解之道(待定常数法)
为了降低运算量,对分类参数后的式子化为含有待定常数的整式,如:
设g(x)=(x+1)ln(x+1)−mx,(x≥0,m是待定的常数),则 g′(x)=ln(x+1)+1 − m.
待定的常数是这样确定的:使引入函数的导函数值的在定义域内不小于(不大于)零,如:若m=1,则g′(x)=ln(x+1)≥0,在(0,+∞)上,g(x)单调递增,因为所以a≤1.故a的取值范围为(−∞,1].
例2.(2007年高考全国I卷理科)设函数f(x)=ex−e−x.
(I)略;
(II)若对所有x≥0都有f(x)≥ax,求a的取值范围.
分析 当x≥ 0时,f(x)≥ax⇔ee−e−x≥ax⇔当x>0时,
设g(x)=ex−e−x−mx(x≥ 0,m是待定的常数),则 g′(x)=ex+e−x− m.
若 m=2,则 g′(x)=ex+e−x−2,在 (0,+∞)上,g(x)单调递增,g(x)> g(0)=0ex−e−x−2x> 0,ex−e−x> 2x,因为所以a≤2.
例3.(2010年新课标理)设函数f(x)=ex−1−x−ax2.
(I)略;
(II)当x≥0时,f(x)≥0,求a的取值范围.
分析 当x≥0时,f(x)≥0⇔ex−1−x≥ax2⇔当x>0时,ex−1−x≥ax2⇔当x>0时
设g(x)=ex−1−x−mx2(x≥0,m是待定的常数),则g′(x)=ex−1−2mx.
设h(x)=ex−1−2mx(x≥0),则h′(x)=ex−2m.
例4.(2012年高考天津卷理科)已知函数f(x)=x−ln(x+a)的最小值为0,其中a>0.
(I)求a的值;
(II)若对任意的x∈[0,+∞),有f(x)≤kx2成立,求实数k的最小值;
(III)略.
分析 (II)由(I)知a=1,从而f(x)=x−ln(x+1).当x∈[0,+∞)时,f(x)≤ kx2⇔x−ln(x+1)≤kx2⇔当
设g(x)=x−ln(x+1)−mx2(x≥0,m是待定的常数),则
例5.(2014年高考陕西卷理科)设函数f(x)=ln(x+1),g(x)=xf′(x)(x ≥ 0),其中 f′(x)是 f(x)的导函数.
(I)略;
(II)若f(x)≥ag(x)恒成立,求实数a的取值范围;
(III)略.
当x≥0时,f(x)≥ag(x)⇔当x≥0时,ln(x+1)≥⇔当x>0时,ln(x+1)≥⇔当x>0时,
设g(x)=(x+1)ln(x+1)−mx(x≥0,m是待定的常数),则 g′(x)=ln(x+1)+1 − m.
若 m=1,则 g′(x)=ln(x+1)≥ 0,在 (0,+∞)上,g(x)单调递增,g(x)>g(0)=0,(x+1)ln(x+1)−x>0,1.因为所以a≤1.
例6.(2014年新课标II卷理科)已知函数f(x)=ex−e−x−2x.
(I)略;
(II)设g(x)=f(2x)−4bf(x),当x>0时,g(x)> 0,求b的最大值;
(III)略。
分析 (II)因为g(x)=f(2x)−4bf(x),所以当x>0时,g(x)>0⇔当x>0时,f(2x)−4bf(x)>0⇔当x>0时,f(2x)> 4bf(x).因为f(x)=ex−e−x−2x,所以
f(2x)> 4bf(x)⇔ e2x−e−2x−4x≥ 4b(ex−e−x−2x).
设h(x)=ex−e−x−2(x ≥ 0),则 h′(x)=ex+e−x−2≥ 0,在(0,+∞)上,h(x)单调递增,h(x)> h(0)=0,ex−e−x−2x>0.当x>0时,

设

(x≥0,m是待定的常数),则

当m=8时,

g′(x)≥ 0,在(0,+∞)上,g(x)单调递增,g(x)>g(0)=0,
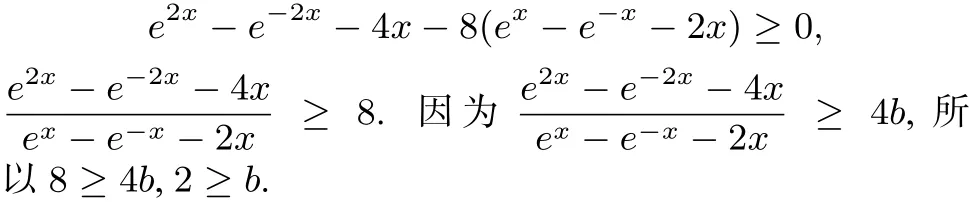
例7. (2015年高考山东卷理科)设函数f(x)=ln(x+1)+a(x2−x),其中a∈R.
(I)略;
(II)若x>0,f(x)≥0成立,求a的取值范围.
分析 (II)当x>0时,
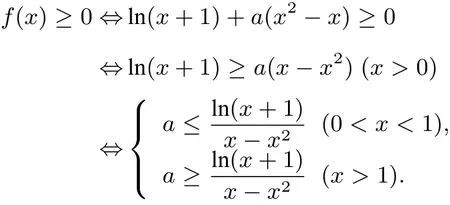
设
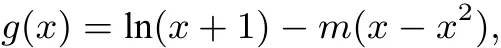
(0<x≤1,m是待定的常数),则
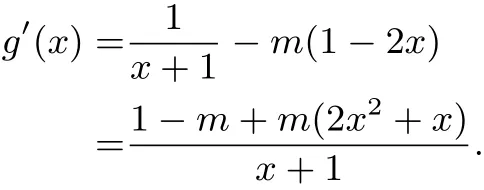

所以a≥0.综上所述,0≤a≤1.
例8.(2016年新课标II卷文科)已知函数f(x)=(x+1)lnx−a(x−1).
(I)略;
(II)若当x∈(1,+∞)时,f(x)>0,求a的取值范围.
分析 (II)当x>0时,f(x)>0⇔(x+1)lnx−a(x−1)>0⇔
设g(x)=(x+1)lnx−2(x−1)(x∈[1,+∞)),则


在(1,+∞)上,h(x)≥ h(1)=0,g′(x)≥ 0,g(x)≥ g(1)=0,即当x∈ (1,+∞)时,(x+1)lnx−2(x−1)> 0,因为对于x∈(1,+∞)恒成立,所以a≤2.则

