变分模态分解和K-L散度在振动筛轴承故障诊断中的应用

徐元博，蔡宗琰

（长安大学 道路施工技术与装备教育部重点实验室，西安 710064）

变分模态分解和K-L散度在振动筛轴承故障诊断中的应用

徐元博，蔡宗琰

（长安大学 道路施工技术与装备教育部重点实验室，西安 710064）

振动筛属于振动机械设备中的筛分设备，其结构特点与运行原理与一般的旋转机械有很大不同，因此提取出的振动信号同从旋转机械提取出的振动信号也同样有较大区别，主要体现在信号中不仅存在大量背景噪声，而且成分也较为复杂。对于此类信号，模态分解算法是个行之有效的方法，模态分解算法在去除大量高频噪声的同时，还能将振动信号分解成一系列具有单一成分的模态分量，从而能更好发现振动信号的物理意义。基于此，引入一种新的故障诊断方法，首先利用变分模态分解将故障信号分解为若干个窄带模态分量，然后根据K-L散度值选定最佳的分量，最后进行包络运算得出故障频率。通过仿真模拟实验与振动筛轴承故障诊断的实际应用，并与之前的经典模态分解算法——经验模态分解和集成经验模态分解进行对比，发现该算法更具有优越性和实用性。

振动与波；振动筛；轴承故障诊断；变分模态分解；经验模态分解；集成经验模态分解

机械设备在正常工作时表现出的振动量在时域和频域都具有一定的数据特征并且具有一定的规律性，一旦检测出实际振动数据的特征量不符合正常工况下的规律性时，即可判定设备的运行有异常情况或存在故障隐患，因此利用振动信号诊断法来判断故障特征已经得到了广泛应用[1]。故障振动信号一般具有较强的非线性与非平稳性特征，同时伴随着噪声与其他振动的干扰，因此为了进行可靠分析，通常要对信号进行有效的前处理。经验模态分解(Empirical Mode Decomposition，EMD)作为一种非线性和非平稳信号的处理方法[2]，得到了很多学者的关注，并把其应用到了故障诊断领域[3–5]，但由于该算法易出现模态混叠现象，其鲁棒性较差。为了克服这一缺陷，N.E Huang等在其基础上提出了集成经验模态分解[6](Ensemble Empirical Mode Decomposition，EEMD)，从而较好地克服了模态混叠现象，因此在故障诊断领域得到广泛关注[7–8]。然而作为噪声辅助型算法，分解后的信号中必然会留下残余白噪声，为了能最大限度消除白噪声，平均集成次数也随之增加，这就造成数据处理时要花费大量时间。基于此，文中采用一种新的自适应信号模态分解方法，即变分模态分解[9](Variational Mode Decomposition，VMD)，相比于EMD和EEMD，该算法具有较好的鲁棒性，而且大大缩短了程序运行时间[10]。文献[11]、[12]和[13]已经将该方法应用到旋转机械的故障诊断当中，但目前VMD算法还未应用于振动机械的故障诊断中，本文将此新方法引入该领域，旨在为振动机械的故障诊断提供一种新的思路与方法。

1 VMD基本原理

VMD的目标就是将一个实数信号f(t)分解为多个互不相关的稀疏性子信号，也就是本征模函数，假设每个模态uk都具有中心频率和有限带宽，约束条件为各模态之和等于输入信号f(t)，且每个模态的估计带宽之和最小，步骤如下[9]。

(1)通过对每个模态函数uk进行希尔伯特变换(Hilbert Transform)得到他们解析信号的单边谱，表达式如下

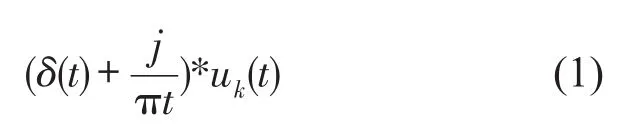
式中δ(t)表示狄利雷克分布函数；*表示卷积。

(2)每个经过Hilbert变换后的模态函数同ejωkt进行混合，使每个模态函数的频谱移频到基带上，表达式如下

式中ωk代表中心频率。

(3)通过梯度的二范数的平方对其模态的带宽进行估计，最终公式如下

式中{uk}={u1，u2，…，uk}代表K个模态函数；ωk={ω1，ω2，…，ωk}代表每个模态函数的中心频率。

为了将约束问题转化为非约束问题，引入二次惩罚因子和拉格朗日乘子，二次惩罚因子用来保证信号重建后的保真度，朗格朗日乘子用来保证其约束的严格性，其扩展的拉格朗日表达式如下

使用Parseval/Plancherel傅里叶等距变换，将式(4)中的uk和ωk的二次优化问题转变到频域,分别得到各模态的频域上的更新，具体表达式如下

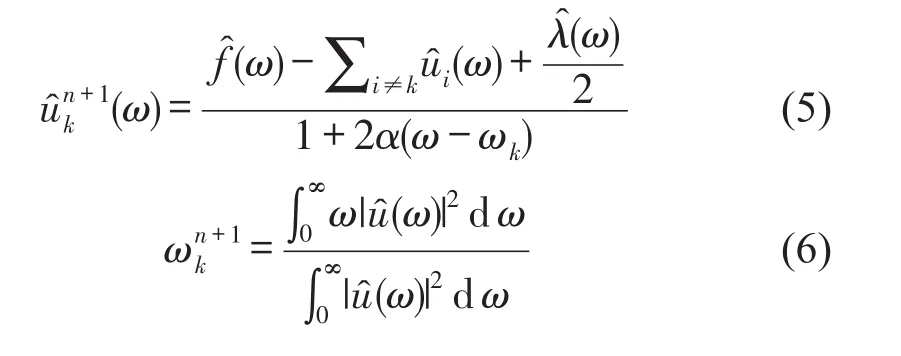
2 K-L散度原理

在概率论和信息论中K-L散度(Kullback-Leibler divergence)也称为相对熵，它是对两个概率分布P和Q之间关系的描述，K-L散度可定义为

上式中P(x)为核密度估计；K(u)为核函数；h为给定的正数，通常称为窗宽或平滑参数。

在真实情况下，信号的分布总是单峰和对称的，因此式(7)变为对称形式下的K-L散度，可定义为

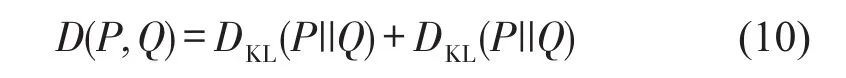
通过上述几式，可最后求得D(P，Q)的散度。

在实际应用当中，P代表实际观察数据的真实分布，而Q代表理论数据的分布，因此可以用P表示实际采集的信号，Qk={Q1，Q2，…，Qk}表示实际采集的信号经VMD分解后的理论子信号，通过比较理论子信号与实际原信号之间的关系远近来选取最佳的子信号进行分析。K-L散度值越小，表明关系越近，是信号的真实成分；反之，则是信号的虚假成分[14]。

3 仿真信号模拟

模拟信号采用文献[9]中的信号，该信号由一个二次函数项、一个Chirp信号和一个分段信号组成，如下式所示，图1为原始信号和各个分量信号波形。

现用EMD、EEMD和VMD对该信号进行分解，如图2所示，三种算法都能将前两个信号分量f1和f2很好的分解出来，但是对于最后一个分量信号f3，EMD的分解是失败的；EEMD有一定的分解作用，但效果仍然很差；而VMD可以很好地将分段信号分解出来，说明VMD在分解性能上有着明显的优势。

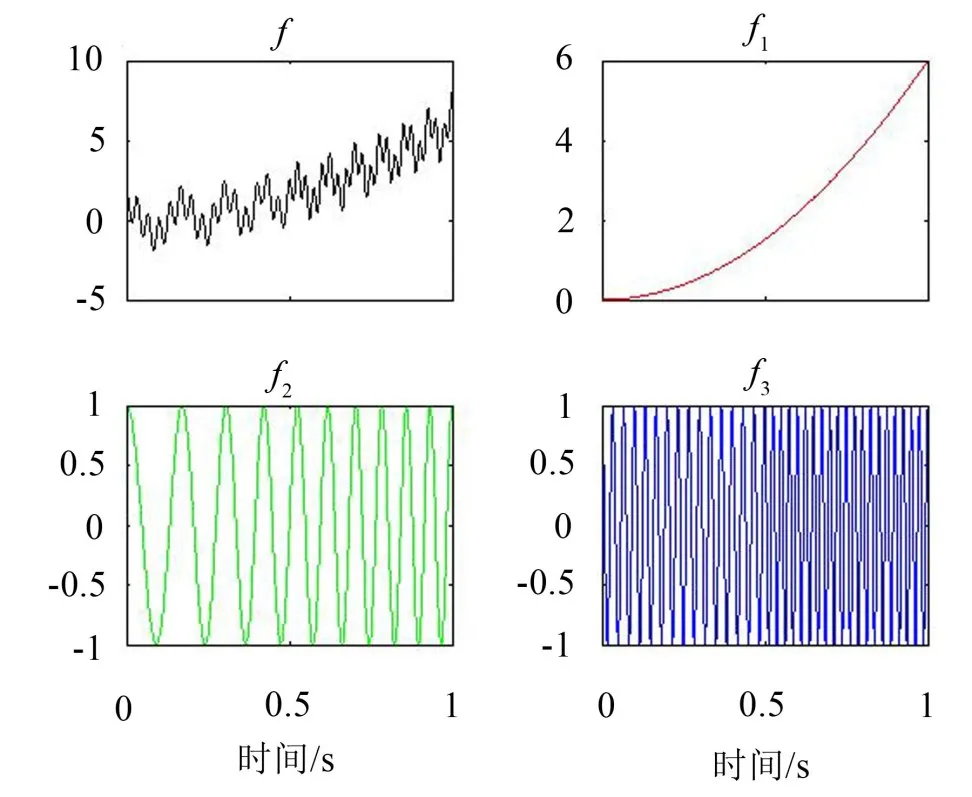
图1 原始信号和分量信号波形

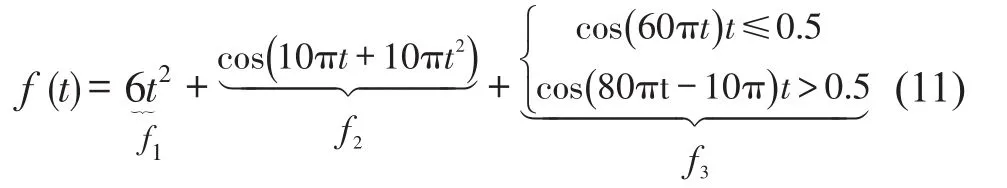
4 振动筛轴承故障应用

4.1 试验目的与安排

实验采用的振动筛如图3所示。分别对滚动轴承进行内环点蚀、外环点蚀，参数如表1所示。轴承内环点蚀故障采样频率为20 kHz，电机轴承的转速为910 r/min，即基频为15.17 Hz，采样点数为10 000，轴承内环的故障频率为fi=146.86 Hz。外环的点蚀故障数据采样频率为100 kHz，采样点数为10 000，轴承外环的故障特征频率为fo=104.92 Hz，理论基频和理论内外环故障频率因误差原因会与真实频率稍有不同。

图2 三种方法分解对比

图3 振动筛

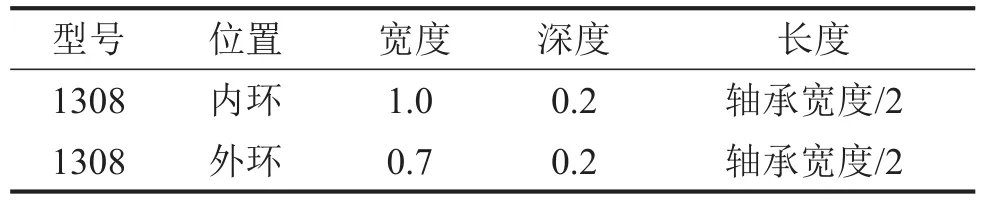
表1 轴承故障参数/mm

为了验证在不同背景噪声下VMD的鲁棒性，实验配备了4块大偏心块和4块小偏心块，同时配以单电机和双电机运转，将它们进行交叉组合来获得不同的振动量级，从而采集不同背景噪声下的数据。

4.2 外环小振动量级实验

外环故障信号如图4所示，从图中可以看出外环故障频率已经被噪声淹没，只有基频频率。

在上一章节仿真信号实验中，可以看出EMD表现最差，因此实验中仅使用EEMD和VMD进行对比，其分解结果如图5所示。

利用K-L散度从中选取与原信号相似度最大的分量，散度值如表2所示。

表2 K-L散度值

从中分别选取值最小的模态分量做包络处理，其包络谱如图6所示，两者都能较好提取出故障频率。

从图7可以看出在背景噪声较小的情况下，两者的差别不是很大，因此这里采用时频图对比，可以看出两者的外环故障频率谱线发生了波动，说明在噪声的干扰下，发生了频率混叠现象，但VMD波动较小，而EEMD的波动较大，说明VMD的抗混叠效应明显强于EEMD，噪声对其影响较小。

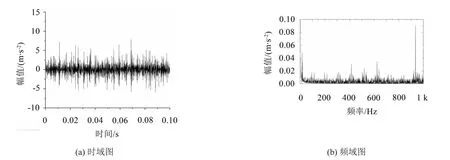
图4 外环原始信号

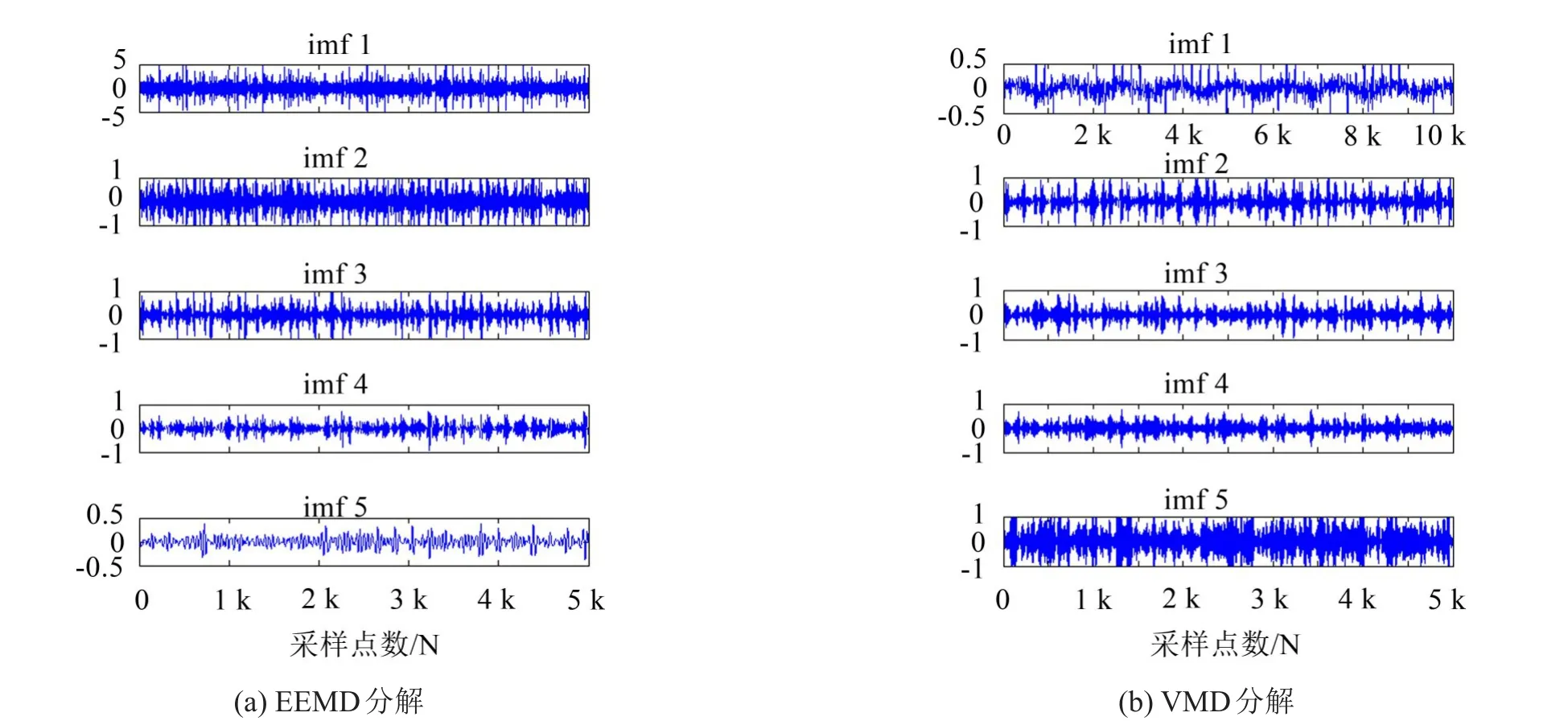
图5 模态分解对比

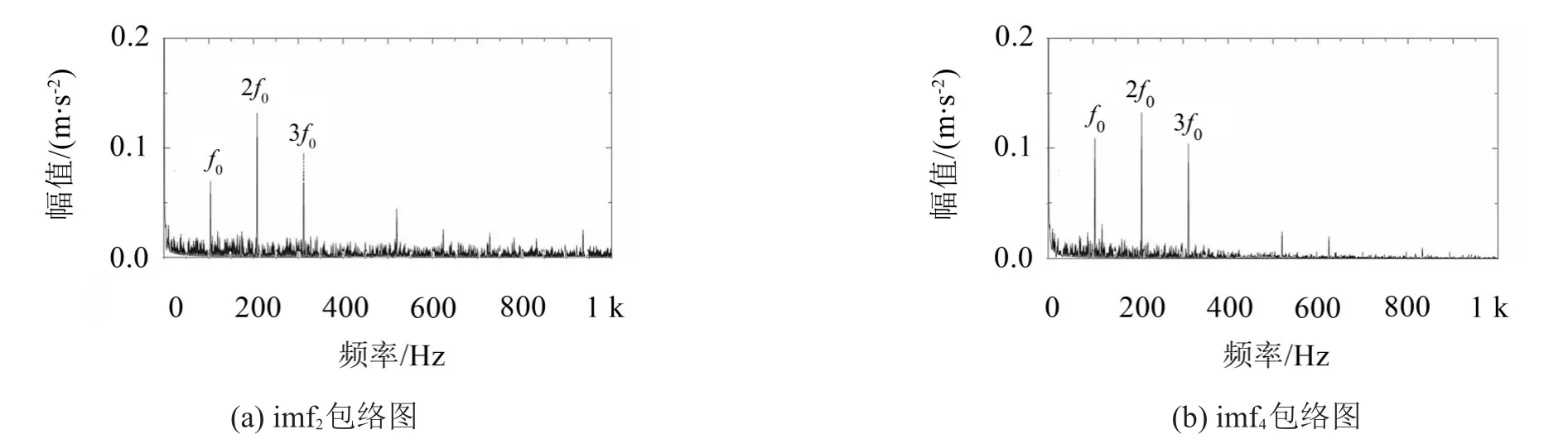
图6 外环故障特征对比

图7 外环故障时频对比

4.3 内环大振动量级实验

内环故障信号如图8所示，内环故障频率已经被噪声淹没，只有基频频率。

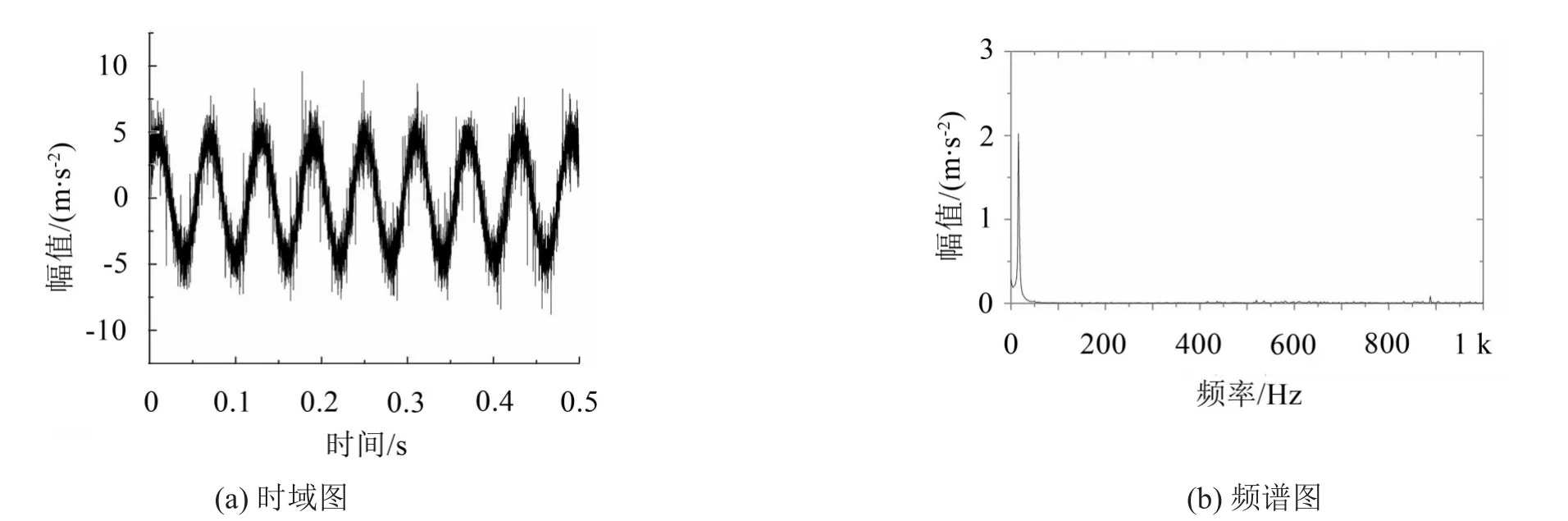
图8 内圈原始信号

图9 模态分解对比

在实验中发现一个值得注意的现象，在大、小振动量级下，波形有着很大的不同。当振动强度大时，波形趋于正弦波，如图8(a)所示；当振动强度小时，波形趋于直线，如图4(a)所示。用EEMD和VMD对信号进行分解，结果如图9所示，分解后的一组分量的波形为正弦波，并且该分量的频率与基频15.17 Hz同频且能量主要集中于基频，具有突出的峰值，如图10所示。通过以上现象，判定大偏心块对传动轴产生较大的受力影响，从而传动轴在旋转时产生了明显的不平衡现象。可以看出，从振动机械中提取的信号相比旋转机械，成分更加复杂。

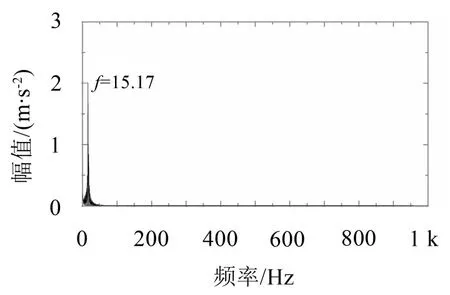
图10 VMD分解imf1分量频谱图

利用K-L散度从中选取与原信号相似度最大的分量做包络处理，散度值如表3所示，其包络谱如图11所示，在背景噪声强烈的工况下，EEMD分解的imf2的包络谱中只显示出故障频率的倍频，而故障频率未明显的显现出来；而VMD分解的imf3的包络谱中故障频率清晰可见。

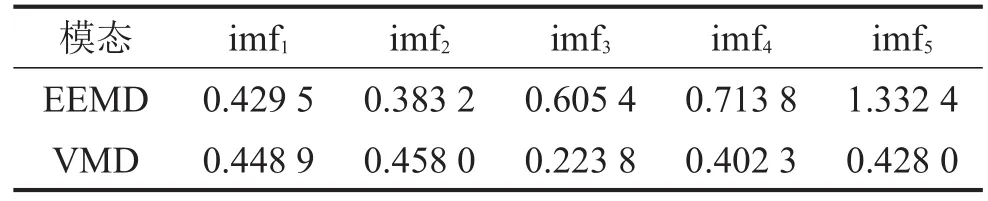
表3 K-L散度值

图12为时频图对比，可以看出随着背景噪声的增大，EEMD分解的内环故障频率谱线相比于外环，波动变得更加剧烈，说明频率混叠更加严重。而VMD分解的故障频率谱线相比于外环，波动无明显差别，如图13所示，说明VMD对噪声敏感性较弱，噪声强度的加大对其影响较小。

5 结语

(1)通过仿真实验和振动筛轴承故障诊断实验发现，相比于EMD和EEMD，VMD对于信号的分解效果更加理想，并且有更好的噪声鲁棒性。

(2)振动机械与旋转机械运行原理不同，因此在运行时，会产生更大背景噪声，而且掺杂的其他频率成分较多，因此在采用振动测量法进行故障诊断时，对算法的鲁棒性要求更高，可以看出VMD在此方面的应用也是有效的。

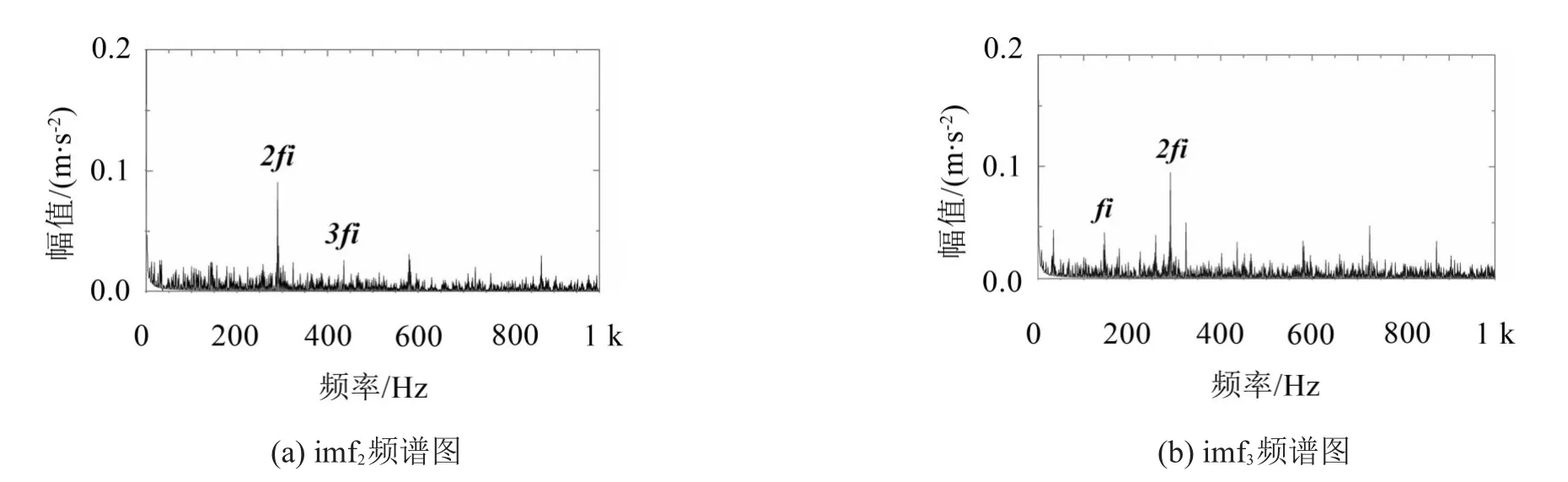
图11 内圈故障特征对比

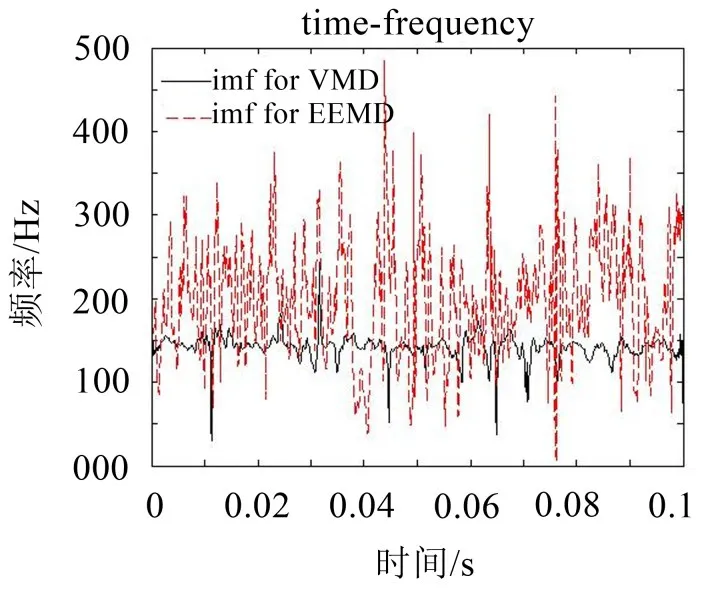
图12 内环故障时频对比

图13 VMD外环与内环故障时频对比

[1]普亚松，郭德伟，张文斌.故障诊断技术在煤矿机械设备中的应用[J].工矿自动化，2015，41(4)：36-39.

[2]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbertspectrum for nonlinearand nonstationary time series analysis[J].Proceedings of the Royal Society of London,1998,454(A):903-995.

[3]吴虎生，吕建新，吴庐山，等.基于EMD和SVM的柴油机气阀机构故障诊断[J].中国机械工程，2010，21(22)：2710-2714.

[4]冷军发，荆双喜，禹建功，等.EMD与能量算子解调在提升机齿轮箱故障诊断中的应用[J].煤炭学报，2013，38(2)：531-535.

[5]石瑞敏，杨兆建.基于改进EMD的多绳摩擦提升机载荷信息特征提取[J].煤炭学报，2014，39(4)：782-788.

[6]WU ZHAOHUA,HUANG NORDEN.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[7]夏均忠，苏涛，张阳，等.基于EEMD能量熵及LS-SVM滚动轴承故障诊断[J].噪声与振动控制，2014，34(3)：170-175.

[8]佟雨燕，陆森林.信号相关性和EEMD-Hilbert包络在滚动轴承故障诊断中的应用[J].噪声与振动控制，2013，33(5)：144-149.

[9]DRAGOMIRETSKIY K,ZOSSO D.Variational mode decomposition[J].IEEETransactionsonSignal Processing,2013,62(3):531-544.

[10]谢平，杨芳梅，李欣欣，等.基于变分模态分解-传递熵的脑肌电信号耦合分析[J].物理学报，2016，65(11)：(118701-1)-(118701-9).

[11]马增强，李亚超，刘政，等.基于变分模态分解和Teager能量算子的滚动轴承故障特征提取[J].振动与冲击，2016，35(13)：134-140.

[12]刘长良，武英杰，甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J].中国电机工程学报，2015，35(13)：3358-3366.

[13]唐贵基，王晓龙.变分模态分解方法及其在滚动轴承早期故障诊断中的应用[J].振动工程学报，2016，29(4)：639-648.

[14]韩中和，李文华.基于K-L散度的EMD虚假分量识别方法[J].中国电机工程学报，2012，32(11)：112-117.

Application of Variational Modal Decomposition and K-L Divergence to Bearing Fault Diagnosis of Vibrating Screens

XU Yuan-bo,CAI Zong-yan
(Key Laboratory of Road Construction Technology and Equipment,Chang’an University,Xi’an 710064,China)

Vibrating screen is a kind of vibrating equipment in the field of vibrating machines,whose characteristics of structure and principle of operation are quite different from those of rotating machinery.Therefore,there is a large difference between the vibration signals extracted from the two different kind of machines.The vibration signals emanating from the vibrating screens contain a great deal of background noise as well as complex components.The mode decomposition algorithm is an effective method for this type of signals.The mode decomposition method can remove the background noise a great deal.Simultaneously,it can decompose the given signal into a series of mono-components to find physical meanings of the vibration signal.On this basis,a new non-recursive Variational Mode Decomposition(VMD)method is presented in this paper.This method can avoid the mode mixing and has a better robustness.This method firstly decomposes a fault signal into several different unknown modes,and then K-L divergence method is employed to select the sensitive modes.Eventually,the fault frequency of the selected modes is detected by envelope demodulation.The results of simulation and bearing fault experiments of the vibrating screen indicate that the proposed method can effectively extract fault features.In comparison with previous mode decomposition methods,such as Empirical Mode Decomposition(EMD)and Ensemble Empirical Mode Decomposition(EEMD),the feasibility and superiority of this method is verified.

vibration and wave;vibrating screen;bearing fault diagnosis;variational mode decomposition;empirical mode decomposition;ensemble empirical mode decomposition

TH133.33；TG806文献表示码：A

：10.3969/j.issn.1006-1355.2017.04.031

1006-1355(2017)04-0160-06

2017-01-12

中央高校教育教学改革专项经费建设项目资助(jgy16049、0012-310600161000)；中央高校基本科研业务费专项资金资助(310825153313)

徐元博（1986－），男，西安市人，博士研究生，主要研究方向为机械振动及故障诊断。

E-mail:2016025001@chd.edu.cn