往复压缩机十字头滑块故障的小波包敏感特征提取研究

李 震，刘 韬，陈 庆

（昆明理工大学 振动与噪声实验室，昆明 650000）

往复压缩机十字头滑块故障的小波包敏感特征提取研究

李 震，刘 韬，陈 庆

（昆明理工大学 振动与噪声实验室，昆明 650000）

由于往复压缩机振动信号具有非平稳和低信噪比特点，利用传统的时域或频域分析方法很难提取到反应压缩机的运行状况有效特征。压缩机发生故障时，信号能量沿频率的分布与正常状态有较大差异，本文利用小波包对非平稳信号的分解和时域重构能力，提出一种基于小波包分析的多频带平均能量特征提取方法；针对各特征对故障的敏感度不同，提出了一种基于欧式距离的特征选择方法，选择的特征能较好地反映压缩机的运行状态，最后通过往复压缩机的实验数据验证了该方法的可行性和有效性。

振动与波；往复压缩机；小波包；平均能量；欧氏距离；特征选择；故障诊断

往复式压缩机质量大，结构复杂，工作过程中气缸内压力易脉动，因此其振动信号具有振源多、信噪比低的特点，采集到的信号不仅具有较强的非线性和非平稳性，同时常伴有周期信号、冲击信号及随机信号等，使得往复压缩机的信号采集、状态监测和故障诊断难度加大。由于往复式压缩机工作原理和自身结构的限制，使得在通用旋转机械上比较成熟的分析方法和诊断技术不能被很好地推广到压缩机的故障诊断中[1–2]。小波包分析对信号具有高分辨率分解和重构能力，能将信号分解到不同频段，进而根据需要灵活选择有效频段进行故障信号重构，分离出故障信息。另外小波包分析具有很高的时频分辨率，使故障的特征提取能在更加细化的频带内进行，进而有效地提取出振动信号中含有冲击成分的故障特征，因此在提取非平稳冲击信号的故障特征中得到广泛应用[3]。唐贵基等将小波包和包络谱分析相结合，成功从轴承振动信号中得到轴承的故障特征频率[4]；张辉等将小波包和自相关算法结合，成功从强背景噪声信号中提取到滚动轴承的故障特征频率[5]；李友荣，曾法力等将小波包分析应用于齿轮箱的故障诊断中，也取得较好效果[6]。往复式压缩机故障诊断的关键在于从原始信号中提取到有效的特征，邹龙庆等人将LMD方法与样本熵相结合，以样本熵作为特征成功诊断出压缩机轴承间隙故障[7]；丛蕊等将EMD方法和关联维数相结合，用各固有模式分量的关联维数作为特征，成功分辨压缩机气阀的不同故障类型[8]。

当往复式压缩机发生故障时，其振动信号的某些频段能量会发生较大变化[9]。文中结合小波包对信号具有高分辨率分解和重构的特点和故障时信号频带能量与正常时的差异性，提出一种基于小波包和频带能量的故障特征提取方法；先利用小波包提取到各频带能量，而后用欧式距离对特征进行选择，找出对故障敏感的特征集，从而实现对往复式压缩机十字头滑块的故障诊断。最后通过实验验证所提方法在压缩机十字头滑块故障诊断中的可行性与有效性。

1 理论基础

1.1 小波包分解[10]

定义函数un(t)的闭包空间是是函数u2n(t)的闭包空间，同时un(t)必须满足下面的双尺度方程

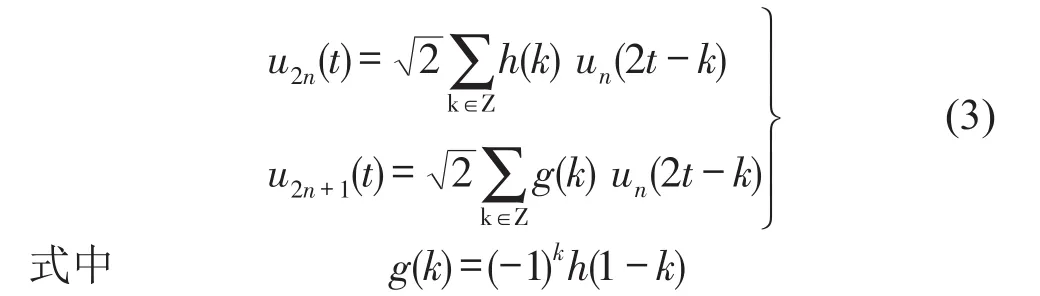
则满足以上条件的序列{un(t)}被称为基函数u0(t)=ϕ(t)的正交小波包。当n取值0时u0(t)和u1(t)分别为尺度函数ϕ(t)和小波基函数Ψ(t)，又根据{un(t)}是正交尺度函数ϕ(t)的正交小波包，可得出也就是{un(t)}能够构成Hilbert空间L2（R）的规范正交基。

小波包各节点时域信号重构算法是

1.2 频带平均能量特征提取

由小波包分解原理和小波包分解树[11]可知，随着分解层数的增加，信号高频成分和低频成分的分解程度，越来越精细。信号经过N层小波包分解后，可以得到信号在某一频段内的特征信息，即原振动信号的能量被分解到2N个正交频带上，各频带上的能量总和与原信号的能量一致，每个频带内的振动信号表征原信号在该频率范围内的振动特征。小波包分解是对信号的正交分解，各分解频带内的信号互相独立，它们无冗余，不疏漏，小波包信号分解遵循能量守衡原理，故有如下关系

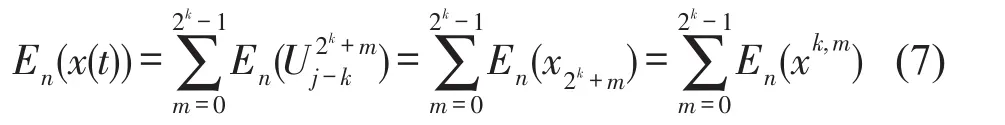
则根据小波包分解原理，信号的总能量Eall等于某一层所有节点信号的能量总和。以分解三层为例，对分解后的8个节点进行重构，得到各节点时间信号为s3,0(t)、s3,1(t)、s3,2(t)、s3,3(t)、s3,4(t)、s3,5(t)每个节点处频带能量的计算方法如下

将式子转化成离散形式是

其中n代表原始信号的长度，xj,k（j=0,1,2,3……7，k=1,2,3……n）表示重构节点s3,0(t)处离散信号的幅值。为了消除数据长度带来的影响，用各频带平均能量代替总能量，即

这几个频带平均能量构成了最初的特征向量T（E3,0，E3,1，E3,2，E3,3，E3,4，E3,5，E3,6，E3,7）。

欧氏距离能很好反应特征对故障的敏感程度，欧氏距离越大，特征对故障越敏感。两个n维向量a(x11，x12，x13，……x1n)与b(x21，x22，x23，……x2n)间的欧氏距离计算公式为

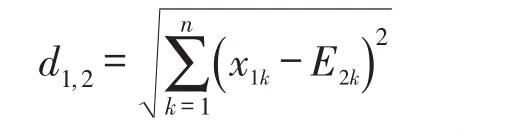
基于小波包分解的频带平均能量特征提取步骤如下：

(1)将振动信号进行N层小波包分解，得到从低频到高频2N个频带；

(2)利用小波包重构各频带时域信号，并求得各频带平均能量T1；

(3)利用欧氏距离对特征T1进行选择得到优化后的特征向量T。；

(4)通过特征向量T实现压缩机十字头滑块的故障诊断。

2 实验验证

十字头是连接压缩机动力部分和执行部分的关键部件，对整个传动链的正常运行起着关键作用；它直接承受来自气缸组件的各种负载力。在交变负载力的作用下，起连接作用的十字头销及铜套很容易受到磨损。经验表明，十字头销和铜套处的故障是十字头故障中最常见的故障之一。采集某石化企业生产现场使用的DW-47/1-2.2型氢气循环压缩机左十字头处的振动信号，电机转速为500 r/min，加速度传感器型号为EK-43790I 9200CSA，灵敏度为100 mv/g，数量为一个，传感器安装如图1所示。

图1 传感器安装位置

采集卡采样频率为25 600 Hz，采样点数为25 600；采样间隔为30 min；每种状态下分别采集6组数据，图2（a）绘制了正常状态下的某一组信号，图2（b）绘制了故障状态下的某一组信号，选用Daubechies II(db2)共轭正交小波基，按照上述方法进行4层小波包分解，并分别求得这两组信号的16个频带平均能量特征如图2（c，d）所示。图中的16个x坐标点从左至右依次对应 E4,00、E4,01、E4,03、E4,02、E4,06、E4,07、E4,05、E4,04、E4,12、E4,13、E4,15、E4,14、E4,10、E4,11、E4,09、E4,08。

根据采样定理，在采样频率为25 600 Hz的情况下，所能分析的频率范围是0～12 800 Hz，由小波包分解重构原理可知，16个平均能量特征对应的频率范围如表1所示。

图2绘制出正常状态和故障状态下的时域波形，从中可以看到即使压缩机正常工作，信号中依然存在明显的冲击成分；发生故障后，冲击成分随之增加，信号幅值增大，信号总能量增加；但除此之外并不能得到更多的故障信息，更无法判断这些能量是哪些频段的信号带来的。加之压缩机信号的强非线性和非平稳性，很难直接用这种原始信号对压缩机进行故障诊断。对6组正常状态信号和6组故障状态信号别进行分析,得到各特征的结果如图3所示。

表1 各个特征对应的频率范围/kHz

图2 正常、故障状态信号及平均能量特征

图3 16个平均能量特征对比图

图4 16个平均能量特征的欧氏距离图

从中可看到当压缩机工作正常时，振动信号的能量主要集中在低频段E4,00和E4,01（0至1 600 Hz）及中 高 频 部 E4,05、E4,04、E4,12、E4,13、E4,15（5 600 Hz 至8 000 Hz）；由压缩机工作原理可知，低频部分的能量一部分是由曲柄滑块机构各部件的惯性力引起，另一部分是由气缸内周期性变化的压力通过活塞和活塞杆传递到十字头上所引起。由于滑块与滑履之间存在着正常的装配间隙，即使润滑条件良好，在滑块运动到远止点和近止点时，由于它的受力方向和运动方向突然变化，所以产生一定的冲击力，这个冲击力是中高频段主要能量的来源；正常情况下这个冲击力较小，因而中高频段能量也较小。图3中分别画出了6组正常数据和6组故障数据的16个特征大小的对比图，表2列出了从正常状态到故障状态16个特征变化的平均值。从中可以清楚地看到，随着压缩机的运转，润滑油的品质下降，曲柄滑块机构各配合部件之间的间隙变大，尤其是滑块和滑履之间间隙增加，使得滑块在远、近止点产生的激振力越来越大。进而激起机器附近更多零部件在其固有频率处的振动，使得这些频率附近的能量显著增加，而这些固有频率主要集中在中高频部分，这也是中高频段能量快速增加的主要原因；但这个冲击力并没有影响到曲柄滑块的惯性力和气缸内的脉动压力；因而低频部分能量基本上保持不变。而在8 000 Hz以上的更高频带部分的能量也基本保持不变，这可能是由于故障处于初期，并没有激起零部件更高的固有频率。从以上分析可以看出，每个特征对故障的敏感度存在较大差异，为了得到更能反应压缩机运行状态的特征集，同时剔除对故障不够敏感的特征，对得到的16个特征分别求其正常状态和故障状态下的欧氏距离，如图3所示，根据结果可认为欧氏距离小于25的特征对故障不敏感，并将其剔除，得到最优的特征集为[E4,05E4,04E4,12E4,13E4,15]。为了进一步检验所选特征集的有效性和优越性，选择压缩机发生故障前两个月的数据，分别绘出所选5个特征的历史趋势图以及低频部特征E4,00和E4,01、高频部分特征E4,11和E4,09的历史趋势图如图5和图6所示。压缩机从正常状态演变到故障状态，特征E4,05、E4,04E4,12、E4,13、E4,15的值变化最为明显，而其他频段能量变化较小，这可能是因为压缩机十字头滑块部分发生故障时所激起的零部件的固有频率主要集中在4 800 Hz至8 800 Hz之间的中高频部分，并不在8 800 Hz以上的高频部分。同时经过选择后的这几个特征能很好反映压缩机整个工作状态的变化。

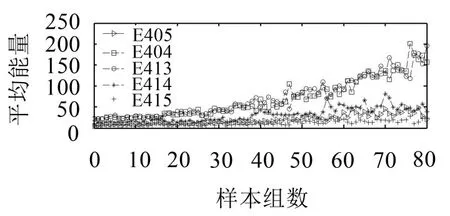
图5 5个敏感特征历史趋势图

图6 不敏感特征（在高低频段分别选择两个）历史趋势图

3 结语

由于往复式压缩机结构复杂并且传感器只能布置在壳体外面，采到的信号是壳体内多种部件振动信息的综合，基于FFT的频谱分析方法很难区分这类机器是否发生故障。而小波分析是傅里叶分析思想方法的发展与延拓。它既继承和发展了短时傅里叶变换的局部化思想，同时又克服了窗口大小不随频率变化的缺点，是处理时往复式压缩机振动信号比较理想的工具。文中利用小波包分解理论在信号特征提取上的优势，以小波包各频带平均能量作为特征参数，并结合欧氏距离对特征进行优化选择，进而得到对故障更为敏感的5个特征，最后绘出这5个特征的历史趋势图，发现能很好地反应出十字头滑块部分的运行状态，进而验证了此方法在压缩机十字头滑块诊断中的可行性和有效性。

表2 正常状态和故障状态下各能量特征平均变化量

[1]TRAN V T,ALTHOBIANI F,BALL A.An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaiser energy operator and deep belief networks[J].Expert Systems with Applications,2014,41(9):4113-4122.

[2]屈梁生，张海军.机械诊断中的几个基本问题[J].中国机械工程，2000，11(z1)：211-216.

[3]何正嘉.机械设备非平稳信号的故障诊断原理及应用[M].北京：高等教育出版社，2001.

[4]唐贵基，蔡伟.应用小波包和包络分析的滚动轴承故障诊断[J].振动、测试与诊断，2009，29(2)：201-204.

[5]张辉，王淑娟，张青森，等.基于小波包变换的滚动轴承故障诊断方法的研究[J].振动与冲击，2004，23(4)：127-130.

[6]李友荣，曾法力，吕勇，等.小波包分析在齿轮故障诊断中的应用[J].振动与冲击，2005，24(5)：101-103.

[7]邹龙庆，陈桂娟，邢俊杰，等.基于LMD样本熵与SVM的往复压缩机故障诊断方法[J].噪声与振动控制，2014，34(6)：174-177.

[8]丛蕊，高学良，刘树林，等.EMD和关联维数在往复压缩机故障诊断中的应用[J].东北石油大学学报，2008，32(2)：86-89.

[9]赵俊龙.往复式压缩机振动信号特征分析及故障诊断方法研究[D].大连：大连理工大学，2010.

[10]彭玉华.小波变换与工程应用[M].北京：科学出版社，1999，70-85.

[11]程正兴，杨守志，冯晓霞.小波分析的理论算法进展和应用［M］.北京：国防工业出版社，2007：120-127.

Sensitive Feature Extraction of Cross-head Slider Faults in Reciprocating Compressors Based on Wavelet Packets

LI Zhen,LIU Tao,CHEN Qing
(The Laboratory of Monitoring and Control of Vibration and Noise,Kunming University of Science and Technology,Kunming 650000,China)

Since the vibration signal of reciprocating compressors is unstable and has low SNR,it is difficult to extract the effective features in operation conditions of the compressors by using the traditional time domain or frequency domain analysis methods only.When the reciprocating compressor is faulted,the distribution of signal energy vs.the frequency is very different from that in the normal operation condition.In this paper,a method to extract the feature of multi-band average energy is proposed based on wavelet packet analysis.Due to the different sensitivity of each feature to the faults,a feature selection method is put forward based on Euclidean distance.The selected feature can effectively reflect the operation state of the compressor.Finally,the feasibility and effectiveness of the proposed method is verified by the test data of the reciprocating compressors.

vibration and wave;reciprocating compressor;wavelet packet;average energy;Euclidean distance;feature selection;fault diagnosis

TH45

：A

：10.3969/j.issn.1006-1355.2017.04.029

1006-1355(2017)04-0150-05

2016-10-11

李震（1990－），男，河南省新乡市人，硕士，主要研究方向为振动与噪声控制。

刘韬，男，硕士生导师。

E-mail:ynliutao@hotmail.com