线加热实现枕型船体外板成形的弹性有限元分析

王江超, 黄文嘉, 常利春, 周 宏， 鞠理杨， 刘建峰

(1. 华中科技大学 船舶与海洋工程学院， 湖北 武汉 430074；2. 江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003；3.上海外高桥造船有限公司， 上海 200137)

线加热实现枕型船体外板成形的弹性有限元分析

王江超1, 黄文嘉1, 常利春1, 周 宏2， 鞠理杨3， 刘建峰3

(1. 华中科技大学 船舶与海洋工程学院， 湖北 武汉 430074；2. 江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003；3.上海外高桥造船有限公司， 上海 200137)

基于固有变形理论和弹性有限元分析，以氧-乙炔火焰加热的固有变形为输入参数，应用弹性有限元分析预测船体板材的面外变形；对比两种不同加热模式下板材受热弯曲成形的效率。研究分析表明，弹性有限元分析可高效地预测板材成形的效果，且从边缘到边缘的平行线加热模式，更有利于板材的弯曲成形。

板材成形；线加热；固有变形；弹性有限元分析

0 引 言

在现代造船中，板材成形是钢材加工处理的重要环节。其中，线加热技术(水火弯板工艺)被广泛地应用于船体曲面外板的生产和加工中[1]。早期，通过线加热技术实现板材成形主要依赖于经验丰富的技术工人，然而这需要工人通过长期的工作实践积累经验并熟练掌握其中的规律和加工工艺。基于技术工人的线加热工艺，所需要的生产成本过高，且生产效率不足，尤其是针对特殊或复杂弯曲成形要求的船体外板，无法保证其产品质量。

随着高性能电子计算机和数值分析技术的快速发展，计算机辅助板材成形得到了越来越多的推广和应用[2]。热弹塑性有限元分析可以很好地再现线加热板材成形过程中的各种物理现象：热传导导致的不均匀温度场分布；弹塑性应变的产生以及面外的弯曲变形情况。然而，上述方法的计算速度取决于研究对象有限元网格的疏密程度以及加载的时间步长和收敛准则的设定。因此，在实际的生产实践中，热弹塑性有限元分析具有相当大的局限性。板材弯曲成形中所需要的面外变形来源于线加热过程中产生的塑性应变(固有应变)，本文以固有变形为计算分析的输入参数，仅通过快速的弹性分析来预测线加热产生的弯曲变形，计算过程高效且结果精度有保证，可满足实际生产的需求。

1 研究理论和方法

本文主要通过加载固有变形的弹性有限元分析，预测线加热过程产生的弯曲变形。相关的研究理论和方法如下。

1.1 固有应变

基于大量的试验观察以及热弹塑性有限元计算的结果分析，焊接过程中剩余压缩塑性应变是产生焊接变形的根本原因[3]。焊接加热冷却过程中的全应变εtotal可以分为如式(1)所示的几个分量：弹性应变εelastic、热应变εthermal、塑性应变εplastic、蠕变应变εcreep和相变产生的应变εphase。总应变可以考虑为弹性应变与固有应变之和。换言之，固有应变εinherent是除弹性应变之外的其他应变分量的总和，即固有应变是热应变εthermal、塑性应变εplastic、蠕变应变εcreep和相变产生的应变εphase的总和，如式(2)所示。固有应变可以简单地使用塑性应变来表示，因为焊接过程中蠕变应变和材料固态相变引起的应变一般较小，可忽略不计，而热应变会随着焊接结构温度降低至初始温度或室温而消失。因此，塑性应变是组成固有应变的各个应变中最主要的分量形式，并且可以通过试验测量或者热弹塑性有限元分析得到。

(1)

(2)

1.2 固有变形

由于上述的固有应变受到加热温度和母材约束的影响，其在距离焊缝不同远近的位置时有着大小不同的数值。因此，直接加载固有应变进行弹性有限元分析来预测大型复杂船体结构的焊接变形，在实际应用中仍存在一定的局限性。若将垂直于焊缝的横断面上的所有固有应变分量进行积分求和，则可得到对应分量的固有变形，如图1和式(3)所示。并且，对于足够长的焊缝，在忽略焊缝端部效应后，每个焊缝的力学特征可由4个固有变形分量来表达[4]：

(3)

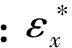
图1 典型对接焊缝中的固有变形分量

1.3 弹性有限元分析

应用上述固有应变和固有变形的概念和理论，弹性有限元分析可以实施。具体的过程可分为以下几步来进行。

(1) 有限元建模。首先针对研究的板材，在商业有限元软件Patran中建立对应尺寸的几何模型，并应用Shell单元进行网格划分。由于弹性有限元分析加载的是固有变形，因此可以使用较大尺寸的单元，在提高计算效率的同时，并不影响最终的计算结果。

(2) 弹性求解。使用日本大阪大学开发的程序(JWRIAN)进行固有变形的加载和弹性求解。其中，在线加热路径两侧的Shell单元上施加对应的固有变形分量(面内收缩和面外弯曲力矩)。分析的板材物理性能参数以及计算的边界条件也需要在相关的输入文件中进行设置。

(3) 后处理分析。Weld-STA是由上海交通大学船舶海洋与建筑工程学院的船舶力学工艺研究所开发的数值分析平台，其拥有较为强大的后处理功能，包括：应力、应变以及各方向变形云图；某条线上各点的各方向变形分布；某个点各方向变形在整个计算过程中的变化情况。

2 固有变形数值估算

在应用弹性有限元分析进行板材成形研究之前，需要得到线加热产生的固有变形，且固有变形数值的精度直接影响甚至决定最终预测的板材弯曲尺寸。本文研究的线加热技术使用的火焰加热工艺参数如表1所示。图2为固有变形分量与热输入(线能量)之间的关系。

表1 线加热技术中火焰加热工艺参数

由于燃料(氧-乙炔)的燃值为12 800 cal/L，则得到该线加热产生的线能量为

(4)

因此，产生的纵向收缩和横向收缩可通过如下公式获得

(5)

(6)

角变形(横向弯曲力矩)可从图2b)中获得(0.006 r/min)，而纵向弯曲因其数值过小，在计算中往往不予考虑。

图2 固有变形分量与热输入(线能量)之间的关系

3 枕型板材加工过程中的弹性有限元分析

如已知线加热所产生的固有变形(面内收缩和面外弯曲力矩)，则可将其作为输入参数，在Shell单元建立的板材模型中进行弹性有限元分析，可快速得到可靠的数值分析结果。通过对具体板材尺寸、线加热工艺以及最终的板材形状进行研究，则可应用弹性有限元计算，实现对加工过程的数值模拟。

3.1 板材的有限元模型

本次研究分析的对象是厚度为30 mm，长和宽都为500 mm的正方形钢板(弹性模量为210 GPa，泊松比为0.3)。在Patran软件中建立相对应的有限元模型，且在计算分析时，固定6个节点的自由度(Degree of Freedom， DOF)作为边界条件。

常见的船体外板成形有3种结构形式：枕型、马鞍型和扭转型。本文主要针对上述(500 mm×500 mm)的正方形板材，通过表1的火焰加热参数来实现枕型的线加热板材成形，并基于弹性有限元分析进一步研究加热路径对实际船体板材成形的影响。

3.2 从边缘至边缘的线加热

根据具体的线加热模式，在Patran软件中建立有限元模型，其网格划分情况如图3所示。该模型包含11 025个节点和10 000个Shell单元。图3所示的有限元网格模型中，不同颜色的区域之间将施加一条或者多条线加热。

图3 正方形钢板的有限元模型及网格划分(Case 1)

图4给出了从边缘到边缘的线加热(Case 1)路径，首先1～4号水平线加热同时施加，然后在竖直方向同时施加5～8号的线加热。一次完整的线加热过程，可完成总计8条加热路径，其总长为4 000 mm，得到的面外变形分布及其数值如图5所示。

图4 线加热路径(Case 1)

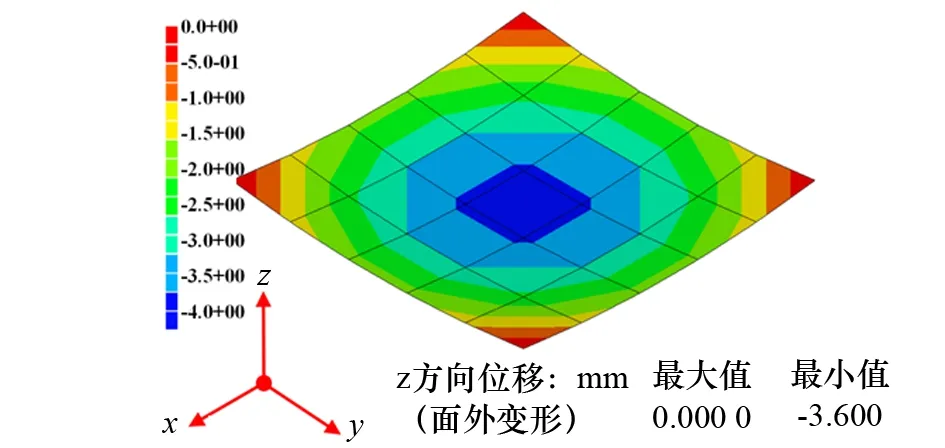
图5 一次完整的线加热产生的面外变形(Case 1)

3.3 从边缘至中心的线加热

按照上述方法，建立从边缘至中心进行线加热的有限元模型，其网格划分情况如图6所示。该模型包含10 489个节点和9 984个Shell单元。同样地，图6所示的有限元网格模型中，不同颜色的区域之间(除去中心区域)将施加一条或者多条线加热。图7给出了线加热的路径，1～8号线加热同时从边缘向中心区域施加，其总长约为1 738 mm，最终得到的面外变形分布及其数值如图8所示。

图6 正方形钢板的有限元模型及网格划分(Case 2)

图7 线加热路径(Case 2)

3.4 结果讨论

针对上述两种不同的线加热模式(Case 1：从边缘至边缘的线加热；Case 2：从边缘至中心的线加热)，通过有限元建模以及热弹塑性分析，可对其生产效率和制造精度进行对比，具体如表2所示。在

[][]

相同线能量的条件下，从边缘到边缘的平行线加热，具有更高的板材弯曲效率。其在船体外板成形中，得到了广泛应用。

表2 不同线加热模式的参数对比

4 结 论

本文使用弹性有限元方法，分析使用线加热进行30 mm船体外板成形的制造过程，不仅介绍了弹性有限元分析的相关理论和方法，同时应用该方法还研究使用两种不同线加热模式进行枕型板材结构成形的过程。相关的结论总结如下：

(1) 将焊接固有变形理论引入到线加热的板材成形预测中，并在固有变形的基础上，介绍弹性分析的各个步骤及具体内容。

(2) 针对具体的线加热工艺参数，估算出对应的固有变形数值。

(3) 初步应用弹性有限元方法，预测给定线加热工艺条件下可能产生的面外弯曲变形数值。

(4) 针对船体弯板的枕型结构，考虑并分析两种不同线加热模式下得到的面外弯曲变形，通过对比，评估两种线加热模态的优劣。

以后，还将在复杂线加热轨迹的智能化网格划分、高效且精确的加热方法应用以及建立真实外板形状与线加热轨迹、热源强度之间关系等方面进行详细且深入的研究。

[1] 徐兆康，胡毛宇.船舶建造工艺学[M].北京：人民交通出版社，2000.

[2] UEDA Y, MURAKAWA H, RASHWAN A M, et al. Development of computer aided process planning system for plate bending by line-heating(report 1)：relation between the final form of plate and the inherent strain (machanics, strength & structural design)[J]. Transactions of Jwri, 1991,20:275 -285.

[3] 上田幸雄, 村川英一, 麻宁绪. 焊接变形和残余应力的数值计算方法与程序[M].罗宇, 王江超,译.成都：四川大学出版社, 2008.

[4] ADAN V S. Development of inherent deformation database for automatic forming of thick steel plates by line-heating considering complex heating patterns[D]. Osakai: Osaka University, 2009.

Elastic FE Analysis on Plate Forming of Pillow Shape by Line Heating

WANG Jiangchao1, HUANG Wenjia1, CHANG Lichun1, ZHOU Hong2， JU Liyang3， LIU Jianfeng3

(1.School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074，Hubei， China;2.School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology, Zhenjiang 212003, Jiangsu, China;3.Shanghai Waigaoqiao Shipbuilding Co., Ltd., Shanghai 200137, China)

The intrinsic deformation of oxygen acetylene flame heating is taken as input parameter based on the theory of internal deformation and elastic finite element analysis. The efficiency of ship plate bending under two different heating models is compared, it can be drawn that elastic finite element analysis can be used to predict ship plate bending effectively and it is better for plate bending with parallel heating pattern.

plate forming; line heating; inherent deformation; elastic FE analysis

中央高校基本科研业务费专项资金资助(2015MS102)；高技术船舶科研专项子专题(15921019518)；江苏高校高技术船舶协同创新中心(HZ2016009)

王江超(1983-)，男，副教授，博士生导师,主要研究方向为计算焊接力学在船舶建造中的应用，船舶海洋结构物集成化建造及结构力学性能评估

1000-3878(2017)04-0014-04

U671

A