浅谈小学数学教学中几何直观能力的培养

赵惠卿

摘 要：几何直观所指有两点：一是几何，在这里几何是指图形；二是直观，这里的直观不仅仅是指直接看到的东西（直接看到的是一个层次），更重要的是依托现在看到的东西、以前看到的东西进行思考、想象，综合起来，几何直观就是依托、利用图形进行数学的思考和想象。它在本质上是一种通过图形所展开的想象能力。

關键词：小学生；数学；几何直观能力

作为一线教师，我们应全面理解几何教育价值，重视对学生几何直观能力的培养。那么，在教学中如何培养学生的几何直观能力呢？

一、在日常学习中逐步培养学生画图的习惯

在日常教学中，帮助学生养成画图的习惯是非常重要的。可以通过多种途径和方式使学生真正体会到画图堆理解概念、寻求解题思路带来的益处。动手画图要从小开始培养，比如一年级上册练习有这样的一道题：小红的前面有3个人，后面有4个人，小红他们这一组一共有多少人？学生看到这个题目后，列出的算式是：3+4=7（人）。教师在讲评中列出算式3+1+4=8（人），强调为什么要加1，因为小红在这个队伍中也算一个。学生“哦”一声，只知道小红也是一个，要加1，而过段时间后，碰到类似的题目，学生又全部忘了。如果在分析这道题时，我们能借此向学生渗透线段图，如：

这样讲解以后，学生在遇到类似的题目就会想到用画图解决，慢慢就养成了画图的习惯了，解题的准确率也提高了。

二、重视变换，让图形动起来

几何变换或图形的运动是几何，也是整个数学中很重要的内容，它既是学习的对象，也是认识数学的思想和方法。变换又可以看作运动，让图形动起来是指在认识这些图形时，在头脑中让图形动起来。比如《圆的周长计算公式》，在测量圆的周长时，教师可以鼓励学生用不同的方式进行测量，如用一块圆形木板（或硬纸板），用线（或纸条）绕圆一周，量得它的长度。也可以在圆上画一个点，在直尺上滚动一周直接量出圆的周长。学生用测量的方法量出了这些圆的周长以后，教师可以进一步提出问题：“要是有一个很大的圆，怎么测量它的周长呢？比如圆形花坛。”也许学生会说可以拿测量土地的卷尺绕花坛一周进行测量，教师可以举出更多的圆的例子，引导学生去寻求更为一般化的方法。在这儿，教材为学生直接指明了研究的方向，即通过测量不同大小的圆的周长和直径，计算出周长和直径的比值，使学生发现，不管圆的大小怎么变化，圆的周长总是直径的三倍多一点。根据圆的周长和直径的倍数关系，可以得出求圆的周长的计算公式。这样充分利用变换去认识、理解圆的周长，学生在运用时就会想起公式的由来，对公式的理解就更深刻了。

三、学会画平面图分析和解决问题

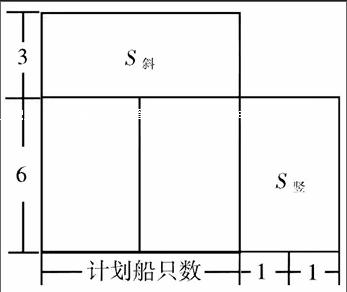
我们学过画线段图来分析应用题，这样做可以使问题具体、形象。但是，在我们解答一些要同时考虑两个因素的应用题时，如果用长方形的长和宽分别表示两个不同的因素，画出长方形来，再利用长方形的面积进行分析，往往更方便一些。长方形图解应用题主要是“抓住面积不变，借助一个量增加，则另一个量减少”这一基本规则来解决问题。比如，有一个班的学生去划船，若增加一只船，则每只船刚好坐6人；若减少一只船，则每只船刚好坐9人，该班共有多少人？此题以前我们都是用假设法来解这种题，今天我们试着用长方形图解（如图）

用长方形的长表示船只数，用宽表示每船坐的人数。由题意，S斜=S竖，S竖=6×2

6×2÷3=4（只）…（计划船只数少一只）

9×4=36（人）…总人数

还可以这样想：S白=2S竖（空白长方形的宽是斜条长方形宽的2倍；长相同），把空白长方形分割成两个面积相等的长方形，S斜=S竖，总人数可用3S竖来表示：6×2×3=36（人）…总人数。

运用“长方形图解法”进行教学，来解答类似的应用题，不仅可使题目化难为易，而且能提高学生的解题能力，促进学生思维的发展，有效发展学生的几何直观能力。

综上所述，我们在整个数学教学中重视几何直观能力的培养，就能让几何直观在教学中发挥着把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。希望数学教师重视它，在日常教学中帮助学生不断提升这种能力，让几何直观在学习数学中发挥它应有的重要作用。

参考文献：

希尔伯特.直观几何[M].王联芳，译.高等教育出版社，1959.

编辑 鲁翠红endprint