引力波及激光观测原理

韩 潇 刘宇星

(北京工业大学应用数理学院,北京 100124)

引力波及激光观测原理

韩 潇 刘宇星

(北京工业大学应用数理学院,北京 100124)

近期引力波话题火热，为使本科生对引力波有系统的了解，本文由爱因斯坦经典引力理论出发，考虑在远离场源的弱场近似，细致推导得到波速为光速、在空间上以横波形式传播的引力波的波动方程，并且指出引力波只存在两种独立的极化状态，即引力波两个独立的偏振方向。之后对激光观测引力波实验的理论进行合理性分析。得出装有法布里-珀罗腔结构的迈克耳孙干涉仪具备观测引力波能力的结论。

引力波； 爱因斯坦引力场方程； 弱场近似； 激光观测

1 引力波概述

1916年，当广义相对论(GR)的场方程完成后，爱因斯坦预言存在一种引力波。他发现广义相对论线性弱场方程具有波动方程形式的解:由场源质量四极矩的时间变化产生的空间应变横波，其传播速度为光速，通俗地讲，就是一种由质量引起的弯曲褶皱在时空上传播形成的波[1]。作为一个物理理论，广义相对论除了预言水星轨道的近日点进动、光子轨线的引力偏折、光频率的引力红移3大经典检验以外，还在20世纪成功预言引力透镜效应[2]以及银河系中心人马座黑洞[3]等。广义相对论还剩下的一个重大预言引力波在最近有了新进展。

自2016年2月11日L I GO宣布发现引力波[4]，社会各界兴起引力波讨论热，近期再次观测到引力波[5]，更是将讨论热度提到最高，与此同时人们不禁产生了一些问题：引力场具有何种的数学描述？引力理论究竟如何在弱场条件下得到波动形式解？引力波的形式是什么样的？光束的传播依托时空，若时空发生褶皱那又如何由光束体现时空褶皱？等等一系列问题引起本科生的困惑。虽然这些内容在大部分教科书(如朗道《场论》等)均有涉及，但对于大部分理工科未选修广义相对论课程的学生，这些问题是无法被理解的。本文由最基础的引力理论开始，逐步介绍引力波的波动方程及物理意义；同时对于少部分选修过广义相对论课程的学生，会发现本文比教科书更为详细地讨论了弱场条件下波动方程的得出，并且较详细地讨论了两种极化的物理意义。

2 弱场方程

对于爱因斯坦场方程

(1)

(2)

可见雷曼张量与时空度规因子gμ ν是场方程的重要组成，因此讨论空间曲率张量特性即可预见场方程的某些属性。

爱因斯坦提出广义相对论时就已经预见引力波的振幅非常小，对此，考虑距离波源极远的情景笔者将引力波看作平直空间中有极化方向的线性波，假设爱因斯坦场可以分为背景场和引力波两项，并且认为背景场是慢变的，引力波是快变的。因此对于时空曲率可以写出[7]

(3)

式(3)右边两项分别对应背景场和波动项。应注意的是，此式中4个指标都在下面，这并不是严格意义上的雷曼张量，但由度规因子很容易得到：

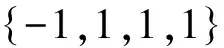
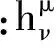
这种度规的扰动没有对参考系作唯一确定的选择，即x′i=xi+ξi处扰动度规仍保持为小量。

3 波动方程与极化场

雷曼张量由度规的二阶协变微商*协变微商Aα,β在有些教科书又写作∂βAα，再例如hαα,ν,ν又写作∂ν∂νhαα的线性组合确定[9]，这是由于

(4)

(5)

代入则有

(6)

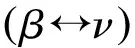
(7)

将β与ν交换展开，则有

(8)

用未扰动的度规ηα ρ对度规小量升降运算，特别注意到，式中第四项在升指标后为对hμν的全微分：

(9)

相似的，对于Ricci标量

(10)

同时考虑到上一节中提到对于hμ ν为小量应在任意参考系变化下成立，即对于坐标变换x′i=xi+ξi，有：

(11)

(12)

将Rμ ν与R代入式(1)，并由上式条件化简，则对于Ricci张量和度规扰动hμ ν可以得到简单的场方程如下[10]

(13)

考虑引力场在远离引力源的真空中传播，则能动张量Tμ ν=0

(14)

这是一个三维波动方程，对比电磁波的波动方程：

(15)

发现形式极为相近，hμ ν可视为引力波场。

利用转置无迹规范(transverse traceless gauge)，即假设引力波沿z轴传播，震动方向垂直于z轴，引力波张量与时间t有关的都为零，且引力波场无迹。则hμ ν应只有4个分量

(16)

同时考虑到雷曼张量的对称性(对于Rαβμν有34指标反称，12指标反称，34、12指标对称，234指标循环反称)，以及场无迹这一基本假设，分别得到hyx=hxy；hxx=-hyy。因此hμ ν只有两种独立的极化状态，即h+和h×。任何引力场的极化都是由这两种极化的线性组合得到。

对于转置无迹规范的引力波，注意到雷曼张量是度规的二阶协变微商的线性组合，可以回到雷曼张量，因此将波动方程改写成下式：

(17)

指标0表示沿t轴的矢量；雷曼张量是含时的，且沿z轴以光速传播，因此必然可以写为Rμ 0ν 0=Rμ 0ν 0(t-z/c)的形式。同时类比度规hμ ν分量的简化，同样有Rx 0x 0=-Ry 0y 0，Rx 0y 0=Ry 0x 0。对此方程求解，有：

(18)

h+和h×为极化正弦波，A+和A×为极化振幅。

4 动力学方程

考虑两个在弱场中的小质量检验对象A和B处在垂直于引力波传播方向的平面(x-y面)，当引力波经过它(由无到有)，根据牛顿引力理论，引力势函数与源的关系由泊松方程决定，

(19)

(20)

(21)

两检验粒子的相对加速度为

(22)

左式：

右式：

因此有潮汐力方程[11]

(23)

对于广义相对论的引力势场，可以写作雷曼张量表述形式，

(24)

并将式(12)代入替换有

(25)

对于两检验对象的情况，考虑其一在(0,0,z)，另一在(x,y,z)位置，则有

(26)

(27)

积分则有

(28)

(29)

对于上式的物理解释：当一个检测质量环在引力场中，且垂直于引力波的传播方向并假设z轴坐标为零，则质量环的运动规律如图1。

图1 引力波经过两个偏振方向时引起的时空变化

具体分析：以圆心为坐标原点，x轴上两点Px1(-x0,0)，Px2(x0,0)，y轴上两点Py1(0,-y0)，Py2(0,y0)。当引力波相位在-π/2到π/2之间时，Px1在x方向的偏离Δx<0，而关于原点对称的Px2则有Δx>0，这是由于Δx=hxxx0，式中x0在Px1、Px2两点分别为-x0、x0。因此在此阶段质量环的横向间距变大。由于引力波振幅hxx=-hyy，因此纵向间距与横向间距相反，在相位在-π/2到π/2之间时，纵向间距变小，且与横向的变化量相同，类似的，同样分析π/2到3π/2的情况，则刚好相反。

对于另一单一极化状态，经过相似的步骤运

算推导，也有类似的结果：质量环在某一方向上伸缩震荡。

5 激光观测

根据定义两个自由悬浮做测地运动的检验质量之间相对加速度(加速度梯度)可以表示为下式[12]

(30)

其中ξα为相对位移，uν为检测质量四速度，λ为仿射参数。

同时观察(26)、(27)两式，当引力波作用两检验质量时产生加速度，即检验粒子具有能量，此能量会使粒子在引力波经过之后继续作简谐运动。可见当引力波经过时，光束可以测量空间中两检验粒子的距离变化。因此引力波的探测是可行的。

图2 单偏振引力波在时空中传播*Made by Mathematica 10.2

(31)

关于迈克耳孙干涉仪的著名实验迈克尔逊-莫雷实验证实以太不存在，为狭义相对论的出现作铺垫。如今LIGO等引力波观测实验也采用此原理，或许将证实广义相对论的一大预言。

如图为激光观测迈克耳孙干涉仪的原理图，对于波长λ，两光束相位差为[13]

(32)

(33)

显然此观测方法观测频率是有范围的，干涉仪臂长L越大响应越强。如LISA的敏感频段在3mHz[14,15]，考虑4亿光年外两个重达10万倍太阳质量的黑洞相互绕转，释放的引力波振幅在传播到地球时强度是10-21量级，对应相距5×106km的检验质量相对位移为10pm[13]。对于频率为100Hz，对应臂长应为75km，这对于地面实验显然是无法做到的。因此，各实验组均对迈克耳孙干涉仪进行改进，加入法布里-珀罗腔结构，使得激光在腔中多次循环，以减小腔长。

图3 迈克耳孙干涉仪原理图

6 结语

综上，基于光速不变时空间隔为零这一特点的激光观测引力波在理论上是合理的((31)(33)式)，对于引力波振幅极小这一困难，在技术上通过多次反射折叠使用法布里-珀罗腔结构控制输出相位，做到放大作用。这同样也是合理的，因此LIGO对于两黑洞绕转系统的引力波观测是较为可信的。

[1]EinsteinA.Hamilton’sprincipleandthegeneraltheoryofrelativity[J].Sitzungsber.Preuss.akad.wiss.berlin, 1916.

[2]LewisA,ChallinorA.WeakgravitationallensingoftheCMB[J].PhysicsReports, 2006, 429(1): 1-65.

[3]FarrellSA,WebbNA,BarretD,etal.Anintermediate-massblackholeofover500solarmassesinthegalaxyESO243-49.[J].Nature, 2009, 460(7251): 73-5.

[4]AbbottBP,AbbottR,AbbottTD,etal.ObservationofgravitationalwavesfromaBinaryblackholemerger[J].PhysicalReviewLetters, 2016, 116(6).

[5]Abbott,B.P.,etal.GW151226:Observationofgravitationalwavesfroma22-Solar-MassBinaryblackholecoalescence[J].PhysicalReviewLetters, 2016, 116(24).

[6] 黄玉梅,王运永,汤克云,等.引力波理论和实验的新进展[J].天文学进展,2007,25(1):58-73.HuangYumei,WangYunyong,TangKeyun.Newprogressofgravitationalwavetheoryandexperiment[J].ProgressinAstronomy, 2007, 25(1): 58-73. (inChinese)

[7] 刘雪敏. 测量引力波的新方法光孤子存储环-共振棒测引力波[D].华中科技大学,2004.LiuXuemin.Anewmethodformeasuringgravitationalwave.Anopticalsolitonstoragering-resonantrodforgravitationalwavemeasurement[D].HUST. 2004. (inChinese)

[8] 朗道.场论[M].北京：高等教育出版社,1959, 105.

[9] 梁灿彬. 微分几何入门与广义相对论(上)[M].北京：北京师范大学出版社,2000:78-90.

[10] 朗道.场论[M]. 北京：高等教育出版社,1959, 107.

[11] 梁灿彬，周彬.微分几何入门与广义相对论(中)[M].2版.北京：科学出版社,2009.

[12] 王运永, 朱兴江, 刘见,等.激光干涉仪引力波探测器[J].天文学进展,2014(3):348-382.WangYunyong,ZhuXingjiang,LiuJian.Laserinterferometergravitationalwavedetector[J].ProgressinAstronomy, 2014(3): 348-382. (inChinese)

[13]AnzaS,ArmanoM,BalaguerE,etal.TheLTPexperimentontheLISAPathfindermission[J].Classical&QuantumGravity, 2005, 22(10):S125-S138.

[14]ArmanoM,BenedettiM,BogenstahlJ,etal.LISAPathfinder:TheexperimentandtheroutetoLISA[J].Classical&QuantumGravity, 2009, 26(9): 1159-1165.

■

GRAVITATIONAL WAVES AND THE PRINCIPLE OF LASER OBSERVATION

Han Xiao Liu Yuxing

(Applied School of Mathematic Physics Science, Beijing University of Technology, Beijing 100124)

Gravitational waves become a hot issue recently. In order to make the undergraduates have systematic understanding of it, we review the derivation of gravitational waves in this paper. With Einstein classical gravitational theory, we obtain the wave equation from the weak-field approximation, and then we achieve the conclusion that the transverse waves of spatial strain travels at the speed of light. We point out that the gravitational waves exist only two independent polarized states, which means that the gravitational waves have two independent polarization directions. Furthermore, rationality about laser observation of the gravitational waves is analyzed both from theoretical and experimental aspects. Finally, we find a strategy to observe the gravitational waves by using the Michelson Interferometer with Fabry-Perot Cavity.

gravitational waves; Einstein field equations; weak-field approximation; laser observation

2016-06-22

韩潇,男,在读本科生，hx.shadow@qq.com。

韩潇,刘宇星. 引力波及激光观测原理[J]. 物理与工程，2017，27(4)：70-74.