转动弹簧的微变形分析及其应用
陈奎孚
(中国农业大学理学院,北京 100083)

转动弹簧的微变形分析及其应用
陈奎孚
(中国农业大学理学院,北京 100083)
教材中经典的弹簧振子的弹簧不会转动,但工程上弹簧轴线会转动的情形比比皆是。弹簧轴线转动会造成几何非线性,但是围绕平衡位置的微幅振动仍是振动学习的最重要任务。本文先用解析法导出了弹簧微变形的近似表达式,再利用直观的几何关系验证这一表达式,而后者易于理解和记忆。利用3个例题对表达式的威力进行了验证。
振动;微变形;微幅振动;线性振动;几何法;解析法
图1(a)所示的模型是物理教材和振动教材使用频率最高的振动系统[1,2]。该系统在振动过程中,弹簧轴线无转动,因而弹簧变形与系统的描述坐标之间的关系就很简单。然而稍微复杂一点的工程问题中,弹簧轴线就可能有转动,比如图1(b)和图1(c)所示情形,因此工程专业的学生不能止步于教材中的经典例题。此外,一些有趣的特殊振动系统也要考虑弹簧轴线转动[3-5]。
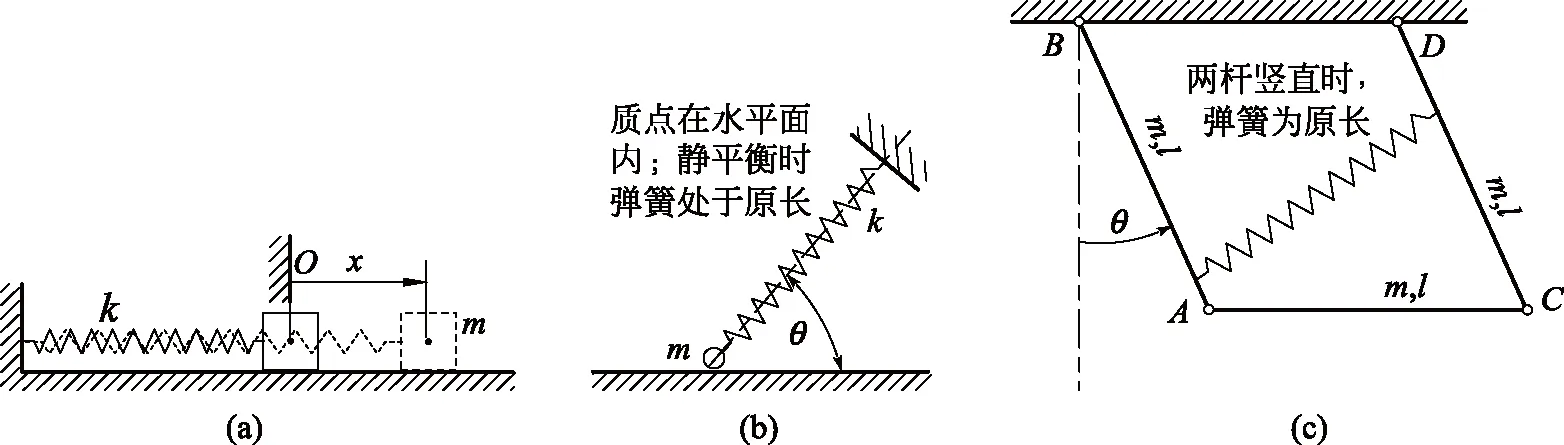
图1 振动系统示例
无论采用分离体的方法,还是采用能量法,振动分析都需要确定弹簧的变形量。但对于弹簧轴有转动的情形,变形量确定因几何复杂性而对学生有挑战性。本来这是技术问题,但是若该技术掌握不好,不仅导致分析速度的下降,更因分析的困难和近似因素取舍的纠结会使学生有挫折感,从而影响学生学习热情和信心。
弹簧轴有转动的情形一般是非线性的,但振动分析起码要得到工程最关心的固有频率, 此时就要研究振动系统围绕平衡位置的微幅振动,这就退化为线性振动。此外,研究微幅线性振动也是进一步深入分析不可或缺的一环。

图2 弹簧在振动中的改变
本文将针对微幅振动的特殊性,利用解析法和几何法两种方法导出弹簧微变形的近似表达式。该近似表达式可以消除学生在分析同类问题时的挫折感。最后通过3个例子演示近似表达式的威力。
1 解析法
假定弹簧不抵抗弯曲,因而弹簧总是直的。在振动过程中,弹簧的改变可分解为如下3种基本模式的组合(见图2(a)):旋转(AB→CD)、平移和伸缩。3种模式中只有伸缩会改变弹性势能。我们来分析弹簧的伸缩量。
为了便于分析,把弹簧端点A和C重合起来,这样就可以构成一个△ABD,如图2(b)所示。图中β是AB和BD之间的夹角;γ是AB和AD之间的夹角。
由正弦定理有
(1)
即
(2)
因此弹簧伸长量为
(3)
在微幅振动过程中,β和γ发生偏离平衡参数的微变化,即β=β0+Δβ,γ=γ0+Δγ,其中:Δβ和Δγ均为微幅量;β0和γ0为平衡位置所对应的参数。作为近似分析,将式(3)微分近似有
即
(4)
注意系统在静平衡位置,AB和CD是重合的,即γ0=0,故式(4)可进一步简化为
(5)
上式表明:δ近似式很简洁,且与Δβ无关。
β0是在静平衡位置下的参数,但是如果只考虑静平衡一个位置,则BD=0,这使得β0不确定。但若从β=β0+Δβ角度考虑,则β0是β当Δβ→0的极限。当Δβ→0,对单自由度系统必有B→D,这样割线BD的方向就趋近于B的轨迹切线方向。因此β0为AB与B点轨迹切向之间的夹角。当然,如果弹簧两个端点都有运动(如图1(c)中弹簧), 则为相对于A的轨迹(图1(c)中B相对于A)。
2 几何法
上述推导过程几何意义不明显,难于记忆。下面介绍有几何意义的近似分析方法。图3中,弹簧用抽象的杆表示。在AD上找到E点,使得AE=AB,这样就有δ=ED。
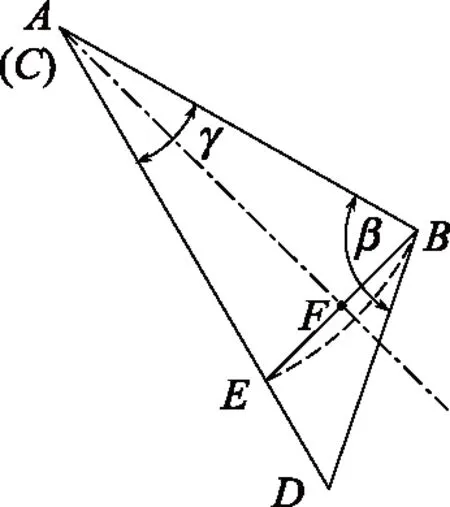
图3 几何法
在△EBD中:∠D=π-β-γ;∠EBD=β-(π/2-γ/2)。由正弦定理有
即得
即
(6)
在微幅情形下,cos(β+γ/2)与cosβ0相差一个小量,而sin(β+γ)与sinβ0相差一个小量,因此式(6)可变为
(7)
如果注意到了BE=2lsin(γ/2)与lγ相差一个高阶小量,那么式(7)就是式(5)。
很多时候BD的信息容易获得,那么对△EBD再度使用正弦定理有
即有
再次使用γ和Δβ为小量的假设有
(8)
式(7)和式(8)的推导过程仍然难于记忆。下面给出较为容易记忆的方法。作∠A的角平分线交于图3中的BE于F。因AB=AE而有AF垂直于BE。当γ→0时,AB和AE趋于平行于AF,因而△BED趋近于∠BED为直角的三角形。
在近似直角△BED中,自然有
它们分别就是式(7)和式(8)。
注意: 上述易记的几何法关键点是:以弹簧原长为腰作等腰三角形;此三角形的高和两腰在微幅振动下都近似垂直于底边;等腰三角形底边、伸缩量和弹簧端点位移近似组成直角三角形(弹簧端点位移为斜边)。
3 应用
例题1 如图4(a)所示,轮子可绕水平轴转动,对轮心的转动惯量为J。轮缘绕有软绳,下端挂有质量m,绳与轮缘之间无滑动。在图示位置,由水平弹簧维持平衡。半径R与a已知。求微幅振动的固有频率p。
解 圆盘转过θ的分析示意见图4(b)。按照通常近似处理,重力只影响平衡位置,所以忽略重力的影响。系统的动能为
在图4(b)的AD上找到E点使得AE=AB。在近似直角△DEB中,DB为斜边。对微幅振动DB≈aθ,因而弹簧伸长量
δ=ED≈DBsin∠EBD≈-a θcosβ0
式中的静平衡位置参数β0见图4(c),易知它为180°,故δ≈aθ。这样弹簧势能
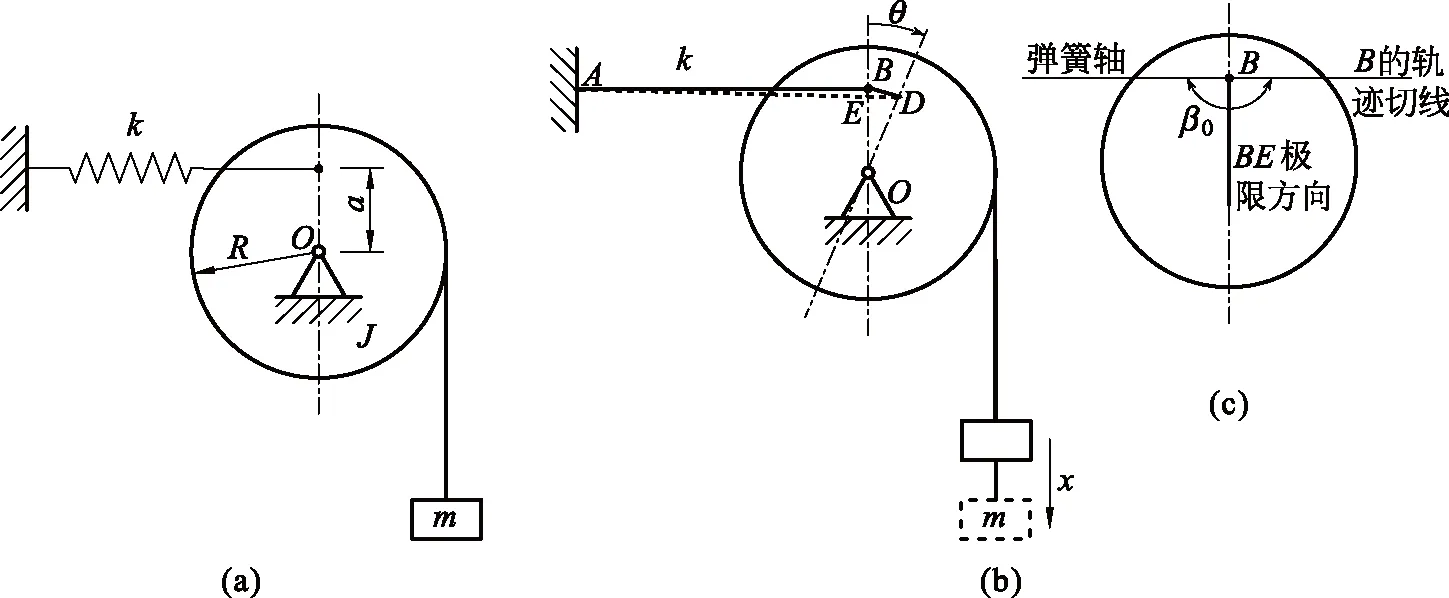
图4 例题1图
得到
例题2 图5(a)中的均质刚性杆,长l,质量为m,杆处于铅垂位置为系统静平衡位置,此时弹簧为原长。求系统固有频率p。

图5 例题2图
解AB发生θ角位移的分析见图5(b)。系统动能为
势能包括弹性势能和重力势能。选择杆竖直为重力势能和弹性势能的零势能点。重力势能
(9)
为求右边弹簧的势能,从FD′的延长线找到E点使得FE=FD。在近似直角△DD′E中斜边DD′≈θl/2是已知信息,因此弹簧缩短量
这样右边弹簧的势能
得到
例题3 图6(a)所示系统中,均质圆柱体质量为m, 半径为R, 只滚不滑,图示为静平衡位置,弹簧处于自然长度。求其固有频率p。
解 此题解答可参考文献[6]。我们这里选择圆柱体的柱心C的位移x为系统广义坐标。系统动能为
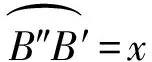

图6 例题3图
在△BB′B″中,EB′≈BB′sin∠B′BE=BB′cos∠B′BH≈2xcos(θ/2)cosβ0。这里β0是静平衡位置时的弹簧轴与B轨迹切线的夹角。由图6(c)可知β0=θ/2。因此右边弹簧缩短量为
这样得到右边弹簧的势能为
类似地可以得到左边弹簧的势能
由瑞利法可以得到固有频率
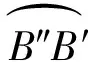
(10)
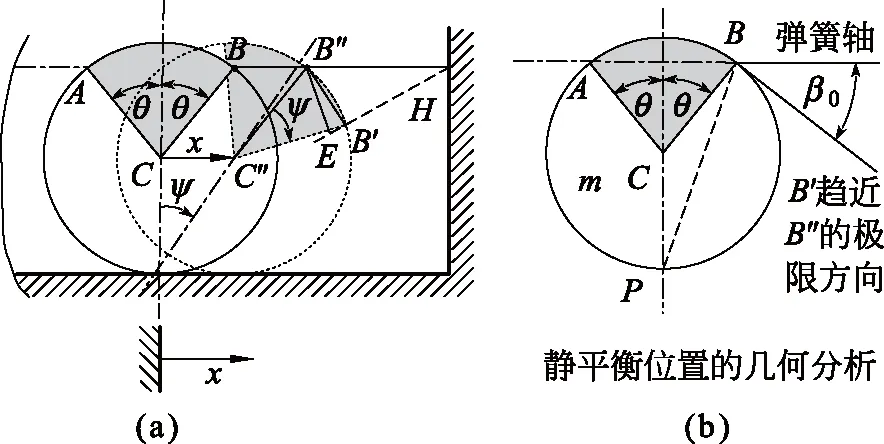
图7 另一种方式确定例题3右边弹簧压缩量
其中β0是B′趋近于B″的极限方向(因为扣除了圆柱的平移分量,所以不再是B的绝对轨迹方向)与弹簧轴之间夹角。由图7(b)的几何关系得到β0=θ。因此右边弹簧缩短量为
4 结语
工程上往往要分析弹簧轴有转动的情形。本文针对最关心的微幅振动的特殊性,推导了弹簧伸缩量的近似表达式。该表达式可大大降低相关问题的分析难度,提高学生学习的信心。
本文建议了一种易记几何法,其关键点是:找弹簧原长的等腰三角形;此三角形的高和两腰对微幅振动情形都是近似垂直于底边的;等腰三角形底边、伸缩量和弹簧端点位移线段近似组成为直角三角形(弹簧端点位移线段为斜边)。
[1] 王少杰,顾牡, 毛骏健. 大学物理学(下册)[M].2版. 上海: 同济大学出版社,2002:97-98.
[2] 陈奎孚. 机械振动教程[M]. 北京:中国农业大学出版社,2014:6-9.
[3] 郭敏,闫诚实,王靖淇,等. 弹簧参与的微小振动一定是简谐运动吗?[J]. 物理与工程,2015,25(3):41-43. Guo Min, Yan Chengshi, Wang Jingqi, et al. Is the micro vibration of spring a simple harmonic motion[J]. Physics and Engineering, 2015, 25(3): 41-43. (in Chinese)
[4] 陈奎孚,蔡春. 仅据平衡位置为系统弹性势能零点就能使振子势能为kx2/2吗?[J]. 物理与工程, 2015,25(2):52-54. Chen Kuifu, Cai Chun. Can the concise form ofkx2/2 for the system potential enegy be taken for granted if merely the equilibrium position is chosen as the zero point of system potential energy?[J]. Physics and Engineering, 2015,25(2): 52-54. (in Chinese)
[5] 陈奎孚,蔡春.关于“对物理教材中两个概念的讨论”中“加减平衡力系”的商榷[J]. 物理与工程, 2015,25(1):59-60. Chen Kuifu, Cai Chun. Remarks on“discussion of two concepts in physics textbooks”[J]. Physics and Engineering, 2015, 25(1): 59-60. (in Chinese)
[6] 邢誉峰.工程振动基础——知识要点及习题解答[M]. 北京:北京航空航天大学出版社,2004.
■
THE MICRO-DEFORMATION ANALYSIS OF AN AXIS ROTATING SPRING AND ITS APPLICATION
Chen Kuifu
(College of Science, China Agricultural University, Beijing 100083)
The canonical vibrators in textbooks do not possess axis rotating springs; however this case is ubiquitous in engineering. The Spring axis rotation causes the geometrical nonlinearity, but it is an essential task to analyze the linear vibration in a micro-scale around its statically balanced configuration. However, this task is a daunting challenge to students because of the sophisticated geometrical relationship. The analytical approach was utilized to derive the approximate spring’s micro-deformation expressions, and then this expression was corroborated by a geometrical approach. The latter is easy to be assimilated and remembered. The power of the approximate expression was demonstrated by three examples.
Vibration; micro-deformation; micro-vibration; linear vibration; geometrical approach; analytical approach
2016-04-26
陈奎孚,男,教授,从事力学和振动的教学研究,chenkuifu@cau.edu.cn。
陈奎孚. 转动弹簧的微变形分析及其应用[J]. 物理与工程,2017,27(4):10-14.
——《势能》

