在加强改进演化方程方法下的(1+1)-维组合KdV-mKdV方程的精确解

刘名权

(朝阳师范高等专科学校，辽宁朝阳122000)

【基础理论研究】

在加强改进演化方程方法下的(1+1)-维组合KdV-mKdV方程的精确解

刘名权

(朝阳师范高等专科学校，辽宁朝阳122000)

为了求解更高维数的发展方程，使用加强改进演化方程的方法来构造非线性发展方程的变系数精确解，并使用这种方法获得了(1+1)-维组合KdV-mKdV方程的精确解，并且从精确解中得到了类孤波解与孤波解．结果表明，在数学物理领域中，使用加强改进演化方程的方法是求解非线性发展方程精确解的有力工具．

加强改进演化方程的方法；非线性发展方程；精确解；类孤波解；孤波解

0 引言

非线性发展方程的精确解在众多物理现象中扮演着重要角色，例如流体力学、光学、离子物理等．近些年来，许多有效的求解方法都已经被用来获得非线性发展方程的精确解，例如：Hirota双线性法[1]、扩展的Riccati方程法[2]、单一代数法[3]、改进G′/G法[4]、指数函数法[5]、齐次平衡法[6]、Darboux变换法[7、8]、Painleve检验法[9]和加强改进演化方程法[10～12]等．这些方法已经得到了许多(1+1)-维非线性发展方程的精确解，当这些精确解[10～12]存在时，满足如下形式

(1)

其中，Ak是常系数，Ψ(ζ)是未知待定函数．

然而，对于(1+1)-维非线性常系数方程很难找到变系数精确解，本文利用加强改进演化方程的方法得到一个常系数非线性微分方程的变系数精确解，且解的形式如下：

(2)

其中Ak(t)是t的函数，Ak(t)与Ψ(ζ)是未知待定函数，且AN(t)≠0．

受文献10～12的启发，作为这种方法的应用本文将对(1+1)-维非线性发展方程求变系数精确解．

1 加强改进演化方程法

假设有如下形式的非线性发展方程

F(u,ut,ux,uxx,…)=0

(3)

其中F是关于u及u的偏导数的多项式，且包含它的最高阶导数和非线性项．下面给出该方法的主要步骤：

步骤1 利用广义变换

u(x,t)=u(ζ)，ζ=p(t)x+q(t)

(4)

其中，p(t)和q(t)是关于t的可微函数，由(3)、(4)我们有如下常微分方程

(5)

其中·≡d/dt,′≡d/dζ．

步骤2 我们假设方程(5)有如下形式的解

(6)

其中Ak(t)是t的函数，Ak(t)与Ψ(ζ)是未知待定函数，且Ak(t)≠0．

步骤3 在方程(5)中使用齐次平衡法来确定方程(6)中的正整数N．

步骤4 我们将(6)式带到(5)式中，通过计算得到未知函数u(ζ)的各阶导数以及函数Ψ(ζ)，通过这种带入我们可以得到关于Ψ-n，Ψ-nx，Ψ-nx2，…，n=0,1,2，…的多项式，并令该多项式的所有系数为0，通过该方法得到的方程组可以确定Ak(t)和Ψ(ζ)，最后我们可以得到方程(3)的精确解．

2 主要结果

在这部分中，我们使用加强改进演化方程的方法来找到以下非线性发展方程的精确解、类孤波解和孤波解．

(1+1)-维组合KdV-mKdV方程

ut+(α+βu)uux+γuxxx=0

(7)

其中α、β、γ是非零常数，并且βγ<0．

方程(7)已经利用改进映射法[13]，Jacobi-elliptic函数法[14～16]讨论过，下面我们将使用加强改进演化方程的方法来研究方程(7)．

首先我们使用广义变换(4)将方程(7)化简为如下常微分方程

(8)

关于ζ对方程(8)进行积分，并让所有积分常数为0，进而得到如下常微分方程

(9)

平衡u3和un项可以得到N=1，因此方程(9)有如下形式解

(10)

其中A0(t)和A(t)是关于t的函数，由此可知A1(t)≠0，我们很容易得到:

(11)

(12)

将(10)～(12)式代入(9)式中，并且让Ψ0、Ψ0x、Ψ-1、Ψ-1x、Ψ-2和Ψ-3项的系数为0，相应得到

(13)

(14)

(15)

(16)

3p(t)A1(t)[αA1(t)Ψ′2+2βA0(t)A1(t)Ψ′2-6γp2(t)Ψ′Ψ″]=0

(17)

(18)

由方程(13)、(14)、(16)、(18)得

(19)

(20)

其中，k为可积常数，且βγ<0．

接下来我们讨论如下两种情形：

情形一.如果A0(t)=0．

在这种情况下，方程(15)和(17)可以化简为

(21)

αΑ1Ψ′-6γk2Ψ″=0

(22)

方程(22)可以得到

(23)

由方程(21)、(23)有

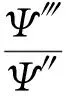
(24)

将方程(24)对ζ积分可有

(25)

最后可得到

(26)

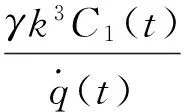
(27)

其中，C1(t)、C2(t)和q(t)是t的任意函数，那么方程(7)有如下形式的精确解

(28)

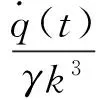
(29)

(30)

若在方程(29)和(30)中，令q(t)=at+b,那么可以得到如下形式的行波解：

(31)

(32)

其中a、b是常系数．

在这种情形下，方程(15)和(17)可以简化为：

(33)

αA1Ψ′+2βA0(t)A1Ψ′-6λk2Ψ″=0

(34)

由方程(34)给出：

(35)

其中G1(t)=A1[α+2βA0(t)]．

将(35)式代入(33)式中，可以得到

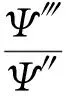
(36)

其中H1(t)=A0(t)[3α+4βA0(t)]．

将方程(36)关于ζ积分有

(37)

由(35)和(37)有

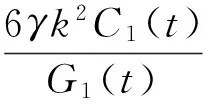
(38)

然后有

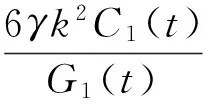
(39)

其中，C1(t)、C2(t)和q(t)是t的任意函数，那么方程(7)有如下形式的精确解

(40)

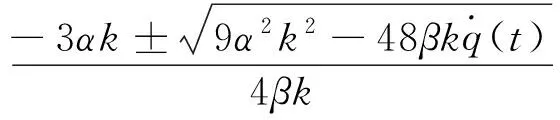
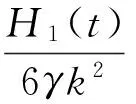
(41)

(42)

若在方程(41)和(42)中，令q(t)=at+b，那么可以得到如下形式的孤波解：

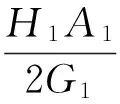
(43)

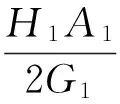
(44)

其中，a、b是任意常系数且

H1(t)=A0[3α+4βΑ0]=H1,

G1(t)=A1[α+2βA0]=G1．

3 结论

本文利用了加强改进演化方程的方法找到了(1+1)-维组合KdV-mKdV方程的变系数精确解，并且从精确解中得到了该方程的类孤波解和孤波解．可以看出,加强改进演化方程的方法直接有效，并且可以应用到一些其他的非线性发展方程中．

[1]R Hirota. Exact Solution of the Korteweg-de Vries Equation for Multiple Collisions of Solitons[J]. Phys. Rev. Lett，1971，27(18)：1192-1194.

[2]Hongqing Zhang. New exact solutions for the Konopelchenko-Dubrovsky equation using an extended Riccati equation rational expansion method and symbolic computation[J]. Appl. Math. Comput，2007，187(2)：1373-1388.

[3]Engui Fan. Multiple travelling wave solutions of nonlinear evolution equations using a unified algebraic method[J]. J Phys A，2002，35(32)：6853-6872.

[5]Jihuan He, Xuhong Wu. Exp-function method for nonlinear wave equations[J].Chaos Solitons and Fractals，2006，30(3)：700-708.

[6]Mingling Wang, Yubin Zhou, Zhibin Li. Applications of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J]. Phys. Lett，1996，A 216(1)：67-75.

[7]Yishen Li, Wenxiu Ma, Jin E. Zhang. Darboux transformations of classical Boussinesq system and its new solutions[J].Phys Lett，2000, A 275(2)：60-66.

[8]D Levi, O Ragnisco. Dressing method vs. classical darboux transformation[J].IL Nuovo Ciento，1984，83(1)：34-42.

[9]John Weiss. The Painleve property for partial differential equations II:Backlund transformation, Lax pairs,and the Schwarzian derivative[J]. J. Math. Phys，1983，24(6)：1405-1413.

[10]A J M Jawad, M D Petkovic，A Biswas. Modified simple equationmethod for nonlinear evolution equations[J]. Appl. Math. Comput，2010，217(2)：869-877.

[11]E M E Zayed. A note on the modified simple equation method applied to Sharma-Tasso-Olver equation[J].Appl. Math. Comput，2011，218(7)：3962-3964.

[12]E M E Zayed,S A Hoda Ibrahim.Exact Solution of nonlinear evolution equations in mathematical physics using the modified simple equation method[J].Chinese Phys. Lett，2012，29(6)：060201-060204.

[13]Zaiyun Zhang, Zhenhai Liu, Xiujin Miao,etal. New exact solutions to the perturbed Schr dingers equation with Kerr law nonliearity[J]. Appl. Math. Comput，2010，216(10)：3064-3072.

[14]Dazhao Lu. Jacobi elliptic function solutions for two variant Boussinesq equations[J]. Chaos Solitons and Fractals，2005，24(5)：1373-1385.

[15]Shikuo Liu, Zuntao Fu, Shida Liu,etal. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J]. Phys. Let，2001，A 289(1)：69-74.

[16]Zuntao Fu, Shikuo Liu, Shida Liu,etal. New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations[J].Phys. Lett，2001，A 290(1)：72-76.

(审稿人 王艳华 朱维佳，责任编辑 于 海)

Exact solution of (1+1)-D-Combination KdV-mKdV equation under the method of strengthening and improving the evolution equation

LIU Ming-quan

(Chaoyang Teachers College,Chaoyang Liaoning 122000)

To solve the evolution equation of higher dimension, the method of strengthening and improving evolution equation has been used to obtain the exact solutions of variable coefficient of nonlinear evolution equations, which can be further utilized to obtain the exact solution of (1+1)-D-Combination KdV-mKdV equations from which solitary-like solution and soliton solution can be resolved. The results showed that the method of strengthening and improving the evolution equation is a validate method to solve the exact solutions of nonlinear evolution equations in the field of mathematic and physics.

the method of strengthening and improving evolution equation; nonlinear evolution equations;exact solutions; solitary-like solution;soliton solution

2016—10—10

刘名权(1965-)，男(蒙古族)，辽宁朝阳县人，讲师，主要从事运筹学、图论等方面研究．

O175.2

A

1008-5688(2017)01-0001-05