城市高架桥塌落冲击地铁隧道结构的动态响应及防护技术
钟明寿, 龙 源, 刘 影, 路 亮, 刘健峰, 纪 冲
(1. 解放军理工大学 野战工程学院,南京 210007; 2. 中国人民解放军72351部队,山东 莱芜 271109)
城市高架桥塌落冲击地铁隧道结构的动态响应及防护技术
钟明寿1, 龙 源1, 刘 影1, 路 亮2, 刘健峰1, 纪 冲1
(1. 解放军理工大学 野战工程学院,南京 210007; 2. 中国人民解放军72351部队,山东 莱芜 271109)
利用ANSYS/LS-DYNA有限元软件对城市高架桥塌落振动及其对地铁隧道结构的影响进行了系统研究,建立了适于描述桥体塌落冲击作用下地铁隧道结构动力响应的三维有限元计算模型。通过比较有、无防护条件下桥体塌落冲击隧道结构动力响应过程,得到了不同工况下典型质点单元三向振动速度及应力时程曲线变化规律。研究结果表明,与无防护措施条件下桥体塌落冲击隧道结构相比,以“钢板-橡胶轮胎”为主要形式的复合防护结构使隧道所受的振动速度、压应力和拉应力最大值分别下降了98.7%、95.6%及94.4%。实测数据与数值计算结果具有良好的一致性,隧道结构所承受的振动速度低于地铁管理部门提出的安全阈值要求,综合防护体系设计达到了预期效果。
高架桥;塌落冲击;动态响应;防护;数值模拟
随着国民经济的迅猛发展及城镇现代化改造步伐的加快,拆除爆破技术以其施工周期短、劳动强度低及经济高效的优点在市政改建、扩建工程的应用越来越广泛[1]。然而,由于城镇地域空间相对狭小,拆除爆破在得到应用的同时也不可避免地带来一系列的负面效应,其中爆破地震效应被公认为这些破坏作用的公害之首[2],按产生机理其又可分为装药爆炸产生的爆破振动[3-4]及建(构)筑物触地瞬间引起的塌落振动两部分。大量工程实践表明,由于拆除爆破装药分布于建(构)筑物的各个支撑部位,空间分散,且各装药采用微差间隔技术控制起爆,使得爆破振动的危害性相对较小;而失去稳定的大体积、高重量拆除结构在触底瞬间将产生强大的冲击地压,并以应力波的形式向外传播;相关资料表明,塌落振动的主振频率与建(构)筑物的固有频率相当,且振幅较大、持续时间较长[5-7]。因此,与爆破振动相比,拆除爆破塌落振动对周边建(构)筑物及设施安全的影响将更大[8],尤其当爆区附近建(构)筑物较多、地下管线密布时,塌落振动极易对这些目标构成威胁。
近年来,针对拆除爆破塌落振动的研究主要集中在利用实验手段或测试技术分析塌落振动的传播规律及影响机理方面[9-10]。然而,随着拆除爆破工程的迫切需要及对塌落振动潜在危害的深入认识,对建(构)筑物在塌落振动作用下地下浅埋管件的动力响应[11]做出定性及定量分析,以便使拆除爆破技术朝着更为科学、可控的方向发展是广大工程技术人员迫切需要的。当前,建(构)筑物的抗震设计均以构造(天然)地震作用为依据,而塌落振动与构造地震波存在很大的时频特性差异[12]。因此,在爆破前事先对塌落振动对周边建(构)筑物结构的影响机理进行理论分析及安全评估,并将存在安全隐患的结构进行防护、加固处理,以确保待保护目标的安全稳定是非常有必要的。
本文以某市城西干道快速化改造工程为背景,利用ANSYS/LS-DYNA有限元软件建立适于描述高架桥塌落冲击地铁隧道结构的三维有限元模型,对桥体倒塌触地冲击作用下城市地铁隧道的动力响应进行数值仿真分析,并依据复合防护措施条件下隧道结构安全稳定性的数值计算,为综合防护体系的设计及爆破方案的优化提供进一步的借鉴和指导。
1 工程概况
高架桥作为一种典型建(构)筑物,研究其塌落冲击作用下浅埋管线动力响应过程具有十分重要的实际意义。本文以某市城西干道快速化改造过程的高架桥塌落冲击浅埋管线为研究对象,着重研究桥体塌落振动条件下浅埋管线及周围土体的动力响应过程。该高架桥主体结构呈南北走向,分别与汉中路、广州路相交,桥体两侧道路沿街房屋多为临界商铺和办公写字楼,距离最近处仅有6 m,周边环境示意图见图1。其中针对本次拆除爆破工程需重点保护的目标之一就是穿越高架桥14#墩地下15 m处正在运营的地铁2#线隧道。如图1所示,图中红线部分表示地铁隧道走向,黄线部分表示隧道上方待拆除的高架桥主体结构(13#~15#墩)。

图1 高架桥拆除爆破周边环境示意图Fig.1 Surroundings schematic diagram of blasting demolition
为确保高架桥塌落后,桥体结构触地冲击地面形成的塌落地震效应不会对隧道结构及地铁正常运营构成安全威胁,本文将采用仿真计算的方法对塌落冲击作用下隧道结构的动力响应进行数值分析,为优化城市高架桥体塌落冲击作用下地铁隧道结构动力响应及防护技术研究提供参考。
2 桥体塌落冲击隧道结构动力响应的数值分析
2.1 数值计算模型
实际工程中距离地铁较远的桥体倒塌触地产生的应力波对隧道结构及其设施的影响相对较小,因此,为减小计算量,本节重点考虑地铁隧道正上方的桥体部分,即13#~15#墩之间的桥体。由于高架桥桥体塌落触地后引起的地面振动是一个相对复杂的力学过程,为使问题简化,在误差允许的情况下本文对所建立的计算模型作以下假设:
假设1 研究所涉及的土体及高架桥混凝土材料均为连续且各向同性的均质材料;
假设2 高架桥塌落整体以自由落体的方式垂直冲击地面,不考虑其它阻力因素。
根据高架桥的实际尺寸,桥体模型长宽高尺寸分别设置为50 m×20 m×0.6 m,距地面高度为7.0 m;隧道衬砌支护层为50 cm厚的C50钢筋混凝土。根据地铁隧道实际尺寸,利用ANSYS/LS-DYNA有限元软件建立如图2所示的1/2高架桥-土体-隧道有限元计算模型。为模拟土体的半无限空间,约束对称面节点的法向位移和转动,并将模型侧面及底面设为透射边界。桥体添加自7 m处自由落体获得的速度载荷(11.7 m/s),为了清楚描述“高架桥-土体-隧道”动态响应过程,对于该系统均采用Lagrange网格和Solid 164实体单元进行有限元化,桥体、土体及地铁隧道的材料参数选择参考文献[13];为更加直观展现应力波在隧道结构中的传播过程,沿隧道衬砌内表面半环向均匀选取五个距地表不同深度h的特征单元,其分布模式如图2(b)所示。

图2 塌落振动有限元计算模型(1/2模型)Fig.2 Finite element model of collapse vibration of building (structure) conformation(1/2 model)
2.2 计算结果分析
研究桥体塌落振动的传播及其对地铁隧道的作用
过程,以桥体倒塌触地时刻为计时零点,设置整个计算时间长度为80 ms。计算得到桥体塌落触地应力波在土体及隧道结构中的传播过程如图3和图4所示。高架桥塌落触地时作用于土体的冲击载荷经土体介质再作用于隧道结构,应力波在土体中的衰减是由于波阵面

图3 应力波在土体中的传播过程Fig.3 Process of stress wave propagation in the soil
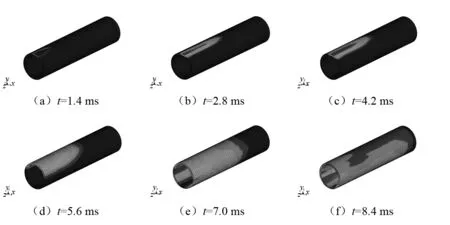
图4 应力波在隧道中的传播过程Fig.4 Process of stress wave propagation in the tunnel lining
面积不断增加引起的辐射衰减、介质内黏性内摩擦所产生的吸收衰减及冲击振动引起介质永久塑性变形所产生的衰减。因此,要想增大桥体塌落时载荷高速冲击土体介质后作用于隧道结构的速率,必须考虑具有一定刚度且具有良好吸能材料介质作为缓冲。
图5是隧道结构特征单元的振动速度时程曲线,从图中还可以看出,在高架桥塌落冲击荷载的作用下,隧道结构主要承受y向振动速度的影响,x向和z向振动速度相对较小;随着距离地表深度的增加,质点三向振动速度峰值均表现出逐渐减小的趋势。图6是隧道特征单元的应力时程曲线,从图中可以看出隧道上y向及z向的最大应力出现在边墙中心处,而该处x向的应力与隧道上的其它单元相比要小得多。
数值计算表明桥体塌落冲击中心,隧道结构的振动速度峰值出现在管道顶部(6.25 m/s),而有效应力最大值出现在隧道边墙上(压应力为43.7 MPa;拉应力为22.3 MPa)。在此条件下,桥体塌落振动作用下地铁隧道结构所承受的振动速度及有效应力远远不能满足隧道结构的安全阈值[14]要求,地铁隧道处于极度危险中。
因此,桥体塌落冲击地铁隧道动态响应幅值较大,针对埋地管线进行适当的减震防护措施是必要的,本文拟在预塌落区域地面铺设一种复合减震结构,从而达到吸收桥体塌落冲击能量、保护埋地管线的目的。
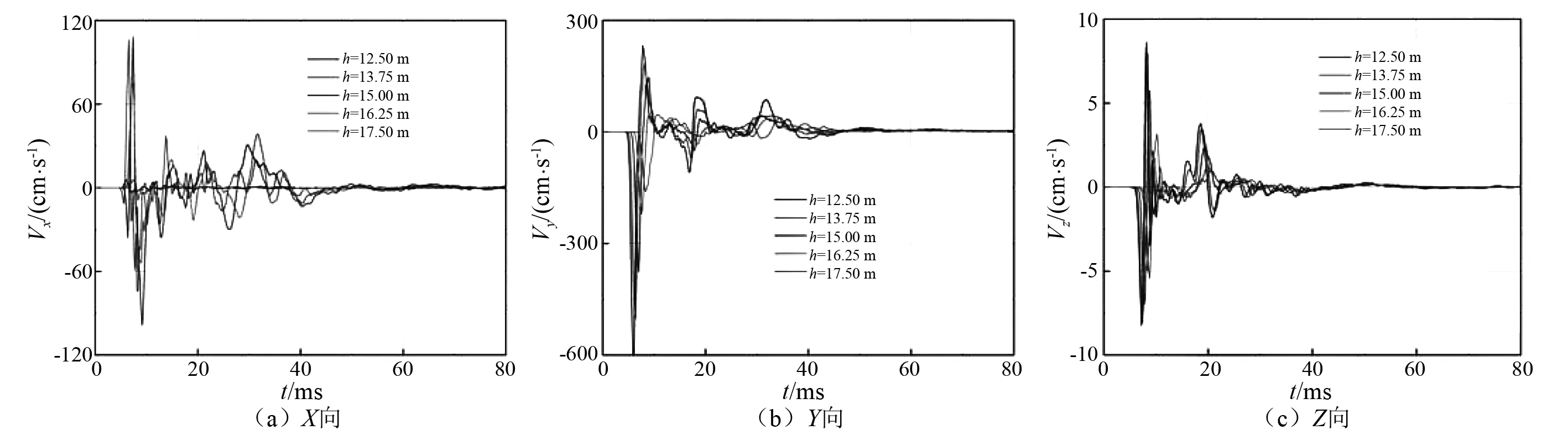
图5 隧道特征单元振动速度时程曲线Fig.5 Vibration velocity-time curve of typical units in the tunnel lining

图6 隧道特征单元应力时程曲线Fig.6 Vibration stress-time curve of typical units in the tunnel lining
3 有防护措施下城市隧道结构安全稳定性的数值分析
3.1 数值计算模型
在无防护措施的条件下,数值计算结果表明高架桥塌落触地对地面的冲击荷载极有可能对隧道结构的稳定性构成威胁。因此,为切实确保地铁隧道的正常运营,根据以往理论计算[15]和类似爆破工程减震措施的经验[16],项目部优化设计了爆破拆除方案及综合防护体系[17],从而达到吸收塌落桥体冲击能量、保护埋地管线的目的。为提高数值计算效率,本文着重针对综合防护体系中的“钢板-橡胶轮胎”复合防护结构进行研究。
按照2.1节中的基本假设及相应参数建立如图7所示的有防护措施的塌落振动计算模型,其中,钢板-橡胶轮胎复合防护结构的局部放大模型如图8所示,钢板及橡胶轮胎的材料参数均取自参考文献[13]。

图7 有防护措施的塌落振动计算模型(1/2模型)Fig.7 Finite element model of collapse vibration of building (structure) conformation with protective measures(1/2 model)

图8 钢板-橡胶轮胎复合防护结构模型图Fig.8 Schematic diagram of steel plate-rubber tires system
3.2 计算结果分析
高架桥桥体塌落首先与橡胶轮胎发生碰撞,设初始碰撞时刻为计时零点,计算时间为80 ms。图9为各特定时刻橡胶轮胎中应力波的传播及受桥体冲击的变形情况。当t=25 ms时,橡胶轮胎受冲击后竖向变形已达到17.46 cm,由此可知,由于防护结构的缓冲作用,高架桥桥体塌落过程释放的位能部分转换为橡胶轮胎的变形能,从而能够减弱对土体介质的直接冲击作用。
图10是应力波在土体中的传播过程,从图中可以看出,桥体的冲击能量通过复合防护措施的缓冲后,作用于地表土体的能量与图3相比已大幅衰减;图11是应力波在隧道结构中的传播过程,通过图11可以发现,
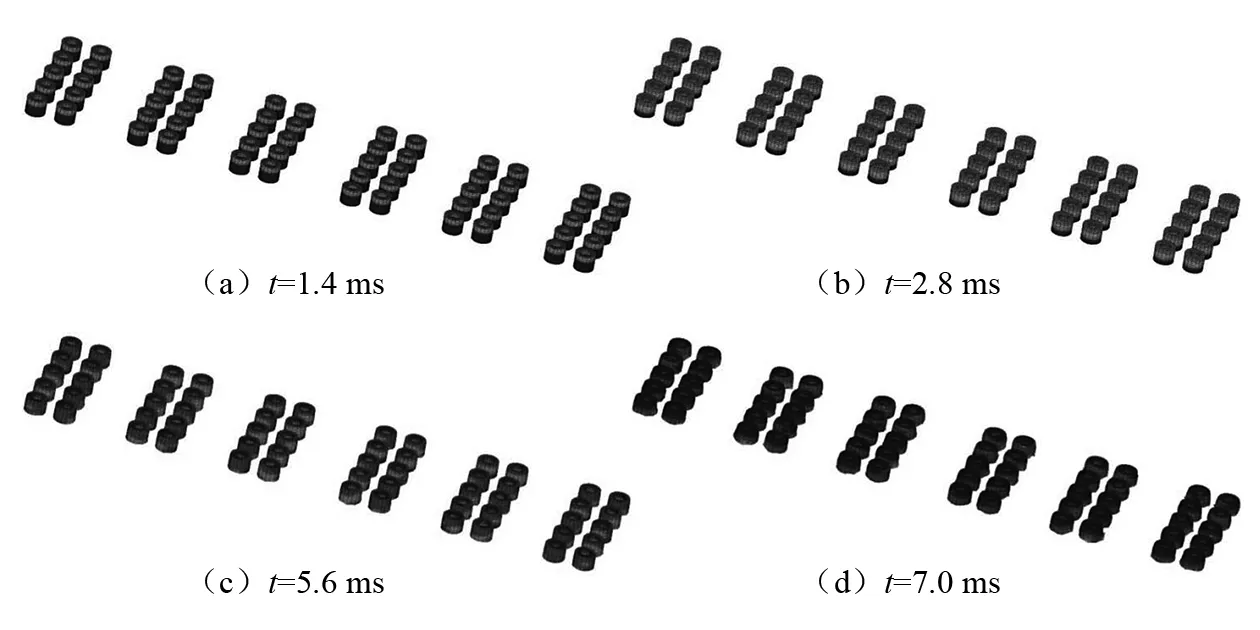
图9 橡胶轮胎受桥体冲击后的变形情况Fig.9 Deformation of the tire rubber under collapse vibration
拱顶至边墙中心之间的隧道所承受的应力峰值较大,且持续时间较其他位置也要长得多。出现这种现象的主要原因是由地面防护结构的摆放与隧道结构的空间相对位置引起的,隧道侧面正上方的两组橡胶轮胎将更多的应力波能量直接作用于上部边墙位置的隧道结构,因此,防护措施的合理设计对应力波在土体中的传播及其对隧道结构的作用过程至关重要,只有合理匹配防护结构的摆放与隧道位置的关系才能确保隧道结构的安全稳定。
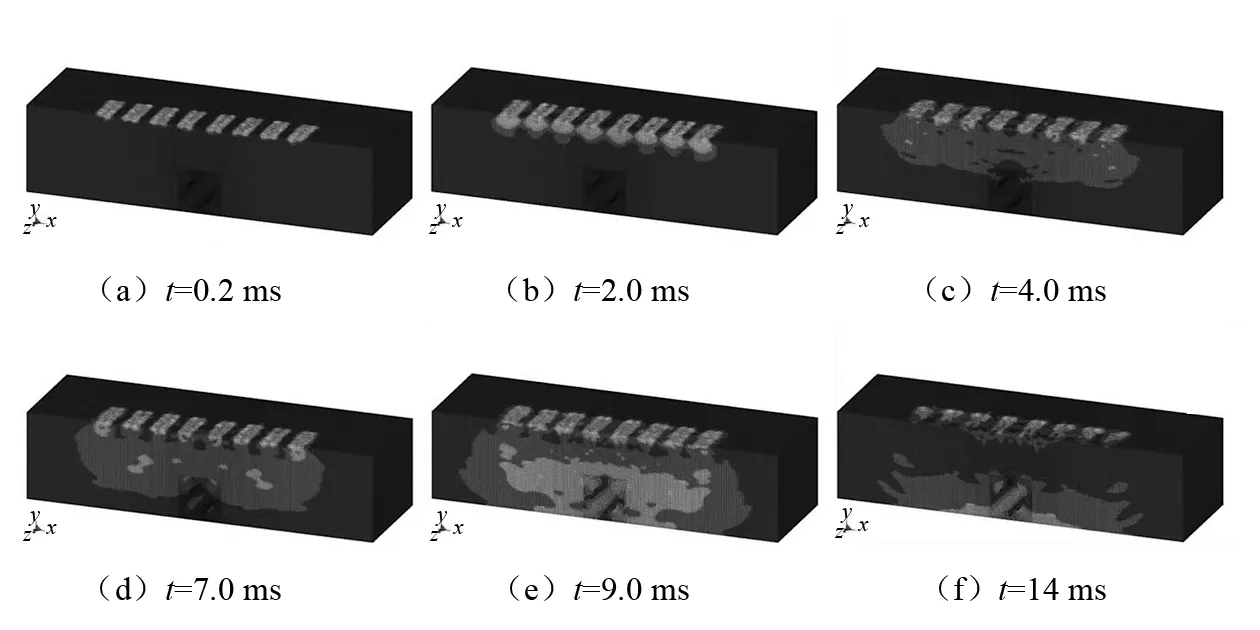
图10 应力波在土体中的传播过程Fig.10 Process of stress wave propagation in the soil

图11 应力波在隧道中的传播过程Fig.11 Process of stress wave propagation in the tunnel lining
按照图2(b)所示的位置在有防护措施的计算模型中选取距地表不同深度h的土体及隧道结构特征单元,通过计算分别得到如图12所示的振动速度时程曲线及如图13所示的应力时程曲线。
通过与图5和图6中无防护措施条件下隧道特征单元的振动速度时程曲线、应力时程曲线的对比可知,钢板-橡胶轮胎组合防护结构对高架桥桥体的冲击起到了较好的缓冲作用,隧道结构中的振动速度峰值、应力峰值得到极大幅度的衰减。其振动速度最大值(8.25 cm/s)出现在拱顶处,压应力最大值(1.94 MPa)出现在边墙上,而拉应力最大值(1.25 MPa)出现在底板上,与无防护措施条件下的对应值相比分别下降了98.7%、95.6%及94.4%,由此可见,采用复合结构的防护措施可以有效降低高架桥桥体塌落时产生的位能向土体及隧道结构中传递的百分比,能够达到保护隧道结构、确保地铁正常运营的目的。

图12 隧道特征单元振动速度时程曲线Fig.12 Vibration velocity-time curve of typical units in the tunnel lining

图13 隧道特征单元应力时程曲线Fig.13 Vibration stress-time curve of typical units in the tunnel lining
4 工程实测结果分析
高架桥桥体拆除爆破工程实际操作中,为充分保证桥体下方地铁隧道的安全稳定性,在对有防护措施进行数值计算的基础上,对地铁隧道的不同位置进行了桥体塌落冲击震动数据监测。爆破振动测点的布置包括监测点个数与传感器设置位置两个内容。相关研究表明,邻近爆炸载荷作用下隧道周边振动场分布特点是最大振动速度出现在隧道迎爆侧的墙壁和拱部,墙脚点振动速度较小,背爆侧振动相对较轻。由于地铁隧道上部为供地铁运行的电力设备,根据试验结果地铁轨道底部振动较小,因此将测点分别选取在迎爆侧位于隧道侧壁上、中和下三处。测点的具体布置如图14所示,分别在距离地铁隧道底部3.5 m, 2.5 m 和1 m处布置测点1#, 2#和3#。为了避免地铁隧道中列车运行产生的振动误触发爆破测振仪,触发值设置为0.5 cm/s。
图15是地铁隧道不同位置处三向振动速度时程曲线的监测值。从图中可以看出,在高架桥塌落冲击荷载的作用下隧道结构承受Y向的振动速度幅值最大,因此,基于对地铁隧道类浅埋管线结构的保护要着重考虑建(构)筑物直接受冲击方向的塌落冲击危害效应,这与数值计算结果是一致的;靠近隧道结构顶部的振动速度较大,1#测点的最大振动速度为-3.12 cm/s,沿隧道顶部到底部逐渐减小,2#、3#测点的最大振动速度分别为-2.00 cm/s、0.75 cm/s;实测振动波形由初始爆破地震波和桥体塌落振动产生的地震波叠加而成,爆破地震波幅值相对桥体塌落震动产生的地震波幅值较小,可以忽略,符合数值计算的基本假设条件;桥体塌落振动引起地铁隧道动态响应时间较长,这主要是由爆破拆除高架桥的过程中采用的综合防护体系不仅仅限于“钢板-橡胶轮胎”复合防护结构、桥体塌落过程中触地时间不一致产生多次振动效应等因素造成的。
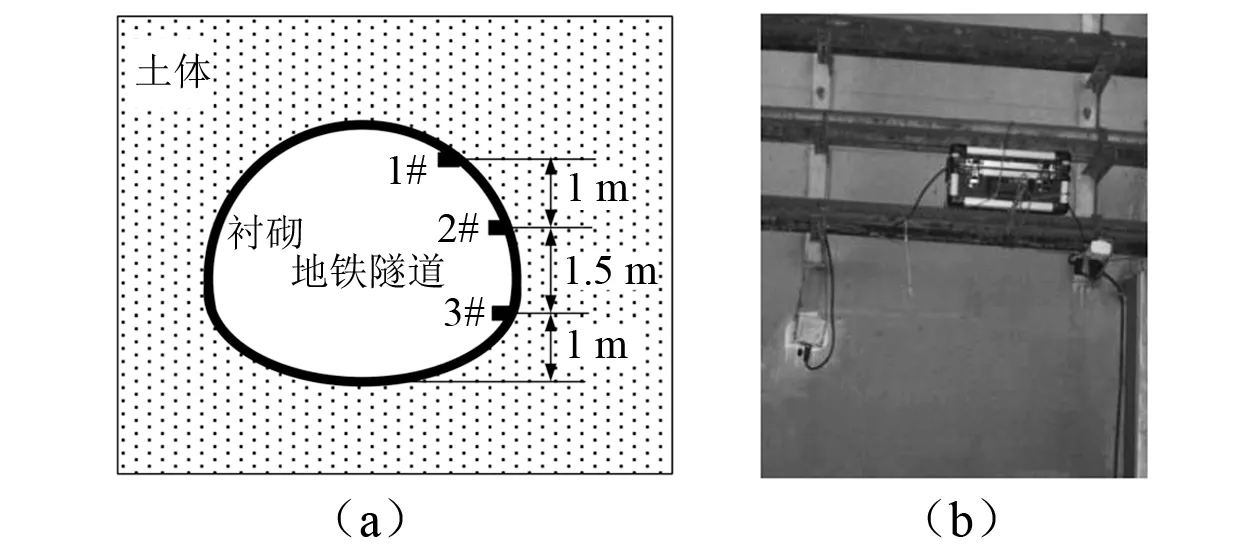
图14 地铁隧道不同位置测点布置示意图Fig.14 Schematic diagram of typical units in the tunnel lining
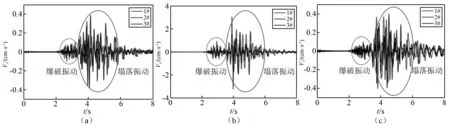
图15 隧道不同位置振动速度时程曲线Fig.15 Vibration velocity-time curve of typical units in the tunnel lining
高架桥塌落及钢板-橡胶轮胎复合防护结构变形情况如表1所示。从表中可以看出高架桥爆破拆除的数值计算结果与工程爆破结果吻合较好,说明利用有限元分析的方法对拆除爆破塌落冲击作用下城市隧道的动力响应及防护措施进行研究是非常有效的,能够为类似工程中评估爆破方案的可行性及防护措施提供有力的技术支撑。
本工程实例应用中所选择的综合防护系统既有一定的“刚性”,又要有一定的“柔性”,刚柔相济穿插进行,从而达有效削减塌落桥体的冲击动能进而保护地下浅埋管线结构的目的。如应用橡胶轮胎作为一种柔性结构在承接塌落冲击载荷的同时能产生一定的变形(弹性或弹塑性变形)来有效削减塌落桥体的直接冲击动能,达到保护目标的结果。而钢板作为一种刚性结构可以将桥体塌落冲击载荷在自身发生较小变形幅值条件下均匀作用于地面,结合橡胶轮胎组成具有一定刚度的柔性材料或柔性结构来接载、缓冲、消能,减小对地面及其地下浅埋管线的震动影响。因此工程中所选取的钢板加橡胶轮胎的复合结构,其竖向有一定的刚度和弹性,侧向又有一定的抗剪切变形的能力。综合防护系统的接载和消能效果明显。
高架桥爆破拆除塌落过程中,经过综合防护体系及地铁隧道表面浅埋土体的作用,塌落桥体冲击地面产生的地震波幅值已产生大幅度的衰减。对地铁隧道的实测数据显示,隧道结构所承受的振动速度低于地铁管理部门提出的安全阈值要求,且经专业部门检查评估,地铁隧道结构及其内部设施均完好无损,爆破方案及防护体系设计达到了预期效果。

表1 高架桥桥体塌落及钢板-橡胶轮胎复合防护结构变形情况
5 结 论
(1) 通过有效模型简化和假设,建立了城市高架桥塌落冲击作用下地铁隧道结构动力响应的数值计算模型,研究了桥体塌落冲击地面产生应力波在土体及隧道中的传播规律特征。
(2) 针对有(无)防护措施条件下隧道结构安全稳定性进行了数值计算,研究结果表明以“钢板-橡胶轮胎”为主要形式的复合防护结构使隧道所受的振动速度、压应力和拉应力最大值分别下降了98.7%、95.6%及94.4%;桥体塌落冲击地铁隧道结构的工程实测结果进一步证明以数值计算为基础深入优化的爆破方案及综合防护体系能够确保高架桥塌落冲击作用下地铁隧道结构及设施的安全稳定。
(3) 利用有限元分析的方法对拆除爆破塌落冲击作用下城市隧道的动力响应及防护措施进行研究是非常有效的,能够为类似工程中评估爆破方案的可行性及防护措施的有效性,从而改进工程实施计划提供有力的技术支撑。
[ 1 ] HACK A. Latest developments in tunneling technology and their perspectives [J]. Tunnel, 2002, 10: 4-6.
[ 2 ] 汪旭光,于亚伦.21世纪的拆除爆破技术[J].工程爆破,2000, 6(1):32-35. WANG Xuguang, YU Yalun. Demolition blasting technology faced with the 21 century [J]. Engineering Blasting, 2000, 6(1):32-35.
[ 3 ] MA G W, HAO H, ZHOU Y X. Modeling of wave propagation induced by underground explosion [J]. Computers and Geotechnics, 1998, 22(3/4): 283-303.
[ 4 ] HAO H, WU Y K, MA G W, et al. Characteristics of surface ground motions induced by blasts in jointed rock mass [J]. Soil Dynamics and Earthquake Engineering, 2001, 21(2): 85-98.
[ 5 ] 龙源, 娄建武, 徐全军. 爆破拆除烟囱时地下管道对烟囱触地冲击振动的动力响应[J].解放军理工大学学报,2000,4(2): 38-42. LONG Yuan, LOU Jianwu, XU Quanjun. Subterranean pipeline’s dynamic response to ground shock caused by demolished chimney[J]. Journal of PLA University of Science and Technology, 2000, 4(2): 38-42.
[ 6 ] 罗艾民.高耸筒式构筑物控制爆破拆除研究[D].西安:西安科技学院,2001.
[ 7 ] 王希之, 王自力, 龙源, 等.高层建筑物爆破拆除塌落震动的数学模型[J].爆炸与冲击,2002,4(2): 188-192. WANG Xizhi, WANG Zili, LONG Yuan, et al. A mathematical model of collapse vibration in blasting demolishing tall buildings[J]. Shock and Wave, 2002,4(2):188-192.
[ 8 ] 叶洲元, 马建军.爆破拆除高耸建筑物触地危害分析与控制[J].中国安全科学学报,2010,20(2):150-154. YE Zhouyuan, MA Jianjun. Harm analysis of collapse and touchdown of tower buildings in demolition of blasting and its control measures[J]. China Safety Science Journal, 2010,20(2):150-154.
[ 9 ] HAO Hong, MA Guowei, LU Yong. Damage assessment of masonry in filled RC frames subjected to blasting induced ground excitations[J]. Engineering Structures, 2002, 24(6): 799-809.
[10] WU Chengqing, HAO Hong, LU Yong. Numerical simulation of structural responses on a sand layer to blast induced ground excitations[J]. Computers and Structures, 2004, 82(9/10): 799-814.
[11] 杨永强,胡进军,谢礼立,等.沌阳高架桥爆破拆除塌落引起的地面振动特征[J].振动与冲击,2015,34(5):110-114. YANG Yongqiang, HU Jinjun, XIE Lili, et al. Characteristics of ground vibration caused by blasting demolition collapse of zhuanyang viaduct[J]. Journal of Vibration and Shock,2015, 34(5):110-114.
[12] 姚琼. 建筑物爆破拆除塌落振动作用下周边结构的安全性分析田[D]. 武汉:武汉理工大学,2007.
[13] 路亮. 爆破荷载作用下城市隧道结构动力分析及安全判据研究[D]. 武汉:解放军理工大学, 2014.
[14] 培契曼 H,艾曼 W. 人和机械引起的结构振动[M].李直仓, 李文远, 译. 北京:建筑科学编辑部,1990.
[15] 李兴华,龙源,纪冲,等. 爆破地震波作用下隧道围岩动应力集中系数分析[J].岩土工程学报,2013,35(3):578-582. LI Xinghua, LONG Yuan, JI Chong, et al. Dynamic stress concentration factor for tunnel surrounding rock under blasting seismic waves[J]. Chinese Journal of Geotechnical Engineering,2013,35(3): 578-582.
[16] 李兴华,龙源,钟明寿,等.哈尔滨龙海大厦拆除爆破中的减振技术研究[J]. 爆破器材, 2009, 38(6): 30-32. LI Xinghua, LONG Yuan, ZHONG Mingshou, et al. Study on technology of vibration reduction in demolition blasting of long hai mansion in haerbin[J].Explosive Materials,2009,38(6):30-32.
[17] 龙源,季茂荣,金广谦,等. 南京城西干道高架桥控制爆破与安全防护技术[C]∥ 第十届全国工程爆破学术会议.北京:工程爆破,2012:602-613.
Dynamic response and protection technology research onmetro tunnels under collapse vibration of city viaduct
ZHONG Mingshou1, LONG Yuan1, LIU Ying1, LU Liang2, LIU Jianfeng1, JI Chong1
(1. College of Filed Engineering, PLA University of Science and Technology, Nanjing 210007, China;2. 72351 Troops, PLA, Laiwu 271109, China)
The collapse vibration performance laws of city viaducts to metro tunnels were obtained by using ANSYS/LS-DYNA software. The calculation model of collapse bridge impact to the underground tunnels of cities was established. Dynamic response of a metro tunnel including three-direction vibration velocity and stress process of typical units was also obtained. The results show that as a main form of composite protective structure consisting of a steel plate-rubber tires system can make maximum of metro tunnel vibration velocity, compressive stress and tensile stress were decreased by 98.7%, 95.6%, and 94.4% compared with the absence of protective measures. It has shown excellent agreement between measured data and simulation results. Metro tunnel borne vibration speed is lower than the administration proposed safety threshold requirement and the design of comprehensive protection system achieves the expected result.
viaduct; collapse vibration; dynamic response; protection; numerical simulation
城市桥梁拆除爆破塌落振动对市政管线的损伤机理和安全判据研究(51508569);爆破振动危害效应远程监测机理及减振策略研究(BK20151449);基于能量原理的碳酸盐岩激发机理研究(51304218)
2016-03-02 修改稿收到日期: 2016-06-28
钟明寿 男,博士,讲师,1983年生
刘影 女,博士,副教授,1975年生
O329
A
10.13465/j.cnki.jvs.2017.16.002

