以带肋楼板为质量块形式的TMD设计方法研究

裴星洙， 孙健杰

(1. 江苏科技大学 土木工程与建筑学院，江苏 镇江 212003; 2.上海二十冶建设有限公司，上海 201999)

以带肋楼板为质量块形式的TMD设计方法研究

裴星洙1， 孙健杰2

(1. 江苏科技大学 土木工程与建筑学院，江苏 镇江 212003; 2.上海二十冶建设有限公司，上海 201999)

为了不额外增大结构自重，同时又能将TMD原理很好的应用于高层建筑结构地震反应控制，提出以带肋楼板的恒载和活荷载换算为子结构的质量、设置在主梁(包括次梁)和带肋楼板之间的橡胶隔震垫的抗侧刚度和阻尼代替子结构的弹簧和阻尼器的一种TMD体系。考虑该TMD的高层建筑为研究对象，建立振动微分方程，利用自编程序进行地震反应弹塑性时程分析，讨论该体系的合理性和可行性。基于定点理论的思想对TMD的设计方法进行研究。在多种地震动作用下，分别计算原结构与消能减震结构的地震反应，并对比两者的耗能情况。考虑TMD设置位置对消能结构地震反应的影响，分析该TMD在实际工程中实施的可行性和方案，最终提出简单有效的TMD设计方法-定点理论修正法。基于该方法并运用算例模型进行计算分析，结构运用该方法后具有较好的消能减震效果，故定点理论修正法是合理可靠的。

调谐质量阻尼器；设计方法；地震响应；能量关系

近些年，大地震和风荷载造成的损失越来越严重，人们也意识到传统结构对自然灾害抵御能力的局限性。研究表明合理有效的减震途径是对结构附加控制装置形成消能减震结构。作为一种被动控制装置，由弹簧、阻尼元件和质量块所组成的质量调谐阻尼器(Tuned Mass Damper， TMD)具有很大的优越性，该装置在高层和高耸结构的抗风控制中具有广阔的应用前景，目前已经有不少高层建筑成功运用了该装置来进行减振控制，比如美国波士顿 John Hancock 大楼在顶部安装了两个 300 t 的TMD；台北的101大楼在第87～92层装配了一个重660 t的TMD，其减振效果都很明显[1]。

基于目前对TMD减震系统的研究可知，子结构的质量越大，其减震效果越好，故一般都是在结构顶部额外安置重型质量块，因而同时也会使结构上部自重增大、引起p-△效应，不利于抗震。为了不额外增大结构自重，同时又能将TMD原理很好的应用于地震反应控制，专家学者对此做了不少的研究。

徐家云等分析了屋顶花园作为TMD的减震机理，并对TMD的参数进行最优设计，并利用一小高层算例验证了其可行性与有效性。王磊等针对广州某国际大酒店的加固改造工程为背景，将其顶上布置的水箱为质量块设计TMD。田志昌设计了一种滑动屋盖系统，并将其作为隔震吸振装置，对一框架结构进行了算例分析，发现结构的最大侧移、最大层间位移减少能达到45%。翁大根等运用滑动橡胶支座设计出了一种楼面隔震装置，并进行了振动台实验。冼巧玲等提出了楼板隔震消能结构体系，分析了结构参数对其传递函数的影响、对结构参数进行了优化，并进行了单层楼板隔震消能结构体系的振动台试验研究，得出该体系能很好的减小结构加速度和底部剪力的结果。韦长庚提出了室内设施隔震-房屋结构减震体系，主要探讨了室内设施隔震系统的阻尼比，质量比，位移传递函数对其减震效果的影响，并对该系统的各参数进行优化分析得到最优参数。

在文献[2-3]中，将子结构设置在结构的顶部，而本文将子结构设置在结构某些层；在文献[4]中以屋盖、摩擦材料、弹簧板形成滑动屋盖系统，在文献[5]中利用楼板形成隔震系统并进行振动台试验，在文献[6-7]中主要讨论子结构各参数对传递函数的影响，是属于理论分析，而本文提出以带肋楼板的恒载和活荷载换算为子结构的质量、以铅芯橡胶隔震支座的等效抗侧刚度和等效阻尼作为子结构的弹簧和阻尼器，从而形成的一种新的TMD(子结构)，讨论其实际工程中的实施可能性和减震效果，并归纳设计方法为工程设计提供参考。

1 主结构与子结构的平面及空间构造

本文选用附加子结构的12层钢框架结构进行分析，纵向方向共6跨，其跨度为6.4 m；横向方向共3跨，其跨度为9.6 m，底层层高5.0 m，其余各层层高均为4.0 m，其建筑平面和立面如图1所示。当地震动来临时，为了避免质心和刚心不重合而发生的扭转变形，将子结构布置在结构平面对称位置上(在图1(a)中，以虚线表示的部分为子结构)，并加强支撑子结构(在图1(b)中，横梁上Ⅱ型部分)的横梁和柱子的强度，保证其正常工作。

柱子截面采用箱型截面(除4个角柱为C1外，其余全为C2)，梁截面采用H型截面(平面图上纵向方向的梁为G1、横向方向的梁为G2表示)，其尺寸见表1和表2。梁柱节点采用固结方式连接，钢材牌号为Q345，其弹性模量为200 GPa。设结构各层质量相同，均为1 000 kg/m2，则每一层的质量为1 105 920.0 kg。

图1 算例模型(单位：mm)Fig.1 Calculation model (unit: mm)

层数C1C21□600×600×25□600×600×282～4□600×600×22□600×600×255～8□550×550×22□550×550×259～12□500×500×19□500×500×22

表2 梁截面尺寸

利用snap软件对三维空间结构进行推覆分析，得到如图2所示层剪力-位移曲线。本文将各层的骨架曲线简化为标准的三线型恢复力模型，则其各层的恢复力特性参数如表3所示。其中，Up1、Up2分别为第一、第二屈服位移，Sk1、Sk2、Sk3分别为弹性刚度和第一、第二屈服刚度。

图2 恢复力-位移曲线Fig.2 Restoring force-displacement curve

层数Up1/mUp2/mSk1/(N·m-1)Sk2/(N·m-1)Sk3/(N·m-1)10．03580．04701．45E+0083．43E+0073．71E+00520．04150．05001．22E+0083．88E+0079．98E+00630．04580．06231．12E+0089．70E+0065．82E+00640．04400．06201．10E+0081．44E+0075．55E+00650．04530．05009．71E+0078．09E+0077．02E+00660．04350．05009．52E+0075．08E+0071．49E+00770．04180．04908．86E+0076．62E+0072．86E+00680．03750．04128．75E+0077．57E+0071．90E+00790．03830．04107．22E+007--100．03320．03526．51E+007--110．02650．02805．74E+007--120．01800．01904．44E+007--

2 子结构

2.1 子结构形成机制与设置楼层

本文所提出的子结构与目前已经应用的子结构形成机制有所不同。其主要区别在于，本文研究的TMD不设专门的质量块，而是在建筑结构某一层两根框架次梁的交界处顶上摆放铅芯橡胶隔震支座，并在其上方布置带肋梁的楼板(见图1)。由肋梁、楼板的自重和正常使用时的活荷载换算得出子结构的质量，以铅芯橡胶隔震支座的抗侧刚度和阻尼代替子结构的弹簧和阻尼器，从而形成一个新的子结构形态。

考虑减震效果和经济效应(包括施工周期)，在结构振动振型中，选择影响度较高的前几阶振型为减震对象，通过分析得知前几阶振型最大振幅出现的楼层后，就在该层对称位置上布置上述的子结构(见图1)。

2.2 子结构的设置方法及侧向防撞措施

以12.8 m×9.6 m房间(见图1(a))为例说明其子结构设置方法。作为子结构的楼板下肋梁截面尺寸取为250 mm×250 mm(以布置井字形肋梁为例)。从框架交叉次梁顶面开始算起，橡胶支座上下连接板厚32 mm、橡胶支座净高度106 mm(以LRB300支座为例)、井字形肋梁高度250 mm、楼板厚度100 mm，则总高度为106 mm +250 mm +32 mm +100 mm =488 mm(见图3)。除底层外每层层高均为4.0 m，则设置子结构房间的有效高度为3 512 mm，充分满足正常使用所需要的高度。此外，在设置子结构的房间门口(房间内)设置2阶台阶，可以解决房间内楼板高度大于走廊高度的问题。为了保证发生地震时子结构的正常工作，楼板与房间四周、楼板与台阶之间各空出300 mm空间。空隙上方使用盖板(采用耐久性好、防火、隔声、隔热的柔性材料制成)覆盖并搭接在楼板上,正常使用时盖住空隙，且能保证房间的美观洁净，在发生地震时柔性盖板易变形且不会阻碍子结构的振动。

当地震动很强时，隔震垫上部“质量块”的水平位移过大，会引起隔震垫两侧由受压状态变成一侧受压、一侧受拉的状态，导致“质量块”与柱子相互碰撞的现象。作为侧向防撞措施，在每个螺帽与连接板之间装设碟形弹簧(见图3)，发生很强的地震时，让受拉侧的蝶型弹簧在竖向方向上发生变形消耗部分能量的同时重新调整这一体系中的受力分布，达到避免碰撞。此外，在柱子临近“质量块”一侧的表面粘贴刚度和黏性适当的黏弹性材料板块(高度大于“质量块”板厚)，借用黏弹性材料板块一旦碰撞就吸收和储存能量的功能来实现“软碰撞”(见图4)，以便更好的保护主体结构和子结构。

图3 橡胶支座安装示意图Fig.3 Rubber bearing installation diagram

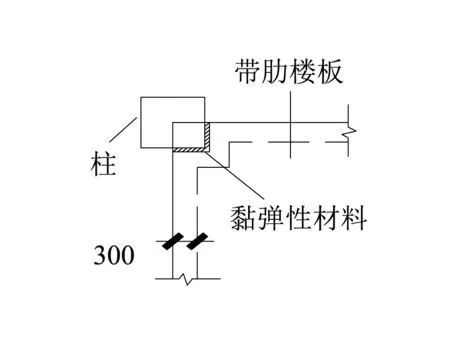
图4 楼板设计示意图Fig.4 Floor design diagram

2.3 子结构的质量、抗侧刚度和阻尼

以12.8 m×9.6 m房间(见图1(a))为例计算其子结构质量。楼板的有效面积大致为(6 400×2-300×2)×(9 600-600)-(1 300×600)×2=108.24 m2，其中(1 300×600)×2为上述的台阶所占的面积(考虑两扇门)。其中楼板厚度为0.1 m，混合砂浆抹灰厚度为20 mm，水泥砂浆面层厚度为25 mm，则楼板的总自重为(0.1×25+0.02×17+0.025×20)×108.24=361.52 kN。梁的自重引起的线荷载为0.25×0.25×25=1.563 kN/m，故井子梁总自重为2×(9.6+12.8)×1.563=70.02 kN，则总自重为361.52+70.02=431.54 kN，其中20 kN/m3、17 kN/m3、25 kN/m3分别为水泥砂浆、混合砂浆和钢筋混凝土的容重[8]。如果房间用作贮藏室，则活荷载为108.24×5.0=541.2 kN，其中5.0 kN/m2为活荷载标准值。总荷载为431.54+541.2=972.74 kN，将这一荷载换算为子结构的质量，则其大小相当于m=97 274.0 kg。

基于子结构的重量和所需抗侧刚度，查询橡胶隔震支座相关参数表[9]，确定铅芯橡胶隔震支座的型号和数目以及等效阻尼比。

3 定点理论简介

讨论单质点体系的时候，与不同阻尼比对应的振动反应-频率比曲线具有两个定点Q和P。定点理论认为，当Q和P点的高度相等、且Q和P点周围没有比这两点更高的点的时候其减振效果最好。最佳谐振条件和阻尼条件分别为

(1)

(2)

式中：ωn，Ωn分别为子结构和主结构的固有圆频率；γ为频率比；μ为子结构与主结构的质量比；ζ为子结构的阻尼比。

讨论多质点体系的时候，在一般的情况下，往往将结构前几阶振型作为减震对象，与第i阶振型对应的等效质量Mi和Ki等效刚度为

(3)

(4)

式中：[M]、[K]为主结构质量矩阵和刚度矩阵；{Φ}i为第i阶振型向量。

第i阵型目标阻尼比ξei与质量比μi之间存在如下关系

(5)

利用式(6)、式(7)、式(8)，可确定与第振型对应的子结构质量、刚度以及阻尼。

mdi=μiMi

(6)

(7)

(8)

至于如何确定目标阻尼比ξei，作者在相关文献中没有见到具体方法。本文根据文献[10]中的目标阻尼比算例，通过分析与考察提出式(9)。

ξei=0.006 8i2-0.050 3i+0.137 5

(9)

式中，i为振型。

图5表示振型与目标阻尼比和目标阻尼比与质量比的关系。从两条曲线的具体大小和趋势来看，式(9)是合理的。

图5 目标阻尼比和质量比Fig.5 Target damping ratio and mass ratio

4 振动微分方程及子结构优化设计

4.1 振动微分方程

本文主结构采用质点系振动模型(见图1)，附加子结构的第层的受力分析见图6。主结构的第i层设置子结构，则该层的振动微分方程为

(10)

设置在主结构第i层上的子结构振动方程为

(11)

主结构其余各层j(除底层)的振动微分方程为

(12)

底层的振动微分方程为

(13)

本文采用上层上位的方式组装质量、刚度及阻尼矩阵。

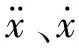
图6 TMD受力分析Fig.6 Stress analysis of TMD

4.2 优化设计

众所周知，除了超高层以外的建筑结构在水平地震作用下的振动中低频阵型起主要作用。作为优化设计的一道途径，本文把12层结构的前三阶振型作为减震对象。通过对前三阶振型的分析可知，一阶、二阶和三阶振型的最大振幅各出现在第12层、3层和7层(见图7参与向量，即阵型向量乘上参与系数的向量)，故子结构应该设定在第12层、3层和7层的楼订上。而本文在计算子结构质量时主要考虑带肋楼面板，故依据一阶振型而设置的子结构设定在第12层的楼面上，依据二，三阶振型而设置的子结构分别设定在第3层、7层的楼顶上。具体布置如图1所示。

由于本文提出的子结构形态与传统的子结构有所不同，为使附加该子结构的结构具有较好的减震性能，找出理想的子结构参数后要进行优化设计。以下分别采用三种子结构设计方法，通过地震反应弹塑性时程分析，选取优化设计方法。

图7 参与向量Fig.7 Participation vector

4.2.1 定点理论设计方法

由式(9)可求得与前三阶振型对应的目标阻尼比分别为

ξe1=0.094ξe2=0.064ξe3=0.048

由式(5)求得质量比分别为

μ1=0.073μ2=0.033μ3=0.019

表4为利用式(6)、式(7)、式(8)计算得到子结构质量、刚度以及阻尼系数。

表4 定点理论设计参数

按照本文2.3节提出的质量计算方法，若选用6.4 m×9.6 m, 12.8 m×9.6 m和19.2 m×9.6 m的房间(均用作储藏室)作为子结构，并考虑对称性，则对应子结构质量分别为94 471.2 kg、194 548.0 kg、294 626.0 kg。其中质量的最大值也远远小于表4中子结构质量的最大值，只占定点理论所需质量的33.2%，故很难满足定点理论所需的质量。本文基于工程的实际情况，对设计参数进行修正。作为工程设计方法可以考虑如下两种简易的设计方法。第一种设计方法是基于实际工程情况计算得到子结构质量以后，根据规范规定的橡胶支座的压应力限值，确定所需隔震支座的型号与数目，查表即可得到抗侧刚度及阻尼比；第二种设计方法是基于实际工程情况计算得到子结构质量以后，按定点理论的方法来计算抗侧刚度和阻尼系数。如下举例说明。

4.2.2 第一种设计方法

将12.8 m×9.6 m房间作为子结构体系。参考西安达盛隔震技术有限公司生产的铅芯橡胶支座，选用有效直径为300 mm的铅芯支座(LRB300)，查表可知单个支座的等效水平刚度为1 017 kN/m，屈服强度为24 kN，第一屈服位移为0.0236 m，等效阻尼比为0.255。表5为第12层、7层、3层每层选取两个12.8 m×9.6 m房间(活荷载标准值为5.0 kN/m2)、布置8个LRB300的铅芯橡胶隔震支座(每个房间布置4个)并基于第2.3节的计算方法得到的子结构参数。

表5 第一种设计参数

4.2.3 第二种设计方法

将12.8 m×9.6 m房间当作子结构体系，则子结构质量为194 548.0 kg。等效质量已知，故由式(6)可得如下质量比。

μ1=0.024μ2=0.029μ3=0.025

再利用式(7)、式(8)计算刚度和阻尼系数，可得表6所示设计参数。

表6 第二种设计参数

4.2.4 地震反应比较

基于表4～表6的设计参数，利用威尔逊θ法自编求解振动微分方程的电算程序[12]，采用EL CENTRO波、 KOBE波、ART ELCENTRO波、ART HACHINOHE波(加速度峰值均为400 cm/s2，时间间隔为0.01 s，作用时间为50 s)，进行地震反应弹塑性时程分析。图8表示最大位移；图9表示最大加速度。从图8中可以看出，上述基于三种设计参数的减震效果(绝对位移)在结构下部几乎相等，结构上部基于定点理论设计的效果更好。比较第一种和第二种设计方法的效果，第二种设计方法较好。从图9中可以看出，基于三种设计参数的减震效果(绝对加速度)相差不大。

表7表示原结构与基于定点理论设计的消能减震结构位移差值和原结构位移值的比值；表8表示原结构与基于第二种方法设计的消能减震结构位移差值和原结构位移值的比值。表7和表8比较可知，定点理论和第二种设计方法的位移降低率，在结构下部很接近，结构上部相差在20%左右。

基于上述的观察和分析，本文提出如下见解：如果子结构的质量不能满足定点理论所需要的质量，但是大于定点理论所需最大质量的30%时，可以参考本文的第二种设计方法来进行设计。为了便于讨论，下文将第二种设计方法叫做定点理论修正法。

图8 最大位移Fig.8 Maximum displacement

图9 最大绝对加速度Fig.9 Maximum absolute acceleration

Tab.7 Reduction rate of maximum displacement %

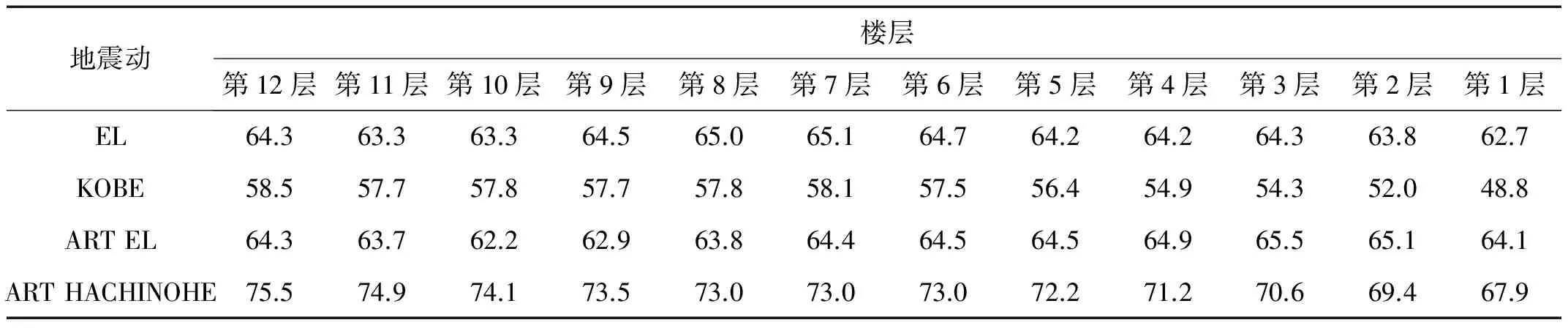
表8 最大位移降低率

4.3 优化分析

为了验证本文提出的定点理论修正法的合理性、优越性以及优化分析，选择如下几种工况，采用EL CENTRO波、 KOBE波、ART ELCENTRO波、ART HACHINOHE波分析其位移和加速度反应。工况0表示原结构；工况1表示只在第3层附加TMD；工况2表示只在第7层附加TMD；工况3表示只在第12层附加TMD；工况4表示第12层、7层、3层附加TMD；工况5表示12层结构每层都附加TMD。

图10表示最大位移，图11表示最大绝对加速度。 由图10可知，工况2、工况3和工况4位移减小比较明显,其中工况4的位移减震效果最好，工况1和工况5的位移减震效果差。由图11可知，工况4的加速度值都要小于工况1，工况2，工况3，工况5的加速度值，由此可见工况4的加速度减震效果最好。

结果证明按照本文提出的定点理论修正法设计的附加子结构的结构，在一定程度上可以引起消能减震的效果。此外，通过上述5种工况的比较可知，若只在一层附加TMD，则TMD所在的楼层越高，减震效果越好；每一层都附加TMD的减震效果不甚理想。

图10 最大位移Fig.10 Maximum displacement

图11 最大绝对加速度Fig.11 Maximum absolute acceleration

5 地震反应分析及能量关系

为了进一步考察本文提出的“定点理论修正法”的可靠性，利用如下篇幅考察位移、加速度反应值以及能量输入、消耗的情况。

5.1 位移反应

图12～图14分别表示原结构第12层、7层、3层与消能结构第12层、7层、3层的位移反应值，横坐标表示时程，纵坐标表示位移反应值。

由图12～图14中可知，在原结构上附加TMD后，地震位移反应都能明显减小。

5.2 加速度反应

图15～图17分别表示原结构第12层、7层、3层与消能结构第12层、7层、3层的加速度反应值。横坐标表示时程，纵坐标表示加速度反应值。

由图15～图17可知，在原结构上附加TMD后，加速度反应都能够得到明显减小，其中第12层减小更明显。

5.3 层间位移角

图18表示在4条地震动作用下，结构的层间位移角，根据《建筑抗震设计规范》的规定，在罕遇地震作用下，结构的层间位移角限值为1/50。横坐标表示层间位移角，纵坐标表示层数。由图18可知，附加TMD后各层的层间位移角都小于原结构的层间位移角，并且大大改善了原结构层间位移不均匀的情况，能够避免损伤集中的问题。

图12 第12层位移反应Fig.12 Displacement response of 12th floor

图14 第3层位移反应Fig.14 Displacement response of 3th floor

图15 第12层加速度反应Fig.15 Absolute acceleration response of 12th floor

图16 第7层加速度反应Fig.16 Absolute acceleration response of 7th floor

图17 第3层加速度反应Fig.17 Absolute acceleration response of 3th floor

图18 最大层间位移角Fig.18 Tnterstory drift ratio

5.4 滞回曲线

图19表示4条地震动作用下第12层的TMD滞回曲线，横坐标表示位移，纵坐标表示剪力。

由图19可以看出，在4种地震动作用下TMD都进入塑性状态，消耗了一定的能量，从而减小了主结构自身消耗的能量，达到保护主结构的目的。

5.5 能量关系

图20表示附加TMD后的地震动输入于结构的总能量和结构消耗的总能量。可知，在4条不同的地震动作用下，输入的能量与消耗的能量是相等的，即满足能量守恒。如果自编电算程序有错，则得不到“能量守恒”的结果，故这一结果也能证明了自编电算程序的可靠性。

图21表示4条地震动作用下主结构的阻尼能。附加TMD后主结构自身阻尼耗能明显减小，提高了结构的抗震性能。

图22表示4条地震动作用下主结构耗能(EZ)、TMD耗能(ET)、总耗能(EH)占地震输入能量(E)的比例。由图22可知，地震动作用初始阶段，主结构耗能比较大，TMD耗能比较小，随着地震动作用时间的增加，主结构耗能逐渐减小而TMD耗能逐渐增大。在地震动作用初始阶段，TMD 还没充分发挥作用，主要靠主结构耗能，随着作用时间的增大，TMD逐步发挥作用消耗了大部分能量，最后趋于稳定，稳定后主结构消耗地震输入能量的15%，而TMD消耗了85%，且主结构与TMD的耗能总和与地震动带来的能量一致。充分说明结构附加TMD后，TMD能消耗地震带来的大部分能量，减小了主体结构的耗能，从而很好的保护了主结构，起到很好的减震效果。

图19 TMD滞回曲线Fig.19 The Hysteretic curve of TMD

图20 消能减震结构总耗能与地震输入能量的比较Fig.20 Comparison of total energy consumption and seismic input energy

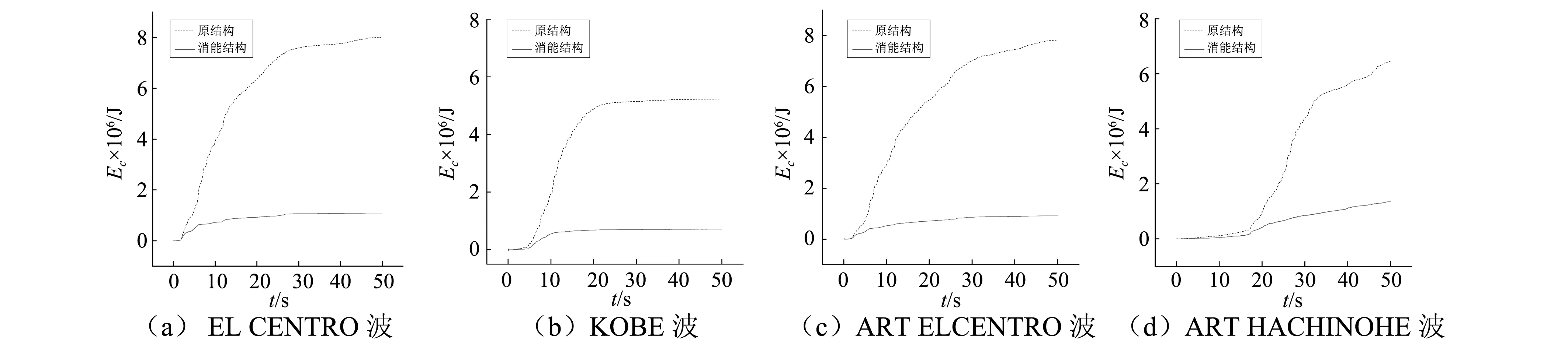
图21 阻尼能Fig.21 Damping energy

图22 各部分耗能占地震输入能量的比例Fig.22 Each part of the energy consumption accounts for the seismic input energy

6 TMD的设计方法

通过计算分析可知本文提出的新型子结构形态是可行且可靠的。由12层钢框架结构的算例分析对定点理论修正法的合理性和可靠性进行了验证，结果表明该方法可行且对工程实例设计具有一定的参考意义。

(1)设定设置子结构的楼层。

通过结构振型分析，绘制前几阶振型向量，确定前几阶振型最大振幅出现的楼层，设定设置子结构的楼层。

(2)计算子结构参数。

利用式(3)～式(5)、式(9)，计算与前几阶振型相对应的等效质量、刚度、质量比和目标阻尼比；利用式(6)～式(8)，计算与前几阶阵型相对应的子结构的质量、抗侧刚度和阻尼系数。

(3)选择计算方法。

如果利用式(6)计算的与前几阶阵型相对应的子结构的质量大于等于由带肋楼板的恒载和活荷载换算为子结构的质量，则采用定点理论来进行设计，若小于则由带肋楼板的恒载和活荷载换算为子结构的质量，采用本文提出的定点理论修正法进行设计。

7 结 论

基于TMD的设计方法对算例模型进行计算分析后可得出如下结论：

(1)通过对附加TMD结构的地震响应、能量关系分析比较可知，在结构上附加该TMD形成的消能减震结构具有良好的减震控制效果。

(2)根据算例模型的结构振型，研究了子结构的设置位置及个数对消能结构地震响应的影响。通过分析可知，将所有振型选作减震对象来设置子结构的减震效果并不理想，而选择影响较大的前三阶振型作为减震对象设置子结构时的减震效果好。

(3)算例模型附加该TMD后结构的位移响应，加速度响应，层间位移角都有非常显著的减小。TMD充分发挥作用，消耗了地震输入能量的80%～85%，大大降低了主体结构的自身耗能，使结构完全处于弹性状态，不发生塑性变形，从而很好的保护了主体结构。

[ 1 ] 陈永祁,彭程,马良喆.调谐质量阻尼器(TMD)在高层结构上 应用的总结与研究[J].建筑结构，2013(增刊2):269-275. CHEN Yongqi , PENG Cheng , MA Liangzhe. Effect analysis of tuned mass damper ( TMD) in high-rise structure[J]. Building Structure， 2013(Sup 2):269-275.

[ 2 ] 徐家云,雷静雅.小高层建筑中屋顶花园TMD的振动控制作用[J].自然灾害学报,2005,14(4) :154-157. XU Jiayun，LEI Jingya. Vibration control effect of roof garden as a TMD in mid-rise building[J].Journal of Natural Disaster, 2005,14(4):154-157.

[ 3 ] 王磊,谭平,方创杰，等. 屋顶水箱TMD对加固结构的减震控制研究[J].四川建筑科学研究,2013,39(3):166-169.

WANG Lei, TAN Ping, FANG Chuangjie, et al. Application of roof tank TMD in structural reinforcement design[J].Sichuan Building Science,2013,39(3):166-169.

[ 4 ] 田志昌,钱稼茹.作为动力消振器的滑动屋盖系统[J].工程力学,2002,19(1):29-33. TIAN Zhichang, QIAN Jiaru. Sliding roof system-a vibration absorber for buildings[J].Engineering Mechanics,2002,19(1):29-33.

[ 5 ] 翁大根,蒋通,施卫星，等.楼面滑动隔震装置设计与试验研究[J].世界地震工程,2001,17(3):109-115. WENG Dagen, JIANG Tong, SHI Weixing, et al. Study on the floor sliding isolation system[J].World Information Earthquake Engineering,2001,17(3):109-115.

[ 6 ] 冼巧玲,刘建安,周福霖.楼板隔震消能结构的振动台试验研究[J].地震工程与工程振动,2008,28(3):145-151. XIAN Qiaoling, LIU Jian’an, ZHOU Fulin. Shaking table test on the slab isolating and energy dissipating (SIED) structure [J].Journal of Earthquake Engineering and Earthquake Vibration,2008,28(3):145-151.

[ 7 ] 韦长庚. 室内设施隔震-房屋结构减震体系的初步研究[D].广州：广州大学,2013.

[ 8 ] 中华人民共和国住房和城乡建设部.建筑结构荷载规范: GB 50009—2012 [S].北京：中国建筑工业出版社，2012.

[ 9 ] 建筑隔震橡胶支座主要力学性能[Z].西安达盛隔震技术有限公司.

[10] 背户一登.结构振动控制[M].北京：机械工业出版社,2010.

[11] 张敏.建筑结构抗震分析与减震控制[M].成都：西南交通大学出版社,2007:189-197.

[12] 裴星洙.建筑结构抗震分析与设计[M].北京：北京大学出版社,2013:126-138.

A design method of TMD with ribbed floor as the mass

PEI Xingzhu1， SUN Jianjie2

(1. School of Civil Engineering and Architecture, Jiangsu University of Science and Technology，Zhenjiang 212003, China；2. Shanghai MCC20 Construction Co.，Ltd.，Shanghai 201999,China)

In order not to increase the weight of a structure, and make the TMD principle well applied to the structural seismic response control of tall buildings, this paper presents a TMD system. In the system, dead loads and live loads of ribbed floor were converted into the quality of substructure and lateral stiffness and damping of a rubber isolation pad set in the main beam (including beam) and ribbed slab replaced the spring and damper of the substructure. Based on the study of rise building with TMD, vibration differential equations and computer programs were established for elastic-plastic time history analysis and the rationality and feasibility of the system was discussed. A design method of TMD was studied based on the fixed point theory. The seismic responses of original structure and energy dissipation structure were calculated under a variety of earthquake actions and the energy distribution was compared. The effect of the TMD location on energy dissipation structure seismic response? was considered and the feasibility and scheme of the TMD used in practical engineering was analyzed. Finally a simple and effective design method of TMD was presented, the theory of fixed point correction method. Based on the method, case models were used for simulations. It is proved that structure has better effect of energy dissipation based on this method and the theory of fixed point correction method is reasonable and reliable.

tuned mass damper; design method; seismic response; energy relations

2016-03-03 修改稿收到日期： 2016-06-20

裴星洙 男，博士，教授，1954年生

TU352

A

10.13465/j.cnki.jvs.2017.16.026