基于格林理论的鬼波压制方法及其应用

杨金龙,Weglein Arthur B

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京 211103;2.The University of Houston,Houston 77004,USA)

基于格林理论的鬼波压制方法及其应用

杨金龙1,Weglein Arthur B2

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京 211103;2.The University of Houston,Houston 77004,USA)

海洋地震资料存在受海水面虚反射(鬼波)引起的陷波效应,为此,从散射理论出发,提出了基于格林理论的空间-频率(x-ω)域任意震源鬼波压制方法,并详细论述了其物理意义。在一维理论数据分析的基础上,形成了格林理论鬼波压制处理流程。利用模拟数据和实际数据进行了测试,实现了基于上下缆和双检采集地震资料的鬼波压制。处理结果表明,此方法完全基于地震数据驱动,无需任何地下介质信息,适用于各种复杂的海洋地形和地质情况。鬼波压制后地震资料的频带得到有效拓宽、地震资料的分辨率得到提高,有利于地震资料的后续处理和解释。

虚反射;陷波效应;鬼波压制;散射理论;格林理论

在海洋地震勘探中,电缆和气枪都以一定深度沉放在海平面以下,以加强下传的激发能量和降低接收环境噪声。由于海平面是强反射界面,在激发和接收环节都会产生虚反射(又称鬼波),从而压制了地震反射信号的低频和高频能量,并产生了陷波点,降低了原始地震资料的频带宽度和分辨率[1-4]。要获得宽频带的地震剖面,必须在地震资料采集或处理阶段尽量消除鬼波的影响。目前高精度、高分辨率地震处理解释都需要丰富的低、高频信息,因此鬼波压制、拓宽频带是海洋地震勘探中的重点研究课题之一。

另一方面,随着海上地震勘探进入深水领域,特别是面向深层和超深层地质目标的勘探,需要解决深层地震反射能量弱、信噪比低的问题[5]。而低频信号穿透能力强,为了获得深层弱有效信号,通常采用低频能量强的枪阵组合并加大电缆沉放深度的采集方式[6]。但受海水面的鬼波干涉影响,电缆接收的地震信号存在严重的陷波作用,而且电缆沉放深度越深高频信号受到的压制越大,从而导致地震资料频带变窄,其分辨率和信噪比降低,特别是持续的鬼波同相轴也给地震地质解释造成困难[7-9]。鬼波压制可以有效提升低频端信号能量,因此,它也是解决海域深层勘探问题的关键之一。

在海洋地震资料处理中,为了消除虚反射(压制鬼波)、拓宽频带、提高信号分辨率,HILL等[10]、MOLDOVEANU等[6]提出了上下缆采集技术;刘春成等[9]、GU等[11]优化了上下缆沉放深度组合;OZDEMIR等[12]利用最小二乘法优化了上下缆采集的去鬼波算子;赫建伟等[13]利用频率波数谱分析了上下缆数据的陷波特征,提出了一种噪声自适应上下缆数据合并技术;管西竹等[14]推导了基于波动方程的鬼波波场和有效波场的延拓方法,有效地解决了上下缆中的鬼波和有效波的干涉问题;赵仁永等[15]研究了上下源、上下缆采集与处理技术在珠江口的应用,并取得了较好的效果。但是,上下缆采集技术要求上下缆在同一垂直剖面内,对电缆的定位精度要求很高,而且利用两条电缆进行采集的成本比较高。为此,TENGHAMN等[16]、CARLSON等[17]和DAY等[18]提出了双传感器(压力和速度传感器)地震拖缆采集技术(GeoStreamer),利用它们的上行波和下行波极性特点来压制鬼波,拓宽频带,该技术对双检拖缆性能要求很高,鬼波压制的效果受到压力和速度传感器各自不同灵敏度的影响。近年来,SOUBARAS等[19]提出了变深度拖缆(斜缆)采集技术;SOUBARAS[20-21]和SABLON等[22]利用斜缆陷波多样性,通过常规偏移和镜像偏移联合反褶积技术压制鬼波,在墨西哥湾等地的试验结果证明了该方法能有效地拓宽频带;许自强等[23]提出了最优化联合反褶积鬼波压制算法。各大地球物理公司也推出了各自的宽频地震采集与处理技术,并取得了较好的应用效果。对于常规拖缆采集,LINDSEY[24]提出了线性滤波法压制鬼波方法;JOVANOVICH等[25]提出了利用反褶积方法压制鬼波,但是去鬼波算子存在一系列“零值点”,导致算法不稳定;WEGLEIN等[26]提出了运用逆散射级数法(ISS)压制鬼波和多次波;王芳芳等[27]讨论了应用ISS法压制鬼波遇到的实际问题,并进行改进。

上述鬼波压制方法都是在波数-频率(k-ω)域进行压制,WEGLEIN等[4]从散射理论出发,提出了利用格林理论在x-ω域中压制鬼波的思想;ZHANG[28-29]发展了格林理论鬼波压制算法,并成功应用于海洋地震数据;MAYHAN等[30]改进了该算法,并在墨西哥湾实际数据处理中取得了较好的效果;WU等[31]进一步将格林理论鬼波压制算法扩展到陆上地震数据。YANG[32]证明了鬼波的存在对压制自由表面和层间多次波的影响;TANG等[33]阐述了鬼波压制在后续地震资料处理中的重要性。WEGLEIN等[34]还研究了格林理论在波场分离(直达波和反射波分离)和子波提取中的应用。国内,基于格林理论的鬼波压制方法仍处于探索阶段,李洪建等[35]初步推导了格林理论鬼波压制算法的数学公式,并利用模拟和实际数据进行了验证,但忽略了该方法的物理意义及其具体应用过程。本文从散射理论出发,根据波场传播的物理意义提出了在x-ω域进行格林理论鬼波压制的原理,并通过一维理论数据分析,形成了格林理论鬼波压制具体处理流程。模拟和实际数据处理结果表明此方法纯数据驱动,无需任何地下介质信息,适用于各种复杂的海洋地形和地质情况,可以有效地压制鬼波、拓宽频带。在实际数据鬼波压制过程中,本文采用了抛物Radon变换法进行近道插值。

1 方法原理

基于格林理论的鬼波压制方法是从散射理论[36](或称扰动理论)和格林理论推导而得。在散射理论中,实际介质由2部分组成:参考介质(或称参考背景)和扰动介质。相应地,实际波场也由2部分组成:参考波场和扰动波场。在参考介质中传播的波场称为参考波场;在实际介质中传播的波场称为实际波场;扰动波场为实际波场和参考波场的差。参考介质可以自由选取,可以根据具体问题的需要和解决问题的方便性而选取。在海洋地震勘探中,直达波和反射波的分离可选取空气和海水作为参考介质;鬼波压制可选取全空间海水介质作为参考介质(如图1)。在鬼波压制中,实际介质由参考介质(海水介质)和两部分扰动介质(地层结构对海水的扰动αearth和空气对海水的扰动αair)组成。频率域压力波场P满足任意震源ρ1的非均匀介质Helmholtz方程:

图1 格林理论鬼波压制原理(V为选取的体积,S为体积V的表面积)

(1)

(2)

式中:c0为声波在参考介质中的传播速度。则非均匀介质的Helmholtz方程变为:

(3)

即相当于有3个震源的均匀介质Helmholtz方程。此处,ρ1为主动震源,ρ2和ρ3为次生震源,分别由地层结构和空气对海水介质的扰动产生。已知,一个脉冲震源(δ)的均匀介质Helmholtz方程为:

(4)

它的解是格林函数G0(r,r′,ω)。利用格林函数式可以求出公式的解:

(5)

式中:r′为积分变量,即对所有空间积分。根据公式的右边部分可知,在检波器端,接收到的压力波场P可简化为3部分组成(如图2),分别为来自3个震源的波场,震源ρ1的直达波(第一项)、震源ρ2的海面反射下行波(第二项),即鬼波,震源ρ3的海底反射上行波(第三项)。海洋数据处理一般是先去除直达波然后压制鬼波,即先切除来自震源ρ1的直达波,然后压制来自震源ρ2的海面反射下行波,最终得到来自震源ρ3的海底反射上行波。

格林理论(或格林第二恒等式)为:

图2 检波器接收来自3个震源的波场的示意

(6)

(7)

如果选取的预测检波点波场位置r在体积V内海平面以下、检波点测量面以上,则∫VP(r′,rs,ω)δ(r-r′)]dr′=P(r,rs,ω)。公式(7)左边第二项与第四项相互抵消,且在体积V内ρ3≡0,αearth≡0,因此,公式(7)变为:

(8)

在体积V内,公式(8)左侧为总波场减去来自震源ρ1的直达波和来自震源ρ2的海面反射下行波。在体积V内对比公式(5)和公式(8),并引入Sommerfeld辐射条件,对整个闭合表面S的积分可以表示成对测量面(measurement surface,m.s.)的积分,鬼波压制后的上行波场为:

(9)

(10)

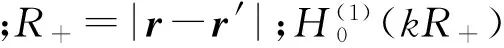
基于(9)式格林理论鬼波压制方法的优点如下:①在x-ω域进行处理,无需转换到k-ω域,适用于任意采集曲面;②适用于单炮数据,因此占用内存小,计算速度快;③只需地震数据P和地震数据垂向导数∂/∂z′P,无需预知地下介质信息,因此是完全数据驱动的鬼波压制方法,适用于各种复杂的海洋地形和地质情形;④该方法不局限于点震源的情况,适用于任意气枪组合震源;⑤对地震数据中直达波的处理没有要求,切除或保留直达波,本文方法都适用;⑥一般鬼波压制方法都是先预测后相减,但是由于有效信号与鬼波相互叠加干扰,相减非常困难,而本文方法是直接得到鬼波压制后的结果,避免了先预测后相减的难题。

对于双检地震采集,通过压力检波器和速度检波器可以测得压力波场地震数据P和垂直速度波场Vz,并通过对应关系∂/∂zP=iωρVz获得地震数据垂向导数,其中ρ为参考介质密度。对于上下缆地震采集,地震数据垂向导数可通过∂/∂zP=(P2-P1)/(z2-z1)获得,式中P1和P2为在深度z1和z2的上下缆压力波场。此外,格林理论鬼波压制方法无需转换到k-ω域进行鬼波压制,而在k-ω域的P-Vz鬼波压制方法[3,38]只是格林理论鬼波压制方法的一个推论[30],需要假设测量面为水平面,通过对检波点做傅里叶变换得到。在k-ω域的P-Vz方法一般是现代地震勘探鬼波压制的工业标准方法,因此,格林理论鬼波压制方法是一个更普遍的方法。

在单炮点地震数据中,格林理论鬼波压制方法(公式(9))压制了检波点鬼波,震源鬼波的压制从炮检互换理论出发,先对炮点插值到与检波器间距相同,并交换炮检位置,数据从炮点道集转换到检波点道集,此时震源鬼波变成检波点鬼波,再次运用格林理论鬼波压制法,可相应地压制震源鬼波[28]。

2 理论分析

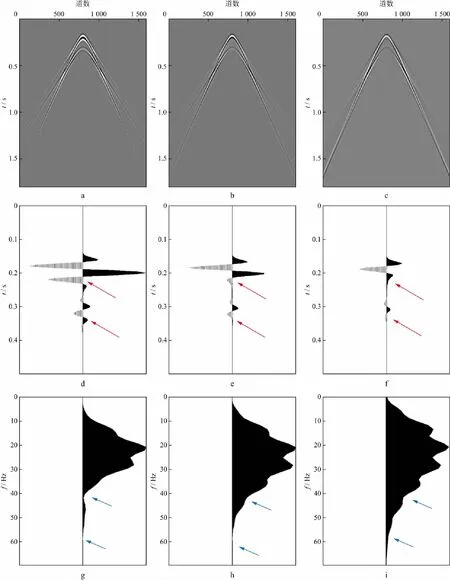
首先我们通过一维理论分析来验证格林理论鬼波压制方法的有效性,并阐述鬼波压制过程中波场分离的物理意义和鬼波压制的具体处理流程。对于一维(1D)垂直入射情况,假设0

图3 一维理论实验示意

图4 一维理论数据包含信号示意

下面利用此数据来验证格林理论鬼波压制方法。

在x-ω域,地震数据可表示为:

(11)

其中,海平面的反射系数为-1,海底反射系数为R。在全空间海水参考介质中的一维格林函数为公式(10)的第一种情况:

(12)

假设使用双检或上下缆采集,地震数据的垂向导数已测得,即地震数据公式(11)的导数:

(13)

将(12)式和(13)式代入到一维格林理论鬼波压制算法((9)式)中,可得:

(14)

式中:z为预测点深度,在海平面与检波器之间0

(15)

已知zg>z,所以sgn(zg-z)=1,公式(14)可简化为:

(16)

所得结果即为海底反射一次波(上行波),即无鬼波的地震数据。换句话说,格林理论鬼波压制方法非常有效地压制了检波器鬼波,而且还可以压制由主动震源产生的直达波以及直达波鬼波,并保留了原数据中的上行波。通过一维理论数据分析,验证了格林理论鬼波压制算法的有效性。

3 实例分析

前面详细论证了格林理论鬼波压制的方法原理及其物理意义,并通过一维理论分析论证了该方法的有效性以及阐述了该方法鬼波压制的具体处理流程,下面利用模拟数据和实际数据对该方法进行验证。

3.1 模拟数据应用

利用简单层状模型模拟数据对本文方法进行验证和分析。简单层状模型有2层(如图5),水深90m,海水层速度为1500m/s,海水层以下速度为2250m/s,震源深度13m,检波器深度18m,共1601道,道间距3m,震源采用主频25Hz的雷克子波,采样间隔0.004s,记录时间为1.8s。根据陷波频率公式可知:

(17)

图5 模拟数据模型示意

图6b和图6c分别为压制检波点鬼波和震源鬼波后的结果。为了突出更多细节,从图6a到图6c中选取中间道(见图6d到图6f)来分析,可以看出在红色箭头处,一次波和表面多次波的震源鬼波和检波器鬼波都得到了有效压制,并且保证了一次波和表面多次波信号不受损伤。频谱分析(图6g到图6i)可知,鬼波压制后,陷波点(蓝色箭头处)得以消除,低频成分得到有效补偿,频谱更连续,频带得到了拓宽。由此可见,格林理论鬼波压制方法可以有效压制虚反射(鬼波),弥补由于鬼波存在而导致的频谱缺失。

图6 模拟数据压制鬼波前后以及频谱分析a 产生的模拟数据; b 压制检波点鬼波后的结果; c 压制震源鬼波后的结果; d 从图6a中选取的中间道; e 从图6b中选取的中间道; f 从图6c中选取的中间道; g 图6a的频谱; h 图6b的频谱; i 图6c的频谱

3.2 实际数据应用

实际数据需要经过预处理后再进行鬼波压制,因此,我们设计了格林理论鬼波压制方法的处理流程,具体如下:

1) 原始数据预处理,低频滤波、涌浪噪声压制和去气泡;

2) 高分辨率抛物Radon变换法波场外推,恢复近偏移距波场;

3) 求取波场垂向导数,进行格林理论鬼波压制。

在实际数据处理中,恢复近偏移距数据非常重要,而在模拟数据中则不需要，这是因为模拟数据是从零偏移距开始模拟,而实际数据由于采集条件的限制,只能从某一偏移距开始采集。利用抛物Radon变换法进行波场外推,首先将波场转换到频率-慢度域,然后进行波场外推,最后将处理后的波场反变换回空间-频率域再进行鬼波压制。此处,我们选取海上双检地震数据进行鬼波压制处理和分析,数据包括海上水检和陆检记录,震源深度为9m,检波器深度25m,采样间隔0.004s,记录长度14.34s,每炮960道,道间距12.5m,最小偏移距112m。水检测得压力波场,陆检测得垂向速度分量,可通过对应关系∂P/∂z=iωρVz,获得波场垂向导数。经过数据预处理和近道恢复后,获取图7a所示的鬼波压制前实际数据(选取3.0～4.0s),利用格林理论鬼波压制方法压制检波器鬼波(图7b),进一步通过炮检互换,压制震源鬼波(图7c)。鬼波压制后,由于鬼波产生的虚假同相轴被有效去除,地震记录分辨率得到明显提高。任意抽取数据鬼波压制前后(图7a到图7c)中一道(第5道)进行对比分析,鬼波压制后波形逐渐恢复到子波波形。说明即使有效波与其相应的鬼波重合或相干时,格林理论鬼波压制方法也可以有效地压制鬼波,并确保有效信号不被损伤。

图7 利用格林理论鬼波压制方法压制实际数据鬼波前后对比及任意抽取的一道数据分析a 鬼波压制前实际数据(选取3.0～4.0s); b 检波器鬼波压制后数据; c 震源鬼波压制后数据; d 从图7a中任意抽取的一道数据; e 从图7b中任意抽取的一道数据; f 从图7c中任意抽取的一道数据

图8对比了地震数据检波器鬼波压制前后的频谱,从中可以看出,检波器鬼波陷波点(蓝色线)大约在30,60和90Hz,鬼波压制后(红色线),陷波点得以消除,能量得到有效提升,频谱更连续,频带得到了拓宽。因此,通过实际数据处理可以看出,格林理论鬼波压制方法可以有效地压制鬼波,弥补由于鬼波存在引起的频谱缺失,提高了地震数据的分辨率。

图8 实际数据鬼波压制前(蓝色)、后(红色)频谱分析

4 结论

本文从散射理论出发,提出了基于格林理论的x-ω域鬼波压制方法,并详细论述了其物理意义。

通过理论分析,验证了本文方法的有效性并形成了鬼波压制的具体处理流程。模拟数据和实际数据测试,实现了基于上下缆和双检采集地震资料的鬼波压制。模拟数据的处理表明,该方法可以有效地压制鬼波,消除由于鬼波存在引起的陷波点,弥补了频谱缺失,拓宽了地震资料的频带,提高了地震资料的分辨率,并确保有效信号不被损伤。应用于实际地震资料处理时,需要先对资料进行预处理和近偏移距恢复，然后才能进行鬼波压制,鬼波压制后可以消除陷波效应,提升地震资料能量,有利于地震资料的后续处理和解释。本方法避免了常规地震采集中鬼波压制去鬼波算子不稳定的问题,适用于已存在的海域宽频地震采集方法,如双检和上下缆采集,在海洋地震勘探,尤其是面向深层和超深层地质目标的勘探中有广阔的应用前景。

致谢:感谢休斯敦大学Jim Mayhan博士在实际地震数据处理中的帮助。

[1] HAMARBITAN N S,MARGRAVE G F.Spectral analysis of a ghost[J].Geophysics,2001,66(4):1267-1273

[2] CORRIGAN D,WEGLEIN A B,THOMPSON D D.Method and apparatus for seismic survey including using vertical gradient estimation to separate downgoing seismic wavefields:US 55051961 [P].1991-09-24

[3] AMUNDSEN L.Wavenumber-based filtering of marine point-source data[J].Geophysics,1993,58(9):1335-1348

[4] WEGLEIN A B,SHAW S A,MATSON K H,et al.New approaches to deghosting towed-streamer and ocean-bottom pressure measurements[J].Expanded Abstracts of 72ndAnnual Internet SEG Mtg,2002:1016-1019

[5] 陈金海,王桂华,徐新南.海上地震虚反射探讨[J].海洋石油,2000,20(1):22-27 CHEN J H,WANG G H,XU X N.Assessment of ghosts in marine seismic data[J].Offshore Oil,2000,20(1):22-27

[6] MOLDOVEANU N,COMBEE L,EGAN M,et al.Over/under towed-streamer acquisition:a method to extend seismic bandwidth to both higher and lower frequencies[J].The Leading Edge,2007,26(1):41-58

[7] KROODE F,BERGLER S,CORSTEN C,et al.Broadband seismic data—the importance of low frequencies[J].Geophysics,2013,78(2):WA3-WA14

[8] 余本善,孙乃达.海上宽频地震采集技术新进展[J].石油科技论坛,2015,34(1):41-45 YU B S,SUN N D.Latest development of marine broadband seismic acquisition technology[J].Oil Forum,2015,34(1):41-45

[9] 刘春成,刘志斌,顾汉明.利用上/下缆合并算子确定海上上/下缆采集的最优沉放深度组合[J].石油物探,2013,52(6):623-629 LIU C C,LIU Z B,GU H M.The determination of optimal sinking depths of over/under streamers in offshore survey by merge operator[J].Geophysical Prospecting for Petroleum,2013,52(6):623-629

[10] HILL D,COMBED L,BACON J.Over/under acquisition and data processing:the next quantum leap in seismic technology[J].First Break,2006,24(6):81-95

[11] GU H M,CHENG J W,CAI C G,et al.Optimal towing depth for over/under streamer acquisition from deghosting operator analysis[J].Expanded Abstracts of 83thAnnual Internet SEG Mtg,2013,148-152

[12] OZDEMIR A K,CAPRIOLI P,OZBEK A,et al.Optimized deghosting of over/under towed-streamer data in the presence of noise[J].The Leading Edge,2008,27(2):190-199

[13] 赫建伟,陆文凯,李忠晓.一种自适应上下缆地震数据合并技术[J].应用地球物理,2013,10(4):469-476 HE J W,LU W K,LI Z X.An adaptive over/under data combination method[J].Applied Geophysics,2013,10(4):469-476

[14] 管西竹,陈宝书,符力耘,等.基于波动方程的上下缆地震数据鬼波压制方法研究[J].地球物理学报,2015,58(10):3746-3757 GUAN X Z,CHEN B S,FU L Y,et al.The study of a deghosting method of over/under streamer seismic data based on wave equation[J].Chinese Journal of Geophysics,2015,58(10):3746-3757

[15] 赵仁永,张振波,轩义华.上下源、上下缆地震采集技术在珠江口的应用[J].石油地球物理勘探,2011,46(4):517-521 ZHAO R Y,ZHANG Z B,XUAN Y H.Application of over/under sources and over/under streamers acquisition in Pearl River Mouth Basin[J].Oil Geophysical Prospecting,2011,46(4):517-521

[16] TENGHAMN R,VAAGE S,BORRESEN C.A dual-sensor towed marine streamer:its viable implementation and initial results[J].Expanded Abstracts of 77thAnnual Internet SEG Mtg,2007:989-992

[17] CARLSON D,LONG A,SOLLNER W,et al.Increased resolution and penetration from a towed dual-sensor streamer[J].First Break,2007,25(12):71-77

[18] DAY A,KLUVER T,SOLLNER W,et al.Wavefield separation methods for dual-sensor towed-streamer data[J].Geophysics,2013,78(2):WA55-WA70

[19] SOUBARAS R,DOWLE R.Variable-depth streamer—a broadband marine solution[J].First Break,2010,28(12):89-96

[20] SOUBARAS R.Deghosting by joint deconvolution of a migration and a mirror migration[J].Expanded Abstracts of 80thAnnual Internet SEG Mtg,2010:3406-3410

[21] SOUBARAS R.Pre-stack deghosting for variable-depth streamer data[J].Expanded Abstracts of 82ndAnnual Internet SEG Mtg,2012:785-789

[22] SABLON R,RUSSIER D,ZURITA O,et al.Multiple attenuation for variable-depth streamer data:from deep to shallow water[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011:3505-3509

[23] 许自强,方中于,顾汉明,等.海上变深度缆数据最优化压制鬼波方法及其应用[J].石油物探,2015,54(4):404-413 XU Z Q,FANG Z Y,GU H M,et al.The application of optimal deghosting algorithm on marine variable-depth streamer data[J].Geophysical Prospecting for Petroleum,2015,54(4):404-413

[24] LINDSEY J P.Elimination of seismic ghost reflections by means of a linear filter[J].Geophysics,1960,25(1):130-140

[25] JOVANOVICH D B,SUMNER R D,AKINS-EASTERLIN S L.Ghosting and marine signature deconvolution:a prerequisite for detailed seismic interpretation[J].Geophysics,1983,48(11):1468-1485

[26] WEGLEIN A B,GASPAROTTO F A,CARVALHO P M,et al.An inverse scattering series method for attenuating multiples in seismic reflection data[J].Geophysics,1997,62(6):1975-1989

[27] 王芳芳,李景叶,陈小宏.基于逆散射级数法的鬼波压制方法[J].地球物理学报,2013,56(5):1628-1636 WANG F F,LI J Y,CHEN X H.Deghosting method based on inverse scattering series[J].Chinese Journal of Geophysics,2013,56(5):1628-1636

[28] ZHANG J F.Wave theory based data preparation for inverse scattering multiple remvoal,depth imaging and parameter estimation:analysis and numerical tests of Green’s theorem deghosting theory[D].Houston:The University of Houston,2007

[29] ZHANG J F,WEGLEIN A B.Application of extinction theorem deghosting method on ocean bottom data[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006:2674-2678

[30] MAYHAN J D,WEGLEIN A B.First application of Green’s theorem-derived source and receiver deghosting on deep-water Gulf of Mexico synthetic (SEAM) and field data[J].Geophysics,2013,78(2):WA77-WA89

[31] WU J,WEGLEIN A B.Elastic Green’s theorem preprocessing for on-shore internal multiple attenuation:Theory and initial synthetic data tests[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014:4299-4304

[32] YANG J L.Extending the inverse scattering series free-surface multiple elimination and internal multiple attenuation algorithms by incorporating the source wavelet and radiation pattern:Examining and evaluating the benefit and added-value[D].Houston:The University of Houston,2014

[33] TANG L,MAYHAN J D,YANG J L,et al.Using Green’s theorem to satisfy data requirements of inverse scattering series multiple removal methods[J].Expanded Abstracts of 83rdAnnual Internat SEG Mtg,2013:4392-4396

[34] WEGLEIN A B,SECREST B G.Wavelet estimation for a multidimensional acoustic earth model[J].Geophysics,1990,55(7):902-913

[35] 李洪建,韩立国,巩向博,等.基于格林函数理论的波场预测和鬼波压制方法[J].地球物理学报,2016,59(3):1113-1124LI H J,HAN L G,GONG X B,et al.A wavefield prediction and ghost suppression method based on Green function theory[J].Chinese Journal of Geophysics,2016,59(3):1113-1124

[36] WEGLEIN A B,ARAUJO F V,CARVALHO P M,et al.Inverse scattering series and seismic exploration[J].Inverse Problem,2003,19(6):R27-R83

[37] MORSE P M,FESHBACH H.Methods of theoretical physics[M].New York:McGraw-Hill Book Company,1953:1-997

[38] ROBERTSSON J O A,KRAGH E.Rough-sea deghosting using a single streamer and a pressure gradient approximation[J].Geophysics,2002,67(6):2005-2011

[39] DE HOOP A T,VAN DER HIJDEN J H M T.Generation of acoustic waves by an impulsive line source in a fluid/solid configuration with a plane boundary[J].Journal of the Acoustical Society of America,1983,74(1):333-342

[40] AKI K,RICHARDS P G.Quantitantive seismology[M].Sausalito:University Science Books,2002:1-700

(编辑：朱文杰)

A deghosting method based on Green’s theorem and its application

YANG Jinlong1,Weglein Arthur B2

(1.SINOPECGeophysicalResearchInstitute,Nanjing211103,China;2.TheUniversityofHouston,Houston77004,USA)

In marine seismic exploration,due to the presence of the air/water surface,the virtual reflection called ghost will produce notches in seismic data.Hence,from the scattering theory,a deghosting method based on Green’s theorem is proposed inx-ωdomain and its physical and mathematical foundation is discussed in detail.The procedure of the deghosting method based on Green’s theorem in space-frequency domain is obtained from the 1D theoretical data analysis.This method is applied to the deghosting tests for the numerical and field seismic data that acquired by the over/under cable and dual-sensor cable.Testing results present that this method is totally data-driven and does not require any subsurface information.It is suitable for any complex and complicated marine topography and geological cases.The results after deghosting show that this method can broaden the bandwidth of the seismic data and enhance the resolution of seismic data,which benefits the later seismic processing and interpretation.

ghost reflection,notches,deghosting,scattering theory,Green’s theorem

2016-07-01;改回日期：2016-10-16。

杨金龙(1981-),男,高级工程师,博士,主要从事地震资料处理中的鬼波、表面多次波和层间多次波压制等研究工作。

国家科技重大专项(2016ZX05014-001-002)资助。

P631

A

1000-1441(2017)04-0507-09

10.3969/j.issn.1000-1441.2017.04.006

This research is financially supported by the Science and Technology Major Project of China (Grant No.2016ZX05014-001-002).