Stochastic responses of tumor immune system with periodic treatment∗
Dong-Xi Li(李东喜)and Ying Li(李颖)
1 College of Data Science,Taiyuan University of Technology,Taiyuan 030024,China
2 College of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China
Stochastic responses of tumor immune system with periodic treatment∗
Dong-Xi Li(李东喜)1,†and Ying Li(李颖)2
1 College of Data Science,Taiyuan University of Technology,Taiyuan 030024,China
2 College of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China
We investigate the stochastic responses of a tumor–immune system competition model with environmental noise and periodic treatment.Firstly,a mathematical model describing the interaction between tumor cells and immune system under external fluctuations and periodic treatment is established based on the stochastic differential equation.Then,sufficient conditions for extinction and persistence of the tumor cells are derived by constructing Lyapunov functions and Ito’s formula.Finally,numerical simulations are introduced to illustrate and verify the results.The results of this work provide the theoretical basis for designing more effective and precise therapeutic strategies to eliminate cancer cells,especially for combining the immunotherapy and the traditional tools.
stochastic responses,environmental noise,tumor–immune system,extinction
1.Introduction
Cancer is becoming the leading cause of death around the world.Traditional cancer treatments include surgery,radiation therapy,and chemotherapy.Cancer immunotherapy has recently gained exciting progress.Studies of tumor and immune system have largely been inspired by the works in Refs.[1] and[2],the authors showed that the immune system can recognize and eliminate malignant tumors.So immunotherapy, such as the cellular immunotherapy,[3]has been studied by researchers.And a number of tumor–immune system competition models have been proposed,such as Kuznetsov–Taylor model[4]and Kirschner–Panetta model.[5]In fact,tumor mi-croenvironment is inevitably affected by environmental noise in realism.Nowadays,noise dynamics have been widely studied in different fields such as metapopulation system[6]and Van der Pol oscillator.[7]In the last years,researchers have studied stochastic growth models of cancer cells,[8–11]using the Lyapunov exponent method and the Fokker–Planck equation method to investigate the stability of the stochastic model. Moreover,from a biological or a clinical point of view,investigations including treatments such as periodic ones are important for a successful treatment,e.g.,Thibodeaux and Schlittenhard[12]investigated the effect of a periodic treatment in the within-hostdynamics of malaria infection and suggested that synchronization with the intrinsic oscillation of infected erythrocytes takes place,leading to an optimal treatment.Sotolongo et al.[13]investigated the effect of immunotherapy under periodic treatment on a deterministic model of tumor– immune system and considered the possibility of suppression of tumor growth.Ideta et al.[14]considered the intermittent hormonal therapy in a model of prostate cancer and they suggested the existence of an optimal protocol to the intermittent therapy.Up to now,the effect of noise and cyclic treatment in the tumor dynamics has been widely studied.And fluctuations induced extinction and stochastic resonance in a model of tumor growth with periodic treatment have been studied.[15]Aisu and Horita[16]numerically investigated the stochastic extinction of tumor cells due to the synchronization effect through a time periodic treatment in a tumor–immune interaction model.
The aim of this paper is to explore the dynamics of a simplified Kuznetsov–Taylor model[17]with both environmental noise and periodic treatment,especially the extinction and persistence.One of the advantages of our study is that we make use of the methods of Itˆo’s stochastic integral and Lyapunov function to derive and analyze the properties of the stochastic tumor–immune system competition model,which is different from the approaches of Fokker–Planck equation and effective potential function used in the existing literature.The other advantage is that the conditions for extinction and strong persistence in the mean of tumor cells are obtained by the strict mathematical proofs.The sufficient conditions for extinction and persistence could provide us a more effective and precise therapeutic schedule to eliminate tumor cells and improve the treatment of cancer.
This paper is organized as follows.In Section 2,thestochastic tumor–immune model with periodic treatment is derived.In Section 3,we establish the sufficient conditions for extinction and strong persistence in the mean of tumor cells. Numerical simulations are presented in Section 4,which are used to verify and illustrate the theorems of Section 3.In Section 5,we present the conclusion and discuss future directions of this research.
2.Stochastic tumor–immune system with periodic treatment
In this section,the Kuznetsov–Taylor model[4]and its modified version by Galach[17]are introduced.The Kuznetsov–Taylor model describes the response of effector cells to the growth of tumor cells and takes into account the penetration of tumor cells by effector cells,which simultaneously causes the inactivation of effector cells.The Kuznetsov–Taylor model reads

where s is the normal(i.e.,not increased by the presence of the tumor)rate of the flow of adult effector cells into the tumor site in units of cells per day,p and g are positive constants in the function F(E,T)=pE T/(g+T)that describes the accumulation of effector cells in the tumor site,p is in units of day−1and g is in units of cells.m denotes the coefficient of inactivation of effector cells during the formation and decomposition of EC-TC compounds and is in units of day−1·cells−1. d is the coefficient of the destruction and migration of effector cells and is in units of day−1.a is the coefficient of the maximal growth of tumor and is in units of day−1.b−1is the environment capacity,and b is in units of cells−1.n represents the inactivation rate of tumor cells due to the immune system response and is in units of day−1·cells−1.The dimensionless form of the model is
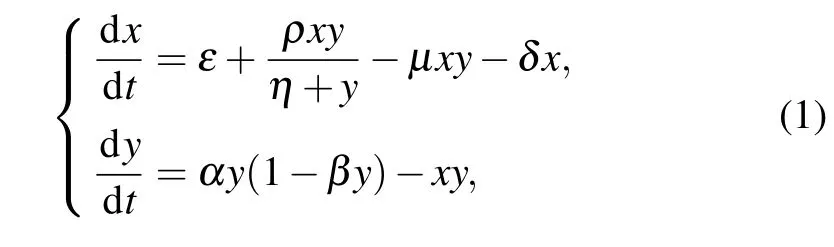
where x=E/E0,y=T/T0,ε=s/(nE0T0),ρ=p/(nT0), η=g/T0,µ=m/n,δ=d/(nT0),α=a/(nT0),β=bT0,and E0=T0=106cells.
In 2003,Galach proposed the modified version of model (1),which reads

where x denotes the dimensionless density of effector cells;y stands for the dimensionless density of the population of tumor cells;ε,δ,α,1/β have the same meanings as those in Eq.(1),and ω represents the immune response to the appearance of the tumor cells(i.e.,immune coefficient).In this paper, we consider the case of ω>0,which means that the immune response is positive.
System(2)always has the equilibrium
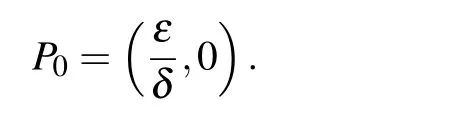
If ω>0 and αδ<ε,then P0is the unique equilibrium of model(2)and it is globally stable.If ω>0 and αδ>ε,then P0is unstable and there is an equilibrium
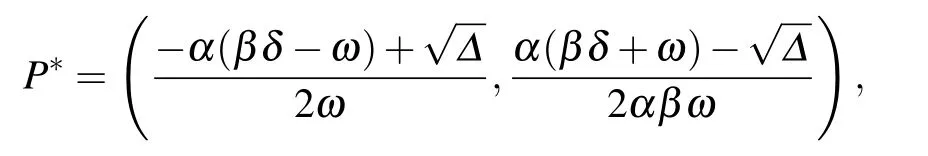
which is globally stable.Here Δ=α2(βδ−ω)2+4αβεω.
In fact,the growth of tumor cells is influenced by many environmental factors,[18]e.g.,the supply of oxygen and nutrients,the degree of vascularization of tissues,the immunological state of the host,chemical agents,temperature,etc.So, it is inevitable to consider the tumor–immune system competition model with environmental noises.In this paper,taking into account the effect of randomly fluctuating environment, we assume that the fluctuations in the environment mainly affect the immune coefficient ω,

where B(t)is the standard Brownian motion with B(0)=0, and the intensity of white noise σ2>0.We are interested in the stochastic responses of the tumor immune system driven by a controllable therapy.Here,the influence of the therapeutic factors is studied by considering a periodic treatment (chemo-or radiation-therapy).The treatment scheme[19]can be expressed as
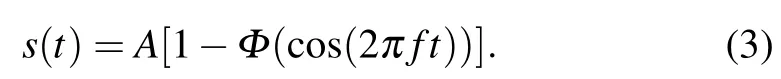
Here Φ stands for the Heaviside function reflecting the on-off switch of the cyclic treatment performed with the intensity A and frequency f.Now the tumor–immune system competition model with environmental noise and periodic treatment can be rewritten as
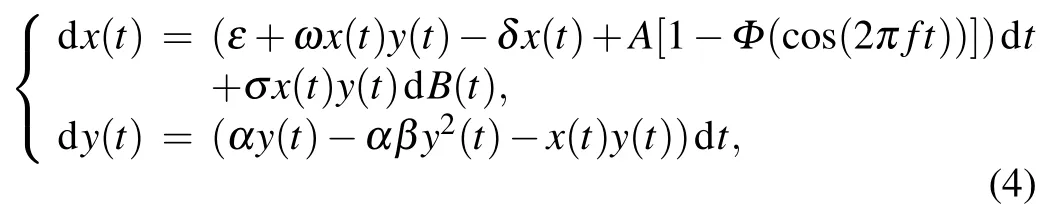
where all the parameters are positive and bounded.For convenience,we define the following notions:
3.Theoretical analysis of extinction and persistence under periodic treatment
Our primary interests in tumor dynamics are the extinction and survival of tumors.In order to study the extinction and survival,we need some appropriate definitions about extinction and persistence.Here we adopt the concepts of extinction and strong persistence in the mean.[20]In addition,some of our proofs are motivated by the works of Liu,[20]Mao,[21]and Jiang.[22]Some useful definitions are as follows:
1)The tumor cells y(t)will go to extinction a.s.if limt→+∞y(t)=0.
2)The tumor cells y(t)will be strongly persistent in the mean a.s.if〈y(t)〉∗>0.
Next we establish the sufficient conditions of extinction and persistence for our model.
Lemma 1 For any positive initial value(x0,y0),if 0<x0<1/β,the solution of Eq.(4)obeys
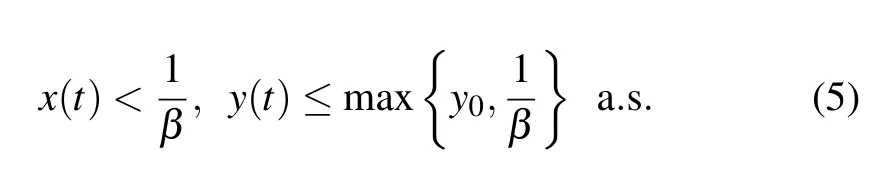
Proof According to the second equation of model(4),we have
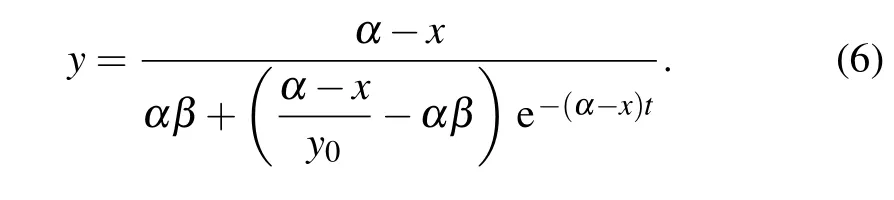
Firstly,we discuss y for x in different value ranges.
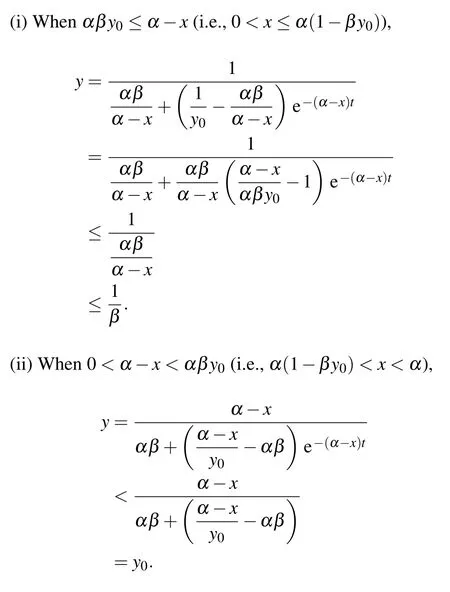
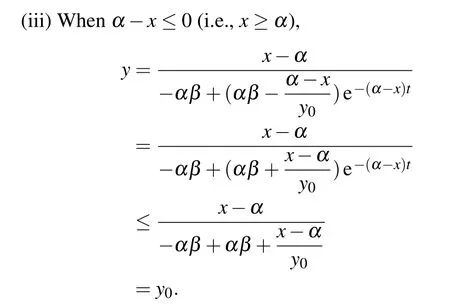
Consequently,we have proved y(t)≤max{y0,1/β}.Then we will show that x(t)is bounded.Applying the Ito’s formula[23]to the first equation of model(4),

Integrating both sides from 0 to t,we obtain
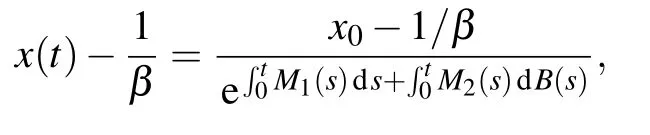
where

Therefore,

That is to say if x0<1/β,then x(t)<1/β for all t>0.
Lemma 2 Let f∈C[[0,∞)×Ω,(0,∞)]and F(t)∈C([0,∞)×Ω,R).If there exist positive constants λ0,λ,and T such that
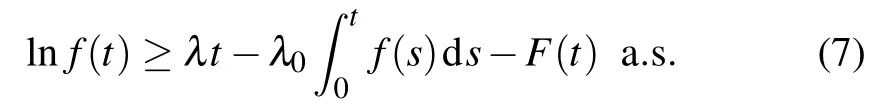
for all t≥T,and limt→∞F(t)/t=0 a.s.,then
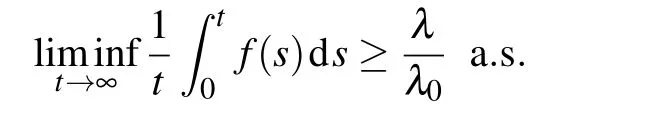
Proof The proof is similar to that of lemma in Ref.[22]. Note that limt→∞F(t)/t=0 a.s.;then for arbitrary k>0,there exists a T0=T0(ω)>0 and a set Ωksuch that P(Ωk)≥1−k and F(t)/t≤k for all t≥T0,ω∈Ωk.Let¯T=max{T,T0} and
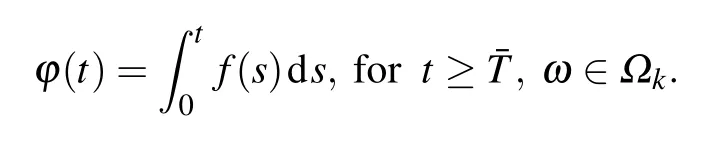
Since f∈C[[0,∞)×Ω,(0,∞)],then ϕ(t)is differentiable ona.s.,and

Taking the limit inferior of both sides and applying L’Hospital’s rule on the right-hand side of this inequality,we obtain
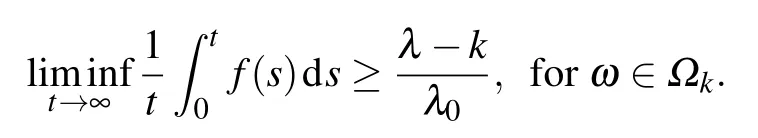
Letting k→0 yields

Theorem 1 For any positive initial value(x0,y0),particularly,when x0<1/β,equation(4)has a positive unique global solution(x(t),y(t))on t≥0 a.s.
Proof To obtain a unique global solution for any given initial value,the coefficients of the equation are generally required to satisfy the linear growth condition and local Lipschitz condition.[24]However,the coefficients of model(4)do not satisfy the linear growth condition,so the solution may explode in a finite time.Since the coefficients of Eq.(4)are locally Lipschitz continuous for any given initial value(x0,y0)∈,there is a unique maximal local solution(x(t),y(t))on t∈[0,τe],where τeis the explosion time.[24]To show that this solution is global,we only need to show τe=∞.To this end,let k0>0 be sufficiently large so that x0,y0all lie within the interval[1/k0,k0].For each integer k≥k0,we define the stopping time τk=inf{t∈[0,τe]:min{x(t),y(t)}≤1/k or max{x(t),y(t)}≥k}.Clearly,τkis increasing as k→∞.Set τ∞=limk→+∞τk,thus τ∞≤τea.s.In other words,we only need to prove τ∞=∞.If this statement is false,there exists constants T>0 and ε∈(0,1)such that P{τ∞<∞}>ε. Thus there is an integer k1>k0such that
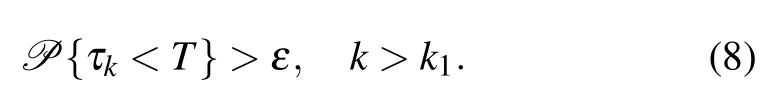
Define a C2-function V:→R+by V(x,y)=(x−1−ln x)+ (y−1−ln y).The nonnegativity of this function can be seen from u−1−ln u≥0,∀u>0.Let k≥k0and T>0 be arbitrary.Applying the Itˆo’s formula,we have
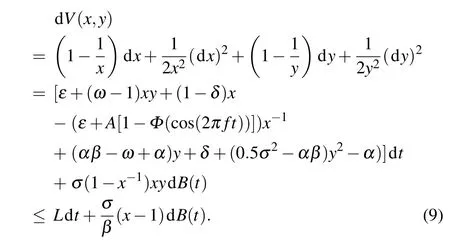
Here,L is a positive constant and in the proof of the last inequality,we have used Lemma 3(i.e.,for∀t≥0,x(t)and y(t) are bounded).The inequality(9)implies
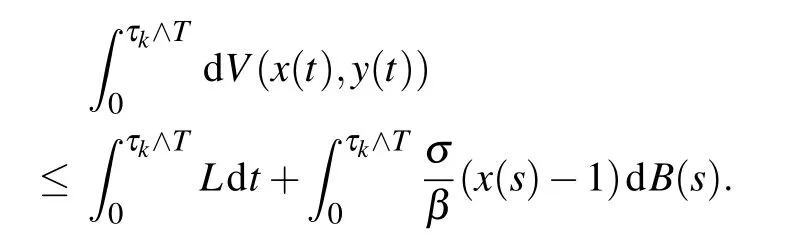
Taking expectation on both sides of the above inequality,we can obtain

Let Ωk={τk∧T},then by inequality(8),we have P(Ωk)≥ε. Note that for any ω∈Ωk,x(τk,ω),y(τk,ω)equals either k or 1/k,hence V(x(τk,ω),y(τk,ω))is no less than min{2(k−1−ln k),2(1/k−1+ln k),k+1/k−2)}.By formula(10)we have
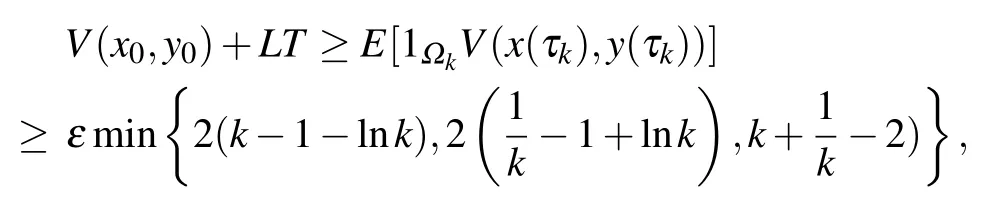
where 1Ωkis the indicator function of Ωk.Let k→∞,there exists the contradiction∞>V(x0,y0)+LT=∞,which completes the proof.
Remark 1 In order to guarantee the existence and uniqueness of the solution of model(4),we discuss the extinction and persistence of y(t)under the condition x0<1/β below.
Theorem 2 Let(x(t),y(t))be the solution of system(4) with positive initial value(x0,y0),if αδ−ε<A/2,then
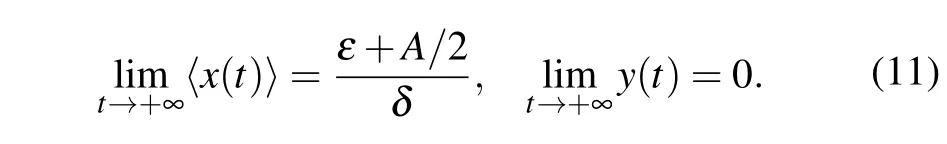
Proof An integration of the first equation of model(4) yields
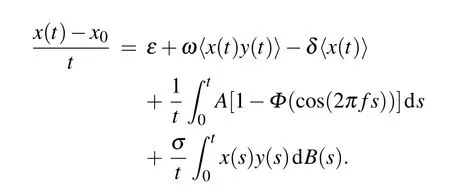
We compute

where

which is a local continuous martingale and N1(0)=0.Moreover
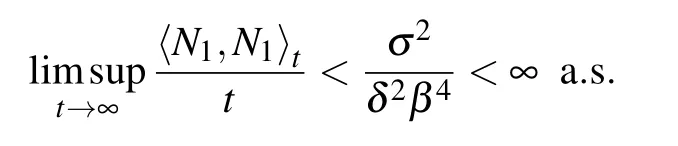
By strong law of large numbers for local martingales,[24]we obtain

Taking the limit inferior of both sides of inequality(12),we have
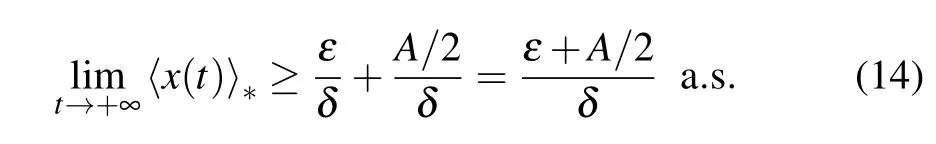
Applying the Itˆo’s formula to the second equation of model(4) yields
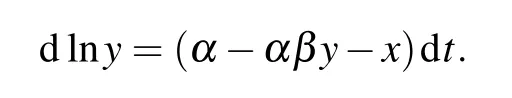
Integrating this from 0 to t and dividing by t on both sides,we have

Taking the limit superior of both sides of inequality(15)and substituting inequality(14)into inequality(15)yield
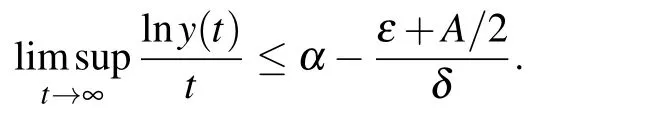
If the condition αδ−ε<A/2 is satisfied,then
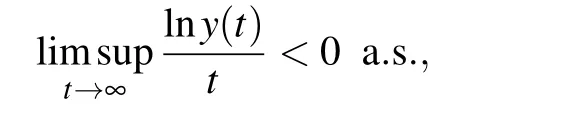
which implies
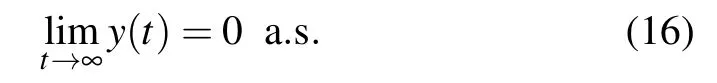
Applying the Itˆo’s formula to the first equation of model(4) leads to
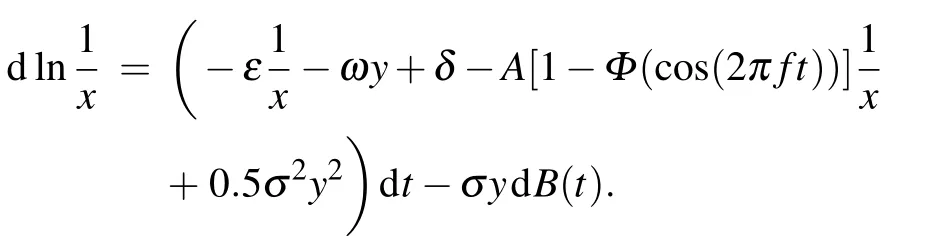
Integrating this from 0 to t,we have

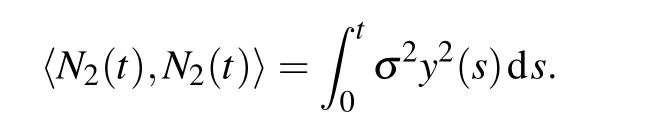
By virtue of the exponential martingale inequality,[24]for any positive constants T,a,and b,we have

Choosing T=n,a=1,and b=2ln n,we obtain
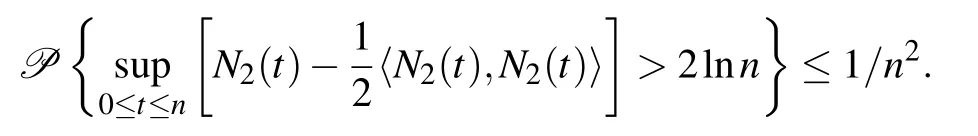
An application of Borel–Cantelli lemma[22]yields that for almost all ω∈Ω,there is a random integer n0=n0(ω)such that for n≥n0,
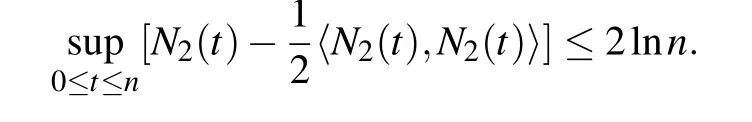
That is to say,

for all 0≤t≤n,n≥n0a.s.Substituting the above inequality into inequality(17)leads to

Theorem 3 If δα−ε>A/2,then the tumor cells y(t) will be almost surely strong persistent in the mean.
Proof An integration of system(4)is

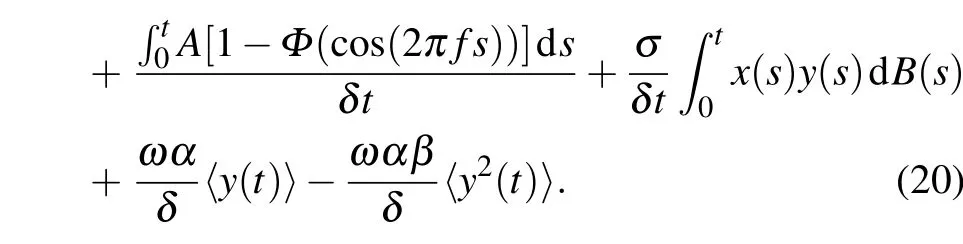
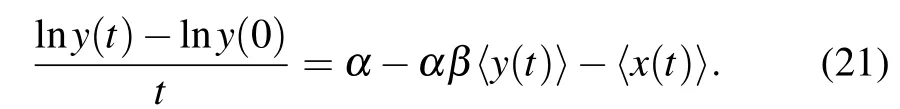
Substituting Eq.(20)to Eq.(21)yields


Consequently,we can derive that if δα−ε>A/2,then〈y(t)〉∗>0 a.s.
4.Simulations and discussion
In this section,we use the Euler–Maruyama numerical algorithm mentioned by Higham[25]to support our results.The parameters in model(4)are chosen as α=1.636,β=0.002, δ=0.3743,ε=0.5181,and ω=0.0115,which are approximated to the experimental values.[4,17]
Figure 1 shows the simulation results of Theorem 2. Clearly,the parameters satisfy the condition αδ−ε<A/2.In view of Theorem 2,the tumor cells y(t)will go to extinction, and the effector cells x(t)have the property limt→+∞〈x(t)〉= (ε+A/2)/δ=1.785.Figure 1 confirms the results of Theorem 2.

Fig.1.(color online)Solutions of model(4)with periodic treatment s(t)=A[1−Φ(cos(2π ft))]for A=0.3,σ=0.03,f=0.05,step size Δt=0.01,and initial value(x(0),y(0))=(1.5,25).
Figure 2 shows the simulation results of Theorem 2.In Fig.2,it is clear that the parameters of the example meet the condition δα−ε>A/2.According to Theorem 2,the tumor cells y(t)will be almost surely strongly persistent in the mean. It can be seen from Fig.2 that the tumor cells will decrease firstly and then exhibit a period-like evolution at a relative low concentration under periodic treatment,but do not tend to zero.This phenomenon implies that the tumor cells could be suppressed by the periodic treatment but not be completely eliminated when the intensity of the treatment is not enough to cure the tumor,i.e.,the tumor cells could be controlled and will not deteriorate in this case.Moreover,it can be seen that as long as the conditions of persistence δα−ε>A/2 are satisfied,the tumor cell will be strongly persistent in the mean almost surely when the model is with noise.And,the tumor cells will also be persistent or survival when the model is without noises.The difference is that the persistence of the former is in the sense of the mean,which is random;while the persistence of the latter is expressed as persistence or survival, which is deterministic.
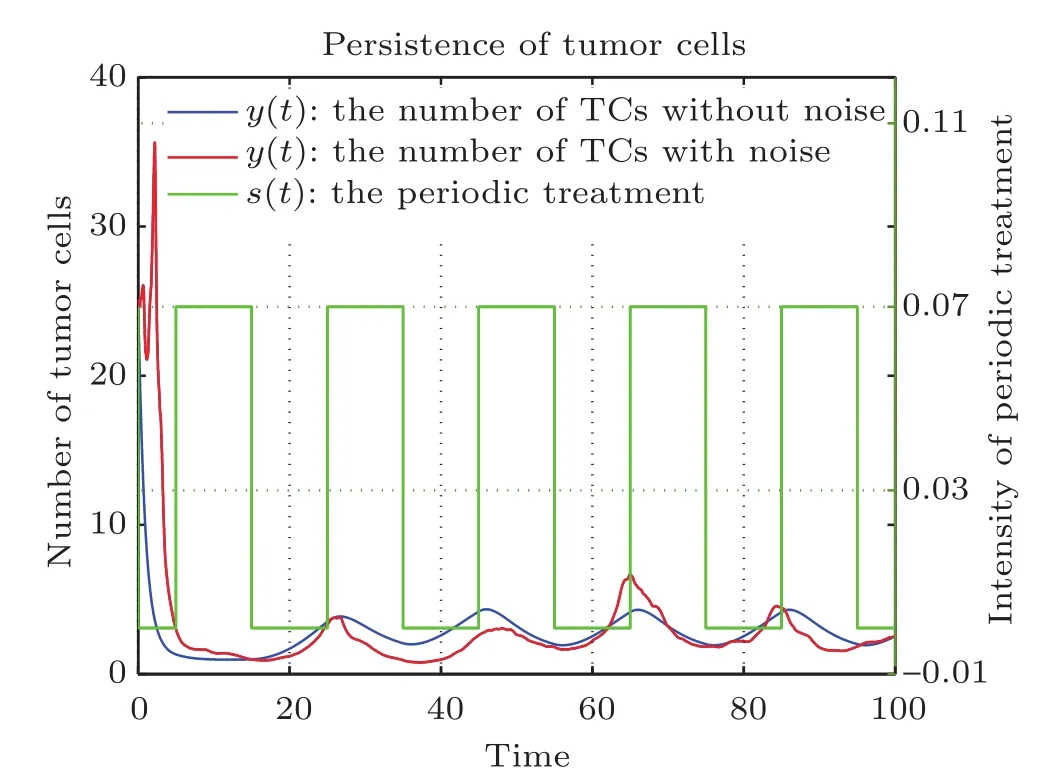
Fig.2.(color online)Solutions of model(4)with periodic treatment s(t)=A[1−Φ(cos(2π ft))]for A=0.07,σ=0.03,f=0.05,step size Δt=0.01,and initial value(x(0),y(0))=(1.5,25).
Figure 3 shows the evolution of tumor cells y(t)as a function of time t for three different values of A=0.07,0.3,3. Clearly,when A is 0.07,it satisfies the condition δα−ε>A/2.According to Theorem 2,the tumor cells y(t)will be strongly persistent in the mean.With increasing strength of the treatment,A is taken as 0.3 or 3,they satisfy the condition αδ−ε<A/2.According to Theorem 2,the tumor cells y(t) will tend to be extinction.Moreover,by comparing curves(ii) and(iii),we find that the tumor cells will be extinct faster with the increase of the treatment intensity A.This behavior indicates that increasing the intensity of the treatment is beneficial to accelerate the extinction of the tumor cells.
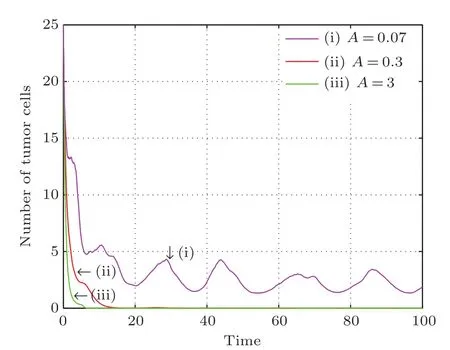
Fig.3.(color online)Solutions of tumor cells for σ=0.03,f=0.05,step size Δt=0.01,and initial value(x(0),y(0))=(2.6,25).
5.Conclusion
We study stochastic responses of a tumor–immune system competition model with environmental noise and periodic treatment.Firstly,the environmental noise(Gaussian white noise)is taken into account and the periodic treatment is regarded as a Heaviside function.Then,sufficient conditions for extinction and strong persistence in the mean of tumor cells are derived by constructing Lyapunov functions.The detail results and biological significance are as follows:
(A)If αδ−ε<A/2,then the effector cells x(t)have property limt→+∞〈x(t)〉=(ε+A/2)/δ,and the tumor cells y(t)will go to extinction a.s.
(B)If αδ−ε>A/2,then the tumor cells y(t)will be strongly persistent in the mean a.s.
According to the theorems and figures,the extinction and survival of the tumor cells rely on the strength of the periodic treatment.With the increasing intensity of the periodic treatment,the tumor cells will experience the process from strongly persistence in the mean to extinction.In addition,the synchronization effect between the environmental noises and the periodic treatment on the tumor–immune system competition model is obtained by strict proof and simulation.Our theoretical results will be beneficial to design more effective and feasible treatment therapies.
Some interesting questions deserve further investigations. For example,in our model,we assume that fluctuations in the environment mainly affect the immune coefficient ω.It is interesting to study what happens if it affects other parameters of the tumor–immune system.Another question of interest is to consider the stability in distribution(e.g.,Refs.[26]and[27]) and time delay(e.g.Ref.[28])of the tumor–immune system.
[1]Parish C R 2003 Immunol.Cell.Biol 81 106
[2]Smyth M J,Godfrey D I and Trapani J A 2001 Nat.Immunol.2 293
[3]Rosenberg S A,Spiess P and Lafreniere R 1986 Science 233 1318
[4]Kuznetsoz V A,Makalkin I A,Taylor M A and Perelson A S 1994 Bull. Math.Biol 56 295
[5]Kirschner D and Panetta J C 1998 J.Math.Biol 37 235
[6]Wang K K and Liu X B 2013 Chin.Phys.Lett 30 070504
[7]Yang Y G,Xu W,Sun Y H and Gu X D 2016 Chin.Phys.B 25 020201
[8]Zhong W R,Shao Y Z and He Z H 2006 Phys.Rev.E 73 060902
[9]Albano G and Giorno V 2006 J.Theor Biol 242 329
[10]Lenbury Y,Triampo Wannapong,Tang IMand Picha P 2006 J.Korean. Phys.Soc 49 1652
[11]Ferrante L,Bompadre S,Possati L and Leone L 2000 Biometrics 56 1076
[12]Thibodeaux J J and Schlittenhardt T P 2011 Bull.Math.Biol.73 2791
[13]Sotolongo-Costam O,Molina L M,Perez D R,Antranz J C and Reys M C 2003 Physica D 178 242
[14]Ideta A M,Tanaka G,Takeuchi T and Aihara K 2008 J.Nonlinear Sci. 18 593
[15]Li D X,Xu W,Guo Y and Xu Y 2011 Phys.Lett.A 375 886
[16]Aisu R and Horita T 2012 Nonlinear Theory and Its Applications,IEICE 3 191
[17]Galach M 2003 Int.J.Appl.Math.Comput.Sci.13 395
[18]Fiasconaro A,Spagnolo B,Ochabmarcinek A and Gudowskanowak E 2006 Phys.Rev.E 74 041904
[19]Fiasconaro A,Ochab-Marcinek A,Spagnolo B and Gudowska-Nowak E 2008 Eur.Phys.J.B 65 435
[20]Liu M and Wang K 2011 J.Math.Anal.Appl.375 443
[21]Mao X,Marion G and Renshaw E 2002 Stoch.Proc.Appl.97 95
[22]Zhao Y,Jiang D and O’Regan D 2013 Physica A 392 4916
[23]Evans L C 2013 An Introduction to Stochastic Differential Equations (New York:Amer Mathematical Society)pp.77–79
[24]Mao X 1997 Stochastic Differential Equations and Applications (Chichester:Horwood)pp.31–84
[25]Higham D J 2001 SIAM Rev.43 525
[26]Liu M and Bai C 2016 Appl.Math.Comput.284 308
[27]Liu M and Bai C 2016 Appl.Math.Comput.276 301
[28]Jin Y F and Xie W X 2015 Chin.Phys.B 24 110501
26 February 2017;revised manuscript
9 May 2017;published online 24 July 2017)
10.1088/1674-1056/26/9/090203
∗Project supported by the National Natural Science Foundation of China(Grant Nos.11402157 and 11571009),Shanxi Scholarship Council of China(Grant No.2015-032),Technological Innovation Programs of Higher Education Institutions in Shanxi,China(Grant No.2015121),and Applied Basic Research Programs of Shanxi Province,China(Grant No.2016021013).
†Corresponding author.E-mail:dxli0426@126.com
©2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn
- Chinese Physics B的其它文章
- Relationship measurement between ac-Stark shift of 40Ca+clock transition and laser polarization direction∗
- Air breakdown induced by the microwave with two mutually orthogonal and heterophase electric field components∗
- Collective motion of active particles in environmental noise∗
- Temperature dependence of heat conduction coefficient in nanotube/nanowire networks∗
- Analysis of dynamic features in intersecting pedestrian flows∗
- Heat transfer enhancement in MOSFET mounted on different FR4 substrates by thermal transient measurement∗

