Assessment of cortical bone fatigue using coded nonlinear ultrasound∗
Duwei Liu(刘度为),Boyi Li(李博艺),Dongsheng Bi(毕东生),Tho N.H.T.Tran,Yifang Li(李义方),3,Dan Liu(刘丹),Ying Li(李颖),and Dean Ta(他得安),,‡
1Center for Biomedical Engineering,School of Information Science and Technology,Fudan University,Shanghai 200433,China
2Academy for Engineering and Technology,Fudan University,Shanghai 200433,China
3Human Phenome Institute,Fudan University,Shanghai 200433,China
Keywords:nonlinear ultrasonic Lamb wave,bone fatigue,chirp code,pulse inversion
1.Introduction
Bone is an important part of the human body structure.It protects internal organs and supports the body to complete all kinds of physical activities.Just like various components used in industrial production and other fields,the bones will suffer from fatigue due to a long time and high strength stress in the process of service.[1,2]For example,the weight-bearing bones will be bent while the human body is loaded or doing some strenuous exercise.Once the bending or damage exceeds a limit,the microdamage of the internal structure cannot be repaired efficiently.The accumulation of microdamage can lead to bone fatigue in severe cases,making it one of the main reasons for overuse fracture.[3]It is of great demand and significance to evaluate the microdamage or fatigue level in the bone to prevent further deterioration.
The traditional methods of monitoring bone health conditions are using computer tomography(CT)or dual x-ray absorptiometry(DXA),which are convincible ways to evaluate bone fatigue and fracture.Still,they have shortcomings such as radiation and relatively low resolution.Although the synchrotron radiation micro-computed tomography(SR-µCT)can effectively assess the micro-cracks at a micro-scale resolution,[4–7]it cannot be used to detect microdamage in vivo due to its destructive features.Ultrasound technique has the advantages of non-ionizing radiation and high sensitivity to defects,making it a reliable approach to assess bone health conditions.The ultrasound technique for evaluating bone fatigue can be divided into two categories:linear ultrasound and nonlinear ultrasound,depending on the relationship between stress and strain.The parameters related to bone properties(such as thickness,[8]bone mineral density,[9]and porosity[10])of linear ultrasound are speed of sound(SOS)and broadband ultrasound attenuation(BUA).But these two parameters are not highly correlated to bone microdamage,[11,12]which means they may be incapable to evaluate the damage of bone in the early stage.The nonlinear ultrasonic technique provides us with a novel way of detecting bone microdamage.It was firstly applied in industrial nondestructive testing because of the high sensitivity to micro defects such as micro-cracks,[13–16]dislocations,[17,18]and precipitates.[19,20]The physical mechanism of nonlinear behavior between wave and micro-cracks is that the incident wave is distorted while penetrating through the micro-crack,resulting in a nonlinear response,which is so-called contact acoustic nonlinearity(CAN).[21]Besides,the second and third-order elastic coefficients near the micro-cracks and within the crack differ,[22]thus amplifying the nonlinear response.For crystals,the displacement of dislocations also contributes to the nonlinear behavior of materials,since there is a transformation of stress.However,the aforementioned microdamages do not significantly change the Young modulus and the Poisson ratio,which means they cannot be detected by conventional linear methods.The main methods of nonlinear ultrasound technique consist of nonlinear elastic wave spectroscopy(NEWS),nonlinear resonance ultrasound spectroscopy(NRUS),[23]dynamic acoustic elasticity test(DAET),[24,25]higher harmonic generation,[26–28]and nonlinear ultrasound vibro-modulation(NUVM).[29]
As the nonlinear ultrasound research goes further,some researchers have pointed out that nonlinear ultrasonic nondestructive testing can be applied not only for the health detection of metal materials[30]but also for composite materials[31]and even bones.Muller et al.showed that nonlinear ultrasound can be used to detect cumulative damage to human bones in 2007.[23]Furthermore,nonlinear ultrasound is used to monitor the microdamage of bone,[32]including cortical bone[4,33]and cancellous bone.[34]However,the relationship between second harmonic generation in bone and fatigue accumulation has not been fully investigated experimentally.Haupert et al.firstly reported the nonlinear elastic hysteretic behavior(assessed by the nonlinear elastic parameterαf)and microdamage accumulation in real bone samples.[4]To generate microdamage in bone,a four-point-bending fatigue cycling experiment was conducted.After each cycle of bending,the nonlinear hysteretic parameter and the biomechanical parameters of cortical bone are measured.The number and size of micro-cracks in the specimen after each cycle is also monitored by SR-µCT.Their results suggested that the damage steps had a statistically significant effect on the nonlinear hysteretic parameterαfmeasured by NRUS.These studies are mainly based on analyzing bulk waves in bone structure.Since second harmonic generation is also part of nonlinear ultrasound technique and has a wide range of applications,this study aims at trying to apply this method to the detection of microdamage accumulation in bone by coding and decoding to increase the signal-to-noise ratio.
In summary,the nonlinear ultrasonic technique has its unique advantages in nondestructive testing and it is entirely feasible in bone fatigue evaluation.Yet,despite the commonality in the microdamage assessment of bone and industrial materials(such as aluminum and steel),there are some difficulties in practical application.It is known that the bone is a porous medium,the attenuation of ultrasound in bone is relatively high and tends to result in a low SNR.Besides,since the nonlinear effect is weak when the material damage is in the early stage,we cannot accurately extract the features of nonlinearity from a low amplitude signal.[35]The general approach to solve the problem is to increase the amplitude of the excitation significantly to get a higher amplitude of the second harmonic,which puts higher requirements on both the excitation voltage and transducer.
The objective of this work is to determinate the relationship between second harmonic accumulation phenomenon and bone fatigue,we had an experimental observation on the nonlinear guide wave in the bone.The progressive fatigue loading experiment is also conducted,verifying that the microdamage level is indeed closely related to the nonlinearity of the bone.To improve the SNR of second harmonics in bone,we applied a signal coding method to the nonlinear measurement.The idea of coding was originally used in the radar system and has been gradually applied to ultrasonic detecting.[36,37]The coding of the signal can be divided into linear frequency modulated(FM)signals or nonlinear FM signals,and the phase codes.Depending on the type of carrier signal and modulating signal.Compared to traditional tone burst excitation,coded excitation has a longer duration in the time domain.[38]Besides,the SNR of the receiving signal can be improved through decoding.The main works of this paper are listed below:
(i)A weighted chirp signal is applied to the ultrasonic excitation of guided waves in bone,meanwhile,the SNR of the received signal gets improved through decoding.
(ii)The progressive damage experiment is conducted on cortical bone plates,with the coding ultrasound method being applied to the nonlinearity measurement.The results verified that the fatigue level of cortical bone can be characterized by the nonlinearity of bone efficiently.
The rest of the paper is organized as follows.Section 2 introduces the fundamental theories and methods.The material and experimental setup are illustrated in Section 3.Section 4 and Section 5 present the experiment results and discussions.The conclusion is given in Section 6.
2.Theory and methods
2.1.Dispersion of Lamb wave
This paper mainly focuses on the second harmonic component generation while ultrasound propagating in a bone plate,i.e.,the nonlinear Lamb wave.
The mathematical equation of ultrasound propagating in an isotropic solid plate can be expressed as[39]
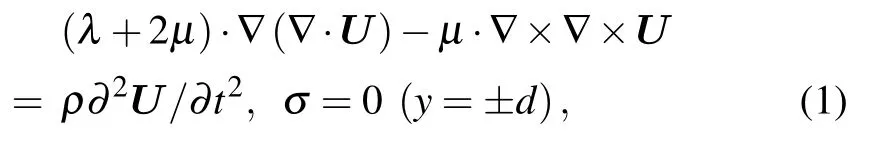
where U denotes the displacement of a single point,ρis the density of the material,t stands for time,σis the stress of the material,λandµare the lame coefficients.By solving Eq.(1),we can get the dispersion equation of the Rayleigh–Lamb wave[39]

where k is the wave-number.the coefficients p and q can be given by
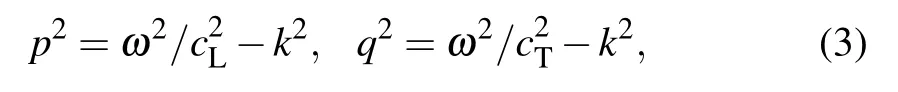
with cLand cTbeing the longitudinal and shear velocities of the ultrasound.According to Eqs.(2a)and(2b),the Lamb wave can be divided into the symmetric and antisymmetric modes,depending on the distribution of displacement.
2.2.Cumulative second harmonic generation and mode selection
The second harmonic fields of Lamb waves are complex because of their multimode and dispersion features.To observe an obvious nonlinear phenomenon,the second harmonic needs to meet the cumulative condition.As for the ultrasound excitation,it is also required to excite only the fundamental mode at the excitation end,ensuring that the other mode will not have interference to the generation of the second harmonic.
The cumulative harmonic Lamb wave generation requires phase synchronism and nonzero power flux.The first refers to the phase velocity matching condition:the phase velocity of the second harmonic mode at the second frequency must be identical to the phase velocity of the fundamental mode at the fundamental frequency;[40]the second condition means that the energy flux from the fundamental mode to the second harmonic mode is nonzero.[41]The energy flux is generated by the nonlinearity of the material itself,which is the driving force of the fundamental wave to the second harmonic.And the phase velocity matching condition ensures that the energy transfers from the fundamental to the second harmonic mode.
The phase–velocity dispersion curves for a 1-mm-thick cortical bone plate are shown in Fig.1,which were computed by the software Disperse(Imperial College,London,UK).The density of the cortical bone was 1900 kg/m3and the measured longitudinal velocity and the shear velocity were 3850 m/s and 1650 m/s respectively.According to previous research,[42]no matter the fundamental mode is symmetric or antisymmetric,the power flux is nonzero only for the case that the second harmonic mode is symmetric.In other words,the cumulation of the harmonic wave only occurs when the second mode is symmetric.The dashed lines stand for the symmetric double frequency modes,with the frequency axis scale reduced to half of the fundamental mode.In this way,the intersections with the primary dispersion curves represent phase matching.There are two intersections,as shown in Fig.1.The results show that mode pairs S1–S2 and S2–S4 can meet the cumulative harmonic wave condition at 1.78 MHz and 2.55 MHz,respectively.
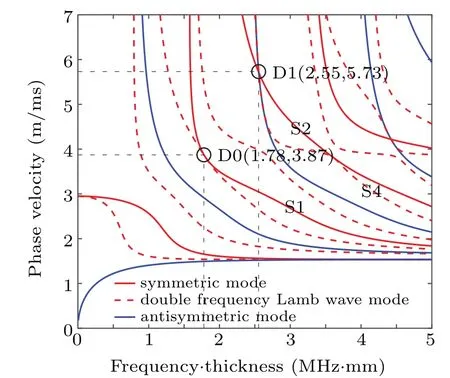
Fig.1.Phase–velocity dispersion curves of the fundamental Lamb waves and the second harmonic Lamb waves propagating in a 1-mm-thick cortical bone plate.
The mode pair S1–S2 was chosen as the fundamental and secondary modes,not only because they have a lower frequency at the phase matching point and higher frequency Lamb wave tends to generate severe dispersion,but also for the reason that the observation of the second harmonic requires a high efficiency of internal resonance to produce harmonics.For a plate-like material,the most efficient mode pair to generate cumulative harmonic Lamb wave is S1 and S2,[41]which refers to point D0 in Fig.1.
2.3.Weighted linear chirp ultrasound excitation
Linear chirp signal,as the name implies,refers to a sinusoidal signal for which the frequency linearly varies with time.As one of the most commonly used frequency modulation methods,the chirp signal is often applied as the excitation of ultrasound imaging.Because its center frequency and bandwidth,duration are adjustable compared to tone burst or phase-modulated signals.The chirp signal can be represented by
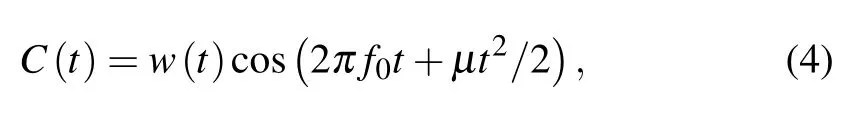
where w(t)is a window function,f0is the start frequency,µis a constant related to the frequency sweep bandwidth B over signal duration T,defined byµ=2πB/T.Typically,chirp excitation has wide application in the pulse-echo mode ultrasonic scenario,which is related to its need for axial resolution in ultrasound imaging.Nevertheless,some researchers have pointed out that chirp excitation can be applied for ultrasonic guided waves.[43–45]As long as the bandwidth of the desired excitation falls within that of the chirp,the corresponding response of the tone burst excitation can be separated from the chirp response signal.

Fig.2.(a)Time-domain of weighted linear chirp(fc=0.5 MHz,B=0.1 MHz,T=50µs),(b)spectrum of chirp,(c)time-domain of weighted tone burst excitation signal(f0=0.5 MHz,T=50µs),and(d)spectrum of tone burst.
Another reason for choosing chirp as the excitation in our work comes down to the properties of the cumulative second harmonic in nonlinear ultrasonic detection.Matsuda and Biwa[46]demonstrated by mode expansion analysis as well as numerical simulations that there is no strict frequency dependence in the generation of cumulative second harmonics.The second harmonic Lamb waves can be generated cumulatively when the phase velocity matching condition is satisfied in an approximate sense.
The chirp signal maintains the same amplitude over the entire time domain,which can be regarded as adding a rectangular window of amplitude 1(w(t)=1).For suppression of the peak sidelobe level,the signal is weighted by a Hanning window function.[47]The expression of w(t)in Eq.(2)is as follows:
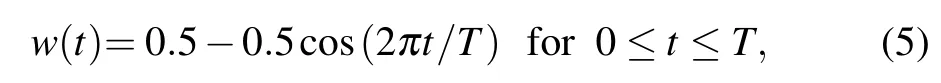
thus C(t)is a weighted linear FM signal.A Hanning windowed chirp and tone burst sinusoidal signal are shown in Fig.2.
2.4.Second harmonic extraction
It is a challenge to have an experimental observation of cumulative second harmonics in bone,especially when the propagation distance is relatively long.The attenuation in bone is so high that even though the fundamental frequency component is apparent,the interference of noise and second harmonic is strong.This paper is motivated by second harmonic imaging in ultrasound diagnosis,both of which have the demand of extracting the second harmonic signal as accurately as possible.The conventional method used for nonlinear Lamb wave measurements is hardware-filtering at the receiver side,which is inevitably limited by the fixed passband and stopband of the filter.Song et al.proposed three methods for coded tissue harmonic imaging(CTHI)in 2010 and 2011:bandpass filtering(BF),pulse inversion(PI),and pulse modulation(PM).[48,49]We choose pulse inversion as the method to extract the second harmonic.The principle of pulse inversion is that the transmitter emits two excitations of the opposite phase as follows:

where c+(t)stands for the baseline emission signal and c−(t)is an inverted replica of c+(t).For the inversed signal,the odd frequency components(fundamental,the third harmonic,etc.)have an inverted phase compared to the former.while the even frequency components(the second harmonic,etc.)have a 360-degree phase shift.Therefore,assuming the ultrasonic response system is linear,the components in the received signal can be expressed as follows:

where rnf(t)denotes the n-th frequency component.Summing these two received signals,it is theoretically possible to achieve the effect of suppressing the fundamental frequency component and increasing the magnitude of the second harmonic.
3.Materials and experimental setup
3.1.Experimental framework
The system framework is shown in Fig.3.A PC controlled the function generator to edit the excitation,which was amplified by a signal amplifier AG 1021(T & C Power Conversion,Inc,USA).The high voltage signal was sent to a 0.5-MHz PZT transmitting transducer(Valpey Fisher,USA).The ultrasound,propagating through the cortical bone plate,carried the information of the second harmonic waves and was measured by the receiving transducer.Since the second harmonic component was significantly weaker than the fundamental(the amplitude of the second harmonic component is almost 1% of the fundamental),the receiving transducer had a center frequency at approximately the second harmonic frequency,which made the first and second harmonic frequency amplitudes be detected simultaneously.A broadband PZT transducer centered at 1 MHz(V539-SM,OSSA,USA)was used as the receiver.An oscilloscope(DSOX1204G,Keysight,USA)was used for real-time display and acquisition of the received signals.
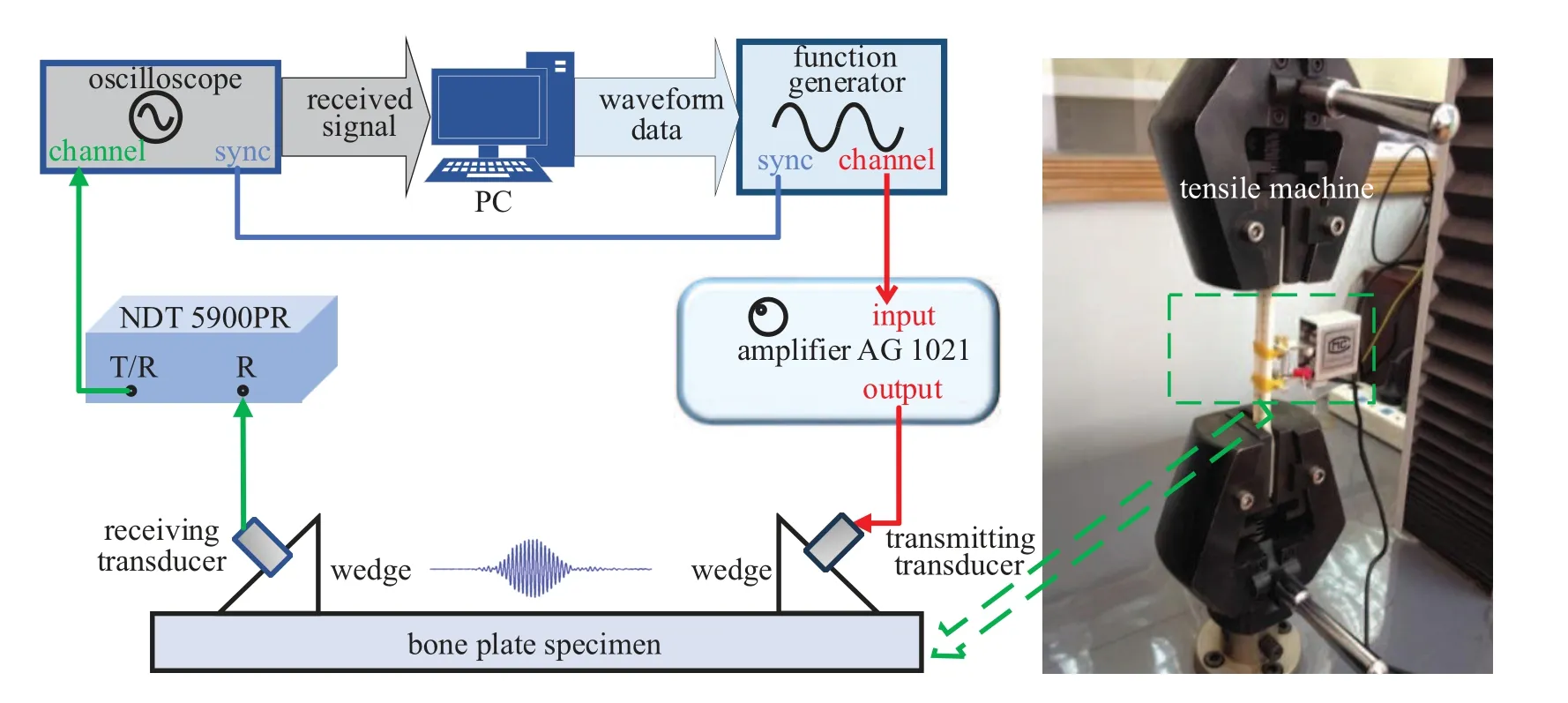
Fig.3.Structure of the nonlinear ultrasonic guide wave measurement system and fatigue loading on the cortical bone.
The transducer was glued to a plexiglass wedge to avoid excitation of other modes because of the multimode feature of Lamb waves.According to Snell’s law
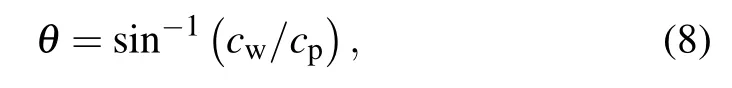
where cw=2650 m/s is the longitudinal wave velocity of the wedge and cp=3870 m/s is the phase velocity of the fundamental mode(seen in Fig.1,D0)in the material.According to Eq.(8),the calculated angleθof the transmit transducer should be around 43°,and the receiving transducer was placed at the same angle.
The procedures of nonlinear ultrasonic measurement experiments are as follows:the bone plate specimen was placed on a horizontal plane,and the transducers were coupled to the plexiglass wedges by liquid coupling,while the transmitting transducer converted the amplified voltage signal to ultrasound.After propagated through the plate specimen,the ultrasonic Lamb wave was then sensed by the receiving transducer.The oscilloscope is triggered synchronously by the function generator,while the received signal is observed in real-time,which was amplified by NDT 5900PR.
3.2.Bovine tibia plate in vitro and fatigue test
The experiment materials in this article were three cortical bone plates,the detailed parameters are listed in Table 1,with a density of 1900 kg/m3,which were polished from the bovine tibias obtained from a butcher shop.To explore the relationship between bone fatigue and nonlinearity,a fatigue loading experiment of the cortical bone plate was conducted.

Table 1.Dimensions of three bone specimens.
To simulate the early microdamage response of cortical bone,a tensile testing machine(WDW-25C,Hualong,China)was used to stretch the bone plate longitudinally,as shown in Fig.3.According to previous research,the tensile test has a better effect in inducing more microdamage than compression.[50,51]To avoid macroscopic damage while inducing microdamage,it is necessary to ensure the magnitude of tension is between the fatigue limit and the tensile strength of the bovine bone.The above requirements can be met at maximum stress of 34 MPa,[52]corresponding to a maximum force of 2000 N.The tension was set to 400 N as an initial force,and the rate of tension growth was 200 N/S.When the force reached 2000 N,it then decreased at the same rate.The process repeated until the set number of times was reached.
4.Results
4.1.Nonlinear Lamb wave measurement before fatigue loading
The nonlinearity measurement,as shown in Fig.3,was conducted on specimen#1 to provide a benchmark.The propagation distance ranged from 45 mm to 90 mm,with a step size of 5 mm.To compare the performances of the chirp and conventional tone burst excitation,we conducted separate experiments,with a consistent duration.As can be known from the frequency thickness product in Fig.1,the phase matching frequency of the tone burst signal is around 0.42 MHz.The center frequency of the chirp signal was set to 0.42 MHz and the bandwidth was 0.1 MHz.A 21-cycle Hanning window modulated sinusoidal signal was chosen as the tone burst excitation.Both these signals have a duration of 50µs to eliminate the influence of excitation time on the results.
The received signal at a propagation distance of 9 mm is shown in Fig.4.Figure 4(a)shows the result of the received weighted chirp signal,the pulse inversion(PI)result is given in Fig.4(b).Meanwhile,the received signal of tone burst excitation is shown in Fig.4(c).
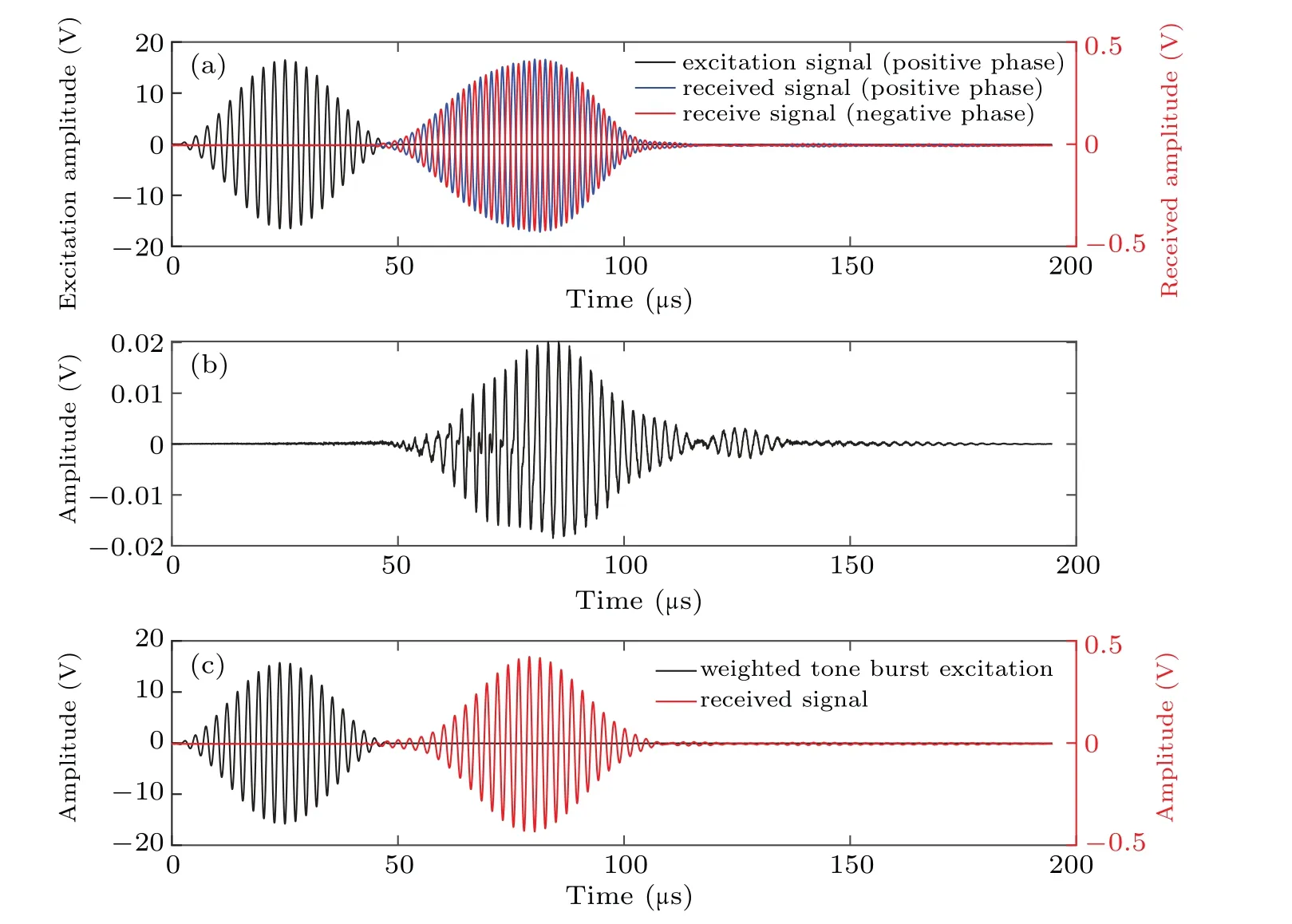
Fig.4.Received signals in two different modes of excitation at the distance of 90 mm before the fatigue loading:(a)result of weighted chirp excitation,(b)pulse inversion result,(c)result of weighted tone burst excitation.
There is no significant difference in the time domain between the two except for a longer signal duration after pulse inversion.Since the calculation of nonlinear acoustic parameter requires the values of the fundamental and the second harmonic signals,we investigate the effect of the weighted chirp signal on the second harmonic extraction in the frequency domain.
Figure 5 shows the spectra of the signal processed by the two methods.In Fig.5(a),the blue and green lines represent the spectra of the excitation waveform.While the spectra of the received weighted chirp signal and the received tone burst signal are marked with black and red lines.It is obvious that the second harmonic component in received signal is not caused by the excitation.Figure 5(b)demonstrated the spectra of the pulse inversion result and the received tone burst signal.By applying the pulse inversion method,the amplitude of the second harmonic can be improved effectively while the fundamental component is suppressed(as shown in Fig.5(a)).The improvement of the second harmonic is about 6 dB.Concerned about SNR of the received signal,when the weighted tone burst excitation was chosen,the SNR of the fundamental component is about 64 dB and the SNR of the second harmonic is about 19 dB.While applying pulse inversion of weighted chirp excitation,the SNR of the fundamental and the second harmonic signals are 49 dB and 36 dB respectively.
Furthermore,the nonlinear parameter at a single propagation distance is not so valuable for assessing the microdamage of material.We either concentrate on the variation of nonlinear parameters with the degree of microdamage at the same point or the cumulative effect with propagation distance.Specifically,the acoustic nonlinear parameters increase linearly with propagation distance when the second harmonic accumulation condition is satisfied.Therefore,we explore the effect of the chirp coding method on the fitting of this growth trend.
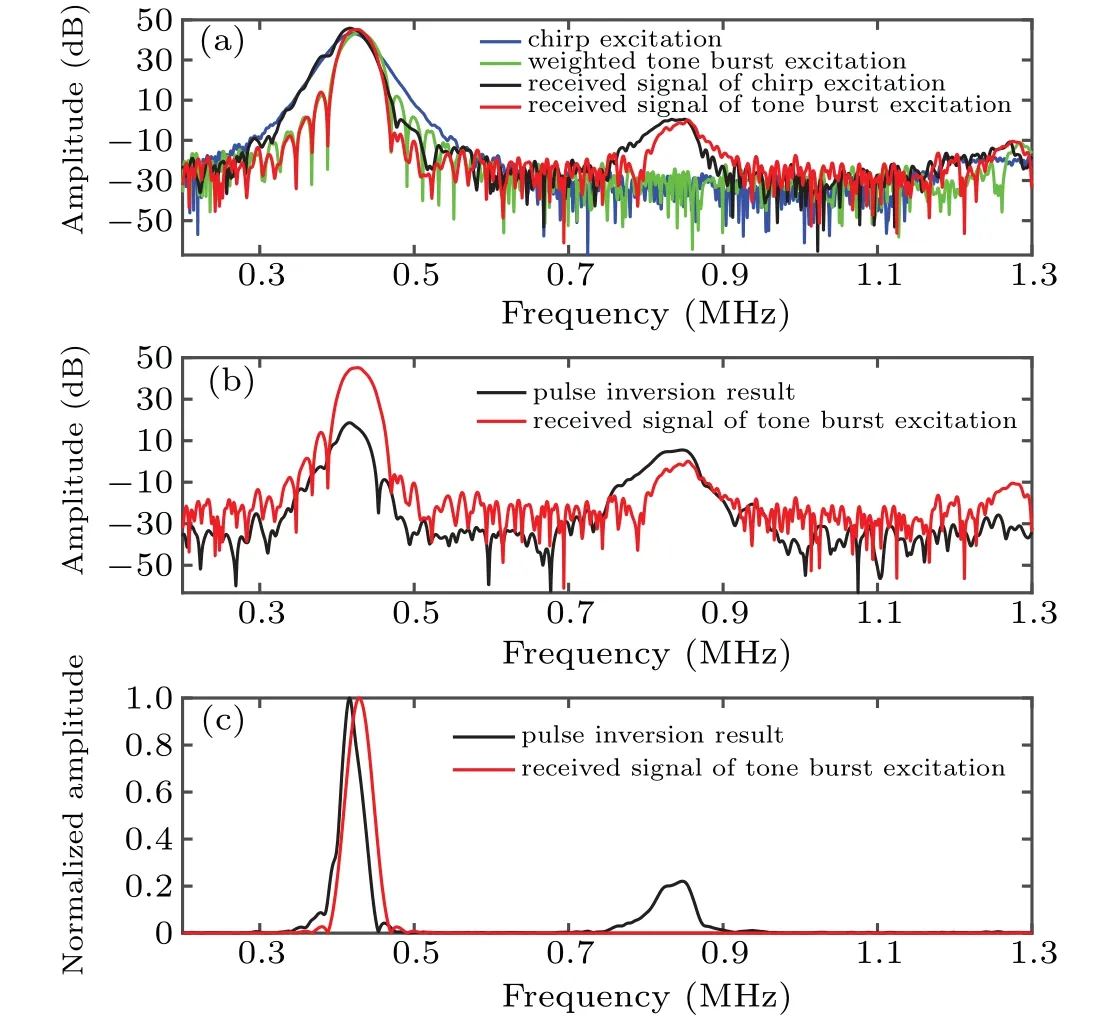
Fig.5.The spectra of excitation and received signals before fatigue loading:(a)spectrum of excitation and received signals,(b)spectrum of pulse inversion and tone burst excitation results,(c)normalized amplitude spectrum.
The same measurement was conducted on specimen #1 under different distances.After completing the measurements at the entire distance segment,the nonlinear parameters were calculated.Here,we give the results of the linear fit of the nonlinear parameters with propagation distance after applying the coding method and tone burst excitation,as shown in Fig.6.The nonlinear parameter is normalized to the maximum value.
As can be seen from Fig.6,for the conventional tone burst excitation,the correlation between the linear fitting curve(green solid line)and the experiment data(green triangle dot)is not significant.When the propagation distance is short,a linear growth trend can be obtained,but as the distance increases,the resolvability of the second harmonic decreases dramatically,leading to inaccurate calculation of the nonlinear parameters.For the weighted chirp excitation method,the correlation of the experimental data fit was high,R2=0.86(p<0.05).The linear growth of the nonlinear parameters with the propagation distance is also obvious.

Fig.6.The comparison of the cumulative effect of the nonlinear parameter in the specimen obtained by the two methods.
4.2.Nonlinear Lamb wave measurement after fatigue loading
To determine the level of bone fatigue,we define two stages of bone damage,corresponding to 5000 and 10000 fatigue loading cycles.
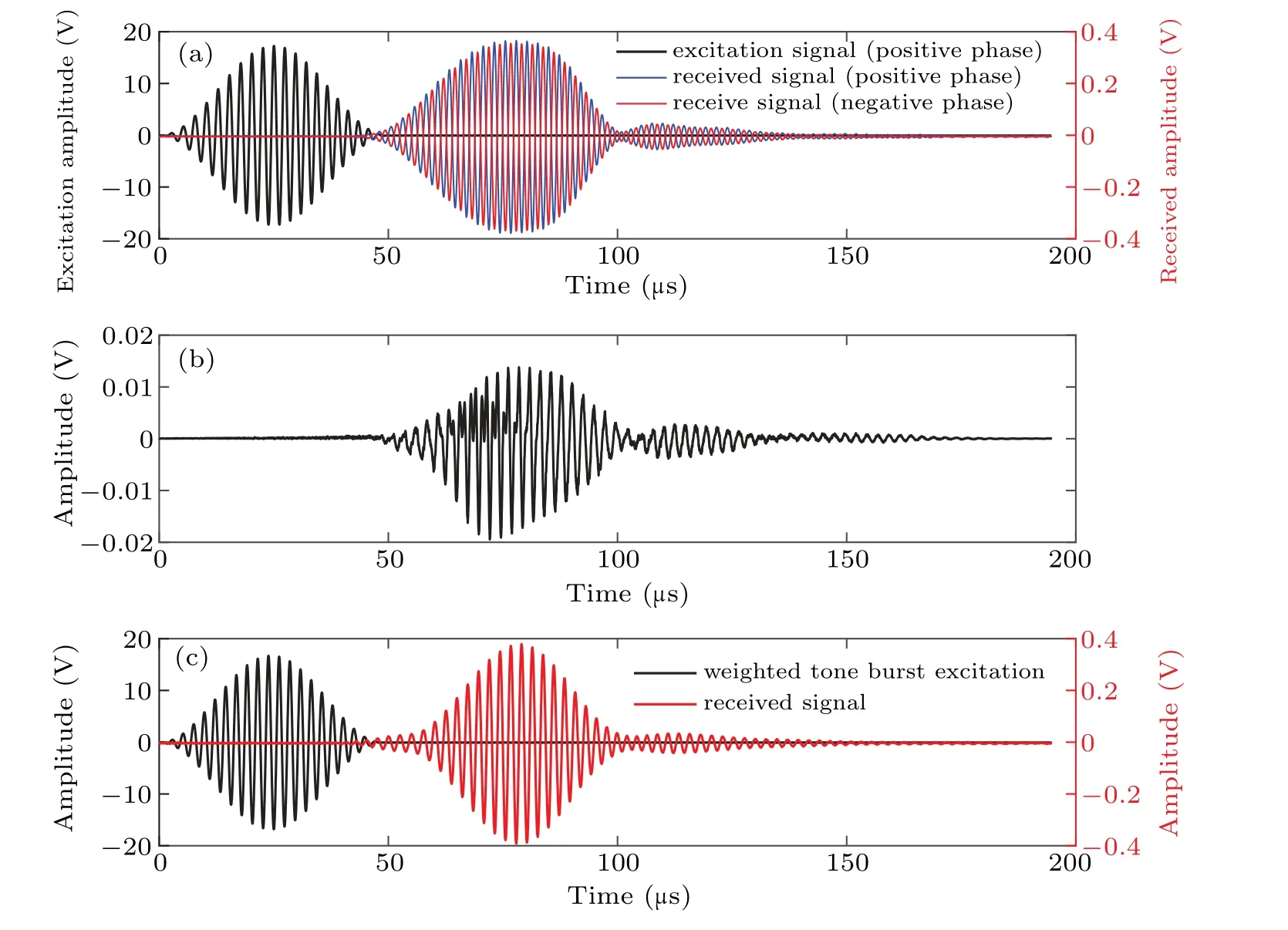
Fig.7.Received signals in two different modes of excitation at the distance of 90 mm after the fatigue loading:(a)result of weighted chirp excitation,(b)pulse inversion result,(c)result of weighted tone burst excitation.
The nonlinearity measurement was applied to the same bone plate at these two stages while the ultrasound excitation parameters remain unchanged.Figure 7 shows the received signals under the weighted chirp and tone burst excitation.
Figure 7(b)shows the summed signal by pulse inversion,the received signal of tone burst excitation is given in Fig.7(c).The result is consistent with the case without fatigue loading.
Figure 8(a)shows the spectra of the received signals after 10000 tensile loadings,including received signal of weighted chirp excitation(the black line),and received tone burst signal(the red line).The spectra of the pulse inversion result and the received tone burst signal are further compared in Fig.8(b)and Fig.8(c).The results indicate that the signal after pulse inversion still has a good performance in improving the second harmonic magnitude and SNR.
The SNR of received signal under weighted tone burst excitation was 59 dB and 18 dB,corresponding to the fundamental and the second harmonic components.For the received signal under weighted chirp excitation,the pulse inversion indeed improved the SNR of the second harmonic to 36 dB.
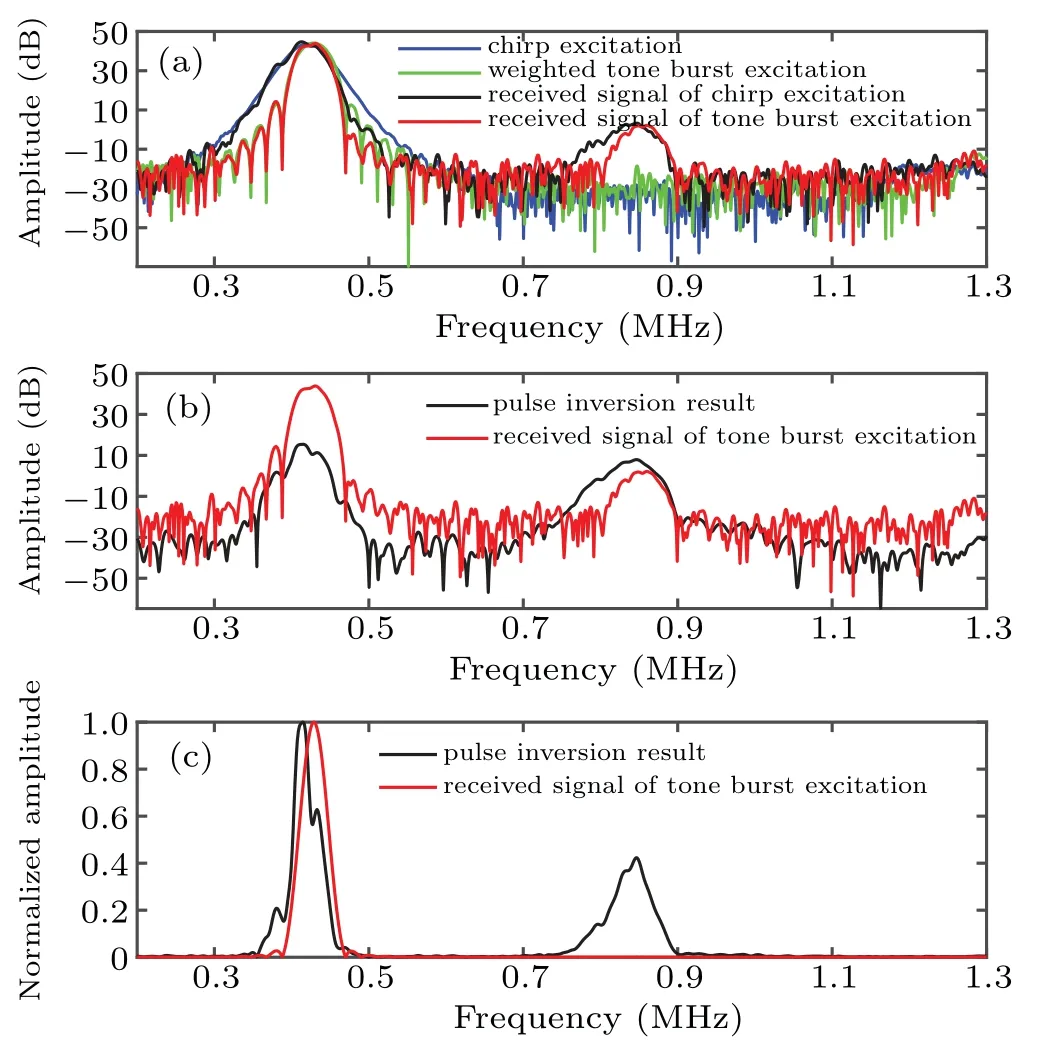
Fig.8.The spectra of excitation and received signals after fatigue loading:(a)spectrum of excitation and received signals,(b)spectrum of pulse inversion and tone burst excitation results,and(c)normalized amplitude spectrum.
Therefore,the pulse inversion is chosen as the decoding approach for subsequent experiments.
4.3.Bone fatigue evaluation
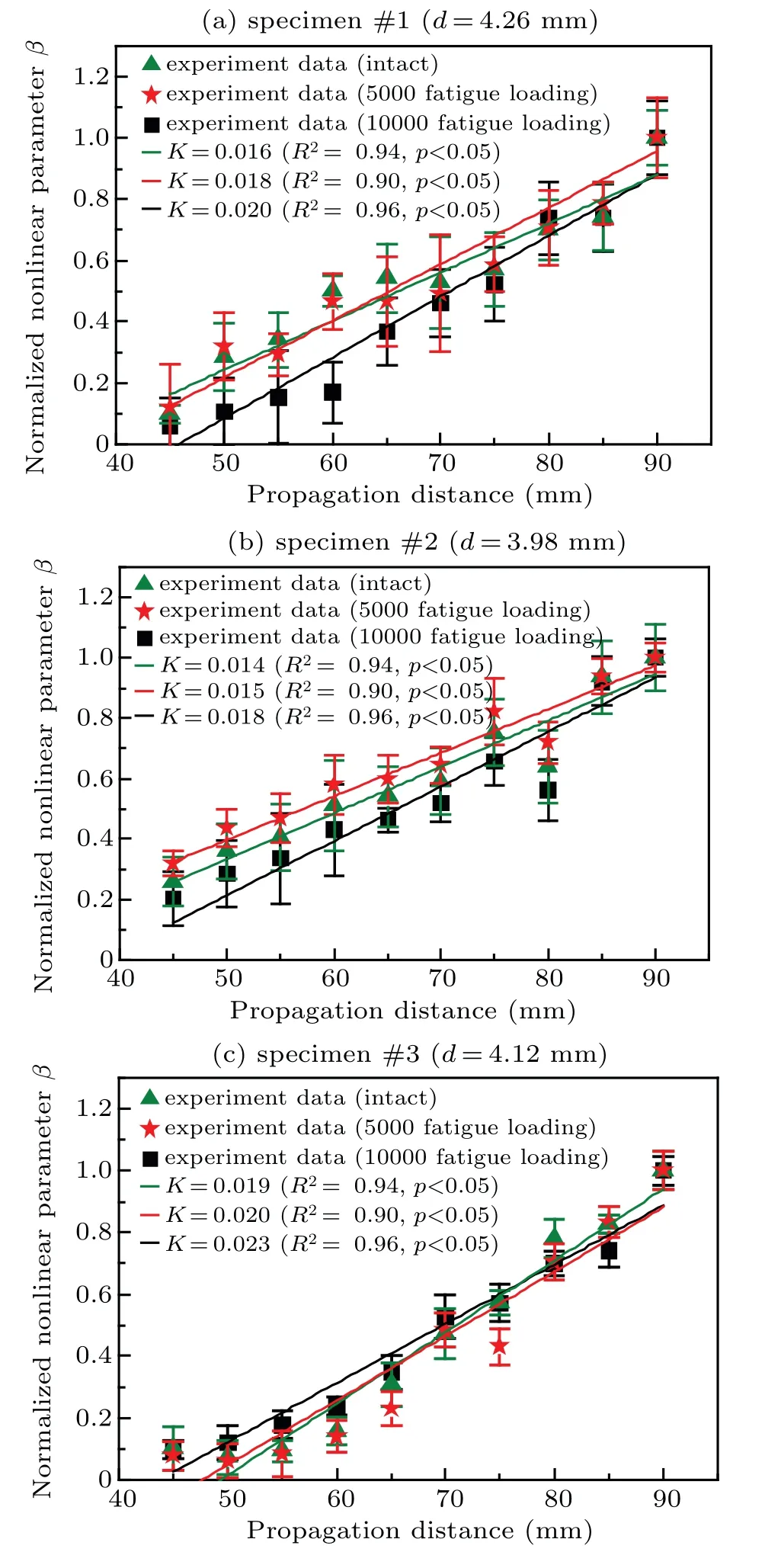
Fig.9.The fitting curves of nonlinear parameter and propagation distance:(a)specimen#1,(b)specimen#2,and(c)specimen#3.
The nonlinear parameters of the three fatigue levels show a trend of linear growth with the propagation distance,which is because the elastic modulus and other parameters of the bone plate have not changed too much while being stretched.With the dispersion curve changes slightly,the cumulative harmonic conditions are still satisfied at the same excitation frequency.In the experiments of three specimens,the excitation frequency and bandwidth are set as 0.42 MHz and 0.1 MHz respectively.The correlation coefficient and the slope of the fitting curves of these three specimens are summarized in the following Table 2.
As Table 2 shows,the slope of nonlinear parameters with propagation distance k is the smallest when the bone plates have not been stretched;when the number of fatigue loading times reached 5000,the slope k had an average increase of 8%,compared to the case of intact bone;when the loading times reached 104,the average increase of slope is 24.9%.

Table 2.Experiment parameters and results of three specimens.
5.Discussion
The nonlinear ultrasound technique has the advantage of being sensitive to micro-cracks in material.[13,14]The utilization of nonlinear ultrasound can be expanded to bone fatigue evaluation since the existence of nonlinear ultrasonic response was proved when the microdamage in bone is accumulating.[33]
As a medium with irregular internal structure,bone has a large absorption and scattering effect on ultrasound,making the signal extremely weak.Although researches on nonlinear ultrasonic measurement have been carried out on bones,it is difficult to extract the second harmonic amplitude due to the defects of anisotropy,rough surface,and noise.
The method of applying the pulse inversion to the chirp excitation to extract the second harmonic component plays an important role in the work.Pulse inversion,as a special filtering method,is often used in harmonic imaging.The spectral overlap between fundamental and second harmonic signal content is common for harmonic imaging.[53]Although bandpass filtering is the most commonly used method to extract the second harmonic,it is still a challenge to filter out the fundamental component because of the spectral overlap.However,pulse inversion has the advantage to extract the second harmonic without bringing in the range sidelobe artifact.More importantly,the migration of the method from harmonic imaging to Lamb waves second harmonic detection can break the limitation of imaging frame rate,since the pulse inversion requires two transmissions.The detection of second harmonic generation is a one-time process,there is no requirement for imaging frame rate,nor the penetration and axial resolution.
In terms of cumulative second harmonic generation conditions,excitation with chirp rather than single frequency tone burst eliminates the need to find the best phase-matching frequency point.Once the approximate excitation frequency is figured out,the corresponding chirp excitation can be settled.It provides the possibility of in vivo nonlinear ultrasound detection.The skeletal properties(such as cortical thickness,elastic modulus)vary in people of different ages,so for the cumulative second harmonics,the excitation frequency fluctuates over a range rather than a fixed value.
The results of applying pulse inversion of chirp signals to nonlinear ultrasound detection are also promising.From the spectral analysis,the amplitude of the second harmonic is doubled after pulse inversion,which can be inferred from Eqs.(7a)and(7b).Theoretically,the fundamental frequency component will be eliminated after pulse inversion,but in the actual experiment,the fundamental frequency is two orders of magnitude higher than the second-harmonic amplitude,which makes the suppression not so ideal.
In summarization of the chirp-coded excitation part,the chirp coding and pulse compression method significantly improve the amplitude of the second harmonic,which is also equivalent to improving the SNR of the second harmonic.
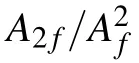
There are also some limitations in this work.Although a fatigue loading experiment was conducted to simulate the microdamage or degradation in bone,the level of microdamage accumulation was not assessed quantitatively.The measurement of the second harmonic Lamb wave was limited to a regular and isotropic plate-like sample,while most of the bones are anisotropic and have an irregular shape.More practical simulation models and experiments should be explored in future studies.
6.Conclusion
In this study,the nonlinearity of the cortical bone plates before and after fatigue loadings were observed and compared using an encoding and nonlinear ultrasound.The main findings of this article are as follows.Firstly,the chirp signal application in nonlinear ultrasound detection could ensure cumulative second harmonic generation while eliminating the step of finding the optimal frequency point.Secondly,the coding and pulse inversion method applied to the nonlinear ultrasonic measurement could improve the measurement accuracy.Thirdly,there is a significantly positive correlation between the in vitro bone fatigue level and the growth rate of the second harmonic amplitude with propagation distance,as well as the relative nonlinear parameter.The coded nonlinear ultrasound measurement method might become an early evaluate tool for bone progressive process of microdamage deteriorating under long-term and repeated stress.
- Chinese Physics B的其它文章
- Origin of anomalous enhancement of the absorption coefficient in a PN junction∗
- Protection of isolated and active regions in AlGaN/GaN HEMTs using selective laser annealing∗
- First-principles study of plasmons in doped graphene nanostructures∗
- Probing thermal properties of vanadium dioxide thin films by time-domain thermoreflectance without metal film∗
- An improved model of damage depth of shock-melted metal in microspall under triangular wave loading∗
- Signal-to-noise ratio of Raman signal measured by multichannel detectors∗

