力学压轴题的多解分析及教学启示——以2016年高考全国Ⅰ卷第25题为例

力学压轴题的多解分析及教学启示
——以2016年高考全国Ⅰ卷第25题为例

陈 翠 肖 洋 熊建文

对2016年高考全国Ⅰ卷物理第25题中弹性势能的求解进行了详细分析并给出了多种解法，突出了物理过程模型在解决物理问题中的重要作用．提出一线教师应注重模型教学，让学生透彻理解物理概念，学会分析物理情境以正确建立物理过程模型，从而减轻学生认知负担，促进自主学习．

2016高考 物理过程模型 建模教学

2016年高考全国理综Ⅰ卷物理试题充分体现了以主干知识与核心概念为载体[1]，紧密联系由课程标准和教材转向课堂教学的课改焦点[2]，着重考査了学生的物理学科素养，尤其注重考查学生的综合分析和解决物理问题能力．其中，第25题作为力学综合压轴题，将斜面、弹簧及圆弧轨道等传统实物材料[2]进行组合并创设出新的物理情境，在体现物理与科学、生活及社会密切联系的同时，凸显了物理过程模型在解决实际问题中的应用．

物理过程模型是指在物体运动变化过程中根据研究问题的性质和需要，在包含多种复杂因素的物理过程中抓住主要因素、忽略次要因素而建立的能够揭示事物本质的理想过程[3]．其作为物理学的核心内容，充分体现物理科学核心素养，学生经历物理模型的建构过程，可获得对知识深刻而全面的理解并发展自己的模型建构能力[4]．2014年全国卷、2015年全国卷和2016年上海卷的力学压轴题分别以刹车情境、碰撞和风洞实验为载体考查了匀变速直线运动、平抛运动和自由落体运动等重要物理过程模型，2016年全国卷又深入考查了匀变速直线运动和平抛运动，可见能充分反映物理核心知识点的物理过程模型在教学中已愈显重要．因此，能否有效地理解命题者所建立的模型是正确解题的关键．基于利用模型研究物理问题的建模教学已成为一线教师进行课堂教学创新的入手点，对高中物理教学具有良好的导向作用．

下面将从不同思维分析过程出发，对2016年全国Ⅰ卷第25题第(2)问进行详细剖析，突出物理过程模型在求解弹簧弹性势能的重要作用，希望对一线教学有一定的启示．

1 试题呈现

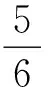
(1)求P第一次运动到B点时速度的大小；

(2)求P运动到E点时弹簧的弹性势能；

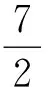
图1 原图

2 试题解析

弹簧是中学物理中常见的研究对象，弹簧问题往往与高中物理的核心规律——牛顿运动定理、能量的转化与守恒规律以及弹力规律密切相关，从而成为高中物理教学的重点[5]．

第(2)问首先考查学生对常见的临界状态——弹性势能最大位置的判断，更重要的是考察学生选取过程模型的能力．求解物块P运动到E点(弹簧的压缩量达到最大)时弹簧的弹性势能的大小，首先明晰P沿斜面下滑并压缩弹簧至最低点的“下滑过程”与弹簧回复时物块P沿斜面向上运动的“上滑过程”中经过的位置关键点，进而明确这些关键点的特点和所处状态，构建合适的物理过程模型，最后利用动能定理进行求解．

物块P由C点沿斜面静止释放的“下滑过程”中，先经过F点后到达B点，再压缩弹簧使其压缩量最大时至E点；再由E点被弹回的“上滑过程”中先经过B点，最高至F点．在下滑和上滑的两个过程中，位置关键点分别是：C，F，B，E点．选择不同的起点和终点，构建4种物理过程模型．每种模型最终可整合为物块运功路径的“全过程”、“下滑过程”和“上滑过程”，详细物理过程模型分类如图2所示．

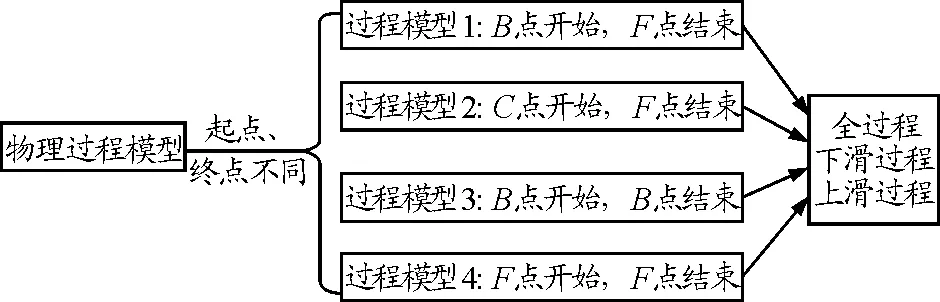
图2 物理过程模型分类

下面将对各个过程模型进行详细论述．

2.1 过程模型1：B点开始，F点结束

承接第(1)问，按物理过程发生的顺序建构过程模型1．

物块P以速度vB从B点开始压缩弹簧至E点达到其最大压缩量(设BE=x)的下滑过程中，重力做正功，弹力和摩擦力做负功，弹性势能增加；随后弹簧回复原长，P由E点到达B点的上滑过程中，弹力做正功，弹性势能减小，摩擦力和重力做负功；当弹簧回复原长后，P再沿轨道由B点向上运动到最高点F，摩擦力和重力继续做负功．而P在由B点至E点，再由E点至F点的全过程中，弹力做功之和为零．

由几何关系知

BF=AF-AB=2R

解法1：下滑过程(BE段)和上滑过程(EF段)，利用动能定理，得

下滑过程

mgxsin 37°-μmgxcos 37°-Ep=

(1)

上滑过程

Ep-mg(x+2R)sin 37°-

μmg(x+2R)cos 37°=0

(2)

已知

联立式(1)、(2)，解得

x=R

解法2：全过程，利用动能定理

-mg2Rsin 37°-(2x+2R)μmgcos 37°=

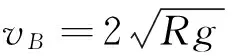
2.2 过程模型2：C点开始，F点结束

由于物块P从C点沿斜面静止下滑接触弹簧后最终上滑至最高F点，在这两点的动能均为零，可将第(1)问求解的速度vB作为中间量不参与运算来建立过程模型2．

P由从C点至E点的下滑过程中，重力做正功，弹力和摩擦力做负功，弹性势能增加；由E点至F点

的上滑过程分析与过程模型1的分析相同；全过程中，弹力做功之和为零．

解法1：下滑过程(CE段)和上滑过程(EF段)，利用动能定理，得

下滑过程

mg(x+5R)sin 37°-

μmg(x+5R)cos 37°-Ep=0

(3)

联立式(2)、(3)，解得

同时，将过程模型1中的解法2解得的x=R代入式(3)也可得

解法2：全过程，利用动能定理

mg(7R-4R)sin 37°-

μmg(7R+2x)cos 37°=0

(4)

直接解得x=R，将其分别代入式(1)或(2)或(3)，均解得

也可选取物块在下滑过程和上升过程经过的同一点——B点或F点为研究起点和终点，对物体在斜面运动的过程采用对称的物理思想来分析．

2.3 过程模型3：B点开始，B点结束

B点恰好是物块P接触和离开弹簧的位置，均具有速度，而此时弹簧正好处于原长状态，其Ep=0．抓住B点，对其深入研究来建立过程模型3．

P由B点至E点的下滑过程与E点至B点的上滑过程的分析与过程模型1相同．而在全过程中，弹力、重力做功之和均为零．

此时，分两步求解．

第一步：求P在上滑过程中经过B点的速度vB2．

P在合外力(受力分析示意图如图3所示)的作用下，以初速度vB2由B点沿斜面匀减速直线至F点，位移BF=AF-AB=2R．

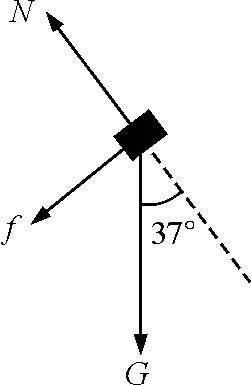
图3 上滑时P的受力分析示意图

P由B点运动到F点，由动能定理得

(-mgsin 37°-μmgcos 37°)×2R=

解得

第二步：求解Ep．

解法1:下滑过程(BE段)和上滑过程(EB段)，利用动能定理，得

上滑过程：

Ep-mgxsin 37°-μmgxcos 37°=

(5)

联立式(1)、(5)，解得

x=R

解法2:全过程，利用动能定理

解得x=R，将其分别代入式(1)或(5)，解得

2.4 过程模型4：F点开始，F点结束

F点是物块P在上滑过程中被弹至斜面的最高点，在下滑过程中P在该点获得速度vF．抓住F点，建立过程模型4．

P由F点至E点的下滑过程中，重力做正功，弹力和摩擦力做负功，弹性势能增加；P由从E点至F点的上升过程的分析与过程模型2相同；在全过程中，重力、弹力做功之和均为零．

同样，分两步求解．

第一步：求P在下滑过程中在F点速度vF．

P在合外力(受力分析示意图如图4所示)作用下，由C点静止沿斜面匀加速下滑运动到F点，位移CF=AC-AF=3R．

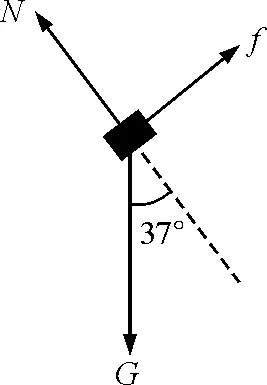
图4 上滑时P的受力分析示意图

物块P由B点运动到F点，由动能定理得

可得

第二步：求解Ep．

解法1:下滑过程(FE段)和上滑过程(EF段)，利用动能定理，得

下滑过程

mg(x+2R)sin 37°-

(6)

联立式(2)、(6)，解得

解法2:全过程，利用动能定理

直接解得

x=R

将x=R分别代入式(2)或(6)，解得

小结：在4个过程模型中，选取全过程可直接求得最大压缩量x=R．因为在全过程中弹力做功之和为零，只需分析重力、摩擦力做功情况及动能的变化量，做到化繁为简，最后利用动能定理可直接求解x．再结合在该模型中的下滑过程或上滑过程，即可解得Ep．

利用过程模型3和过程模型4时，需计算物块在上滑过程经过B点及在下滑过程经过F点的速度大小，虽然在一定程度上增加了计算量，但利用对称思想建立过程模型抓住某一位置点，对其深入研究，可使研究过程明了．同时，选取具有特殊物理特点的始末态，剖析问题的物理本质，使物理问题的解决更简捷．

可设AE=x，CE=x，EF=x(x并非弹簧的最大压缩量)，利用以上方法求解Ep．

3 教学启示

基于建构主义的建模教学为改变学习者头脑中的错误概念进而形成科学概念提供了有利的工具[6]，其有助于矫正传统教学方法中的知识的零碎性和学生的被动性的教学效果已得到很多研究的证实[4]，是当前“科学探究”教学不可或缺的能力[7]．

建模教学应帮助学生学会从复杂的物理情境中抽取出能描绘该情境的物理量，并找出这些物理量之间的正确联系，建构足以正确描述、解释该情境的物理过程模型，促使学生头脑中形成一种优化的知识表征方式[8]，能使学习者在面对新问题情境时调用已有概念域中的相关概念成功解决物理问题[9]．在平时教与学的过程中，师生应该重视从同一角度、同一层次、同一途径分析不同的物理问题，重视从多侧面、多层次、多途径分析同一物理问题[10]，注意领会建立物理模型的思路和方法，使其成为学生知识新的增长点，帮助学生学会自我生长．同时，教师在协助或引导学生建立模型时，可以将模型分成数个较小模块，一方面帮助自己设计教学内容和评价教学效果；另一方面让学生先学习过程模型中的小模块，减轻学生认知负担；最后再将各个小模块的知识整合并发展出合适、有意义的模型，促进学生自主学习．

教师在利用建模教学对学生进行一题多解的发散思维训练时应使学生灵活掌握物理知识的纵横联系，注意培养学生思维的深刻性及综合性．同时，应将该训练尽量安排在学习某一章节或某模块知识内容后，有利于学生对这部分知识的深层次的理解和掌握．

1 陈汉光.2016年高考全国理综Ⅰ卷物理试题评析及对教学的启示.物理教学,2016(9):61～64

2 张恩德.近10年我国高考物理压轴题的命题特点及其启示.物理教师,2015,36(2):75～83,86

3 郑艳秋.高中理科学生物理建模能力的评价研究：[硕士学位论文].广州：华南师范大学,2007

4 张静,郭玉英.物理建模教学的理论与实践简介.大学物理,2013(2):25～30

5 叶正勇.谈弹簧的弹力和弹性势能.物理教师,2015,36(1):55～59

6 周红,马云鹏,张二庆.模型与建模在科学教育概念转变中的作用及启示.现代教育管理,2013(4):52～55

7 王全,母小勇.模型与建模:国际物理教育新视点.外国中小学教育,2009(3):55～58

8 吴国华.提高学生建立物理过程模型的能力打造高效课堂教学.中学物理:初中版,2010(8):22～23

9 翟小铭,郭玉英.科学建模能力评述:内涵、模型及测评.教育学报,2015(6):75～82

10付艳明.分析高考物理试题以提高学生物理建模能力的教学实践：[硕士学位论文].呼和浩特：内蒙古师范大学,2015

�学物理与电信工程学院 广东 广州 510006) (

2017-03-14)