双电荷在匀强磁场中的运动轨迹①*

杨 洁

(湖州师范学院理学院 浙江 湖州 313000)

姜付锦

(武汉市黄陂一中 湖北 武汉 430300)

邱为钢

(湖州师范学院物理视觉工作室 浙江 湖州 313000)

双电荷在匀强磁场中的运动轨迹①*

杨 洁

(湖州师范学院理学院 浙江 湖州 313000)

姜付锦

(武汉市黄陂一中 湖北 武汉 430300)

邱为钢

(湖州师范学院物理视觉工作室 浙江 湖州 313000)

给出了质量和电荷值相等的双电荷在匀强磁场中的运动方程，讨论了运动守恒量和轨迹特性；数值求解方程，给出了轨迹封闭时轨迹曲线．

双电荷 匀强磁场 轨迹

点电荷在匀强电场和磁场中运动，随着初始条件的不同，轨迹可以为抛物线、螺旋线、摆线等[1，2]；作为推广，我们考虑点电荷产生的电场和匀强磁场复合电磁场中点电荷的轨迹问题，分为三种模型．三种模型都是在起始时刻加上一个匀强磁场, 磁场垂直于点电荷运动平面. 第一种模型是一个负电荷固定，一个正电荷做匀速圆周运动，加上匀强磁场后正电荷的运动轨迹；第二个模型是自由异号双电荷，起始静止，在匀强磁场中的运动轨迹；第三个是自由同号双电荷，起始静止，在匀强磁场中的运动轨迹．

1 第一种模型对应的电荷运动轨迹

设固定电荷电荷量为-q，运动电荷为+q，质量为m，原先绕固定电荷做匀速圆周运动，半径是L．以加入匀强磁场时刻记时，以固定电荷为原点，设运动电荷的位移为r，那么运动方程是

(1)

无论为了解析分析还是数值计算方便，要把以上方程量纲归一化．设长度量纲是L，时间量纲是T0，磁场量纲是B0．式(1)中的3项量纲相等，都是力的量纲，得到

(2)

由此得到

采用极坐标，设磁场强度为B=kB0ez，其中k是磁场相对强度，即磁场强度与磁场量纲B0的比值．运动电荷位移为r=ρeρ.

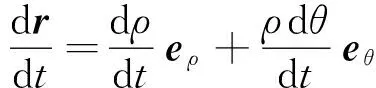
(3)

把以上各式代入式(1)，得到量纲归一化后的运动方程

(4)

(5)

(6)

(7)

这个守恒量其实就是量纲归一化后的能量．式(6)中解出角速度的表达式，然后代入式(7)，化简得到

(8)

利用数学软件分析发现，式(8)右边有两个实根，一个是ρ=1，还有一个就是矢径极值．电荷从矢径为1的地方运动到矢径极值处，然后继续运动到矢径为1的地方，形成一个运动周期，这也为数值计算结果所验证．但是周期转动角不再是2π的有理数倍，一般不会返回到原处．

我们用数值求解式(4)和式(5)的方法来求轨迹．数值计算给出，当磁场相对强度k取适当值时，周期转动角是2π的有理数倍，电荷的运动轨迹封闭且有对称性．磁场正方向时，对称封闭轨迹如图1所示.

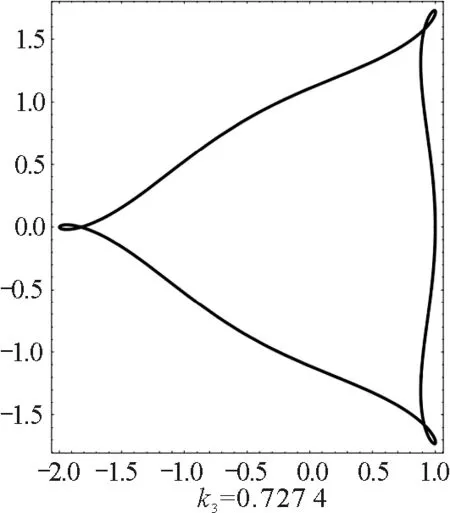
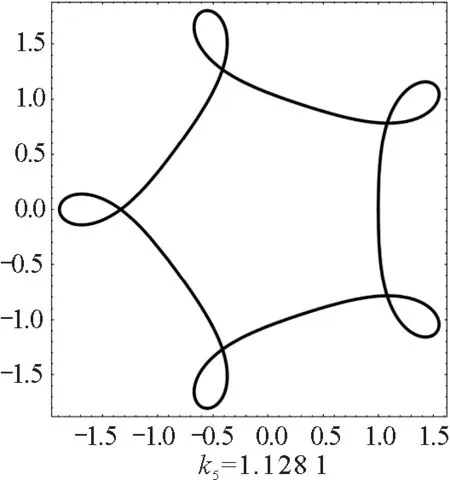
图1 磁场正方向时正电荷的对称封闭轨迹

磁场反方向时，对称封闭轨迹如图2所示.

图2 磁场反方向时正电荷的对称封闭轨迹

2 第二种模型对应的电荷运动轨迹

设起始时候正电荷在坐标(1,0)处，负电荷在(-1,0)处，两个电荷起始速度都为零．设正电荷的坐标是(x1,y1)，负电荷的坐标是(x2,y2)．由对称性可知

x1(t)=-x2(t)=x(t)

y1(t)=y2(t)=y(t)

那么两个电荷的量纲归一化后的4个运动方程简化为以下两个方程

(9)

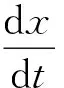
(10)

(11)

那么右边正电荷在(xmin,1)区间做周期运动．

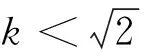
当磁场相对强度k分别等于0.6,0.9,1.2时，两个电荷的运动轨迹如图3所示.

图3 小于临界值时不同相对强度磁场下的异号双电荷轨迹

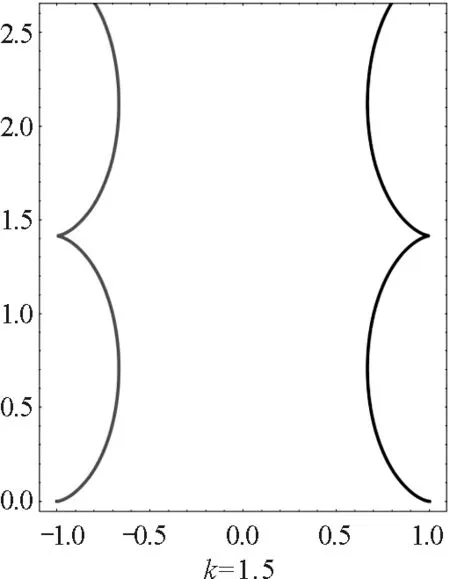
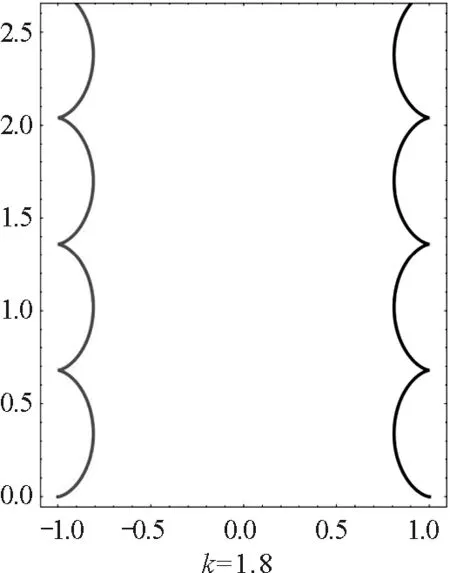
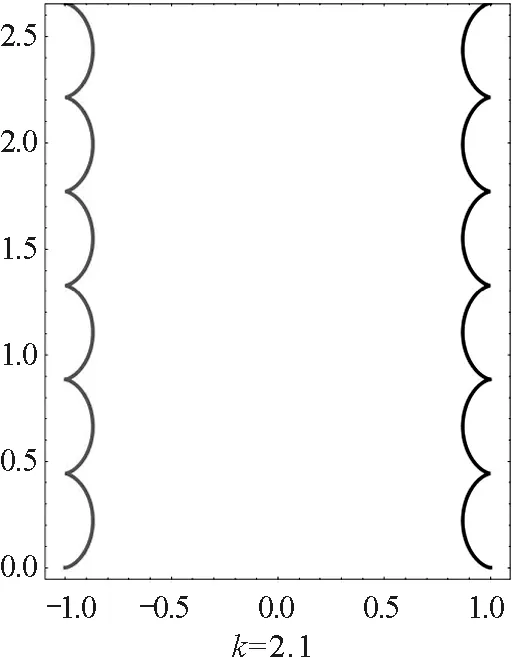
图4 大于临界值时不同相对强度磁场下 异号双电荷周期运动轨迹

3 第三种模型对应的电荷运动轨迹

设起始时候一个正电荷在坐标(1,0)处，另一个正电荷在(-1,0)处．采用极坐标，由对称性，两个电荷的坐标分别是(ρ,θ)和(ρ,θ+π)．仿照第一种情况的推导，得到量纲归一化后的运动方程

(12)

(13)

由对称性，磁场正方向和反方向的轨迹一样，只是运动方向相反，所以我们只考虑正方向的磁场．数值求解式(12)和式(13)，当磁场相对强度k取适当值时，周期转动角是2π的有理数倍，电荷的运动轨迹会封闭且有对称性，如图5所示.

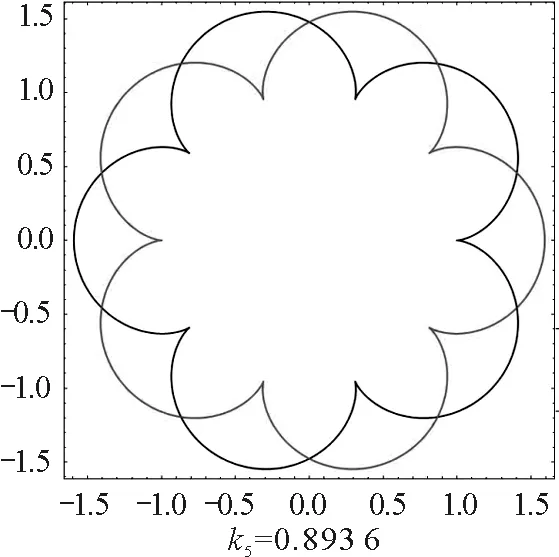
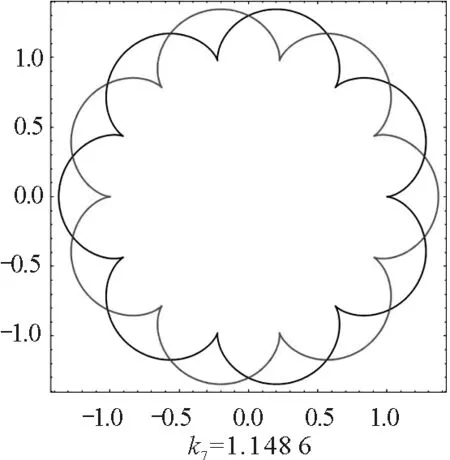
图5 不同相对强度磁场下同号双电荷周期运动轨迹

4 结束语

通过数值求解双电荷在匀强磁场中的运动方程，发现绕固定电荷运动的电荷轨迹具有周期性，磁场相对强度取适当值时，轨迹具有封闭对称性；自由异号双电荷存在一个临界磁场，小于这个临界值，它们会相遇；大于这个临界值，它们会做对称的周期运动．自由同号双电荷则做对称的周期运动，当磁场相对强度取适当值时，轨迹具有封闭对称性．以上3种轨迹，推广了文献中电荷运动轨迹，给物理中的运动轨迹曲线宝库增加了新成员．

1 汪静谊．电子在相互垂直的电场和磁场中运动轨迹的讨论.大学物理，1988，7(9)：43～45

2 佘守宪，唐莹．重力场和正交均匀电磁场中的旋轮线(摆线).物理与工程，2001，11(6)：12～18

TheMotionTrajectoryofDoubleChargeintheUniformMagneticFields

YangJie

(SchoolofScience,HuZhouTeachersCollege,HuZhou,ZheJiang313000)

JiangFujin

(TheFirstHighSchoolofHuangpiDistrictinWuhan,Wuhan,Hubei430300)

QiuWeigang

(PhysicsVisualStudio,HuZhouTeachersCollege,HuZhou,ZheJiang313000)

The equations of motion of double-charge in the uniform magnetic field are given. The constants of motion and the characteristics of orbits are discussed. The closed symmetric orbits are drawn from the numerical solution.

double charge;uniform magnetic field;orbit

*高等学校力学课程教学研究项目，编号：JZW-15-LX-15；湖州师范学院教改项目，编号：JGB16022；浙江省高校物理教学研究项目，编号：w201709；国家自然科学基金，编号：11475062

杨洁 (1996- ),女，在读本科生.

2017-02-02)

①《物理通报》湖州工作室、武汉工作室供稿.