分数阻值的电阻化简问题*
陈 胤
(南京市第十八中学 江苏 南京 210022)
分数阻值的电阻化简问题*
陈 胤
(南京市第十八中学 江苏 南京 210022)

电阻 化简 定量分析 电学
1 引言
问题来源于这样的习题:电阻R=10 Ω,现有5 Ω的电阻若干:
(1)怎样才能使电路中的电流增大到原来的两倍?
(2)怎样才能使电路中的电流缩小到原来的0.5倍?

mn个电阻组成一个mn方阵,如图1所示.

图1 mn方阵
这个方阵中用的电阻有mn个之多,显然太多了,我们希望使用的电阻当然是越少越好.但是,怎样去化简呢?
2 问题讨论


这个引理的证明非常简单,方法见引言,此处略过.但是却是我们化简的基础,它告诉我们,在我们组成的mm电阻方阵中,就可以被一个电阻替代.
3 化简方法

如果m>1,在这个mn方阵中一定有mm方阵,它有多少个呢?
由于
mn=k1mm+q1m (1≤q1 (1) 所以这之中的有k1个mm方阵,它们可由k1电阻替代,如图2所示. 图2 k1个mn方阵,可由k1个电阻替代 在剩余下的q1m的电阻方阵中,又有 q1m=k2q1q1+q2q1(1≤q2 (2) 这之中的有k2个q1q1方阵,它们可由k2电个阻替代,如图3所示. 图3 k2个q1q2方阵,可由k2个电阻替代 反复(1)和(2)的步骤,最后 qjqj-1=kj+1qjqj+qj+1×qj=kj+1qjqj (qj=1,qj+1=0) (3) 实际上只剩下kj+1个电阻,注意到qj=1,是整个简化过程结束的标志. 我们将简化的过程归纳为:逢方归一,横向并接,纵向串接,遇一结束. 我们来看一个例子. 图4 4×15的电阻方阵 现在我们来化简,请看 (1)首先在图4左边可以得到3个4×4的电阻方阵,可以简化成3个横向的电阻,如图5所示. 图5 图4左边3个4×4电阻方阵,可简化为3个横向电阻 (2)右上角又可以得到1个3×3的电阻方阵,再简化成1个纵向的电阻,最后右下角是1个1×3的方阵,不可以简化了,就放3个横向的电阻,按照横向并接,纵向串接,简化后的结果连接起来,如图6所示.总共用了7个电阻. 图6 简化结果 (1)说明:从式(1)~(3)可以得到 n=k1m+q1(1≤q1≤m) (1′) m=k2q1+q2(1≤q2≤q1) (2′) ………… qj-1=kj+1qj+qj+1=kj+1qj+0 (qj=1,qj+1=0) (3′) 式(1′)、(2′)…及 (3′)实际上就是求m和n的最大公约数(m,n)的辗转相除法,因为(m,n)=1,所以qj=1. (2)设在前面分数电阻化简的整个过程中,我们最后一共用了k个电阻,按照我们前面的阐述有 k=k1+k2+…+kj+1 (4) 而从式(1′)得到 n=k1m+q1≥k1m+1≥k1+m 从式(2′)…(3′)可以得到类推得到 m≥k2+q1 q1≥k3+q2 ………… 根据式(4),所以有 n≥k1+k2+…+kj+1 (5) (4)当m和n不互素,即(m,n)=d>1时,可以先约分至互素,再用上面的方法. 还可以先按照上面的方法做,到出现 下式的时候结束.两种方法结果完全相同. qjqj-1=kj+1qjqj+qj+1×qj= kj+1qjqj=kj+1dd qj+1=0 初中物理中的一些问题,如果深究下去,其实是很有意思.探究的同时,也能提高物理教师本身的素质. Highlights:Given mn value of resistance of 1, it can form a resistor whose value is a fractional resistance--n/m. This essay gives a method to simplify it using the least number of resistors but the resistance is still the same. TheResistanceReductionIssueofFractionalResistance ChenYin (No.18HighSchoolNanjing,Nanjing,Jiangsu210022) electric resistance;simplify;quantitative analysis;electrics *系南京市教育科学“十二五”规划2015年度课题“中学物理课程资源开发与学生科学探究能力培养研究”,中国教育学会物理教学专业委员会2013-2016年全国物理教育科研重点课题“中学物理实验研究”之阶段性研究成果. 2017-02-22)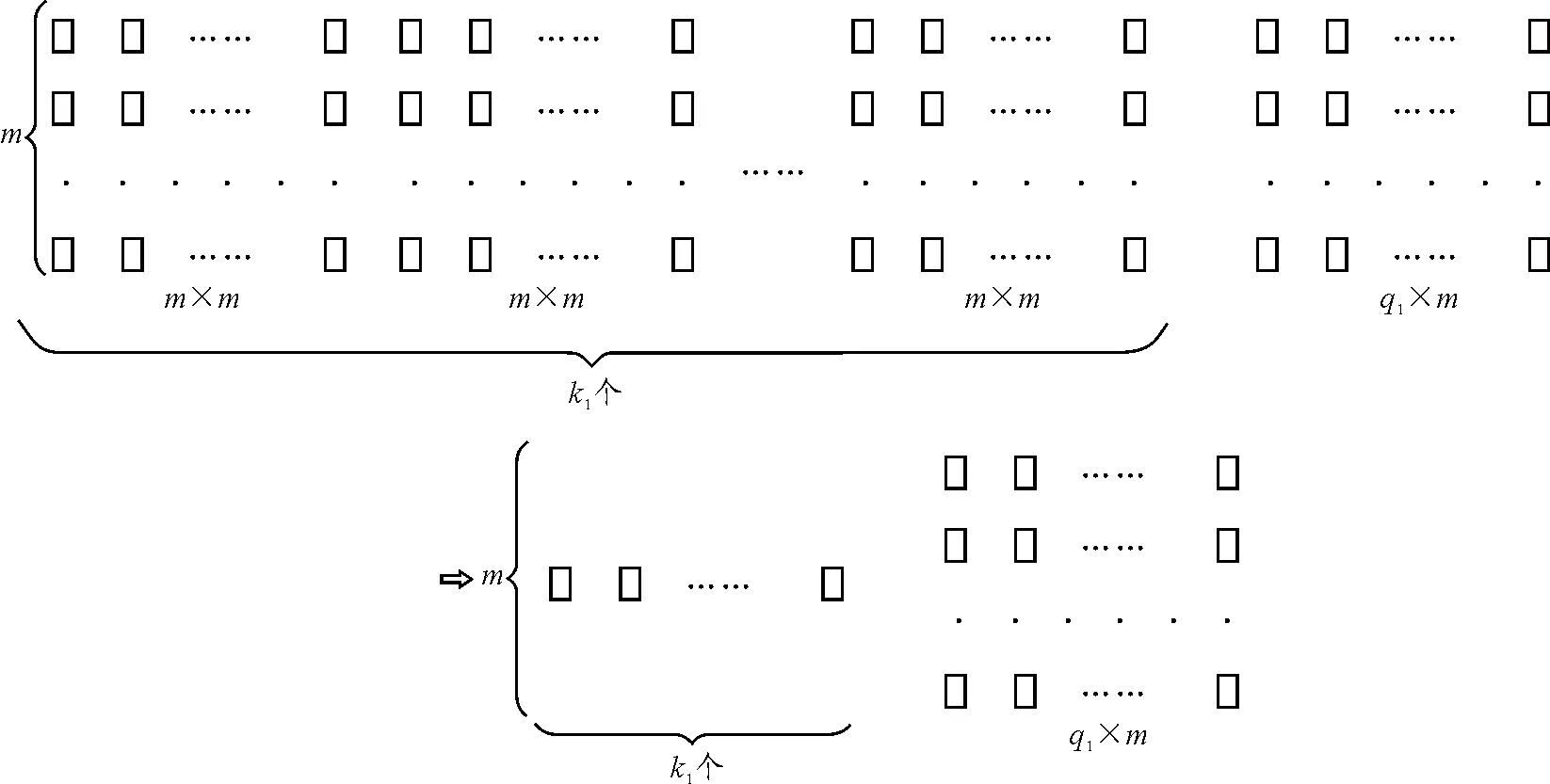

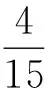



4 讨论

5 结束语

