基于Lingo的关键路径法在冷链物流中的应用

曹 茜，宋筱影 （上海电力学院，上海 201399）

·现代物流·

基于Lingo的关键路径法在冷链物流中的应用

曹 茜，宋筱影 （上海电力学院，上海 201399）

冷链物流是近期发展起来的新型物流形式，物流企业在进行冷链配送时往往会进行多方面的考虑。文章主要研究了关键路径法在冷链物流中的应用，通过分析具体的实例，并运用Lingo软件进行求解来解决关于冷链物流中配送的时效性问题。

关键路径法；冷链物流；Lingo

0 引言

关键路径法（Critical Path Method，CPM）[1]作为目前现代项目管理的重要管理工具，是通过分析某项活动过程中各子项进度安排的最少时差之和，以此来对该活动的时间和成本进行预测和优化的方法。

关键路径法作为一种网络技术中的重要方法，在物流行业有着许多的应用。而在整个物流过程中，物流的配送是其中非常重要的一个环节。它是公司根据不同企业不同的要求，对其需要的产品进行分拣、包装以及配货的过程。物流配送的时效性对于客户满意度和企业的日常经营具有较大的影响，而在冷链物流的配送中，这种影响则会更为重要。

1 关键路径法

关键路径法简单来说就是对一个大型的项目进行分解，然后根据估算的各个任务的时间及其活动之间的相互联系建立起关联关系，形成一个网络，通过对建立起的网络模型求解，就可以找到网络图中的关键路径，可通过它追踪整个计划实施的进度，对关键路径上的活动进行有效的控制与调整，最后制定出一个最优的方案。

关键路径法的操作步骤大致如下：

（1）列出组成项目的活动清单。每个项目都可分解为一个个小的活动和步骤，正是这些活动按照一定的顺序连接起来才形成了整个项目。

（2）确定每项活动的紧前活动。紧前活动即是紧挨着该项活动前面的事件。也可理解为，只有当紧前活动结束时，该项活动才能开展。

（3）估计每项活动的完成时间。

（4）绘制网络图。根据活动清单和每项活动的紧前活动来绘制图形。流程方向用箭头来表明，箭头上方标注每项活动的完成时间，节点以圆圈表明，代表事件。

（5）建模求解。关键路径模型是一个相对成熟的模型，运用许多软件都可以用它进行求解，例如WINQSB、Microsoft Office Project、Matlab、Lingo软件等。本文主要讨论用Lingo软件进行建模求解的方法。

（6）找出整个项目的关键路径。

2 冷链物流

冷链物流是国民经济中的一项重要经济活动[2]，指生鲜冷冻食品等需要在低温环境下进行储存、运输和配送的一项工程。因为其对稳定的温度要求较高，所以与其他常温的物流配送相比，难度和成本也要更高。是否能进行准时的冷链物流配送，满足物流时效的要求，直接关系到物流企业的经济效益。

在配送问题中应用关键路径法，主要应用到了关键路径是整个项目中持续时间最长的路径这一特点。可以将物流配送过程中的连接弧抽象为活动，即将一地到另一地的运输过程看成是一个活动，连接弧上的数字，即两个地点之间货物的运送时间看做为该活动执行所需要的时间。所以，就可以根据这个配送模型建立一个计划网络图，在这个计划网络图中，路径最长也就是配送时间最长的路径就是关键路径。若是关键路径的长度满足了配送时效的要求，那么该企业就可以进行及时的物流配送。

3 建立模型

近年来，由于人们对生鲜冷冻食品等的需求，冷链物流成为了现代物流发展的重点。V1企业是一家冷链物流配送企业，位于图1中①所示位置， V10企业是一家快餐店，位于图1中⑩所示位置。V1企业到V10企业的连通路径如图1所示，连接弧上的数字表示两个节点之间货物的运送时间。现在V1企业承担了为V10企业运输冷冻食品的任务，由于货物的特殊性，V10企业提出V1企业必须在12个小时内将货物送达，否则车厢里的冷冻食品就会变质。在最坏的情况下，V1企业能否为V10企业进行及时的物流派送是本文要解决的问题。

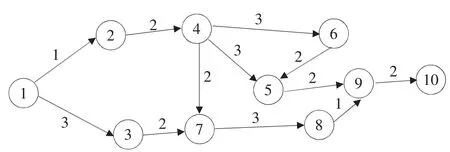
图1 连通路径及时间

4 利用关键路径法求解

本文将求出这个网络的关键路径，并计算其长度。若是关键路径的长度小于规定配送的时间，则说明就算是在最坏的情况下，V1企业也能为V10企业进行及时的物流派送；否则，V1企业就不能为V10企业进行及时的物流派送。

（1）建立计划网络图

首先，根据图1建立货物物流配送作业的数据表（表1）及计划网络图（图2）。

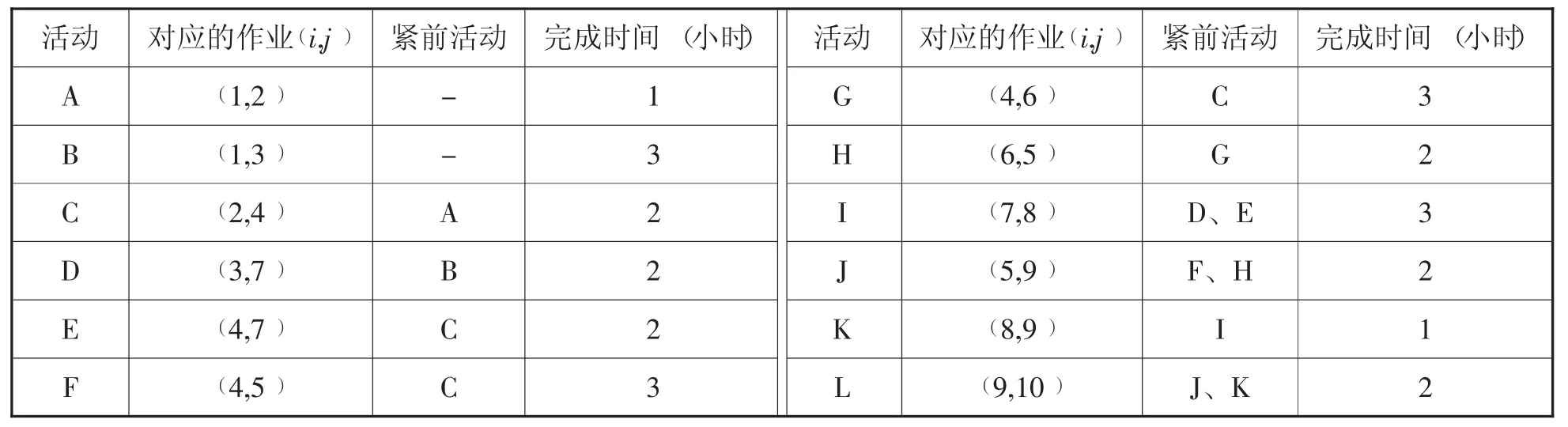
表1 货物物流配送作业数据

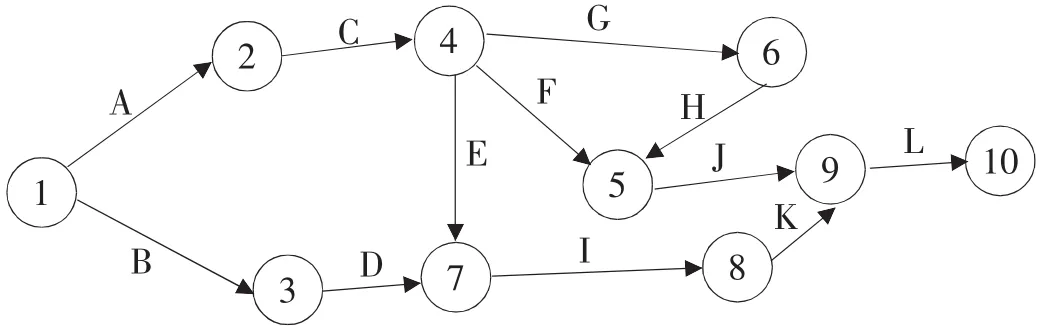
图2 相应的计划网络图

（2）写出相应的规划问题

设xi是事件i的开始时间，1为最初事件，n为最终事件。希望总的配送时间最短，即目标函数就是求xn的最小值，设tij是作业 i,（ ）j的计划时间，则对于事件i与事件j有不等式 xj≥xi+tij，由此得到相应的数学规划问题：

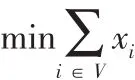
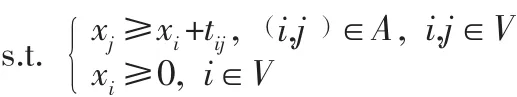
分别用xi，zi表示第i（ i=1,…,10 ）个事件的最早开始时间和最迟开始时间，esij，lsij，efij，lfij分别表示作业 （i,j ）的最早开工时间、最迟开工时间、最早完工时间、最晚完工时间。找出最早开工时间与最迟开工时间相同的作业，就能得到项目的关键路径。

根据问题，有下面的递推公式：

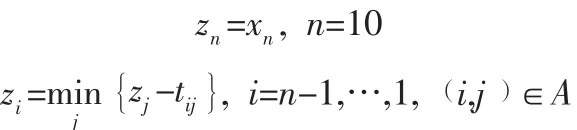
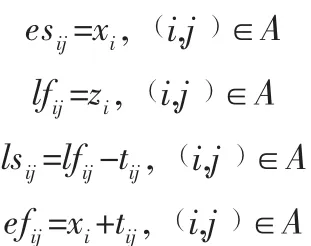
（3）运用Lingo软件对上述规划问题求解

Lingo程序如下：

model:

sets:

events/1..10/:x,z;!x为事件的最早时间，z为事件的最迟时间;

operate（ events,events ）/1 2,1 3,2 4,3 7,4 7,4 5,4 6,6 5,7 8,5 9,8 9,9 10/:t,s,ls,es,ef,lf;!s为松弛变量，ls为作业的最迟开工时间，es为最早开工时间，ef为最早完工时间，lf为最迟完工时间;

endsets

data:

t=1 3 2 2 2 3 3 2 3 2 1 2;

@text（ txt 1.txt）=es,ls;!把计算结果输出到外部纯文本文件;

enddata

min=@sum（ events:x）;

@for（ operate（ i,j ）:x（j）>x（i）+t（ i,j ））;

n=@size（ ev ents）;

z（n）=x（n）;

@for（ events（i）|i#lt#n:z（i）=@min（ operate（ i,j）:z（j）-t（ i,j ）））;

@for（ operate（ i,j ）:es（ i,j ）=x（i ））;

@for（ operate（ i,j ）:lf（ i,j ）=z（j ））;

@for（ operate（ i,j ）:ls（ i,j ）=lf（ i,j ）-t（ i,j ））;

@for（ operate（ i,j ）:ef（ i,j ）=x（i）+t（ i,j ））;

end

运行程序，得出的结果如表2所示，方括号中第1个数字是最早开工时间，第2个数字是最迟开工时间。

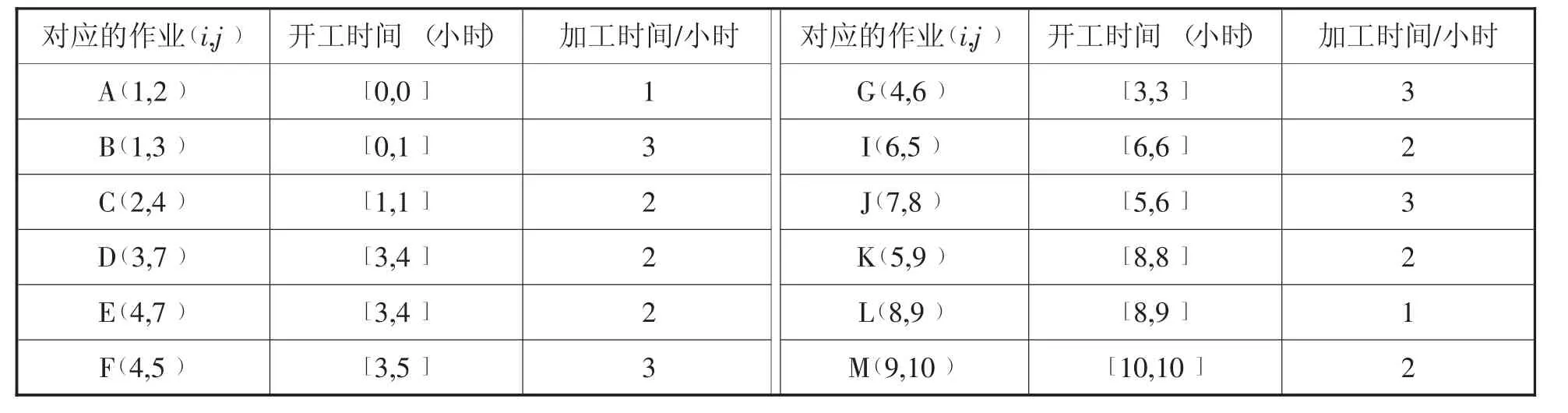
表2 作业数据

当最早开工时间与最迟开工时间相同时，对应的作业就在关键路线上，因此可以根据表2看出关键路线为A→C→G→I→K→M。

关键路线是整个计划网络的最长路线，现在关键路线长度为1+2+3+2+2+2=12，也就是说，在最坏的情况下，V1企业为V10企业进行物流派送所花费的最长时间为12个小时，等于V10企业所要求的12个小时。因此V1企业可以为V10企业进行及时的物流派送。

5 结束语

本文研究了关键路径法在冷链物流中的应用，对相关的问题建立了模型，并通过Lingo软件对该模型进行求解，得到关键路径的长度满足配送时效的要求，帮助该企业检测了物流配送的可行性。

[1] 胡运权，郭耀煌.运筹学[M].北京：清华大学出版社，2012.

[2] 翁心刚，安久意，胡会琴.冷链物流[M].北京：中国财富出版社，2016.

Application of Critical Path Method Based on Lingo in Cold Chain Logistics

CAO Qian,SONG Xiaoying (Shanghai University of Electric Power,Shanghai 201399,China)

Cold chain logistics is a new form of logistics which developed recently,and the logistics enterprises consider in many aspects for the cold chain distribution.This paper mainly studies the application of critical path method in cold chain logistics. By analyzing the example,we solve the timeliness for the cold chain logistics distribution with the Lingo software.

critical path method;cold chain logistics;Lingo

U116.1

A

1002-3100(2017)08-0043-03

2017-06-05

国家自然科学基金项目，项目编号：61303010。

曹 茜（1982-），女，辽宁沈阳人，上海电力学院经济与管理学院， 副教授，博士，研究方向：物流与生产调度。