基于混合遗传算法的框架式物流车配送路径优化

张新敏，张 卉，萧绮琪 ZHANG Xinmin,ZHANG Hui,XIAO Qiqi

（沈阳工业大学 机械工程学院，辽宁 沈阳 110870）

基于混合遗传算法的框架式物流车配送路径优化

张新敏，张 卉，萧绮琪 ZHANG Xinmin,ZHANG Hui,XIAO Qiqi

（沈阳工业大学 机械工程学院，辽宁 沈阳 110870）

框架式物流车是一种承载量高、配送物品多样化、配送过程稳定、装卸物品方便、节省能耗的物流配送车辆。对于节拍性较强、生产工位需求多样且需求量大的生产现场物料需求特点，框架式物流车无疑是最佳选择。文章针对一条定时配送的装配生产线以成本最小为目标进行配送路径优化。由于配送过程中还要进行废品料箱的回收且与物料配送不同时进行，所以优化后的配送路径不唯一。对于优化过程中遗传算法易陷入局部最优解及易早熟的缺点，文章设计了一种混合式遗传算法，将模拟退火法及遗传算法相结合，以加快收敛速度得到全局最优解，最后通过实际分析来验证方法的可行性。

框架式物流车；定时配送；混合遗传算法

0 引言

框架式物流车具有转弯半径小、承载量高、配送物料多样化、配送过程稳定、装卸物品方便、节能等优点，因此在节拍性强，生产工位需求多样且需求量大的汽车装配生产车间成为一种重要的物料运输设备。对其路径进行科学合理规划对保证生产物流需求、降低物流成本有重要意义。车辆路径问题（VRP）的研究自Dantzig[1]首次提出以来一直受到关注。Juny[2]等人改进了启发式算法，避免了优化过程中出现局部最优解。Subramanian[3]等人提出将边访问次数作为新模型，构造出Lazy约束来调整路径，进而增加解的可行性。Goksal[4]等人将PSO和VND方法进行混合，用这种混合方法来求解VRP问题。国内对于VRP问题的研究相比国外发展的较晚，钱艳婷[5]将时间点等时间窗的概念加入到动态车辆路径问题中，并结合节约法和禁忌搜索法来高效地解决动态路径规划的问题。邢永峰[6]将正向和逆向物流结合成一个整体来看待，用自适应算法求出最优解，大大提高了运算的效率。近年来也有许多学者研究了用改进遗传算法解决VRP问题[7-8]。与一般的VRP不同的是，框架式物流车在进行生产物流配送时是多辆车对多个工位的求解问题，在其途经的若干站点往往还要回收废品物料且数量和与物料的正常配送时间间隔不同，即需要考虑废料的产生与物料配送的关系，导致优化路径存在多样性。本文的数学模型就是综合以上多种因素结合以成本最小为目标构建的。遗传算法是其求解的一种典型算法，针对遗传算法的不足，本文设计了一种混合遗传算法实现对多个框架式物流车的路径规划。

1 问题描述和数学模型建立

本文中物流车辆配送行驶路径问题可以描述为：生产线有一个配送中心，共有m辆物流配送车，一共有n个工位需要进行物料配送，即n（ n=0,1,2,…,n ）个需求点，工位i的需求量为qi，0≤qi≤Qk，i=1,2,3,…,n，k=1,2,3,…,m，其中Qk表示车辆k的承载能力，以配送成本最低为目标建立的目标函数为：

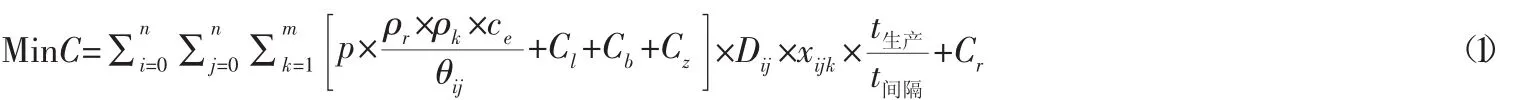
约束条件：

其中：P表示物流配送车的额定功率，ρr表示车辆行驶工况系数，ρk表示生产现场道路拥堵系数，Ce表示工业耗电单价，Cl表示单位里程轮胎磨损成本，Cb表示单位里程保修费用，Cz表示单位里程折旧费用，Cr表示人工每天成本，θij表示工位i到工位j的行驶速度，Dij表示工位i到工位j的行驶距离。

式（4）确保到达各工位的车辆最终会驶离，式（5）、式（6）确保每个工位只能被分配到一条路径中，式（7）约束了每辆车的载重不能大于额定载重量。

2 混合遗传算法

遗传算法能以较大的概率搜索出最优解，但是容易早熟。模拟退火法可避免陷入局部最优解，能够保证全局最优解的可靠性。针对两种算法的特点，将两种算法结合，形成一种混合遗传算法，结合后将遗传算法的种群进化变成单个个体进行进化，进化过程由交叉和变异变成模拟退火的过程。具体步骤如下：

（1）对染色体编码。编码方法常用的有实数编码和二进制编码。由于使用二进制编码在算法运行时效率低，而且对混合算法的实现产生负面影响，所以本文采用实数编码的方式，也就是将真实值作为编码，把编码按顺序连接在一起，形成个体编码串。需要解码时只要将每个染色体基因座上的基因值按顺序赋值给变量即可。

（2）适应度函数。适应度代表着最优解的优良程度，在运算的交叉、变异等算子以及约束条件和目标函数的共同作用下才能构造出个体适应度函数。在本文设计的混合遗传算法中可以将退火罚因子加入到适应度函数中：

其中：minC为目标函数，αi为退火罚因子，随着混合遗传操作的进行，温度随之降低，目标函数越小，适应度函数的值越大，适应性越强，个体越优秀，反之个体越差，而适应度函数值越大的有更大的机会去繁殖后代个体，使优秀的基因能够遗传下去。

（3）选择操作。采用正规几何排序选择法。对目标极大极小问题都适用，适应度并不一定要求非负，不需要具体数据，只涉及个体适应度大小顺序。基本思路是按照适应度大小对种群中的所有个体进行排序，群体中各个个体被选中的概率为:

其中：q为最优个体的可能性，在 0,0.（ ）1范围内变化，由编程后台取得；r是个体的排序编号；M是种群规模。

（4）交叉操作。用非均匀算数交叉。将完成选择后的个体进行交叉运算，非均匀算数交叉的具体方法如下：

假设现有两个个体At和Bt，现进行交叉，经过非均匀算数交叉后的个体为：

其中：a=exp（-a0·T/t）；a0为非均匀交叉系数，a0的取值范围虽然为 [0,1 ]，但是a0得取值越靠近1则交叉越均匀，所以a0的选择不宜过大；T为进化的最大代数；t为当前进化代数。

（5）变异操作。采用均匀变异，其过程为：

其中：U为变异过程中的变异算子，数值范围为 [0,1 ]，Umax为变异能达到的最大值；Umax（xk）为当前个体xk最大的变异值；c1,c2是均匀分布在 [0,1 ]上的随机数，c1=1-c2，具体数值精确到小数点后一位。

（6）模拟退火操作。经过遗传算法的交叉变异操作后将新得到的个体带入到模拟退火算子的计算中，以得到新的个体。

（7）动态的交叉和变异。当遗传算法进化到不同时期时，如果交叉率和变异率始终取相同值会影响算法的进化，尤其到了后期，个体的相似度较高，变异率应该变大，交叉率而应减小，以此来减轻交叉作用增强变异作用。

其中：Fmin是存活下来的个体的最小适应度数值；F为存活下来所有个体的适应度数值的平均数；F'是比较交叉后两个个体的适应度数值中较小的值；y和u是不同的调整系数，取值在 0,（ ）1之间。

（8）求得最优解。

3 应用实例

框架式物流车因其转弯半径小且子车可以根据生产现场需求状况串联使用而具有诸多优点。且可以很好地弥补定时配送的缺点，提高配送效率。其外观如图1所示。

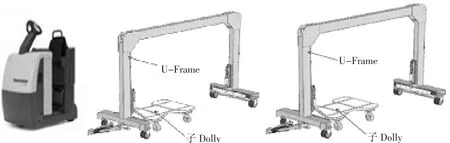
图1 框架式物流车

在某发动机装配车间现场有10个工位均有配送需求，计量单位均为kg，满载的额定重量为100kg，各工位之间的配送距离用Dij表示，配送中心用0表示且位置固定，物流配送车从配送中心出发，车辆所装的货物总重量不能超过车辆的承载，每个工位最多可被一辆物流配送车服务，在满足配送需求下，求出最小成本的路线。在本论文中的成本包括电力消耗、保修成本、折旧成本及人工成本。生产线的简图及最初行驶路线如图2所示，增加的废料箱更换及回收布局图如图3所示。

图2 工位示意图

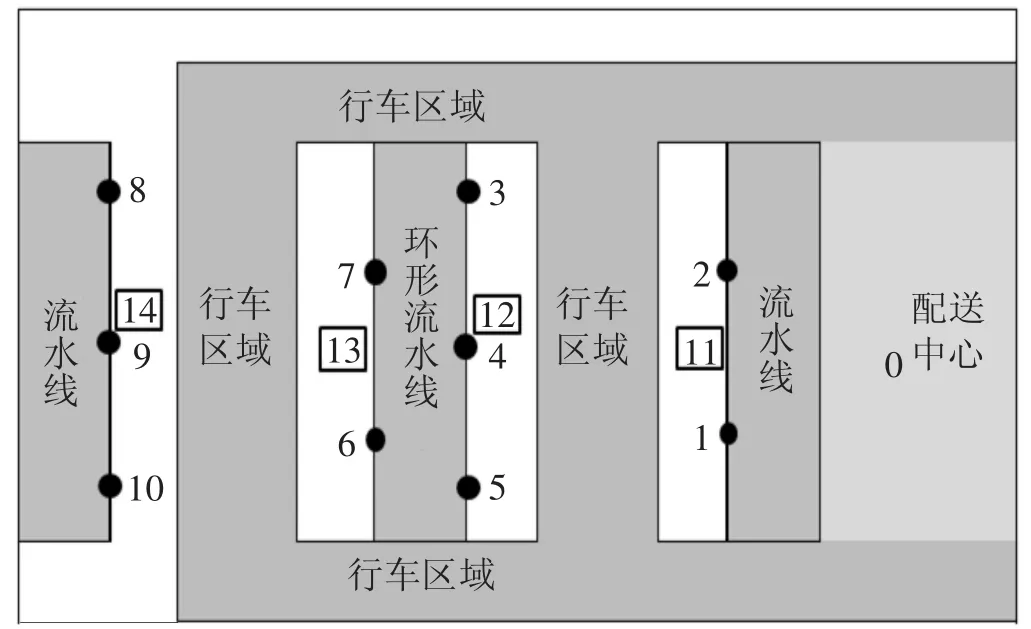
图3 加入物料箱后布局图

现有行驶路线如表1所示。

表1 现有行驶路线

图2所显示的是route1的行驶配送路线；图3的11、12、13、14工位为物料箱放置点，现有的行驶路线中每90分钟单独用一辆物流车对四个废品料箱进行统一更换。

各工位及各工位之间的相关情况如表2至表6所示：

表2 各工位所需零件重量

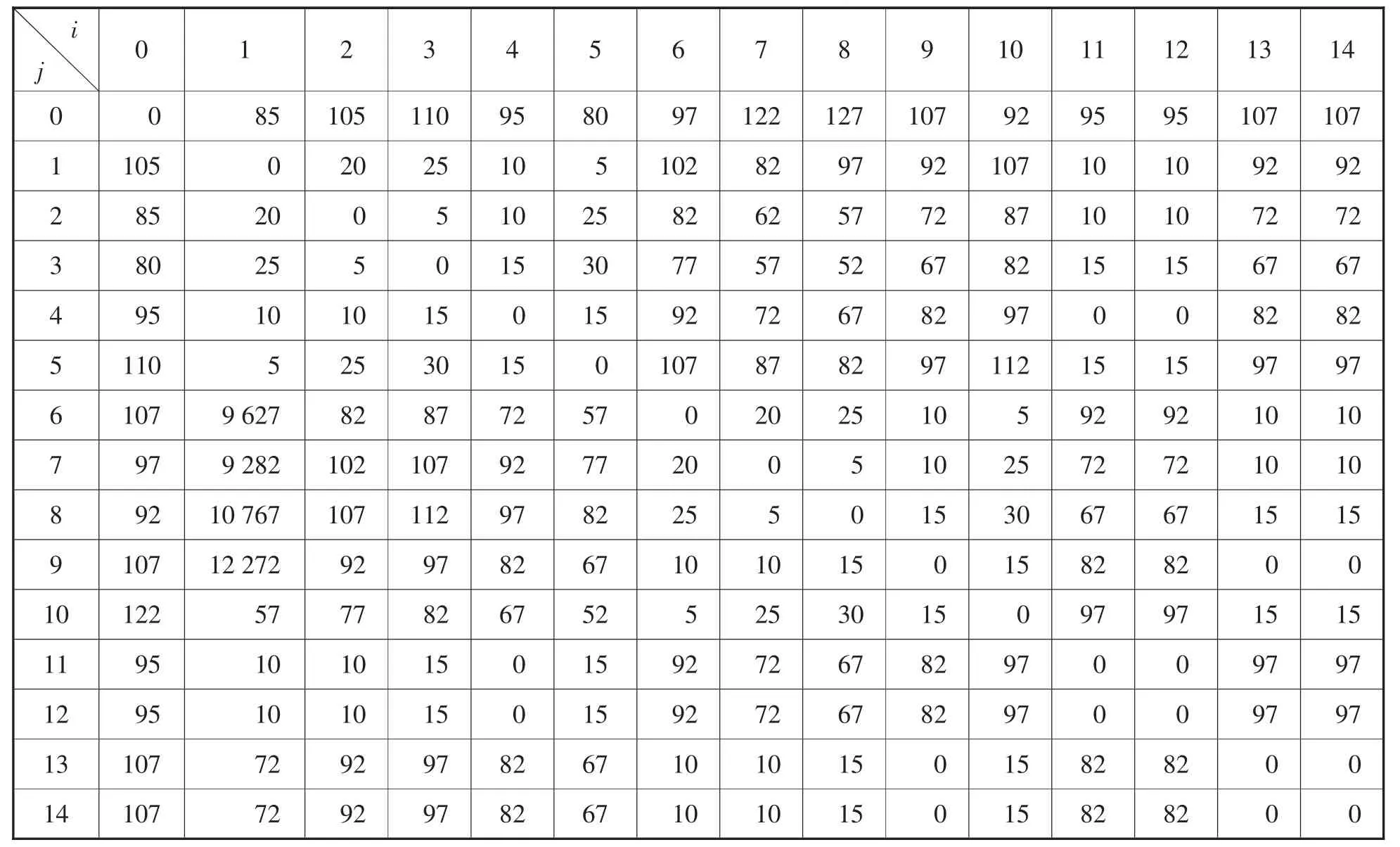
表3 各工位之间的距离 Dij（ ）

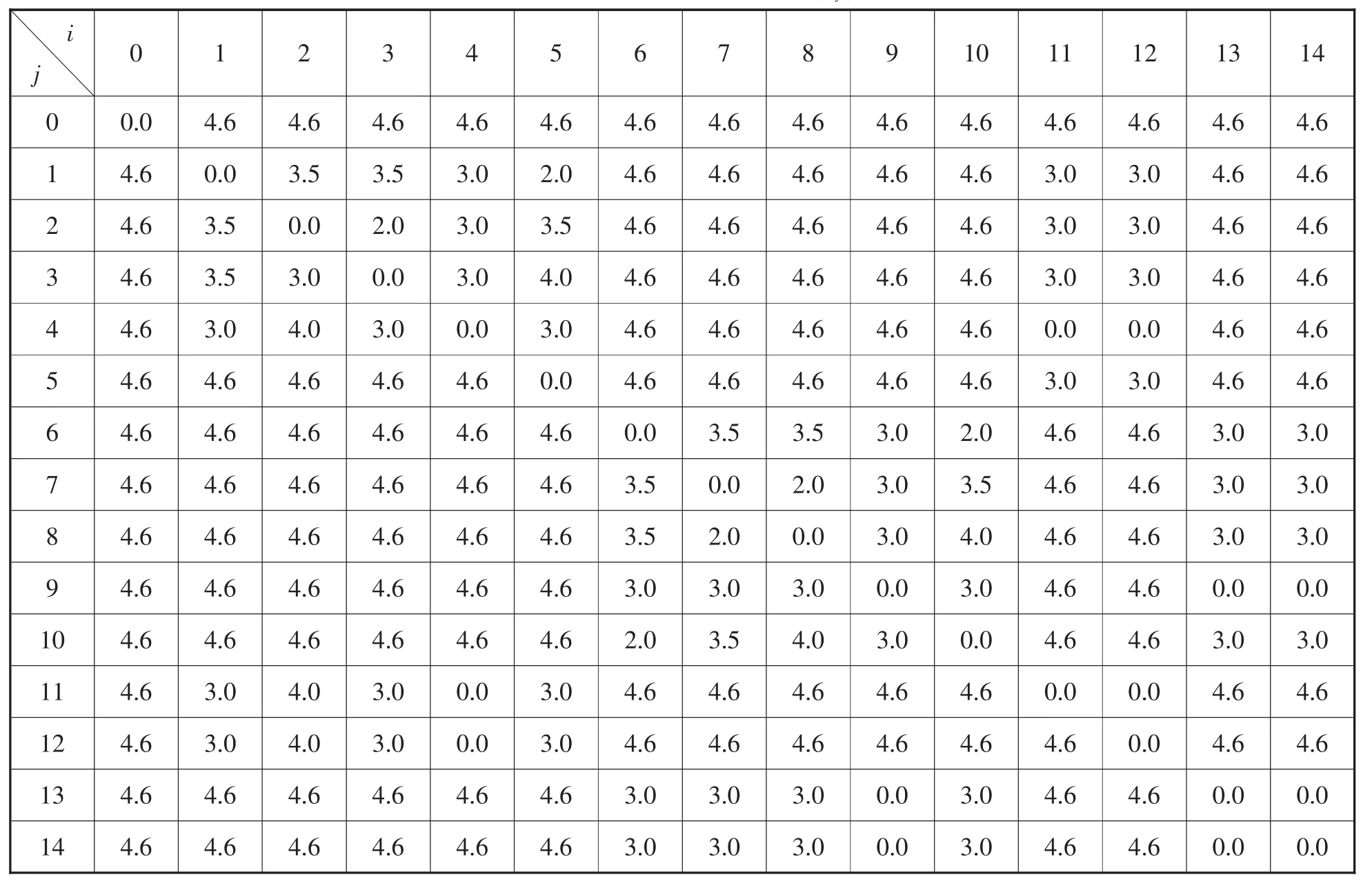
表4 工位之间的行驶速度 θij（）

表5 各工位之间的行驶工况系数 ρr（）

表6 各工位之间的拥堵系数 ρk（）

本文中的Cr、Ce、Cl、Cb、Cz是根据生产现场的实际情况给出的，Cr是将工人的月工资折合成天进行计算180元/（天*人），Ce是工业耗电费用0.8896元/kwh，Cl为2元/km，Cb为8元/km，Cz为0.1元/km，P为2.8kw/h。

原路径由于成本因素单一、数据对称导致的成本差异如表7所示。

利用编程求出最优解，其中设置迭代次数为300次；交叉概率为0.8；变异概率为0.1；种群规模为30；降温次数为100；每个温度迭代步长为3；初始温度为250.00；降温系数为0.98。经过编程运算得到结果如表8所示。

根据实际生产情况，生产配送的时间间隔为30min，需更换废料箱的时间间隔为90min，所以在表8中有两种配送方案，

表7 成本差异表

表8 优化结果对比

第一种为每30min配送，第二种为每90min配送。而对比两种方法的收敛曲线不难发现，混合遗传算法要比普通的遗传算法收敛速度快，最优解要优于遗传算法，如图4所示：

图4 算法收敛对比图

4 结 论

以配送成本最小为目标建立了生产线配送数学模型，将产生配送成本的因素加以整合，多种影响因素均转化为车辆行驶的相应系数并体现在成本中。通过所设计的混合遗传算法求解该模型求出了成本最小的行驶路线。通过对普通遗传算法和本文算法的对比表明，本文算法在速度，搜索范围，局部搜索能力等方面均优于普通遗传算法。针对废品料箱的更换与物料配送二者时间间隔不同的问题，运用两种配送方案进行定时配送从而节省配送成本。针对生产线的工位需求超出物流车额定载荷的突发问题，提出了虚附加工序的方法并将其融入目标函数中，求解结果在成本和路径方面均优于现有突发问题路径方案，且提高了框架式物流车的利用率。

[1] Dantzig G B,Ramser J H.The truck dispatching problem[J].Managemant Science,1959(6):80-91.

[2] JUNY,KIMB.New best solutions to VRPSPD bench mark problems by a perturbationbased algorithm[J].Expert Systems with Applications,2012,39(5):5641-5648.

[3]SUBRAMANIAN A,DRUMMOND L M A,BENTES C,et al.A parallel heuristic for the vehicle routing problem with simultaneous pickup and delivery[J].Computers and Operations Research,2010,37(40):1899-1911.

[4] GOKSAL.FP,KARAOGLAN I,ALTIPARMAK F.A hybrid discrete particles warm optimization for vehicle routing problem with simultaneous pickup and delivery[J].Computers&Industrial Engineering,2013,65(1):39-53.

[5] 钱艳婷.多动态目标车辆路径问题的算法研究[D].天津：天津大学（硕士学位论文），2011.

[6] 邢永峰.电子商务物流系统中回程带货的车辆路径问题研究[J].物流技术，2014(8):226-229.

[7] 王超，穆东.物料配送和废旧产品回收的VRPSDP问题的并行模拟退火算法[J].北京交通大学学报，2014,38(6):19-26.

[8] 张瑞峰，汪同三.新型遗传算法求解车辆路径问题研究[J].湖北大学学报，2012,34(2):240-242.

Distribution Routing Optimization for U-frame Vehicle Based on Hybrid Genetic Algorithm

(School of Mechanical Engineering,Shenyang University of Technology,Shenyang 110870,China)

U-frame is a logistics vehicle which has high carrying capacity,diversification of distribution items,stable distribution process,energy-saving and it is easy to load and unload items.For the situation of workshop material distribution with distinct tact time,diverse requirements from different workstation and large demand of quantity,the U-frame is a suitable choice.The material distribution and discarded products recovery are not performed at the same time.The route is optimized with the object that the comprehensive cost is minimum.To solve the model,a combination of simulated annealing and genetic algorithm is presented to overcome defects in precocity and low convergence speed for conventional genetic algorithm.Therefore,high convergence speed and global optimal solution are obtained.At last,a route optimization is performed on material distribution to an auto assembly line to illustrate the effectiveness of the proposed method.

U-frame;regular distribution;hybrid genetic algorithm

F252.14

A

1002-3100(2017)08-0027-06

2017-05-15

张新敏（1964-），男，吉林长春人，沈阳工业大学机械工程学院工业工程系主任，教授，工学博士，中国机械工程学会工业工程分会理事，研究方向：精益生产、计算机辅助监控、管理信息系统、质量管理与控制、设施规划与物流分析；张 卉（1991-），女，辽宁沈阳人，沈阳工业大学机械工程学院硕士研究生，研究方向：设施规划与物流分析。