基于悬架KC特性的车辆动力学参数化建模方法*

闫瑞雷

（广州汽车集团股份有限公司汽车工程研究院）

车辆动力学仿真是汽车仿真技术的重要组成部分[1]，在车辆研发初期，通过虚拟仿真替代场地试验对整车性能的优化匹配以及新产品开发能力的提升至关重要。目前，国内外各大车企普遍使用基于各杆系间拓扑结构建立的动力学模型进行虚拟仿真，如ADAMS[2]。该建模方法能够准确反映实车中各杆系间的拓扑关系以及力的传递，但该建模方式也存在一些缺点，因此，无法研究单一KC特性对整车性能的影响。文章通过对汽车各子模块进行力学和运动学分析，建立基于悬架KC特性的车辆动力学参数化仿真模型并以稳态回转工况为例进行仿真计算，与客观试验数据及ADAMS进行对比，验证模型的精度与仿真效率，为悬架系统的改进、底盘系统的开发及调校提供指导方向。

1 车辆动力学模型的建立

1.1 假设条件及坐标系建立

将汽车简化为一个多刚体系统，包括车身和4个车轮共5个质量刚体，在此基础上建立以转向盘转角和轮心合力矩为输入的车辆14自由度动力学模型，包括关于车身坐标系的3个平移自由度（x，y，z）、3个转动自由度（φ，θ，ψ）、4个车轮的垂直跳动自由度及4个车轮的自旋自由度。

为了便于汽车各个系统的受力分析和运动姿态的确定，分别建立描述车辆空间运动状态的惯性坐标系OXYZ（定义为坐标系N）、确定车身姿态的车身坐标系oxyz（定义为坐标系A）、定义轮胎受力的轮胎坐标系OwXwYwZw及在车身坐标系与轮胎坐标系之间起过渡作用的中间坐标系ObXbYbZb（定义为坐标系B），并且规定以上4组坐标系的横坐标、纵坐标及垂坐标均以向前、向左、向上为正，如图1所示。

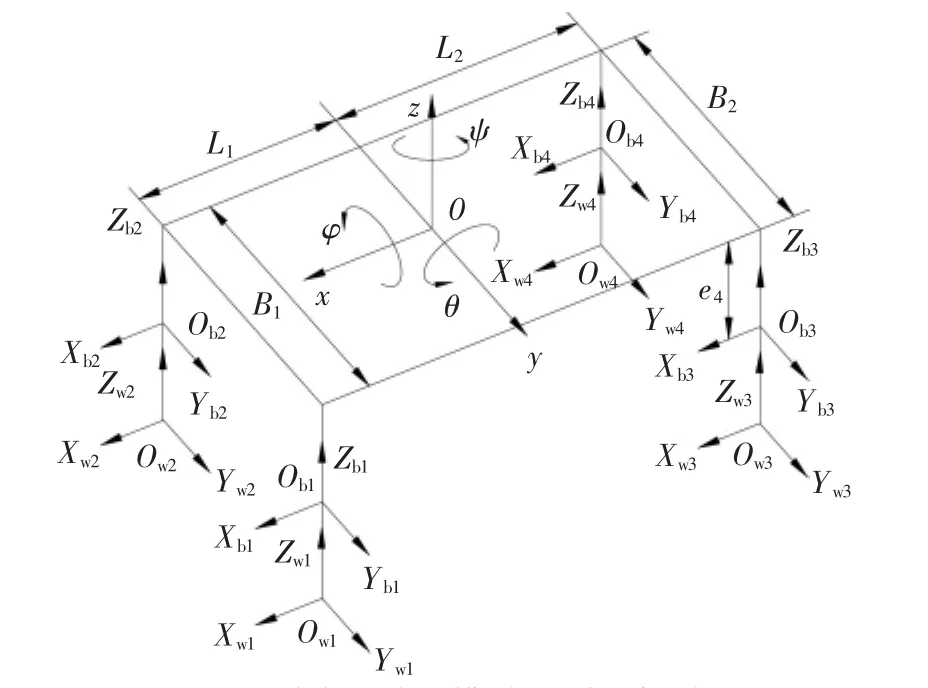
图1 车辆动力学模型及坐标系定义

坐标系B与坐标系A之间可通过坐标转化进行变换[3]，即：

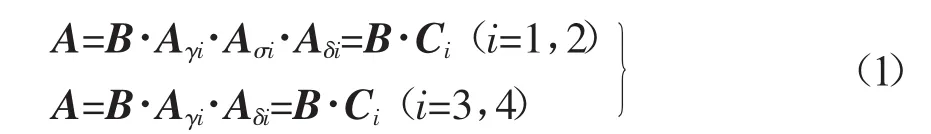
式中：Ci——坐标系A与坐标系B之间的方向余弦矩阵；

Aγi，Aσi，Aδi——坐标系B分别绕Xbi，Ybi，Zbi旋转γi，σi，δi角的方向余弦矩阵；

γi，σi，δi——车轮外倾角、自旋角及车轮转角，（°）。

定义车轮姿态的外倾角、自旋角及车轮转角具体表示如下：

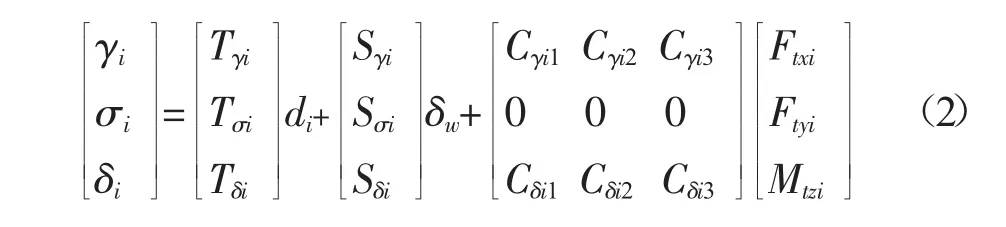
式中：δw——转向盘转角，（°）；

di——轮跳量，mm；

Tγi，Tσi，Tδi——轮跳外倾梯度、轮跳自旋梯度及轮跳前束梯度，（°）/mm；

Sγi，Sσi，Sδi——车轮外倾角、自旋角及车轮转角随转向盘转角变化的梯度，（°）/（°）；

Cγi1，Cγi2——车轮外倾角随纵向力及侧向力变化梯度，（°）/N；

Cγi3——车轮的外倾角随回正力矩变化的梯度，（°）/N·mm；

Cδi1，Cδi2——车轮转角随纵向力、侧向力变化梯度，（°）/N；

Cδi3——车轮的转角随回正力矩变化的梯度，（°）/N·mm；

Ftxi，Ftyi——轮胎接地点位置的纵向力、侧向力，N；

Mtzi——轮胎接地点回正力矩，N·mm。

参考式（1），可得坐标系A与坐标系N之间的方向余弦矩阵，定义为矩阵K。

为了便于描述车轮姿态，分别引入车身坐标系中的车轮单位法矢量（ωna1（i），ωna2（i），ωna3（i））和惯性坐标系中的车轮单位径矢量（ωrn1（i），ωrn2（i），ωrn3（i）），因中间坐标系的Yb轴与车轮单位法矢量共线，所以有：

将（ωna1（i），ωna2（i），ωna3（i））在坐标系 N 中表示为：

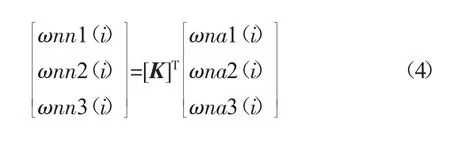
将（ωrn1（i），ωrn2（i），ωrn3（i））在标系 A 中表示为：

1.2 轮胎模型

轮胎力学特性对整车操纵稳定性分析至关重要，垂直载荷、车轮侧偏角、外倾角及纵向滑移率共同决定了轮胎的力学特性。

1.2.1 %轮胎垂直载荷计算

轮胎垂直载荷由其径向刚度和变形量决定，可表示为：

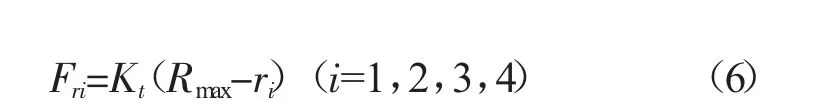
式中：Fri——轮胎垂直载荷，N；

Kt——轮胎径向刚度，N/mm；

Rmax——轮胎自由半径，mm；ri——径向滚动半径，mm。

1.2.2 %车轮侧偏角计算

侧偏角是指车轮中心线与速度方向的夹角，将车轮在惯性坐标系中的纵向速度（uni）和侧向速度（vni）沿车轮中心线分解（如图2所示），可得轮胎沿其中心线速度（uti）和垂直于中心线速度（vti）的关系式，如式（7）所示。

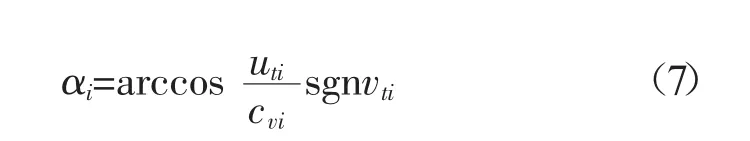
式中：αi——轮胎侧偏角，（°）；

uti——轮胎沿其中心线的速度，m/s；

vti——轮胎垂直于其中心线的速度，m/s；

cvi——车轮的合速度，m/s。

图2 轮胎接地点速度分解图

1.2.3 %车轮外倾角计算

外倾角是指车轮纵向平面与地面垂线所成的夹角，根据1.1节对单位矢量的定义，可将其表示为：

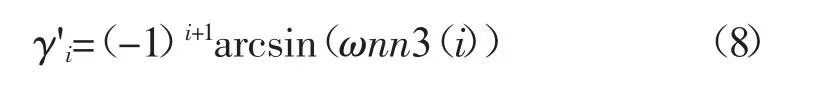
式中：γ'i——车轮外倾角，（°）。

1.2.4 %纵向滑移率计算

纵向滑移率对轮胎纵向力产生至关重要的影响，它是指车轮运动过程中，滑动成分所占的比例，即：

式中：κ——纵向滑移率，%；

Ωi——车轮转速，rad/s。

文章采用MF模型对轮胎6个分力进行计算，详细计算过程参照文献[4]。

1.3 悬架模型

悬架系统是汽车的车架与车桥或车轮之间的一切传力连接装置的总称，本节假设除确定轮胎姿态角及其受力分析之外，车轮只有相对于车身垂直跳动以及自身旋转2个自由度，其余4个自由度均不予考虑，简化悬架模型，如图3所示。

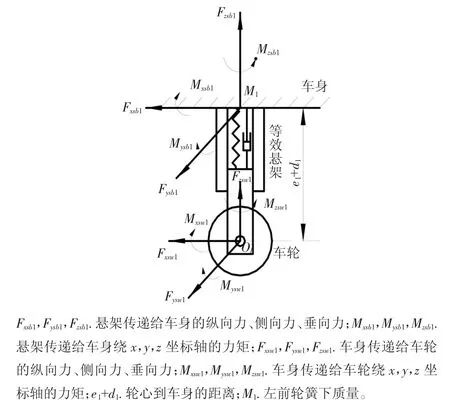
图3 汽车悬架简化模型图

1.3.1 悬架垂直力分析

悬架的垂直力主要有悬架预压力、弹簧力（F1）、阻尼力（F2）、抗纵倾力（F3）以及抗侧倾力（F4）。

1.3.1.1 悬架预压力

悬架预压力表示汽车处于静平衡状态下，簧上质量作用于轮心处的等效垂直载荷，可表示为：

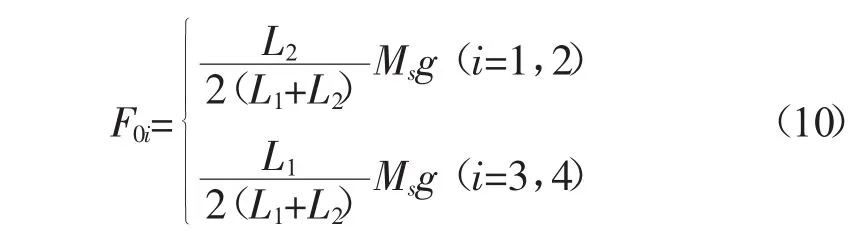
式中：F0i——悬架预压力，N；

L1，L2——质心到前后轴的距离，mm；

Ms——车身质量，kg；

g——重力加速度，取9.8 m/s2。

1.3.1.2 弹簧力

弹簧力由悬架动挠度和刚度决定，可表示为：

式中：F1i——弹簧力，N；

Csi——悬架刚度，N/mm。

1.3.1.3 阻尼力

减振器的阻尼力是由减振器阻尼和动挠度速度共同决定的，可表示为：

式中：F2i——减振器阻尼力，N；

Cdi——减振器阻尼，N·s/mm；

Di——轮跳速度，mm/s。

1.3.1.4 抗纵倾力

抗纵倾力是由纵倾中心在向车体传递力矩时产生的等效在悬架与车体连接点的垂向力[5]2-5，其表达式可表示为：

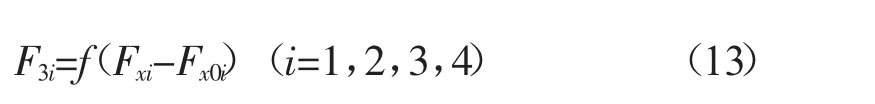
式中：F3i——抗纵倾力，N；

Fxi——车轮纵向力，N；

Fx0i——汽车静平衡时车轮纵向力，N。

1.3.1.5 抗侧倾力

抗侧倾力是由侧倾中心在向车体传递力矩时产生的等效在悬架与车身连接点的垂向力[5]2-5。抗侧倾力与轮胎侧向力的合力指向侧倾中心[6]，而侧倾中心的位置可通过车轮的侧向位移和垂向位移表示[7]，所以，抗侧倾力可表示为：

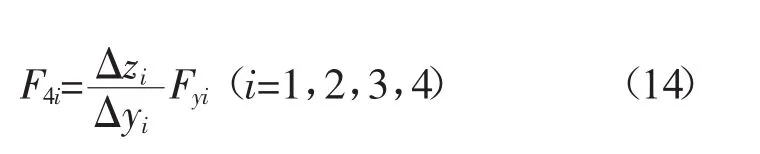
式中：F4i——抗侧倾力，N；

Δyi，Δzi——车轮侧向和垂向位移，mm；

Fyi——轮胎侧向力，N。

因此，总的悬架垂直力可表示为：

1.3.2 悬架垂直运动学分析

假设车轮在坐标系A中的速度矢量（UA）和坐标系A相对于坐标系N的角速度矢量（ΩA）分别为：

式中：ui，vi，wi——轮心在纵向、侧向及垂向速度，m/s；

p，q，r——车轮绕纵向、侧向及垂向转动的角速度，rad/s。

则坐标系A中车轮的加速度可表示为[8]60-62：

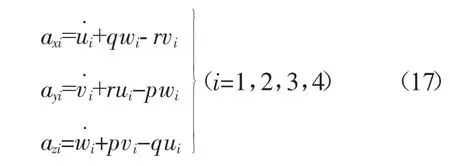
式中：axi，ayi，azi——车轮在x，y，z向的加速度，m/s2。

根据达朗贝尔原理[9]，列出坐标系A中各车轮垂向动力学方程为：

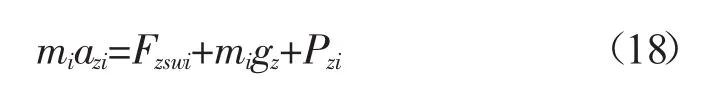
式中：mi——车轮质量，kg；

Fzswi——悬架系统作用于轮心处的垂直力，N；

gz——车轮在坐标系A中z方向的重力加速度，取9.8 m/s2；

Pzi——地面作用于轮心处的反作用力，N。

1.3.3 %车轮自旋运动分析

以驱动轮为例，在坐标系A中对车轮进行力学及运动学分析，如图4所示。

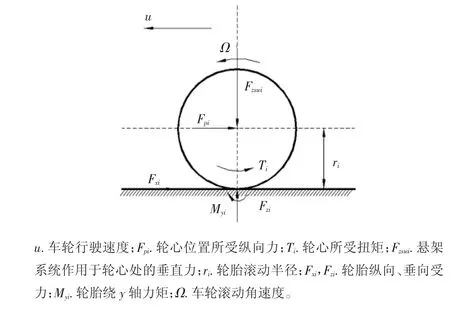
图4 车轮自旋模型图

根据达朗贝尔原理，建立力矩平衡方程式，如式（19）所示。

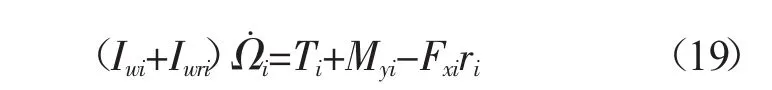
式中：Iwi——第i轮自旋转动惯量，kg·mm2；

Iwri——第i根半轴的自旋转动惯量，kg·mm2。

1.4 车身模型

汽车运动过程中，车身、车轮及悬架系统之间是相互耦合的，为了简化建模过程，对车身和4个车轮的垂向动力学方程进行单独建立，而纵向、侧向、横摆、侧倾及俯仰的动力学方程则以整车作为研究对象。

1.4.1 车辆运动学分析

根据式（17）可得坐标A下车身质心的加速度为：

式中：ax，ay，az——车身质心沿x，y，z向加速度，m/s2；

u，v，w——车身在纵向、侧向及垂向速度，m/s。

此外，根据牛顿-欧拉运动学方程[8]68可得作用在车身上的外力对车身质心的主矩为：

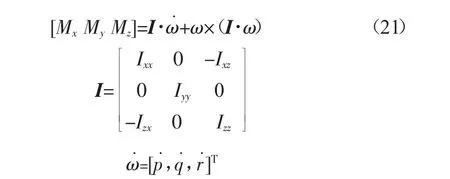
式中：Mx，My，Mz——车身上的外力对车身质心在x，y，z向的主矩，N·m；

ω——车身侧倾、俯仰及横摆的角速度，rad/s；

Ixz，Ixx，Iyy，Izx,Izz——车身转动惯量，kg·mm2。

1.4.2 车辆受力分析

将整车视为研究对象，在坐标系A中对其进行受力分析，建立力（力矩）平衡方程式，如式（22）所示。

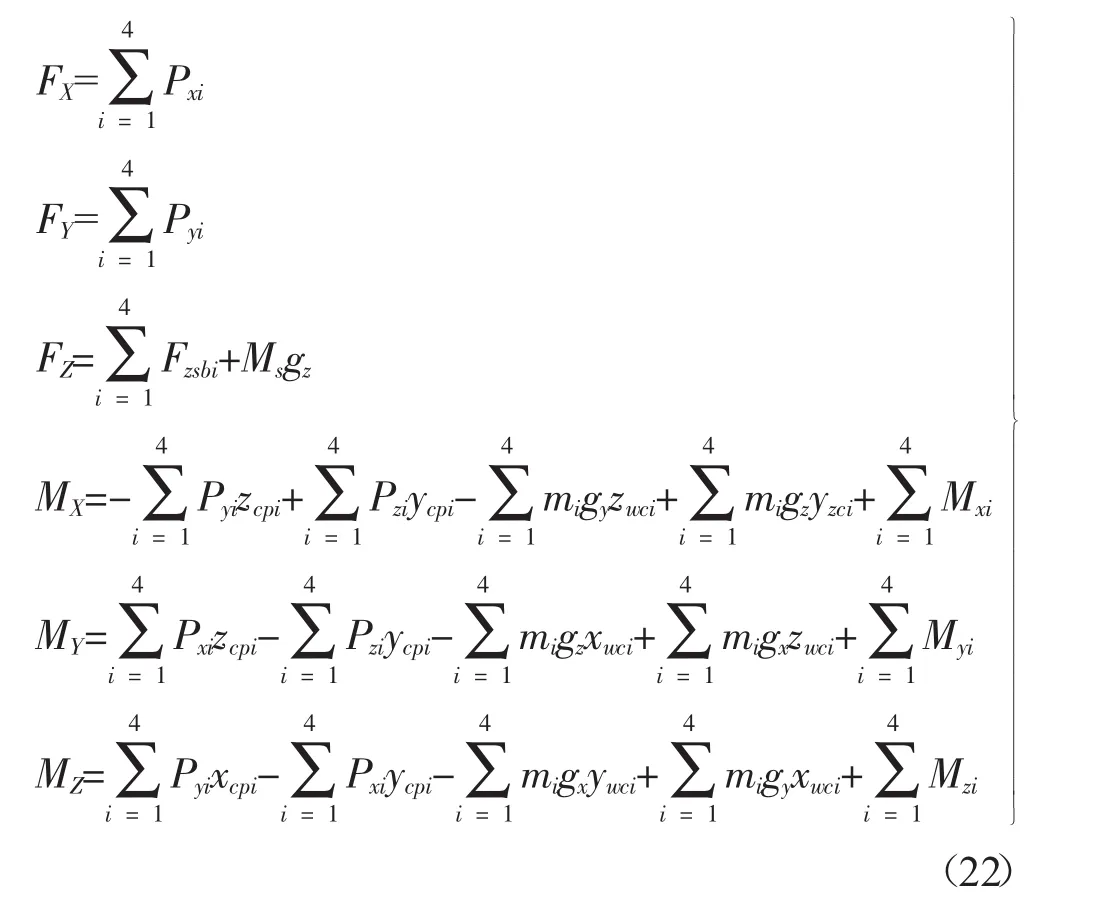
式中：xwci，ywci，zwci——车身坐标系下轮心坐标，mm；

xcpi，ycpi，zcpi——车身坐标系下轮胎接地点坐标，mm；

gx，gy，gz——重力加速度在坐标系A下x，y，z向的分量，m/s2；

FX，FY，FZ——车辆在X，Y，Z向的合力，N；

Pxi，Pyi，Pzi——轮胎接地点x，y，z向的受力，N；

Mxi，Myi，Mzi——轮胎接地点绕x，y，z向的力矩，N·mm。

根据以上对车辆的运动学分析和受力分析，可列出车辆在车身坐标系中动力学方程，如式（23）所示。

因此，式（18）、（19）及（23）组成整车动力学微分方程组。

1.5 动力学模型求解计算

上述动力学微分方程组是由14个微分方程组成的，方程与方程之间存在复杂耦合关系，利用常见的数值方法进行求解并不能满足实时仿真的要求。本节在迭代思想的基础上，采用欧拉法[10]对微分方程组进行求解，即：

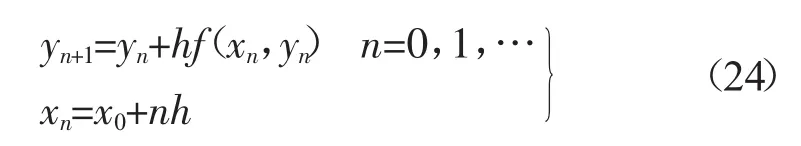
式中：x0——自变量初始值；

h——步长；

xn，yn——第n个自变量和因变量。

首先将微分方程组化解，把每个方程中的状态变量分为含二阶导数项的状态变量、含一阶导数项的状态变量及不含导数项的状态变量，其中将含二阶导数项的状态变量放置方程的左边，其余状态变量以及力向量放置方程的右边，此时，微分方程组可表示为：

N——除二阶导数项之外的状态变量和力向量组成的10×1向量；

D1，D2，D3，D4——4个车轮跳动速度，mm/s。

通过求解M-1，得到含二阶导数项的状态变量，即：=M-1·N，根据初始条件（X0）和 h 对方程组进行求解，并按照欧拉公式进行迭代计算，从而得到坐标系A下描述车辆运动的各状态变量，如位移、速度、侧倾角及横摆角速度。

2 仿真验证

本节以稳态回转工况为例，结合相应的ADAMS整车模型以及客观试验数据，利用所建的14自由度车辆动力学数学模型对整车进行仿真计算，从仿真结果与运行效率两方面进行对比分析，验证数学模型的准确性与高效性。样车的主要参数，如表1所示。

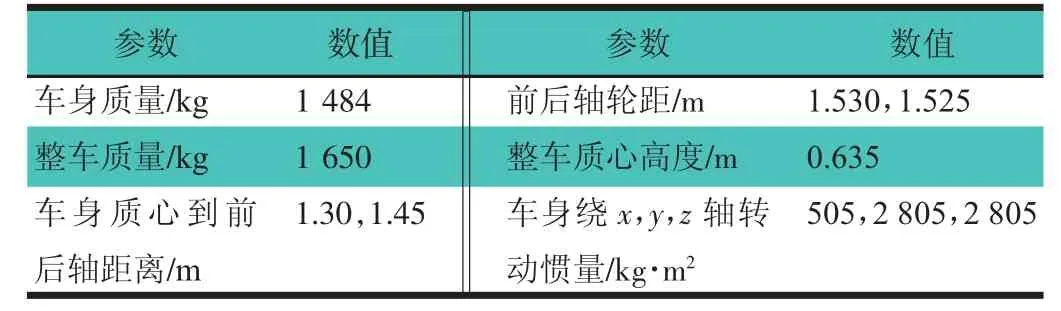
表1 样车主要参数

2.1 稳态回转

稳态回转试验包括定半径和定转向盘转角2种试验方法，主要用于评价汽车达到稳定行驶状态时的稳态横摆响应，本节利用数学模型对车辆进行30 m定半径稳态回转试验工况进行仿真计算，通过对比分析行驶过程中车辆侧向加速度与转向盘转角、横摆角速度及车身侧倾角的仿真曲线，验证数学模型的准确性，如图5所示。

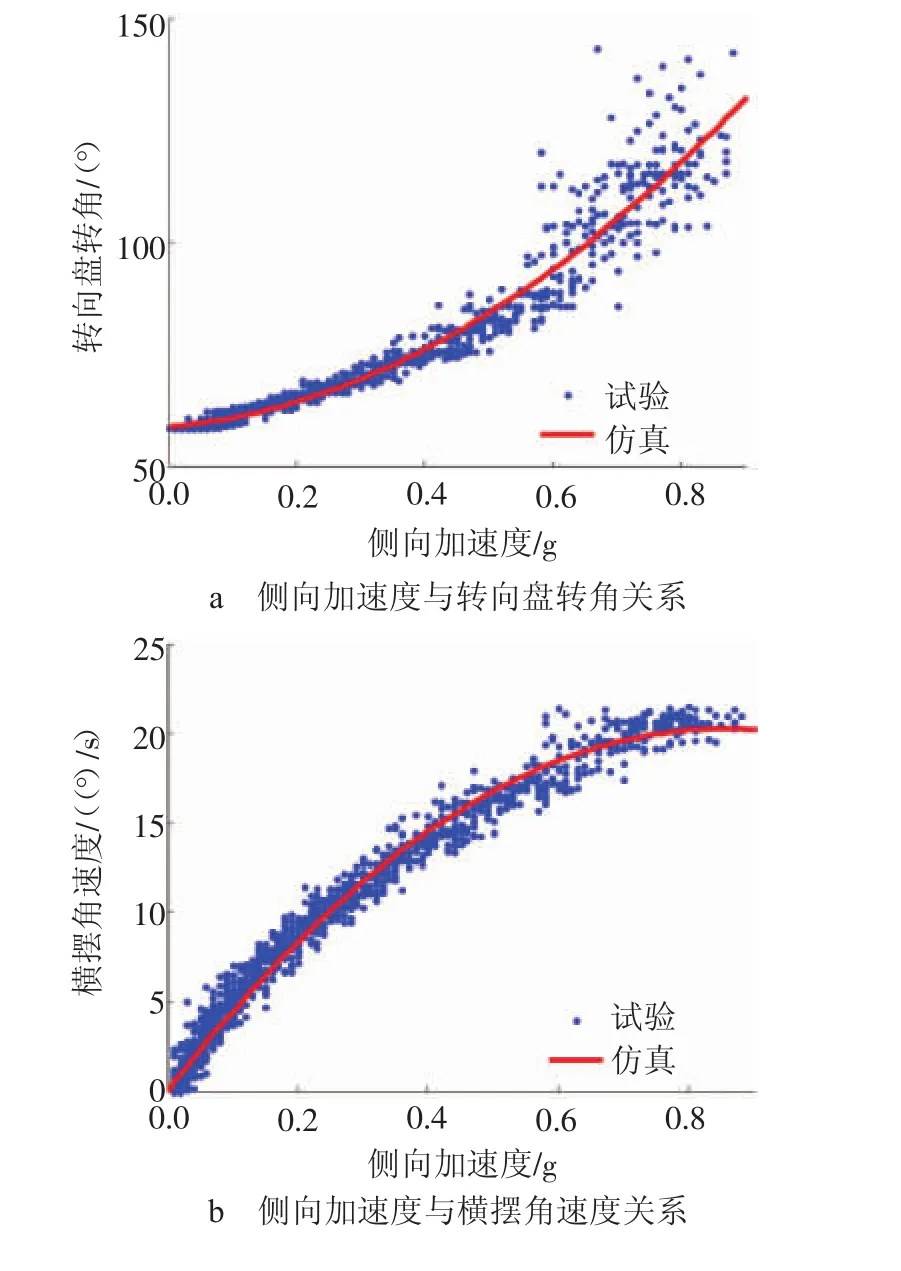
图5 汽车30 m定半径稳态回转试验工况对比

通过对比分析稳态回转试验工况下，横摆角速度、车身侧倾角及转向盘转角随侧向加速度的变化曲线可知，试验数据与计算结果的吻合情况良好，从而证明，数学模型能够准确描述车辆稳态回转工况下的运动状态。

2.2 仿真速度对比

分别利用数学模型和相应的ADAMS模型，以相同的仿真时间及仿真步长对直线制动、转向盘角阶跃输入、稳态回转工况进行仿真，并记录各自CPU运行时间，如表2所示。

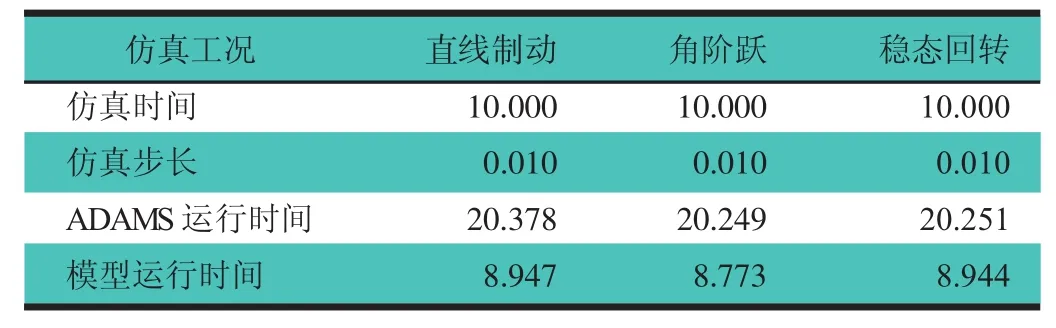
表2 动力学模型的仿真速度对比 s

由表2可知，在仿真时间与仿真步长相同的情况下，二者仿真工况设定时间与CUP完成计算所需运行时间之间的比值大概分别是1∶0.89和1∶2.03，数学模型的运算速度比ADAMS模型提高了56.2%左右。

3 结论

1）基于悬架KC特性建立的参数化车辆动力学模型不受悬架结构的限制，具有较强的通用性，且可以在保证较高的仿真精度的同时，有效提高计算速度；

2）模型的建立依托于悬架KC特性曲线，与悬架硬点无关，可以研究单一KC特性对整车性能的影响，便于整车性能目标分解；

3）在迭代思想的基础上，采用欧拉法对微分方程组进行求解，将求解结果与客观试验数据及ADAMS进行对比分析，从而验证数学模型的仿真精度与运算速度，为车辆动力学开发提供了指导价值。