电动汽车用锂离子电池的建模与SOC估算

童佳俊 方忠慧 端鹏 齐国庆 张莉娟

（南京中欧威能新能源动力系统有限公司）

电池的荷电状态（SOC）反映的是电池的剩余电量。SOC的估算是电池管理系统（BMS）中的一项关键技术，也是整个系统设计的难点之一，其估算的准确度将直接影响到整车的控制策略。目前通常采用的方法是建立电池的等效电路模型来分析电池外部特性从而计算SOC，而传统的Rint和Thevenin电池模型其结构较为简单，精度不高，并且目前国内外产品中普遍采用的SOC计算方法是安时积分法，这种估算方法虽然原理较为简单，易于实现，但是其估算精度有限，依赖于SOC初值，并且容易产生累计误差。基于以上问题，该文采用了2阶RC等效电路模型，并运用扩展卡尔曼滤波算法（EKF）来估算SOC，经过仿真验证，达到了预期的效果。

1 等效电路模型

1.1 2阶RC等效电路模型

电池的充放电过程是一段复杂的电化学过程，为了确定其电压、电流、SOC及内阻等特征量之间的数学关系，首先需要建立电池的等效模型，如图1所示。Thevenin模型具有较为良好的非线性，能够模拟出电池的充放电特性，并且模型较为简单，便于计算，因此得到了广泛应用，其电路结构，如图1a所示，模型中使用单RC环来表示电池的极化现象。然而在电池实际的充放电过程中存在着多个极化现象，例如：浓差极化和电化学极化等，因此可以在模型中采用多个RC环相串联来表示不同的极化现象，从而提高电池模型的精度，但同时这样计算量也会大大增加，通过权衡模型精度以及计算难度后，文章采用2阶RC的等效电路模型，如图1b所示。

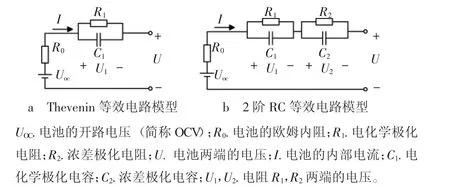
图1 电池等效电路模型

1.2 模型参数辨识

在确定了电池的等效模型之后，需要根据电池的实际性能对模型中的参数进行辨识。这里需要辨识的参数有：UOC，R0，R1，C1，R2，C2。文章所使用的电池是一个由45块18650型三元电池并联组成的电池模块包，额定电压为3.6 V，额定容量为117 A·h。模型的参数辨识通过脉冲放电试验来实现，试验步骤为：在不同的SOC下，将电池以58.5 A电流恒流放电400 s后静置2 h，利用电池测试柜实时采集电池的电压和电流等动态参数。试验过程中电压和电流变化曲线，如图2所示。

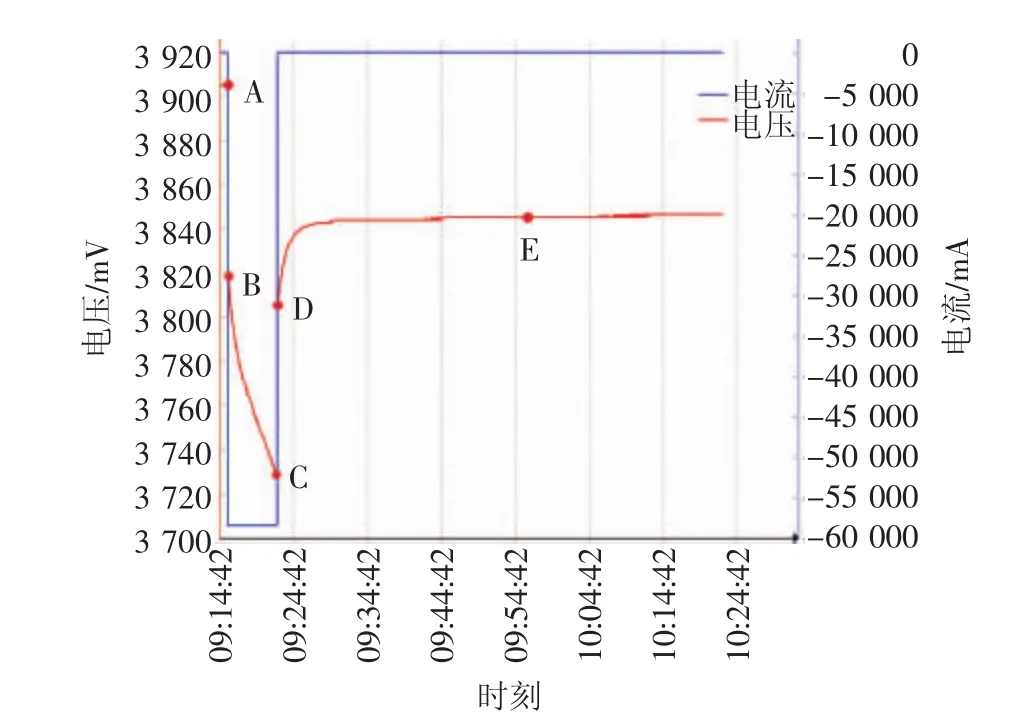
图2 脉冲放电试验中电流与电压的变化曲线

1.2.1 开路电压的辨识

在电池的充放电过程中，电池的SOC与电池电动势之间有一个相对稳定的对应关系。电池电动势的获取比较困难，而在电池长时间静置后，其内部的极化反应消失，此时其开路电压与电池的电动势近似相等，因此采用开路电压来代替电池电动势。通常测定“SOC-开路电压”关系采用的方法是选取不同的SOC点，测量电池充分静置后的开路电压，然而这种方法需要花费大量的时间。文献[1]提出了一种快速测量开路电压的方法，并对该方法的有效性进行了验证。试验步骤为：在某个SOC点，电流58.5 A放电10 s，静置40 s；电流58.5 A充电10 s，静置40 s，取2次静置40 s后电压的均值，即为当前SOC状态下的开路电压，再利用MATLAB软件对试验数据进行拟合，得到SOC-开路电压曲线，如图3所示。

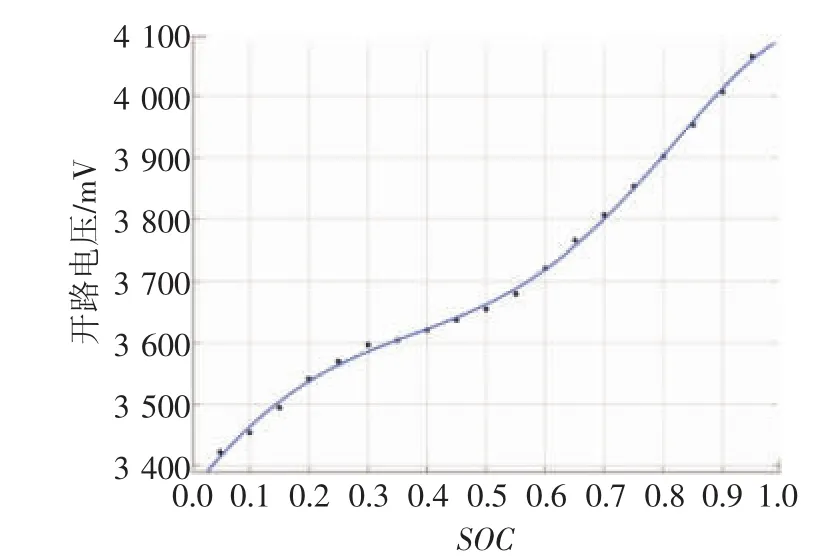
图3 SOC-开路电压拟合曲线

拟合所得公式，如式（1）所示。

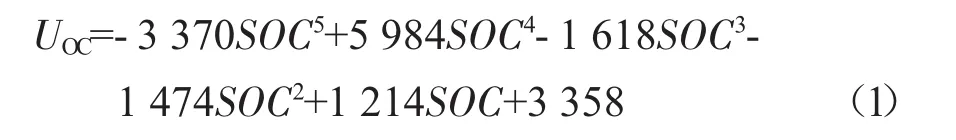
1.2.2 欧姆内阻及极化参数的辨识

在图2所示的放电过程中，放电开始和放电结束时电压有一个瞬间的直线下降过程，这是由电池的欧姆内阻（R0）引起的。利用这个特性计算电池的欧姆内阻，如式（2）所示。

式中：UA，UB——电池在图2中A，B点处的电压，mV。

由于电池开始放电前已经经过长时间的静置，其内部极化反应已经消失，故图2中A～C过程可以看作是电压的零状态响应过程。电池两端的电压，如式（3）所示。

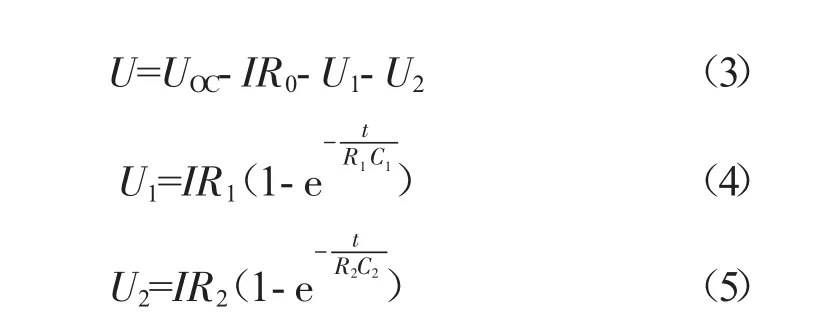
式中：e——常数，e=2.718 281 8…；

t——时间，s。

图2中，C～E过程是电池在放电后静置的过程，其电压变化过程可以看作是零输入响应过程，表达式如式（6）所示。

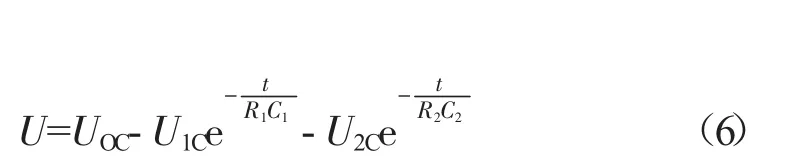
式中：U1C，U2C——电阻R1，R2在图2中C点处电压，mV。

令：

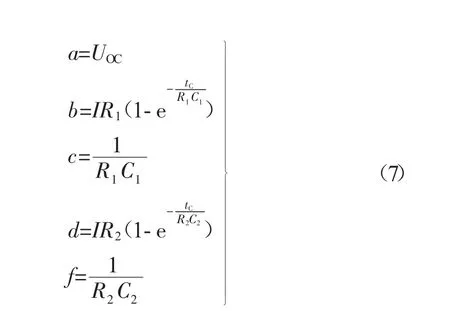
式中：tC——图2中C点处对应的时间，s。

则式（6）可以化简成：

然后利用MATLAB拟合工具，对图2中的DE曲线按照式（8）进行自定义公式拟合，得到 a，b，c，d，f的值，再根据式（7），即可得到 R1，R2，C1，C2的辨识结果。

最终 R0，R1，R2，C1，C2的辨识结果，如表 1 所示。

表1 2阶RC等效电路模型参数辨识结果

2 EKF估算电池SOC

EKF算法是对经典卡尔曼滤波器的扩展，将非线性系统的状态空间方程进行线性化处理，再利用卡尔曼滤波算法的递推过程对系统状态进行最优估算[2]。

2.1 EKF算法流程

EKF状态方程和输出方程，如式（9）所示[3]。

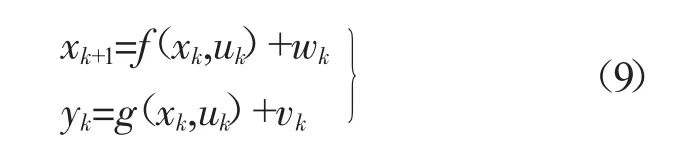
式中：xk+1，xk——系统的状态变量；

uk——控制函数；

yk——系统的观测变量；

f（xk,uk）——非线性状态转移函数；

g（xk,uk）——非线性测量函数；

wk，vk——k时刻的过程噪声、测量噪声。

根据图1，选取电池的SOC以及2个RC回路上的电压（U1，U2）作为电池的状态参数，并以I为输入量，U为输出量。则在电流激励下，各状态参数的关系，如式（10）所示。

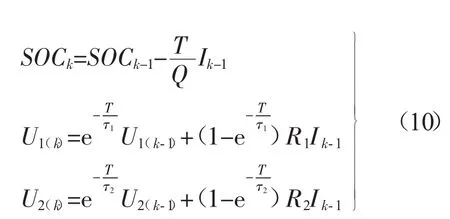
式中：T——采样周期，s；

Q——电池的额定容量，A·h；

τ1，τ2——R1C1环、R2C2环的时间常数，s；

U1（k），U2（k）——在k时刻电阻R1，R2两端的电压，mV。

令：xk=[SOCkU1（k）U2（k）]T，可将式（10）改写为：

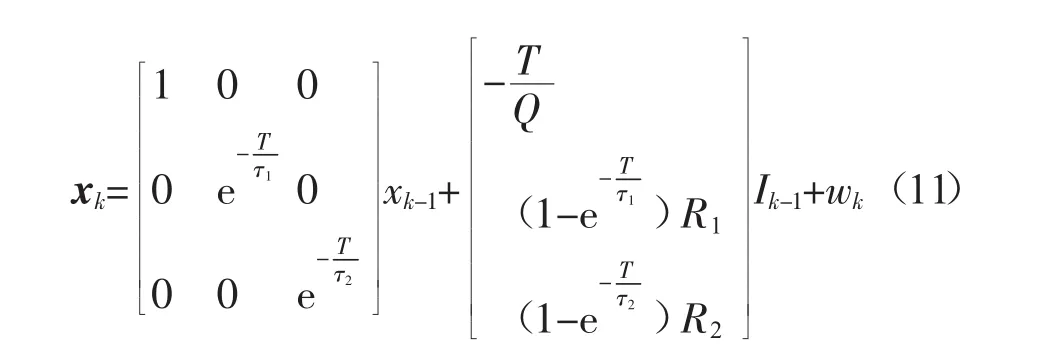
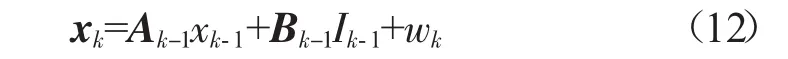
由电池等效电路模型得知，输出量（即电池两端电压U）与状态参数的关系，如式（13）所示。

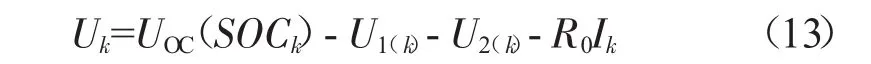
式中：Uk——k时刻电池两端电压，mV。

由1.2小节可知，UOC与SOC之间是非线性关系，因此UOC（SOCk）是非线性函数，根据EKF原理，对其进行线性化处理[4]：

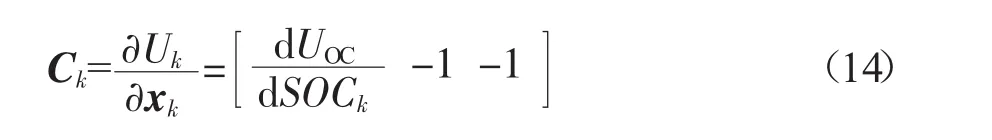
式中：Ck——雅克比矩阵。

令：yk=Uk，则电池模型的输出方程，如式（15）所示。

最后，利用EKF算法估算电池SOC的具体步骤如下：

1）为 xk、均方估计误差（Pk）、过程噪声方差（Qk）、观测噪声方差（Rk）设定初值。

2）根据前一时刻的状态估计值（xk-1）和均方误差估计值（Pk-1），对当前时刻的状态变量和协方差矩阵进行预估计：

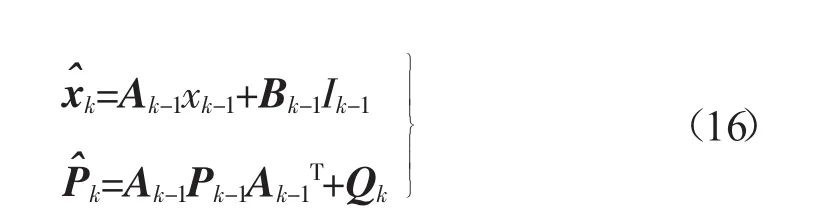
3）计算卡尔曼增益：

4）根据当前时刻的电压测量值（yk）和卡尔曼增益（Kk），修正状态估计值和均方差估计值，得到最优估计：

循环步骤2）～4）即可得到每个时刻的SOC值。

2.2 EKF算法估算SOC仿真

基于以上计算，在MATLAB/Simulink环境下搭建了SOC估算仿真模型，如图4所示。模型由参数估计、电池模型及EKF算法3个子系统组成，模型输入为电池工作电流，以当前时刻的SOC估计值作为下一时刻的输入，通过算法的不断迭代得到每一时刻的SOC最优估计，最后将仿真结果与SOC理论值对比来验证算法的准确度。

图4 EKF估算SOC仿真模型

图5示出仿真模型计算出的估计值和SOC理论值的对比，SOC的初值为0.8。为了验证EKF算法的有效性，将模型的初始SOC值分别设为0.85和0.75，仿真结果表明，EKF算法估算精度较高，并且不依赖于初值，对初始误差有很强的修正作用。

图5 EKF估算SOC仿真结果

3 结论

文章在Thevenin模型的基础上进行改进，建立了2阶RC等效电路模型，通过脉冲放电试验完成了电池内部参数的离线辨识，提高了电池模型的精确度；并将EKF算法应用在SOC的估算上，解决了传统安时积分法所带来的初始误差与累计误差的问题。该算法在提高SOC估算精度的同时，也提高了其可靠性。仿真结果表明，该算法具有较好的收敛性，在不同的SOC初值下都能够较快地收敛于真值。

文章建立的2阶RC等效电路模型参数是通过试验数据离线辨识得到，由于电池在工作过程中模型参数是实时变化的，因此通过离线方式辨识的模型参数并不一定能很好地跟踪模型真实值。可以通过在线辨识的方法来提高模型参数的准确度，从而建立更准确的电池模型，这也是下一步的研究工作之一。