纯电动汽车质心侧偏角估计及仿真分析*
方春杰
(重庆交通大学)

纯电动汽车(BEV)主动安全控制是其稳定性控制的主要发展方向,而质心侧偏角则是BEV主动安全控制过程的关键参数。尤其在高速移线和高速大转向等极限工况下,BEV质心侧偏角常被选作电子稳定控制(ESC)和四轮独立转向(4WIS)控制等主动安全控制系统的控制变量[1-2]。目前,BEV质心侧偏角无法通过传感器直接测量获得,需要根据相关车载传感器测量得到的转向盘转角、横摆角速度及侧向加速度等运动参量并采用估算算法进行估计,因而选取合适的质心侧偏角估计方法以及建立相应的状态观测器成为BEV主动安全控制的关键。文章以高速移线工况下的BEV为研究对象,建立3自由度车辆动力学模型,在CarSim中建立整车参数化模型,并采用MATLAB/Simulink搭建汽车驱动电机模型,基于扩展卡尔曼滤波(EKF)算法设计汽车质心侧偏角状态观测器,在ISO 3888紧急双移线工况下对状态观测器的估计效果进行联合仿真验证,以验证估计的准确性。
1 车辆动力学建模
1.1 车辆动力学模型
为了反映BEV在高速移线工况下的动力学特性,并为设计质心侧偏角状态观测器做铺垫,考虑车辆的侧向运动、横摆运动及侧倾运动,建立3自由度车辆动力学模型[3-5],该模型的动力学方程为:
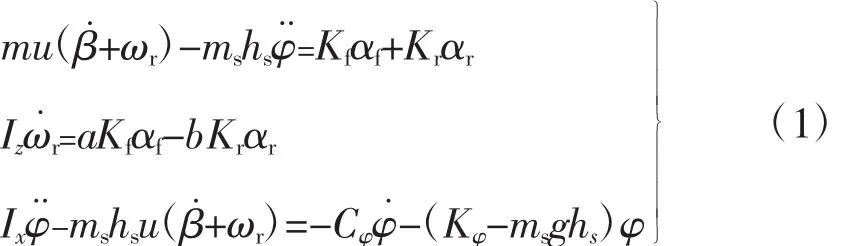
式中:m——整车质量,kg;
ms——簧载质量,kg;
u——纵向车速,m/s;
β——汽车质心侧偏角,rad;
ωr——汽车横摆角速度,rad/s;
a,b——汽车质心与前后轴之间的距离,m;
hs——汽车侧倾力臂,m;
Kf,Kr——前后轮轮胎侧偏刚度,N/rad;
αf,αr——前后轮轮胎侧偏角,rad;
Ix,Iz——汽车绕x,z轴的转动惯量,kg·m2;
φ——车身侧倾角,rad;
g——重力加速度,取9.8 m/s2;
Kφ——前后悬架总侧倾刚度,N·m/rad;
Cφ——前后悬架总侧倾阻尼,N·m·s/rad。
汽车前后轮轮胎侧偏角可表示为:

式中:Rf,Rr——前后轮侧倾转偏系数;
δ——汽车前轮转角,rad。
1.2 纯电动汽车整车参数化模型
为了得到实际的车辆运行状态参数及观测器所需的状态观测量,采用CarSim建立BEV整车参数化模型,根据文章研究的需要,对CarSim中的D级轿车部分参数进行适当调整,调整后的模型主要参数,如表1所示。
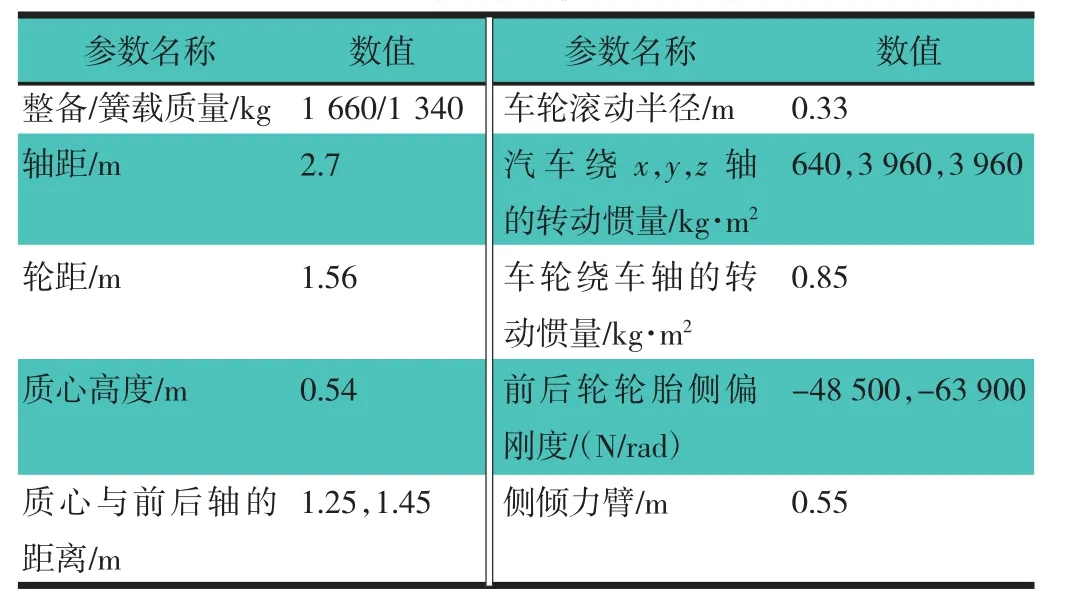
表1 整车参数化模型主要参数
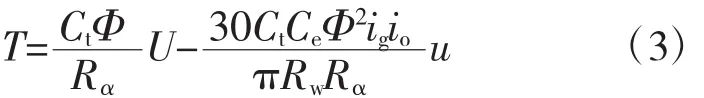
式中:T——驱动电机输出电磁转矩,N·m;
Ct,Ce——转矩系数和电动势系数;
ig,io——变速器和主减速器的传动比;
Φ——单个磁极磁通量,Wb;
Rα——电枢回路总电阻,Ω;
Rw——车轮滚动半径,m;
U——驱动电机端电压,V。
在MATLAB/Simulink中搭建BEV驱动电机模型,如图1所示。
1.3 驱动电机模型
由于CarSim中选用的D级轿车默认的动力源为传统的内燃机,而文章研究对象为BEV,因而需要利用外部的电机模型替换已有的内燃机模型[6]。采用理论建模法建立BEV驱动电机模型,其模型表达式[7]为:

图1 纯电动汽车驱动电机模型
2 汽车质心侧偏角估计
2.1 EKF算法
BEV稳定性控制系统是典型的非线性系统,因而选取的汽车质心侧偏角估计方法必须与该非线性系统相适应。EKF算法是一种适用于非线性系统的最小方差估计方法,该算法将非线性系统围绕状态估计值进行泰勒展开,并略去二阶以上高阶项,将非线性系统线性化,再利用卡尔曼滤波对线性化后的模型进行滤波处理[8]。EKF算法的具体实现过程如下。
非线性系统的状态方程和观测方程分别为:
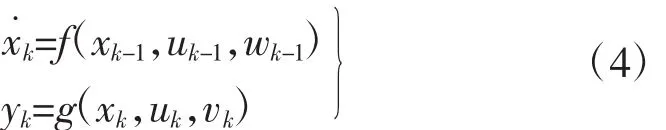
式中:xk-1,xk——系统实际的状态变量;
uk-1,uk——系统的输入变量;
wk-1,vk——系统的过程噪声和观测噪声;
f,g——系统的状态函数和观测函数;
yk——系统的输出变量。
2.1.1 预测过程
状态预测方程为:

误差协方差矩阵为:

式中:Pk-,Pk-1-——系统误差协方差矩阵的先验值;
A——g对状态变量x求偏导后的雅可比矩阵;
Qk-1——系统过程噪声协方差矩阵。
2.1.2 校正过程
EKF增益矩阵为:
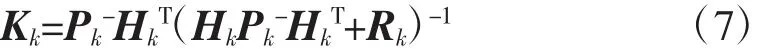
式中:Kk——EKF增益矩阵;
Hk——f对状态变量x求偏导后的雅可比矩阵;
Rk——系统测量噪声协方差矩阵。
EKF估计方程为:
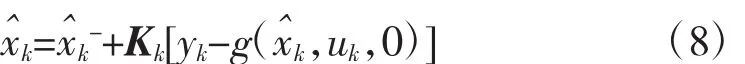

式中:Pk——系统误差协方差矩阵的当前值;
I——单位矩阵。
综上,可以得到EKF估计的具体过程,如图2所示。
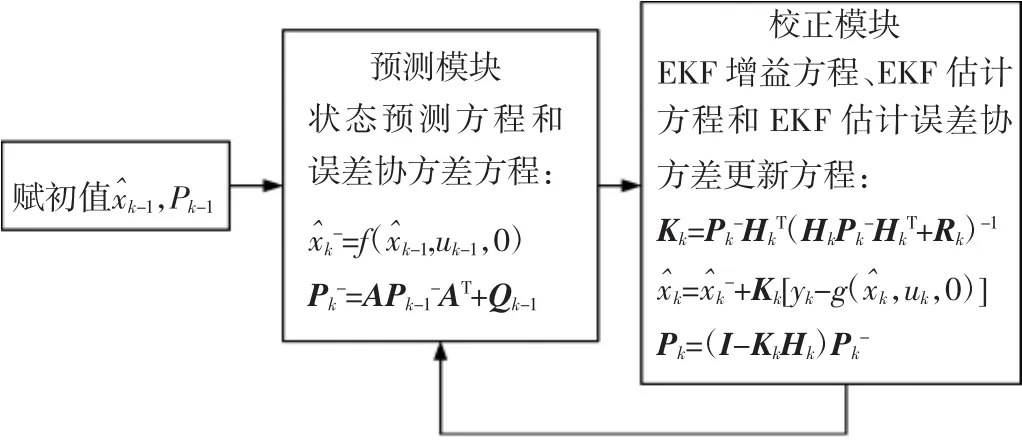
图2 扩展卡尔曼滤波(EKF)估计流程图
2.2 汽车质心侧偏角状态观测器设计
基于车辆动力学模型和EKF算法,设计BEV质心侧偏角状态观测器。根据式(1)和式(2),选取状态变量,输入变量 U(t)=(δ),输出变量 Y(t)=,将3自由度车辆动力学模型转化为状态空间形式,可以得到车辆质心侧偏角状态观测器的状态方程和观测方程为:

式中,各系数矩阵分别为:
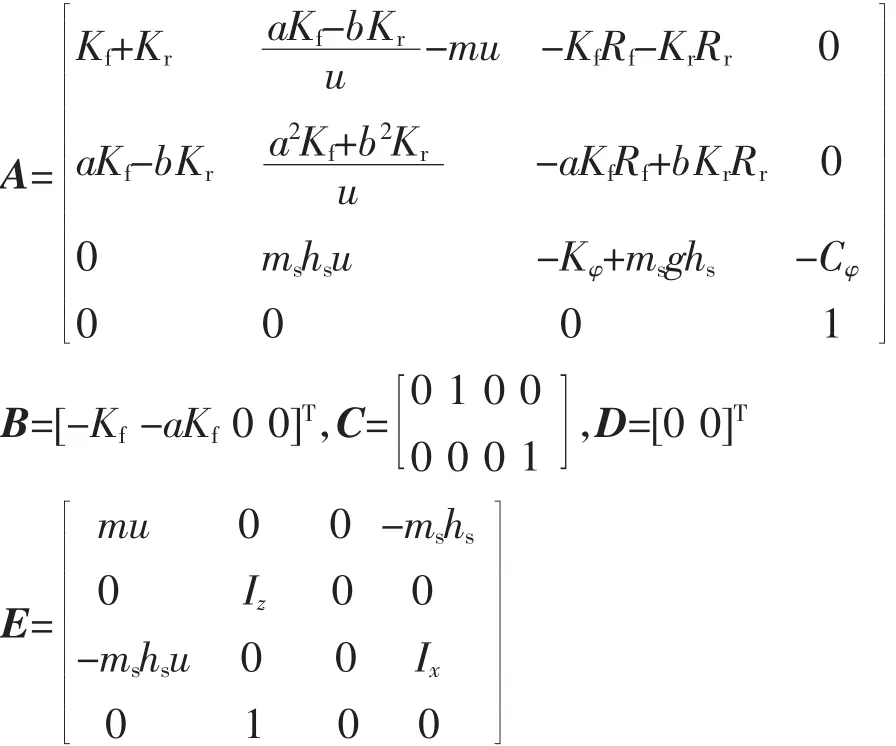
将式(10)代入图2所示的EKF估计流程中即可估算出BEV在相应运行工况下的质心侧偏角。
3 汽车质心侧偏角EKF估计仿真分析
ISO 3888紧急双移线工况是汽车操纵稳定性闭环控制研究中最典型的测试工况之一,设定汽车的初始速度为100 km/h,路面附着系数为0.8,仿真时间为10 s。该工况下的转向盘转角输入,如图3所示,CarSim整车参数化模型输出的观测量变化曲线(横摆角速度曲线、侧倾角速度曲线)分别如图4和图5所示。结合上述仿真条件,在ISO 3888紧急双移线工况下对BEV质心侧偏角EKF估计的效果进行仿真验证,得到仿真结果,如图6所示。

图3 汽车转向盘转角输入曲线
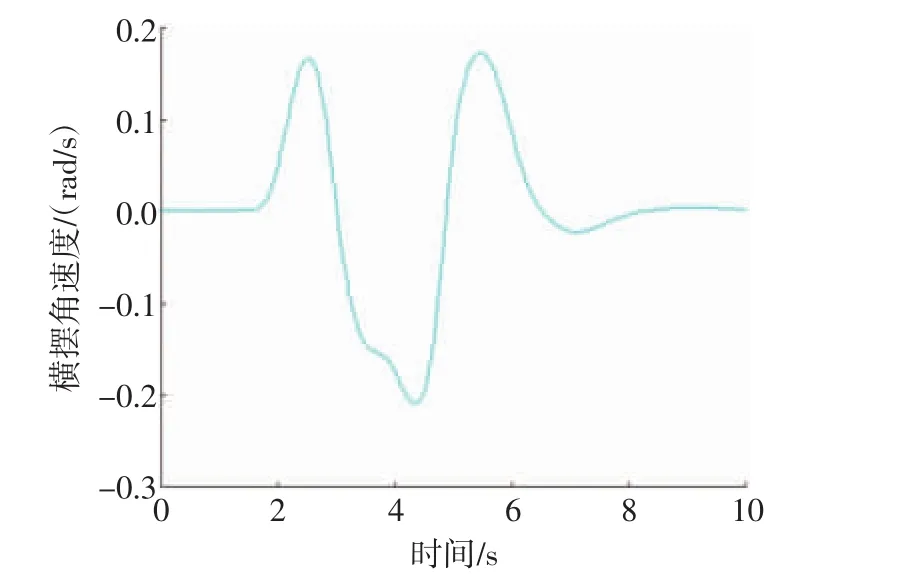
图4 汽车横摆角速度变化曲线
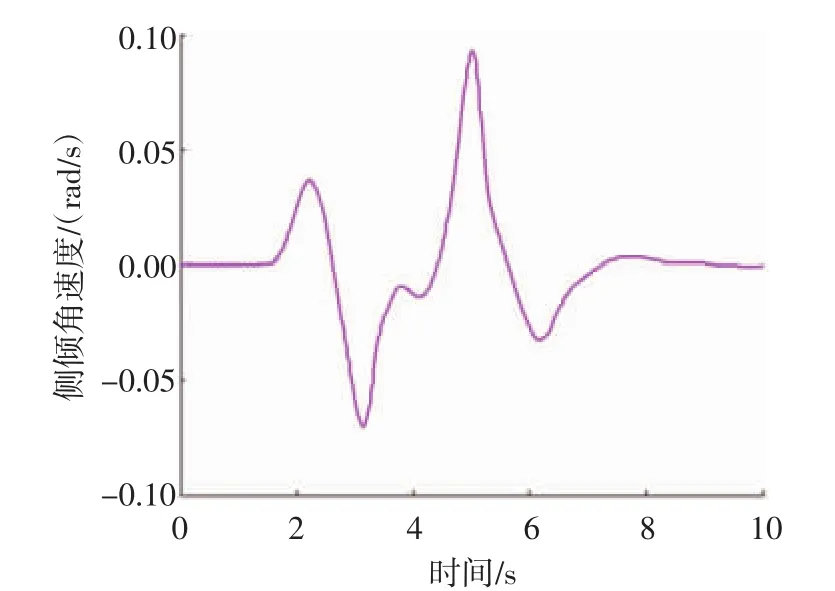
图5 车身侧倾角速度变化曲线

图6 汽车质心侧偏角变化曲线
从图6中可以看出,汽车质心侧偏角的实际值与估计值的变化趋势基本保持一致,两者之间绝对误差的较大值出现在曲线的波峰和波谷处,该处均为高速双移线中BEV发生较大转向处,汽车质心侧偏角在该处发生突变,因而实际值和估计值之间存在较大的绝对误差。整个仿真过程中,汽车质心侧偏角的实际值和估计值2条曲线基本吻合,两者的最大绝对误差为0.002 8 rad,低于允许出现的最大绝对误差阈值,且EKF估计的精度高达93.6%,达到了预期估计效果,能够满足ESC和4WIS控制等主动安全控制的实际需求。
4 结论
针对高速移线工况下的BEV,基于汽车动力学模型及EKF算法,设计了汽车质心侧偏角状态观测器,结合ISO 3888紧急双移线工况对汽车质心侧偏角状态观测器的估计效果与实际值进行对比仿真,仿真结果验证了BEV质心侧偏角EKF估计的准确性。ISO 3888紧急双移线工况下,汽车质心侧偏角状态观测器输出的估计值与CarSim整车参数化模型输出的实际值在曲线波峰和波谷处虽存在一定的偏差,但其大致趋势基本吻合,且估计精度较高,达到了预期估计目标,能够满足BEV稳定性控制系统的基本要求。

