基于联合仿真的汽车半主动悬架模糊控制分析

郝博然 卞学良 窦占峰 朱玉刚

（1.河北工业大学；2.中国汽车技术研究中心）

悬架的性能对汽车平顺性和操稳性影响显著。半主动悬架则可以根据不同路况改变阻尼或刚度的大小，性能较被动悬架有很大提升。和主动悬架相比，半主动悬架在性能接近的同时又具有安全性好、成本低及结构紧凑等优点。高性价比使得半主动悬架愈来愈受到国内外研究人员的关注。以往人们在对车辆动力学模型进行分析时，大多建立数学模型进行分析，而数学建模过程繁琐，利用软件搭建的数学模型可视化和可读性也较差，在一定程度上降低了工作效率和精度[1-3]。文章通过运用LMS.AMESim软件并基于物理意义对半主动悬架1/4车进行建模，建模思路清晰。然后利用MATLAB/Simulink设计了模糊控制器，对半主动悬架模型进行联合仿真，并对仿真结果进行分析，分析结果表明，采用模糊控制的半主动悬架较被动悬架性能有较为明显的改善，同时联合仿真的方法提高了工作效率和准确率，对半主动悬架的后续研究具有参考意义。

1 动力学模型分析

1.1 半主动悬架1/4车模型分析

汽车是一个复杂的振动系统，其振动形式和振动的影响因素繁多。但在研究不同问题时，可以在一些合理假设的基础上，将汽车简化为相应的简易模型进行分析。1/4车模型可以很好地反映垂直振动对汽车平顺性的影响，该模型能够仿真汽车乘坐舒适性、轮胎动载荷及悬架动行程[4-6]。半主动悬架1/4车模型，如图1所示。

图1 半主动悬架1/4车模型图

在该模型中，考虑了路面不平度输入、车身质量、轮胎质量、悬架的刚度和阻尼及轮胎刚度，忽略了轮胎阻尼的影响。根据牛顿运动定律，对车轮和车身进行动力学分析，得到微分方程组，如式（1）所示。

式中：m1，m2——轮胎质量和车身质量，kg；

q，z1，z2——路面不平度输入、轮胎垂直位移和车身垂直位移，m；

Kt——轮胎刚度，N/m；

K——悬架刚度，N/m；

C——半主动减振器的可变阻尼值，N/m·s；

C0——减振器基值阻尼，N/m·s；

CS——半主动减振器阻尼值的变化量，N/m·s。

通过节流口面积的变化，半主动悬架阻尼值可以相应改变，将减振器阻尼值设置为3档，分别实现阻尼的“软”、“中”及“硬”调节。模型的结构参数为：m1=35.85kg，m2=411.5kg，K=20200N/m，Kt=250000N/m，C0=1 600 N/m·s。

1.2 随机路面模型建立

通常情况下有2种方法产生随机路面不平度：1）白噪声信号通过滤波器作用产生滤波白噪声；2）白噪声信号通过积分器作用产生积分白噪声[7]。由于我国B级和C级路面占比重大，故选用谱密度为的积分白噪声信号来模拟C级随机路面，路面不平度（q（t）/m）的关系式，如式（2）所示。

式中：w（t）——白噪声信号，其均值为0；

n0——参考空间频率，m-1，此处n0=0.1；

Gq（n0）——路面不平度系数，m3，C级路面为256×10-6m3；

v——车速，m/s，此处v=20 m/s。

通过MATLAB/Simulink对C级路面模型进行仿真，仿真曲线，如图2所示。

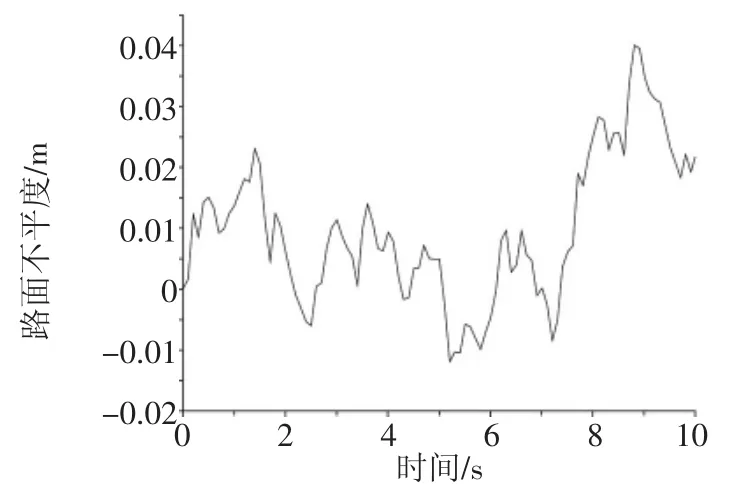
图2 C级随机路面仿真曲线图

2 模糊控制器的设计

模糊控制是智能控制的重要组成部分。模糊控制系统鲁棒性好，外界因素干扰和系统参数的改变对控制效果的影响较小，因此模糊控制对复杂的非线性时变系统尤为适合[8]。汽车悬架是一个复杂的非线性时变系统，选用模糊控制能够得到较为理想的控制效果。文章设计一个二维模糊控制器来实现对减振器阻尼的调节控制，实现半主动悬架阻尼值在“软”、“中”及“硬”三态切换。

2.1 模糊控制器结构

车辆悬架动挠度（z2-z1）与期望值0的差值设为偏差（E/m)；设为变化率（EC/（m/s）），将E和EC作为模糊控制器的输入变量，CS为输出变量。半主动悬架模糊控制流程，如图3所示。E和EC均采用7个模糊语言值：｛负大、负中、负小、零、正小、正中、正大｝，即｛NB，NM，NS，ZO，PS，PM，PB｝。模糊控制器输出量采用3个语言值｛软，中，硬｝，即｛S，M，H｝。

图3 半主动悬架模糊控制流程图

2.2 半主动悬架模糊控制器参数确定

2.2.1 基本论域

模糊控制器的输入和输出是和路面不平度输入紧密相关的。路面随机变化，输入量也会随机改变，因此应根据变化范围的最大值来确定基本论域[9]。通过仿真分析，确定了模糊控制器输入和输出量的基本论域。E和 EC 的基本论域分别为[-0.017，0.017]和[-3，3]；CS的基本论域为[-800,800]

2.2.2 模糊论域

将E和EC离散为13级，模糊论域为｛-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6｝。CS的模糊论域为｛-1，0，1｝，-1 对应阻尼负变化，此时减振器为“软”；0 对应减振器的软硬程度为“中”；1对应减振器阻尼变大，此时减振器为“硬”。

2.2.3 量化因子

在基本论域和模糊论域确定后，可以得到量化因 子 KE=6/0.017=352.94，KEC=6/3=2， 比 例 因 子KCS=800/1=800。

2.3 确定控制规则

设计模糊控制器的核心部分是确定模糊控制规则[10]。以悬架动行程及其变化率为输入量。设计控制规则的核心思想是：1）当悬架动挠度较大，且当变化量有增大的趋势时，应增大阻尼力以抑制动挠度的增大；2）当动挠度大，但其变化率使当前变化量有反向变化的趋势时，可减小阻尼值来减小车辆振动；3）当动挠度小，变化率小，应减小阻尼来衰减车辆振动[11]。在上述原则指导下，并结合大量仿真调试，制定模糊控制规则，如表1所示。输入量和输出量的隶属函数均选择三角形函数（Trimf），推理逻辑选择Mamdani法。

表1 模糊控制器控制规则表

3 AMESim和MATLAB联合仿真

3.1 仿真模型的建立

在AMESim的草图模式下，选择机械库和信号库中的部分元件，根据已建立的悬架动力学模型，搭建被动悬架1/4车模型和半主动悬架1/4车模型，如图4所示。并在模型中添加自定义接口Interface模块，实现与MATLAB/Simulink的通信，2个接口模块分别代表模糊控制器和路面，可为悬架模型提供控制器的输出阻尼和路面不平度输入。

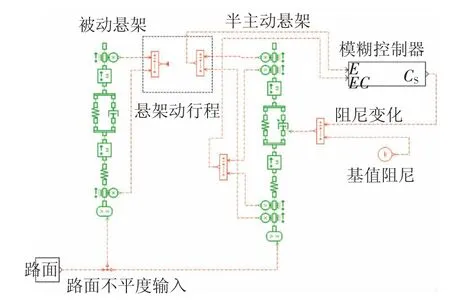
图4 AMESim悬架1/4车模型图

在MATLAB/Simulink操作界面，根据前面分析的设计结果，搭建路面输入和模糊控制器模型，如图5所示。图5中的悬架动力学模型为MATLAB中的S函数模块，它能够调用AMESim生成的执行文件，实现与AMESim的通信。悬架动挠度及其变化率经量化后传递给模糊控制器，经模糊推理后得出输出变量，乘以比例因子后再反馈给悬架模型，实现联合仿真。

图5 模糊控制器及路面输入模型图

3.2 仿真结果及分析

通过对被动悬架和半主动悬架的仿真分析，得到两者的车身垂直加速度对比图、车轮动载荷对比图及悬架动挠度对比图，如图6～图8所示。

图6 车身垂直振动加速度对比图

图7 悬架动挠度对比图

图8 车轮动载荷对比图

由图6～图8可以看出，当汽车以20 m/s的速度行驶在C级路面时，采用模糊控制的汽车车身垂直动加速度有较为明显的降低，悬架动挠度也有一定程度的降低，轮胎动载荷变化不大，悬架响应均方根值对比，如表2所示。

表2 悬架响应均方根值对比表

由表2可知，车身垂直振动加速度均方根值降低了13.30%，悬架动挠度均方根值降低了6.69%，车辆乘坐舒适性和操纵稳定性均得到了不同程度的改善；轮胎动载荷均方根值略有增加，增大3.66%，幅值增加3.39%，均增加不大，且在可承受范围之内，对车辆的影响可以忽略不计。因为车身垂直振动加速度、悬架动挠度及轮胎动载荷之间是相互制约相互影响的，一般只能改善其中1个或2个指标。综上，文章设计的模糊控制器设计合理，在本模糊控制策略控制下的半主动减振器性能较被动减振器有较为理想的改善。

4 结论

1）AMESim软件界面简洁，建模方便，省去了数学方程推导的繁琐过程，与MATLAB/Simulink联合仿真的方法可行有效。

2）文章设计的模糊控制器结构合理，控制规则有效，对半主动减振器具有良好的控制效果。车身垂直振动加速度和悬架动挠度得到改善，汽车乘坐舒适性和操纵稳定性得到提高。轮胎动载荷均方根值和幅值增加很小，影响甚微。所设计的控制器控制效果良好。