在游戏中探索策略
——“棋盘上的奥秘”教学实践与思考
□ 朱姗姗
在游戏中探索策略
——“棋盘上的奥秘”教学实践与思考
□ 朱姗姗
随着新一轮义务教育课程改革深入推进后,拓展性课程成为了热点话题。我们认为,数学拓展性课程,应该体现两个特征:第一,激发学生学习数学的兴趣;第二,激活学生思维,开发学生潜能。而以游戏为载体,发展学生的数学思维能力,应该是数学拓展性课程中的一种形式。
一、内容设计构想
在一次练习中,有一道习题引起了笔者注意:在8×8的棋盘右下角有一颗棋子,甲、乙两人轮流下棋,规定只能下在前一颗棋子的上面、左面或者左上方距离一格处,谁能用自己的棋子占领左上角谁就获胜,如果甲先下,那么谁会赢?
学生练习后,笔者在批改时发现,全班没有一位学生能够解决。经过交流发现,学生无法解决的原因有三:第一,部分学生不能理解题意,无法解题;第二,无法选择或有效使用“倒推”这一策略;第三,学生对必胜策略的寻找毫无头绪,无从下手。
究其原因,下棋是两个拥有理性思维的人之间的一种博弈,如果将这道题完全放给一个学生课后单独去做,没有两个人之间的对弈经验,学生很难从博弈角度去思考问题,思考也很难全面。
那么,这样的材料我们何不将其整理变形,构架一堂拓展课呢?笔者据此设计了“棋盘上的奥秘”这一数学拓展课课例。基本教学思路:第一,有师生对弈的引领,有生生对弈的探索以及三方讨论;第二,课堂中给予学生充分的对弈体验,让学生在与他人下棋的过程中,自主萌生博弈观念、倒推策略;第三,课程内容有一定的难度,因此,材料呈现循序渐进,环节推进张弛有度,逐步逼近学习目标。
二、教学内容
在“8×8”“8×8-5×5”的棋盘右下角放一颗棋子,以它为起点,两人轮流在这个棋盘上下棋,规定只能下在前一颗棋子的上面、左面或者左上方距离一格处,谁能用自己的棋子占领左上角谁就获胜。找出必胜策略。
三、教学目标
1.在下棋活动中学会用尝试验证和倒推的方法探索必胜策略。
2.在经历与他人博弈下棋的过程中,培养逻辑推理能力;尝试解释自己的思考过程,培养语言表达能力。
3.培养数学学习兴趣。
四、教学过程
(一)回顾微课内容,引出课程中心
在授课前一天,学生已在家观看微课“棋盘上的奥秘”,内容为:红红和明明两人在12×12的棋盘上下棋,规定从右下角开始,两人轮流下,且只能下在前一颗棋子左上方距离一格或两格处,谁先抢到左上角的点,谁就获胜。红红因抢到必胜点,三局都获胜。
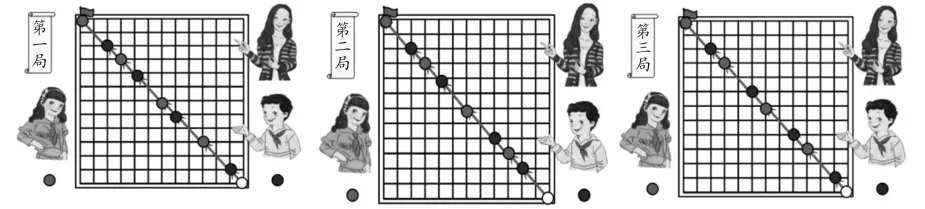
师:昨天看了微课,谁能告诉我,为什么红红三局都能赢?
生:因为红红抢到了3号点,在3号点上,不管对手下一格还是下两格,都能抢到终点。
师:像这样,不管对手如何下,都能保证必胜的点,我们叫它必胜点。师:想要下到这个必胜点,又得下到哪些点呢?生:想要下到3号点,我们必须抢到2号点,想要抢到2号点,必须抢到1号点。
师:我们用倒推的方法找出了所有的必胜点。所以在这个棋盘上,要后下,下必胜点,才能获胜。
【设计意图】这部分内容是整堂课的准备环节。有以下几个意图:①在微课中演示12×12的棋盘及根据相应的游戏规则的操作,便于学生熟悉棋盘,理解8×8棋盘的游戏规则;②引出在一维线上进行逆向推理的核心能力问题;③定义了必胜点并规范必胜策略的说法,使学生后续作答更具指向性。
(二)利用8×8的棋盘,在对弈中感悟尝试和倒推
1.理解规则。
展示题目:在8×8的棋盘上的右下角放一颗棋子,以它为起点,两人轮流在这个棋盘上下棋,规定只能下在前一颗棋子的上面、左面或者左上方距离一格处,谁能用自己的棋子占领左上角谁就获胜。

师:如果我的第一颗棋子下在这里,那么你的棋子可以下在哪里?
生:可以下在您的棋子的上面、左面或者左上方。
师生对弈,当教师下在距离终点2格处的点时,学生认输。
师:老师下到哪个点的时候,你觉得老师一定能赢,为什么?
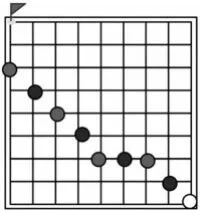
生:老师下到这个点时我觉得老师肯定赢了,因为我只能往上,老师就能抢到终点了。
【设计意图】因有12×12棋盘游戏的微课学习,学生对8×8的棋盘上的游戏规则比较容易理解。同时,师生对弈是为了保证全班学生都能掌握游戏规则,感知第一个必胜点,为下面找必胜点做铺垫。
2.探索必胜策略。
师:你想不想赢老师?给你时间探索赢老师的方法。
师布置任务:请同学们拿出练习纸,你可以和同桌对弈,下到哪个点的时候你觉得自己肯定能赢,把这样的点记录在必胜点记录区。
【设计意图】在这里,我们必须给予学生充分的对弈体验,在对弈中,让学生萌生博弈观念,倒推思路。
3.反馈。
(1)错误点
师:请找到这个点的同学来说一说是怎么想的。
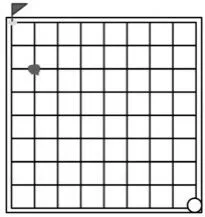
生:下到这个点,如果对手往上,我就可以往左上抢到终点;如果对手往左上,我就直接往上抢到终点。
生(反驳):下到这个点,如果对手往左,那么我就只能往上,这样终点就被对手抢到了,所以这个点不是必胜点。
(2)往下、往右倒推点
师:看来这个点不能保证我一定能赢,所以这个点不是必胜点,这个点呢?
生:如果我抢到这个点,对手就只能往上,我就能抢到终点。(见图1)

图1

图2
师:这位同学也找到了这个点,同时还找到了另一个点,你怎么想?(见图2)
生:如果我抢到这个点,对手就只能往左,我就能抢到终点。
(3)右下倒推点
师:你还发现哪个是必胜点,说说看。
生:这个点是必胜点,如果对方往左走,那我也往左,就可以抢到1号必胜点;如果对方往上,那我也往上,就可以抢到2号必胜点;如果对方往左上,那我也往左上,就直接抢到终点,也就是说只要我抢到这个点,不管对手往哪个方向下,我都能抢到终点。
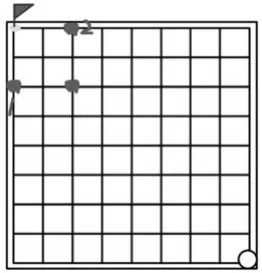
师:他说的让你明白了吗?谁能用自己的话再来说一说?
【设计意图】学生的对弈过程,实际上是一个试误的过程,不断地在各个点上尝试,然后发现:哪个点上不能保证一定能赢,哪个点上,不管对手怎么下一定能赢。这里的反馈分为三个层次,第一个层次,反馈错误点,让学生再次明确,下棋是一种博弈,在你想往对自己有利的方向发展时,对手也是这么想的,只有“不管对手如何下,都能保证必胜的点才是必胜点”;第二个层次,往右、往下的必胜点推导,为反馈右下必胜点做铺垫;第三个层次,右下必胜点推导,右下的必胜点的寻找稍有难度,通过多次复述的方式,让学生充分理解。
4.带领倒推。
师:那怎么才能抢到这个点呢?(见图3)
生:我觉得应该抢到这3个点(见图4),抢到1号点,对方往上,我也往上,就能抢到那个点;抢到2号点,对方往左,我也能抢到这个点;抢到3号点,对方往左我就能抢到1号点,对方往上,我就能抢到2号点,对方往左上,我就能直接抢到这个点。
生:我们已经知道,要抢到终点,必须抢到离终点两格的这3个点。现在,我们可以直接把这个点当成终点,就可以直接倒推出这3个点。
师:谁能像他这样来找一找能让我们抢到这个点的必胜点?(见图5)
生:和刚才一样,我们可以把这个点当成终点,那我必须抢到这3个必胜点。(见图6)
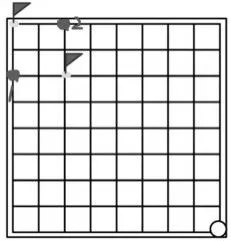
图3
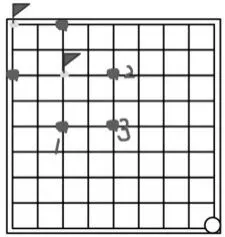
图4
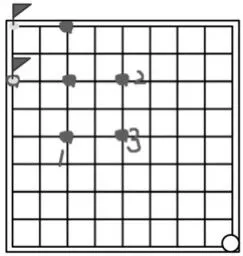
图5

图6
【设计意图】这一环节是基于学情的带领倒推,这里要反馈两种倒推方式:①边试误边倒推→对前一环节的再一次尝试和巩固;②建立模型后的倒推→类比倒推,建立模型,学会简化。
5.学生自主找必胜点。
师:你能像刚才那几位同学那样,找到所有的必胜点吗?试一试。
6.师生对弈2局均生赢。
师生对弈均生赢。
师:看来你已经找到必胜策略了。请把你找必胜点的过程,和同学们说一说。
生:想要抢到这个点,必须抢到这个点;想要抢到这个点必须抢到这个点;想要抢到这个点必须抢到这个点……(见图7)
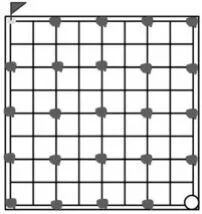
图7
师:他刚才是在干吗?
生:从终点开始往起点倒推。
师:所以必胜策略是?
生:先走,走必胜点。
【设计意图】学生赢了教师,受到了极大鼓舞,获得了数学学习的成就感。此环节注意引导:想要抢到这个点,必须抢到这个点;想要抢到这个点,必须抢到这个点……通过语言规范,领悟“倒推”原理。
7.小结。
师:回顾一下,为了找到这个棋盘上的必胜策略,我们先做了什么,又做了什么?
生:先尝试,找出离终点最近的3个必胜点,再从终点开始,往起点倒推。
师:同学们,我们通过倒推的方法找完必胜点之后,老师和这位同学对弈,其实就是在验证大家的必胜策略是否正确。(板书:验证)
【设计意图】回顾解决问题的全过程,并告知学生:必胜策略找到后的对弈其实是一种验证,使解决问题的过程更完整。
(三)出示8×8-5×5棋盘,引发认知冲突
1.自行找必胜点。
师:把两个棋盘放在一起呢?请你独立思考,找出必胜策略。
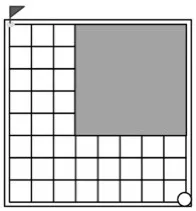
2.反馈。
生:想要抢到这个点,必须抢到这个点;想要抢到这个点必须抢到这个点;想要抢到这个点必须抢到这个点……所以必胜策略是先走,走必胜点。(见图8)
师:我们来验证一下。(生黑棋先走,师白棋后走)(见图9)
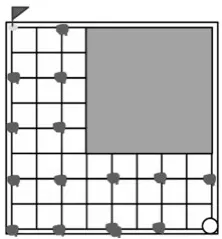
图8
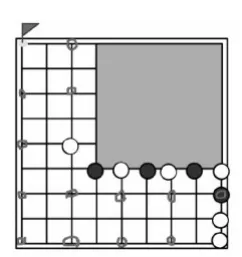
图9
师:你不是已经找到必胜点了吗?为什么还会输?
生:必胜策略有误。
师:我们用验证的方法发现,我们的必胜策略是有漏洞的。老师下到哪个点的时候你觉得必胜策略可能是有漏洞的?
生:没考虑老师往上走。
师:看来我们认为的必胜点,还存在着漏洞,说明我们在倒推的过程中必须考虑对手的各种可能性,让自己的思维更严谨、更全面。(板书:严谨、全面)。那么真正的必胜点在哪儿呢?
【设计意图】学习了前面的知识,学生会产生思维定势,以为只要进行“田”字倒推即可,这一环节让学生产生了强烈的认知冲突,从而促进学生反思:①得出必胜策略后要进行验证;②倒推时务必严密思维。这一环节,既让学生体验了反思的意义,又让学生感受到完整的解决问题的过程。
(四)回顾所学,全课小结
师:在今天这堂课上,你有什么新的收获?
生:在寻找策略的时候我们可以先尝试一下,找找感觉。
生:学会用倒推的方法去解决数学和生活问题。
生:思考问题要严密。
生:倒推后的顺向验证能帮我们验证倒退结果是否真的正确。
五、教学反思
(一)关于材料
本课例,采用学生十分喜爱的下棋游戏,学生兴趣高涨,求知欲强烈。从8×8到8×8-5×5,棋盘在不断地演变,学生也在层次不断递进的材料引导下,触碰他们的“最近发展区”,从原来的没有一个学生能够解决问题,到最后的几乎每个学生都至少能够解决8×8的棋盘,不同程度的学生有不同层次的收获。
(二)关于过程
在课堂上,教师放手让学生通过不断的试误,在尝试中进行自我纠错、反思和辨正,在量变下慢慢积累经验最后“顿悟”质变,让学生自发地去寻找解决问题的策略,有了最深刻的体验。
让教学中的每一个设计,都有效服务于学生的成长。整堂课的每一个过程设计都有教师的设计意图、细化目标。尽管材料不断演变,但本课例的每一个材料都紧紧围绕“博弈”“倒推”展开,将最大的力气用在培养学生的推理能力上。
(三)关于内容的延伸
授课后,我们也一直在思考棋盘的材料是否有更多可挖掘和探索的地方。如将规则改成只能往上或往左走,那么必胜策略会怎样?这时候必胜策略的得出,除了可以在棋盘上倒推,还可以将棋盘上的路线拉成一根能走17步的线段,那么这时候棋盘就和抢数游戏完全相通了,方法和策略也在不同的材料中延伸贯通了,看来很多数学游戏可以成为我们开发的资源。
(浙江省杭州采荷第一小学教育集团 310000)

