算式与情境的辩证关系
□ 郜舒竹
专题研究
算式与情境的辩证关系
□ 郜舒竹
在小学数学课程的教学中,常见的模式是首先出示一个有故事情境的问题,而后画出示意图直观显现出数量关系,在此基础上列出算式并计算,进而获得问题答案。将这种“从情境到算式”单一的学习活动,拓展到情境与算式相互联想的学习活动。对于加法和减法算式,背后的情境类型主要包括:局部与整体的关系、不同对象比较的关系以及运动与变化中的关系。
算式 情境 辩证关系
在小学数学课程的教学中,常见的模式是首先出示一个有故事情境的问题,比如:
笑笑有5个红色的玻璃球和3个蓝色的玻璃球。她一共有多少个玻璃球?
而后画出示意图,直观显现出两个局部构成一个整体的数量关系(见图1)。

图1 局部与整体示意图
在此基础上列出算式并计算:5+3=8,从而得到问题的答案为:笑笑一共有8个玻璃球。
在这样的过程中,学生所经历的学习活动主要包括两个转换,第一个转换是通过对文字表述的情境性问题进行理解,并将文字叙述转换为直观的图形;第二个转换是将数量关系用算式表示出来,并通过计算得到答案。这样的思考过程可以称之为“从情境到算式”的学习活动。如果把这个过程反过来,让学生经历从“算式到情境”的思考过程,其中就会蕴含更丰富的思维活动。这种反过来的学习活动可以称之为“给算式讲故事”。
一、给算式讲故事
按照辩证唯物主义对立统一的观点,应当相信任何过程都有其相反的过程存在,比如有“前进”的过程,就会有“倒退”的过程。有上升的过程,就会有下降的过程。数学的学习有“从情境到算式”的思考过程(见图2)。

图2 “从情境到算式”示意图
那么,就应当伴随有反过来的“从算式到情境”的过程(见图3)。

图3 “从算式到情境”示意图
如果把“从情境到算式”的思考过程理解为“为问题找答案”,那么反过来“从算式到情境”的思考就是“为算式找应用”。如果把情境看作是现实世界中的问题,把算式看作数学中的抽象模型,这样的思路反映的就是现实世界中的具体问题与数学中抽象模型相互作用、互为因果的辩证关系。
从情境到算式,其结果通常是确定的,而从算式到情境就具有相当广泛的开放性或者多样性。比如针对“5+3=?”这样的加法算式,可以引导学生用“为算式讲故事”的方式,去思考什么情况下可以使用这样的算式。
最为常见的一种情况就是前面问题中的数量关系,即一个整体由两个局部组成,其基本关系可以用图4表示出来。

图4 整体与局部关系示意图
如果已知两个局部的数量,则运用加法可以计算出整体的数量。与之对应的减法问题就是知道整体和一个局部的数量,求另外一个局部的数量(见图5)。

图5 已知整体求局部示意图
用文字叙述这个问题可以是:笑笑有8个玻璃球,5个是红色的,其余是蓝色的。她有多少个蓝色的玻璃球?
这种整体与局部关系的情境应当说相对简单,较为复杂并且对于低龄儿童不易理解的,还有不同对象间进行比较的数量关系。
二、比较的关系
比较关系的故事情境通常需要有两个对象,各自的数量不同,因此就会出现“多多少”或者“少多少”的问题。比如对于“5+3=?”就可以叙述出情境性问题。
(1)淘气有5个玻璃球,笑笑比他多3个。笑笑有多少个玻璃球?
(2)淘气有5个玻璃球,如果笑笑减少3个就和淘气一样多。笑笑有多少个玻璃球?
对应的示意图可以是图6的形式。

图6 “多多少”示意图
还可以交换主语和宾语的位置叙述。
(1)淘气有5个玻璃球,比笑笑少3个。笑笑有多少个玻璃球?
(2)淘气有5个玻璃球,如果他再增加3个就和笑笑一样多。笑笑有多少个玻璃球?
这两种文字叙述的关系可以用图7表示出来。

图7 “少多少”示意图
鉴于加法和减法的互逆关系,从这些加法算式的情境,还可以衍生出用减法算式计算的故事情境,为了清晰起见,这些问题和相关的示意图,罗列在表1中。
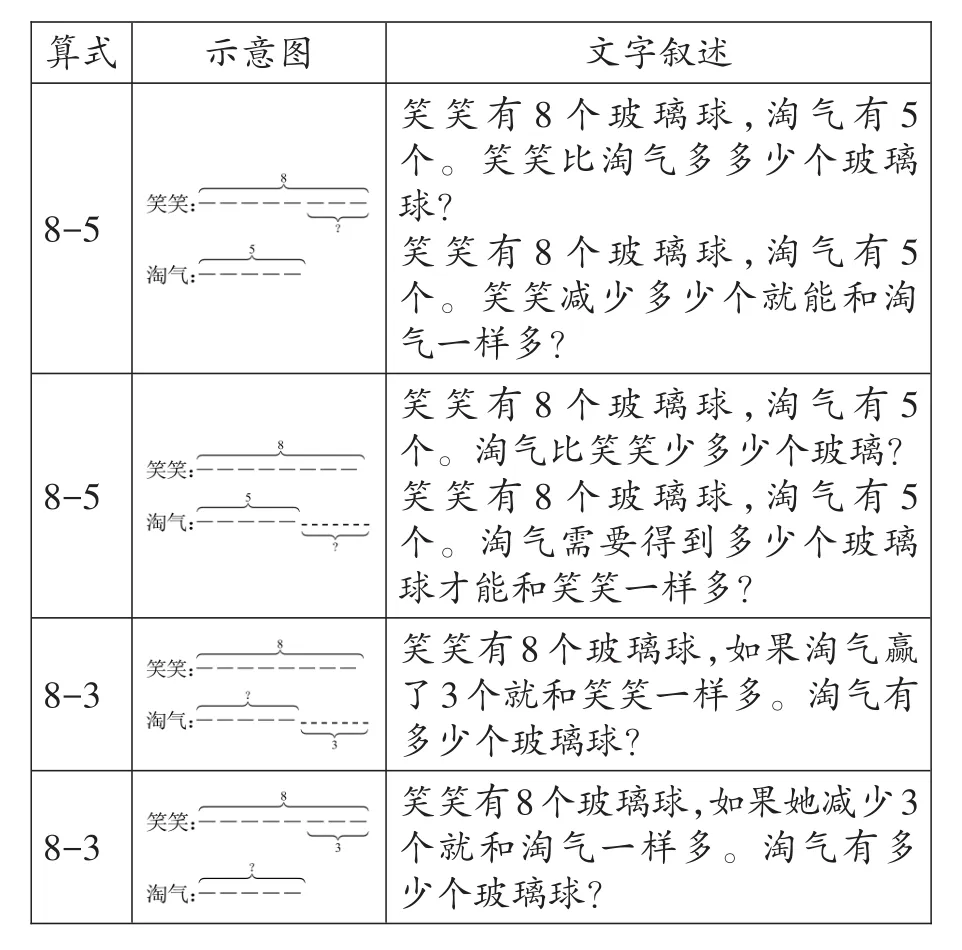
表1 比较关系减法情境问题
对于低龄儿童,这些问题的困难往往不是数学中的计算,而是对用语言或者图形表示出来的故事情境难以理解。“给算式讲故事”这样的学习活动能够帮助学生熟悉各种各样的情境,以及与算式的对应关系。对于加法算式,除了以上介绍的局部与整体关系和不同对象比较关系的情境,还有体现数学中的变换思想,也就是运动与变化中各种关系的情境。
三、运动与变化中的关系
运动与变化的情境往往表现为同一人物或对象,在不同时间或者地点的不同状态。比如:
笑笑有5个玻璃球,淘气又给了她3个。笑笑现在一共有多少个玻璃球?
情境中的人物笑笑经历了变化前有5个玻璃球,变化中又得到了3个,变化后一共是8个的过程。这一变化过程可以用图8表示出来。

图8 变化示意图
这样的运动与变化的过程,有可能是增加,也有可能是减少。如果变化过程是“增加”,那么“5+ 3=?”对应的问题就应当是图9所示求变化后的问题类型。

图9 求变化后示意图
用文字叙述出来就是:笑笑有5个玻璃球,淘气又给了她3个。笑笑一共有多少个玻璃球?
如果变化过程是“减少”,那么“5+3=?”对应的问题就应当是求“变化前”的数量(见图10)。

图10 求变化前示意图
用文字可以叙述为:笑笑有一些玻璃球,给了淘气3个后还剩5个。笑笑原来有多少个玻璃球?
此类问题也可以衍生出“8-5=?”以及“8-3=?”的情境性问题(见表2)。

表2 减法算式情境性问题
用运动与变化的眼光看算式,可以联想出许多现实性的故事情境。比如城市交通中的“公交车”,如果车上原有3名乘客,到站后又上来4人,现在就有“3+4=7(人)”(见图11)。

图11 公交车情境示意图
学生在低年级时熟悉这种运动与变化的情境,对今后的学习是非常有益的。比如认识负数,因为负数描述的是与正数意义相反的量,因此认识负数就需要理解什么是相反意义的量。对于运动与变化的故事情境,这种正与反的关系通常会比较明显。比如“公交车”情境中,有上车的乘客,也有下车的乘客,那么如果用“正”表示上车的人数,那么“负”就表示下车的人数。
再比如,一只乌龟向前走了5步,而后又倒退了9步。那么这里的5步和9步就具有了方向相反的意义(见图12)。

图12 乌龟前进与倒退示意图
把这种相反方向的变化过程进一步推广,就可以引申为高中数学课程中对向量概念的认识。所谓向量在数学中就是给一个数赋予方向的含义。比如,对于一个运动的情境:某人从A出发,向东行走4千米到B。之后又向北行走3千米到C(见图13)。

图13 向量加法
这里的数字4和3不仅有表示多少千米的含义,还有“向东”和“向北”不同方向的含义。这时对于算式“4+3”就不能简单地计算答案等于7,而要根据具体情境中的问题目标而决定。如果问“一共行走多少千米”,可以直接利用算式“4+3”进行计算得到结果为7千米。但是如果问“起点与终点最短距离是多少千米”就不能这样计算了,需要用向量加法的法则计算出结果为5千米,这个计算需要运用初中数学的勾股定理。
用运动与变化的眼光看算式,实质上是将算术运算与几何中的变换联系起来。比如在图14中一个形体初始位置在数轴上“3”的位置,加4后就变换到“7”的位置。这个加法运算就描述了几何变换中的平移。
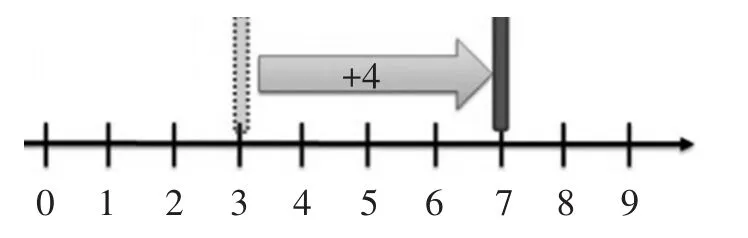
图14 平移变换示意图
总之,将“从情境到算式”单一的学习活动,拓展到情境与算式相互联想的学习活动,可以更加全面地认识情境与算式的辩证关系,让学生经历的不仅是解决问题的过程,还包括了对同一算式对应不同情境的认识,实质上是开拓了学习活动设计的思路,为变教为学课堂教学改革中的学习活动增加了更为丰富的内容,同时也为今后的数学学习奠定了更为坚实的基础。
[1]Thomas A.Romberg,Kevin F.Collis and Douglas A.Grouws.Learning to Add and Subtract. Journal for Research in Mathematics Education. Monograph,Vol.2,Learning to Add and Subtract (1987),pp.i+vii-viii+1-178.Published by:National Council of Teachers of Mathematics.
[2]F.J.Van Den Brink.Numbers in Contextual Frame Works.Educational Studies in Mathematics, Vol.15,No.3(Aug.,1984),pp.239-257.Published by:Springer.
[3]Patrick W.Thompson and Tommy Dreyfus. Integers as Transformations.Journal for Research in Mathematics Education,Vol.19,No.2(Mar.,1988), pp.115-133.
(首都师范大学初等教育学院 100048)

2016年北京市科技计划面上项目“数学的教育形态研究”(KM201610028020)

