钢筋混凝土梁表面裂缝与其力学行为的分形研究
宋 琨 于广明 周福强 谢焦焦
(青岛理工大学土木工程学院 山东 青岛 266033)
钢筋混凝土梁表面裂缝与其力学行为的分形研究
宋 琨 于广明 周福强 谢焦焦
(青岛理工大学土木工程学院 山东 青岛 266033)
通过钢筋混凝土梁四点受弯试验,验证了混凝土梁表面裂缝具有统计意义上的自相似分形特性,进而研究了不同外荷载作用下,钢筋混凝土梁表面裂缝发展分布及其分形维数变化的规律。通过钢筋表面粘贴应变片的方法计算出不同外荷载下钢筋的最大应力,绘制分级荷载下钢筋混凝土梁裂缝的分形维数与钢筋最大应力的拟合曲线,得出钢筋最大应力与混凝土梁表面裂缝分形维数的关系,为实际工程中评估构件破坏程度提供了参考价值。
混凝土;裂缝;分形;应力
一、引言
Mandelbrot创立的分形理论[1],打破了人们以欧式几何方法去认识世界的局限性,从而改变了人们的思维,为研究自然界中复杂且不规则的系统提供了一种定量描述手段。分形理论使事物在极端有序和极其混沌的关系之间提供了一种可能,从而可以在复杂的自然现象中找到其发生发展的规律[2-5]。
钢筋混凝土梁在受力过程中会在其表面产生裂缝并随着荷载的变化而不断扩展,通过对钢筋混凝土梁裂缝的研究可知,梁表面的裂缝具有很明显的分形特性[6],因此可以采用改变观察尺度的方法来计算出各级荷载下梁表面裂缝的分形维数,并根据各级荷载下钢筋表面应变片的读数计算出相应的钢筋最大应力,从而建立裂缝的分形维数与钢筋最大应力的关系,为混凝土结构的损伤评估提供理论依据。
二、钢筋混凝土梁受弯试验
该试验梁构件采用单筋矩形截面,在受拉区布置两根边长为16mm的方形钢筋,在上部布置两根直径为6mm的一级光圆钢筋作为架立筋,试验梁的截面尺寸选为b×h=248mm×296mm,梁长2.7m,左右支座距梁端各为150mm,梁的计算跨度取2.4m。试验梁所用混凝土强度为C30,抗压强度设计值为fc=14.3N/mm2,抗拉强度设计值为ft=1.43N/mm2,弹性模量Ec=3.0×104N/mm2。试验所用钢筋为HRB335,强度设计值fy=300N/mm2,强度标准值fyck=335N/mm2,弹性模量为Es=2.0×105N/mm2,混凝土保护层c=32mm。试验时预加荷载5kN,以后每步递增5kN直至梁完全破坏。
在试验中,为了得到钢筋和混凝土的应变值,在钢筋表面及混凝土下表面粘贴应变片来计算钢筋及混凝土的变形。
三、梁表面裂缝发展分布的分形规律
(一)钢筋混凝土梁表面裂缝的发展
该实验中,从钢筋混凝土梁开始出现裂缝时对裂缝分布进行记录,详细描述试验过程中钢筋混凝土梁随外部荷载变化的裂缝发展分布情况,并对各级荷载作用下的裂缝分布进行绘制
(二)钢筋混凝土梁裂缝分布的分形维数
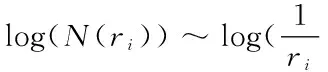
为计算方便,本文用FractalFox程序对钢筋混凝土梁表面裂缝的分形维数进行计算。如图4所示,FractalFox程序可以对直接导入的裂缝图片进行网格划分,并自动记录不同盒子尺寸下的盒子数,然后对结果进行对数计算并拟合出双对数曲线,则图中曲线斜率的绝对值即为所计算荷载下裂缝的分形维数。
在试验荷载达到40kN时,梁表面开始出现微小裂缝,随着外荷载的继续增加,裂缝逐渐发展,当外荷载达到110kN时,钢筋混凝土梁破坏。当外荷载小于50kN时,梁表面裂缝的分形维数小于1,说明裂缝在扩展初期,并不具备统计意义上的自相似性。当外荷载达到50kN时,裂缝发展逐渐加快,裂缝的分布状态也更加复杂,其分形维数也大于1,通过对盒子尺寸和盒子数的双对数曲线的线性拟合,其相关程度也达到了90%以上,可认为其已经具有了统计意义上的自相似性。随着外荷载的增大,裂缝发育逐渐饱满,分形维数也在逐渐增大,进一步证明了采用分形几何理论研究混凝土裂缝的可行性。
四、分形维数与钢筋最大应力的关系
当外荷载达到50kN时,随着外荷载的不断增大,裂缝分形维数也在不断增大。根据表2中所列出的梁的应变数据可以看出,随着外荷载不断增大,梁的应变也在逐渐增大,计算钢筋最大应力时取跨中处的应变来计算。将不同外荷载下钢筋混凝土梁表面裂缝的分形维数D和钢筋的最大应力σmax进行拟合,可以得到裂缝的分形维数—钢筋的最大应力的回归关系曲线如下:
σmax=15702D2-34203D+18761
(1)
式中,σmax为钢筋的最大应力;D为裂缝的分形维数。
从图1可以看出,裂缝的分形维数—钢筋的最大应力有着很好的拟合度,因此对于钢筋混凝土构件来讲,钢筋的最大应力与裂缝的分形维数可以用二次多项式进行拟合。因此可以利用这一关系,通过测量钢筋混凝土梁表面裂缝的分形维数来估算梁内钢筋的应力,进而评估混凝土梁构件内部的损伤程度。
五、结论
本文利用钢筋混凝土梁四点受弯试验,验证了钢筋混凝土梁在承受外荷载作用下其表面裂缝的发展分布具有统计意义上的自相似分形性质,研究了钢筋混凝土梁在随着外部荷载增加的过程中,内部钢筋最大应力与梁表面裂缝的分形维数之间的定量关系,因此可以利用裂缝的分形维数来表征裂缝发展分布的规律。在试验梁表面裂缝逐渐变化发展的过程中,裂缝的分形维数以及梁内钢筋的应力也在随之变化,因此可以利用梁表面裂缝的分形维数来评估梁的受力状况以及破坏程度。
[1]Mandelbrot B B.The Fractal Geometry of Nature.San Francisco[J].W.H.Freeman and Company,1982:361-366.
[2]辛厚文.分形理论及其应用[M].合肥:中国科学技术大学出版社,1993.
[3]Xie H P.Fractals in Rock Mechanics[M].Netherlands:A.A.Balkema Publishers,1933.
[4]特科特D L.分形与混沌-在地质学与物理学中的应用.郑捷,季颖译.北京:地震出版社,1993.
[5]O Z.M N.M B.Fractal-Cantorian geometry,Hausdorff dimension and the fundamental laws of physics[J].Chaos,Solitons and Fractals.2003(1):113-119.
[6]李士彬,汤红卫,朱慈勉.钢筋混凝土构件损伤演化的分形行为[J].石家庄铁道学院学报,2006,(01):54-57+66.
[7]朱华,姬翠翠.分形理论及其应用.[M].北京:科学出版社,2011.
宋琨(1990.01-),男,汉族,河北省晋州市,硕士研究生,青岛理工大学,结构工程。

