浅谈数学家高斯的贡献

万忠义 周小义

(1.成都理工大学管理科学学院 四川 成都 610059;2.四川省安岳县乾龙九义校 四川 安岳 642350)



浅谈数学家高斯的贡献

万忠义1周小义2

(1.成都理工大学管理科学学院 四川 成都 610059;2.四川省安岳县乾龙九义校 四川 安岳 642350)

18世纪德国著名的一个伟人约翰·卡尔·弗里德里希·高斯，他是历史上最伟大的数学家之一。他的一生在不同的领域都为人类做出了伟大的贡献，本文主要目的是解读数学家高斯，从高斯的生活背景，高斯在数学方面的贡献，以及高斯为后人带来的影响作为重点，对伟大的数学家高斯进行较为详细的解读。

高斯；数学家；贡献；影响

一、引言

高斯的全名是约翰·卡尔·弗里德里希·高斯，是德国著名的数学家，物理学家，天文学家和大地测量学家。在很多方面都为人们做出了伟大贡献，在数学方面，几乎遍及了数学的各个领域，在物理方面，磁场上的巨大贡献，以及在天文、大地测量上都做出了巨大的贡献。他出生平凡却不平庸。凭着自己的聪明才智，勤奋努力的学习，刻苦的专研，终于成为了数学史上的传奇人物，并享有“数学王子”的美名，他与阿基米德、牛顿、欧拉齐名，被称为历史上最伟大的数学家之一。

二、高斯在数学上的成就

(一)二次互逆定理

“二次互逆定理”非常漂亮的解决了勒让德符号的计算问题，从而在实际问题上解决了二次剩余的判别问题。1796年，高斯作为世界上第一个严格的证明“二次互逆定理”的人，在此之后他又发现了这种定理的另外七种不同证明方法。高斯把二次互逆定理看作是算术理论中的宝石，是一个黄金定律。有人说：“二次互逆定理是数论中最重要的工具，并且在数论的发展史中，处于中心地位。”

在高斯之后柯西、克罗内克、雅克比、刘维尔、弗洛比纽斯等等也一个个地给出了新的证明方法。时至今日，二次互逆定理已经有了一百五十种不同的证明方法。二次互反律可以推广到高次互反律。二次互反律被称为“数论之母”，在数论中有着极高的地位。表述如下：

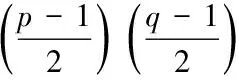
后来希尔伯特、塞尔等数学家将它推广到更一般的情形。其表述如下：

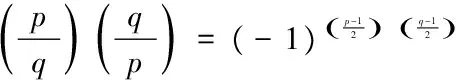
(二)尺规作图

几千年前，古希腊的数学家们曾经深入的研究过一类作图问题，那就是：怎么样运用尺规作内接正多边形。早在《几何原本》一书中，大数学家欧几里德就用尺规完成了内接正三边形、正四边形、正五边形，甚至正十五边形的作图。然而正7、9、11…边形却未能做出。这让欧几里德之后的许多数学家感到尴尬的是，自从欧几里德完成一部分尺规作图的后2000多年中，有关正多边形的尺规作图，仍然只是停留在欧几里德给出的一些内接正多边形的作图方法，其他的并没有任何的进步。直到1796年，年仅19岁的高斯发现了正十七边形的尺规作图方法。这在当时的数学界来说，可是引起了相当大的震撼。

在经过反反复复研究后，高斯在1801年终于对尺规作图问题给出了一个完美的回答。高斯指出，如果仅仅用圆规和直尺，作圆内接正a边形，当a满足如下的形式之一时就能运用尺规作图完成：

(1)a=2k,k=2,3,…

阿里终于见到他朝思夜想的母亲。他情不自禁地仰头发出呵呵的大笑，然后拔腿向母亲身边跑去。他扒开那些花，对着母亲叫道：“姆妈!呵呵。姆妈!呵呵。你回了。”

费马质数是形如：Fk=22k的质数。比如：F0=3,F1=5,F2=17,F3=257…的质数。高斯用代数的方法解决了2000多年一直困扰着人们的几何难题，高斯自然将此视为他平生的得意之作。

通过高斯的证明，正多边形作图的问题与费马数密切的联系在了一起。这就是数学的一大魅力所在，看似两个全无关系的领域竟然用出乎意料的方式，彼此联系到一起。通过“数学王子”高斯的杰出发现，我们可以从中充分的领悟到这种魅力。正是两者的联系，使人们对费马数有了更大的兴趣。

(三)高斯函数

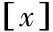
1.高斯函数的几个重要性质：

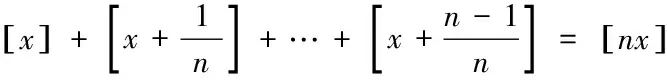
2.高斯函数的求解

高斯函数的求解方法没有固定的模式，根据实际的求解情况，合理的采用适应的求解方法。我们用以下的三种方法来探讨。

严格函数定义求解

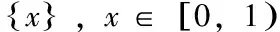
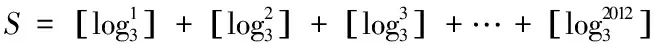
借助对偶式求解

利用对偶式求解高斯函数就是要观察题设中表达式的特点，根据实际情况合理地组建或者构建与之相匹配的相应的表达式，然后通过借助两个表达式之间的高斯函数值的紧密联系，从而间接地求解高斯函数值的方法。

[1]徐品方，数学家传奇丛书[M]，山东教育出版社

[2]周明儒，走近高斯——数学文化小丛书[M]，高等教育出版社

万忠义(1991-)，男，湖北兴山人，成都理工大学，硕士研究生，主要从事优化与控制研究；周小义(1993-)，女，四川安岳人，四川省安岳县乾龙九义校，中学教师。