基于AHP与图论的小区开放对交通影响研究

梁瑞成

(安徽财经大学管理科学与工程学院 安徽 蚌埠 233030)



基于AHP与图论的小区开放对交通影响研究

梁瑞成

(安徽财经大学管理科学与工程学院 安徽 蚌埠 233030)

针对国内小区封闭式设计存在公共资源浪费、交通效率较低等问题，选取路网结构、交叉口、道路设施三类指标，利用AHP分析影响小区周围道路交通的影响因素，结合不同小区地理位置、结构特征选取大连市“兰花小区”与“湖畔小区”作为研究对象，运用图论的思想结合道路阻抗函数量化分析不同小区开放前后的道路通行情况，利用MATLAB进行求解，得出不同小区开放适宜度，因地制宜地提出城市规划中推行街区制的合理建议。

街区制；AHP；图论；道路阻抗；MATLAB

引言

封闭式住区由来已久，存在公共资源浪费、城市公共交通效率低下等问题，中共中央《关于进一步加强城市规划建设管理工作的若干意见》表示新建住宅要推广街区制，原则上不再建设封闭住宅小区，已建成的住宅小区和单位大院要逐步打开，实现内部道路公共化，解决交通路网布局问题，促进土地节约利用。街区制的推广必然使得路网密度提高，道路面积增加。[1]不同小区的面积、位置、外部及内部道路状况等诸多因素不尽相同，随着小区周边主路上进出小区的交叉路口的车辆也会增多，主路的通行速度也会受到影响。因此对于街区制的推广不能一概而论，对于小区道路周边道路通行影响因素以及具体小区开放前后道路的通行水平的研究尤为重要。

一、数据的获取与假设

本文以大连市兰花小区与湖畔小区作为研究对象，所获取的数据来源于统计年鉴以及当地交通部门统计资料。为便于研究做出以下假设：(1)数据真实可靠；(2)司机对小区周围路况十分熟悉，能够选择最短时间到达目的地的路径；(3)不考虑小区开放前后行人、路侧停车等对交通延误时间的影响；(4)不考虑极端天气、交通事故等对道路的影响；(5)小区开放后的道路都属于道路支路，且每一个交叉口路口都设置了无控制信号灯。

二、基于AHP的小区周边道路通行影响因素分析

为分析小区周边道路通行影响因素，结合实际情况与相关研究建立指标体系，如图1所示。

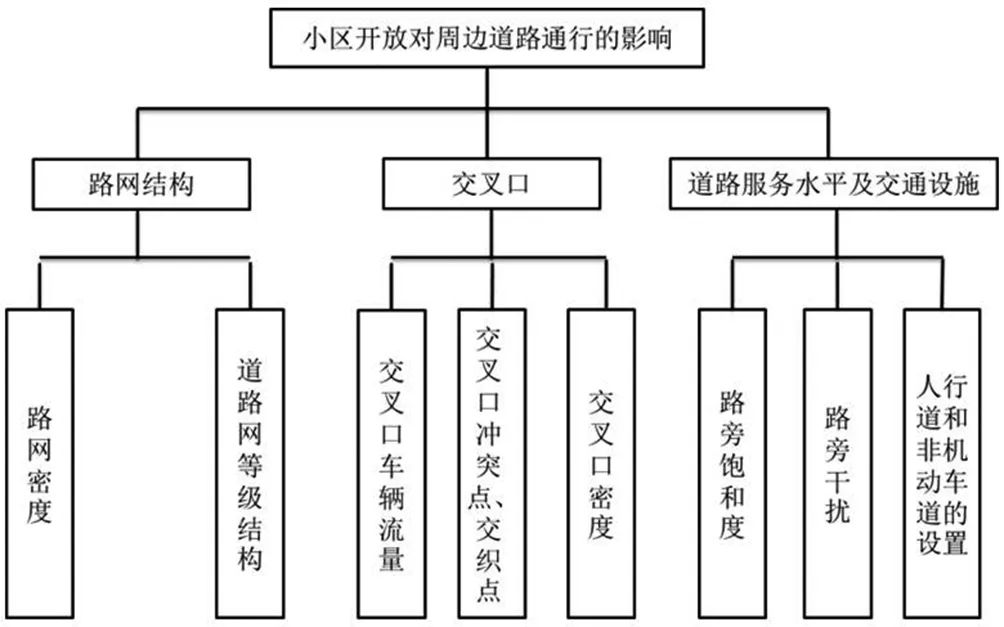
图1 小区周边道路通行评价指标体系

(一)指标的筛选

对于小区开放对道路通行的影响的三个层次：目标层(A)、准则层(B)和方案层(C)，分别对应图2中体系的三个层次准则层从左至右分别表示为B1、B2、B3,方案层分别为C1、C2、…、C8。根据专家判断各指标间相对总要性，构造判别矩阵，得到判别矩阵。

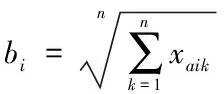
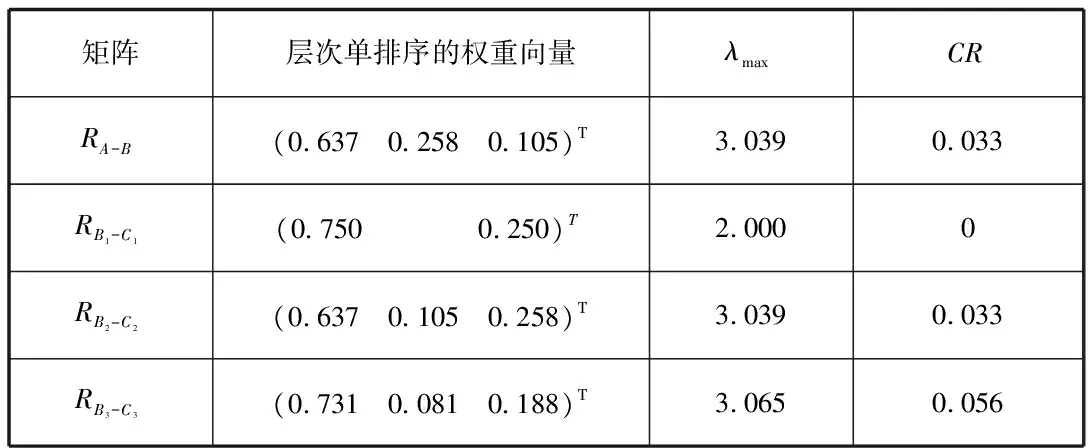
表1 层次单排序权重及一致性指标相关数据

四个层次单排序的CR值均小于0.1，均符合一致性要求，对其进行层次总排序的一致性检验，得出CR=00.0527<0.1，故层次总排序也通过一致性检验。计算结果表明，C4、C7、C8为弱权重指标，将其筛除，所剩余的影响因素为路网密度、道路等网等级结构、交叉口车流量、交叉口密度、路段饱和度。

(二)指标结果分析

根据AHP结果，对于小区开放前后的周边道路通行影响因素中，路网结构与交叉口占据较大比重，道路服务水平与交通设施影响相对较小。因此，街区制下，小区开放前后增加了城市道路路网结构，形成了新的路网结构同时增加了道路交叉口的数量对道路通行的影响最大。考虑到不同小区的面积、位置、外部及内部道路状况等诸多因素不尽相同，为达到因地制宜的推广街区制，本文将大连市本文以大连市兰花小区与湖畔小区进行对比，需要进行进一步的研究。

三、基于图论的小区开放适宜度研究

(一)研究思路

大连市兰花小区与湖畔小区在面积与道路结构等方面存在着明显的差异，根据实际数据，兰花小区的面积约为120000m2，湖畔小区的面积约为20800m2。

图2 小区平面图

小区开放前后周边道路通行受到影响的直观表现是在道路上从起始地到目的地所需要的通行时间改变。根据相关研究，结合道路阻抗BRP函数可以直接计算车辆在某段道路行驶的时间。根据我国道路具体通行的情况，可以通过调查得到城市道路的影响的指标数据以及道路的通行时间，建立如下的道路阻抗BRP函数模型[8]：

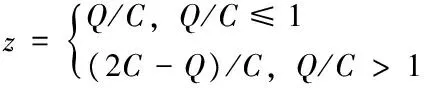
鉴于小区开放还未在全国实行，道路阻抗BRP模型更多的适用于小区开放前道路通行时间的计算。小区开放以后会导致小区道路与主干道、次干道等形成的交叉路口，交叉路口所延误的时间计算直接影响着城市道路交通的规划。因此需要考虑交叉口延误，对BRP函数进行修正。在假定条件下，小区开放后小区道路与其他路的交叉口以及小区内部道路只建立无控制信号指示灯，只考虑在无控制信号灯条件下的交叉口延误。综合考虑修正后BRP模型和新增交叉口后，进一步修正得到车流量在小区周围的道路上行驶所需的时间为：t=t(0)+nd=t0[1+α(Z)β]+nd(n为车流量通过的道路中新增的路口数，d为每一个交叉口所延误的时间)。为方便研究，结合大连市当地具体情况，我们d=6.5s。在此基础上，根据兰花小区与湖畔小区具体路网结构数据，绘制小区开放前后的路网图。

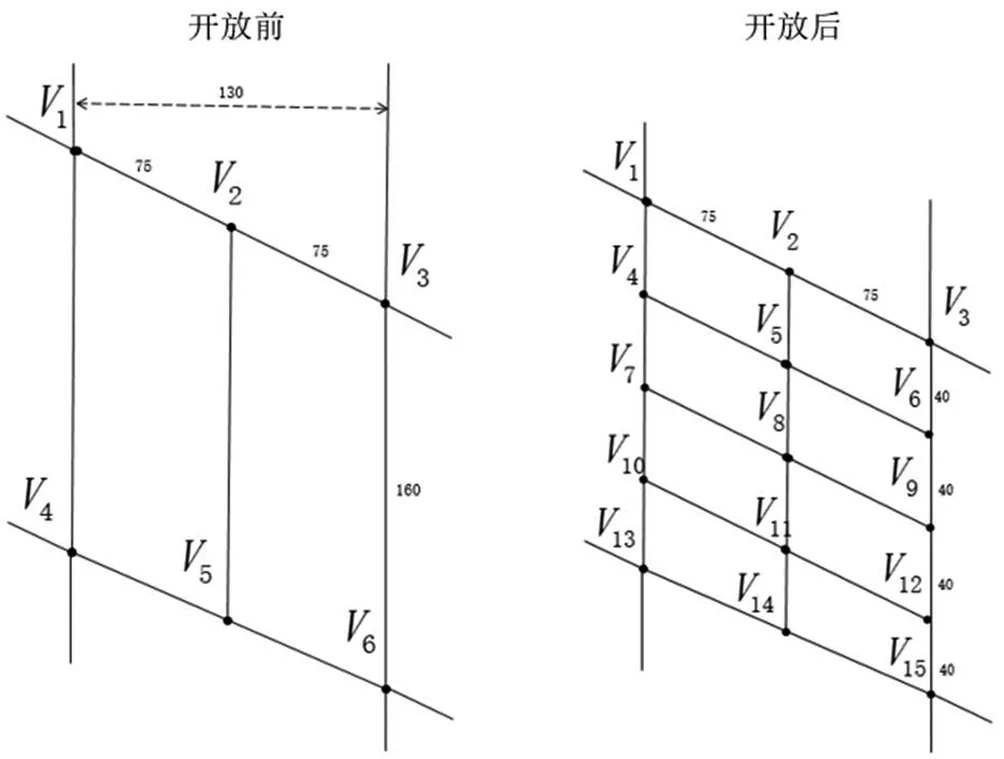
图3 小区开放前后示意图

结合图论，将每个道路交叉口用Vi(i=1,2,3,…,n)表示，可以根据相邻点Vi,j之间的距离，通过修正后的道路阻抗函数得到任意两点之间的通行时间ti,j。根据相邻两点之间的时间ti,j建立道路通行时间方阵：

A=(ti,j)n×n(i=1,2,…,n；j=1,2,…,n)，其中ti,j表示从Vi不经过其他点直接到Vi的通行时间。当无法直接到达时，或者道路不通时，令ti,j为无穷大。利用Dijkstra算法可以计算从Vi到Vi的最短通行时间Ti,j。从而计算小区开放前后从Vi到Vj的最短时间Ti,j。T1,n则为车辆从小区一角到另一角的最短时间，当T1,n越小的时候，车辆通过小区的时间越短，小区周边道路通行情况越好。通过改变道路饱和度Z，计算小区开放前后以及两个小区之间的T1,n的大小，定量分析不同状况下的小区开放前后道路通行是改变情况。

(二)结果与分析

根据相关模型结合大连市的交通数据，得到修正后的阻抗BRP函数如下：

将饱和度z值从0至2每隔0.1依次取值，通过饱和度可以反映车流量的大小，可得车辆在任意相邻两点之间通行时间。利用MATLAB编程计算得到结果，绘制两个小区的开放适宜度折线图：

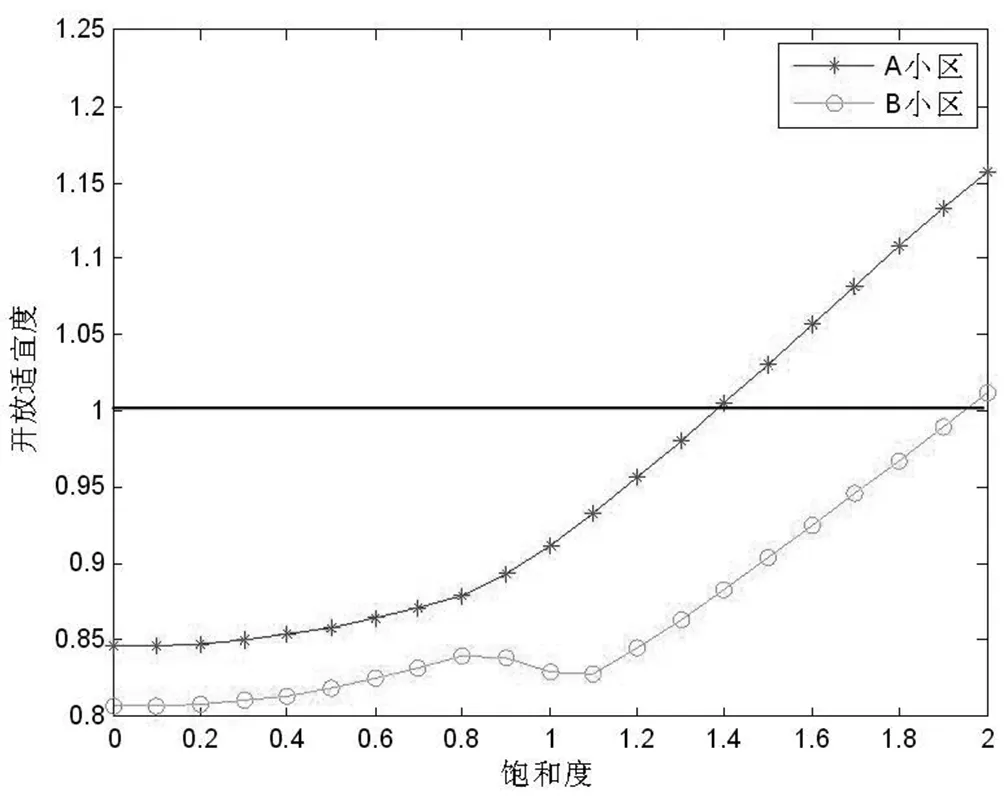
图6 两小区开放适宜度对图

综合表中的数据和绘制的折线图，可以发现，随着交通饱和度z的增加，开放适宜度ε处于上升的状态。即在交通饱和度较低的情况下，即小区周围车流量较低时，ε<1，小区开放并不能改善交通状况，反而因为开放后增加的交叉路口使得道路通行时间增加；在交通饱和度较高的情况下，小区周围车流量较大，ε>1，此时开放小区可以使得道路通行时间缩短，有利于道路交通。

对比两小区的开放适宜度ε，可以发现兰花小区的开放适宜度始终高于湖畔小区，两小区的道路网络类似，但兰花小区的规模面积将近是湖畔小区的6倍。分析可知，面积大的小区相对于面积小的小区开放后，在道路交通的影响方面更有利一些。同时也可以反映随着小区内开放的道路的增加，新增道路所能带来的交通有利程度在减少。

四、总结与建议

根据小区开放对道路通行的影响的研究结果，可我们向城市规划部门提出以下建议：

1.街区制的推广会对小区周边道路的路网密度、交叉口密度等产生影响，在进行小区开放的规划或管理时要注重提升路网密度，尽量减少交叉口数目，以避免原道路通行能力受到较大影响。在新增的交叉路口要注重管理，设置红绿灯或交警以保证交通。

2.小区开放后能否有利于交通通行与小区所处位置周边车流量有关，街区制推行与否需要对周边道路车流量大小进行实地观测，对于周边道路车流量较大的小区，可以进行开放，利用形成的支路对主干道路进行分流，以缓解之前的交通压力；对于周边道路车流量较小的小区，开放后对交通通行压力的缓解并不大，反而可能因为新增道路使得交叉口增加，从而降低了原有道路的通行能力。

3.小区本身规模大小，是小区开放影响交通的重要因素。规模较大的小区相比规模较小的小区开放后对周边道路交通通行的有利影响更大，根据小区周边道路情况对较大规模的小区进行开放，对于规模较小的区，可以考虑不进行开放。

4.小区开放产生的效果，有关部门要考虑其周边道路结构，如果小区开放后能够与周围道路较好的连接成道路网，则会更大程度的有利于交通通行。此外，小区开放后，交通通行进入小区内部，可能会增加安全隐患，城市规划和交通管理部门需要着重考虑，对于新增道路，要尽量降低发生事故的风险。

[1]聚焦《关于进一步加强城市规划建设管理工作的若干意见》[J].中国勘察设计，2016，04:18 -19．

[2]刘宁.城市道路阻抗模型的研究与应用[D].大连：大连理工大学，2012

[3]吴海燕，张蕊.交叉口综合评价指标体系[J].中国市政工程，2001(3)：17-20

[4]郑伶俐.交通影响程度评价指标及方法研究[D].上海：同济大学,2008

[5]陈仲常，杨琳.熵权模糊综合评判法在人口综合发展评价模型中的应用[J].统计与信息论坛，2008,23(12):26-30

[6]高晗.城市道路无信号控制交叉口行车延误的分析[J].辽宁省交通高等专科学校学报，2003,5(4)：1-2

[7]何南,赵胜川.城市道路阻抗函数模型研究——以大连市为例[J].公路交通科技，2014,31(2):104-108

梁瑞成(1996-)，男，汉族，安徽合肥人，安徽财经大学管理科学与工程学院本科在读，研究方向：工程管理。