生物网络关键节点识别方法研究进展

彭秀芬

( 池州学院 数学与计算机学院，池州 247000 )

生物网络关键节点识别方法研究进展

彭秀芬

( 池州学院 数学与计算机学院，池州 247000 )

生物网络是一类典型的复杂网络，其关键节点的识别方法大多来自于其他复杂网络的研究。首先举例分析了复杂网络中常用的几种判断节点关键性的指标，然后总结了几种生物网络关键节点的识别方法，指出了生物网络节点关键性识别与其他复杂网络的区别及今后研究的方向。

图论；复杂网络；中心性指标；生物网络；关键节点

随着系统生物学的发展，生物学研究从单基因、单分子的功能探索发展到研究细胞组成物质及其生命活动对分子功能的影响。细胞组成物质包括蛋白质、DNA、RNA、小分子等。研究这些物质的相互作用，可通过建立网络模型来完成。常见的生物网络有：蛋白质-蛋白质相互作用网络(Protein-protein interaction network, PPI network)、代谢网络(Metabolic network)、基因调控网络(Regulatory network)等[1-5]。这几种网络模型中，节点分别代表蛋白质、代谢物及基因，边代表其作用关系。

在生物网络中，各节点的生物功能不同，对整个网络的影响也不同。也就是说生物网络中节点的地位与其在细胞功能上的重要性有关，某些节点(关键节点)的存在对网络结构和功能具有重大意义[6-7]。例如，在蛋白质相互作用网络中高度关联的节点具有重要的功能，而且其缺失与致命性有关[8]。在基因调控网络中，也需要识别哪种基因控制着许多其他基因，以便其能被当作有机体的全局调节因子进行分析。因此，分析和研究生物网络关键节点及其相互关系，对系统生物学研究越来越重要。然而，经常遇到的问题是不能明确地回答哪些节点是关键性节点。

生物网络的结构特性表明其是典型的复杂网络[9]。为了研究这些大型的复杂网络，研究者们提出了各种不同的网络分析方法，也使用了其他科学领域的分析方法。本文首先分析了几种以图论为基础的判断复杂网络节点关键性的指标——中心性指标，然后总结了几种生物网络关键节点的识别方法，分析了生物网络节点关键性识别与其他复杂网络的区别，并指出了今后研究的方向。

1 节点的关键性指标

目前，在复杂网络关键节点的识别方面，国内外的很多研究都是以图论为基础，量化关键节点与非关键节点在拓扑性质方面的差异，并以量化值的结果大小作为判别节点关键与否的标准[10-11]。相关图论概念参考了文献[12]。

1.1 中心性指标

复杂网络关键节点的识别可通过对节点的关键性进行排名来完成。一般情况下，事物的排名都是建立在某个相关数值的基础上。例如，中超联赛是根据比赛积分进行排名。在识别复杂网络关键节点的过程中也可以使用相同的方法对节点的关键性进行排名。根据所研究的问题，为每个网络节点分配一个表示关键性的数值，然后依据这些数值对节点进行排名。节点所得的数值称为该节点的中心值，而为每个节点分配数值的函数称为节点的中心性指标，其定义如下：

定义1：设G=(V,E)是一个有向图或无向图，函数C：V→R称为一个中心性指标[13]。

中心性指标为每个节点分配的实数值可以进行两两比较，例如，任意两节点x和y，若C(x)>C(y)，则表明节点x比节点y更重要。

1.1.1 度(Degree)中心性指标

网络中任意节点x都有自己的度值d(x)。根据这些度值，可以对网络中的节点进行排名，因而可以形成了一个中心性指标——度中心性指标，记为Cdeg。计算任意节点x的度指标中心值的公式如下[14]：

Cdeg(x)=d(x)

(1)

度指标是一种基于本地的中心性指标，考虑的是相邻节点的情况，反映了节点与周围节点之间建立直接关系的能力。节点的度中心值越高，与之相邻的节点就越多，其在网络中的地位和功能相对来说就可能更重要。任何网络都可使用该中心性指标对节点进行排名。在有向网络中，度指标根据边的方向又分为入度指标和出度指标。

1.1.2 离心率(Eccentricity)中心性指标

在网络模型中，常利用节点间的通信来模拟其所表示的对象之间的相互关系。在研究过程中，通常的做法是假设节点间的通信是通过它们之间的最短路径来完成的。分析网络拓扑结构，可以发现其他任意节点都能以较短的距离到达居于网络拓扑结构中心的点。根据这个思想，Hage和Harary在研究社会网络时，提出了离心率中心性指标[15]。该中心性指标首先要计算节点的离心率。而节点的离心率为当前节点到其他所有节点之间的最短路径长度中的最大值。节点x的离心率记为ecc(x)，其离心率越大，就越偏离网络拓扑结构的中心，其地位也就越低。根据中心性指标的定义，取节点的离心率的倒数作为其中心值，记为Cecc。计算任意节点x的离心率指标中心值的公式如下[16]：

Cecc(x)=1/ecc(x)

(2)

其中，ecc(x)=max{dist(x,y):y∈V}，dist(x,y)为节点x和y之间的最短路径长度。

离心率指标以整个网络结构的中心为基准，考虑了每个节点在网络中的权益。哪个节点离网络中心越近，对其他任意节点来说，该节点传递信息的速度就比较快，其在网络中的地位也就越高。在解决实际问题时，虽然有些问题要考虑每个节点的权益(例如医院选址)，但有些问题则要考虑整体效益(例如商场选址)。

1.1.3 紧密度(Closeness)中心性指标

有研究指出，处于网络节点密集中心的点到其他节点的平均最短路径长度最短，其能够更快地将信息传达到整个网络，在网络通信中起到了关键作用。如何找到这样的关键节点呢？学者们提出了紧密度中心性指标，记为Cclo。

利用紧密度中心性指标为每个节点分配中心值时，先要计算每个节点到其他节点的最短路径长度的总和。这样，居于节点密集区域中心的节点会得到一个较低值(总和越小，平均长度就越小)。根据中心性指标定义，中心值越大的节点其地位越重要，所以将最短路径长度总和的倒数作为节点的中心值。计算任意节点x的紧密度指标中心值公式如下[18]：

Cclo(x)=1/∑y∈Vdist(x,y)

(3)

其中，dist(x,y)为节点x和y之间的最短路径长度。

紧密度中心性指标反映的是当前节点与其他节点之间连接的密切程度，其最早被用于社会网络中心性的研究。Wuchty等用紧密度中心性指标探讨了复杂网络中心性问题，阐明了地方设施选址问题[18]。在生物网络研究领域，这种中心性指标应用也很广泛。

1.1.4 最短路径介数(Shortest path betweenness)中心性指标

在网络通信中，有些节点扮演了通信“枢纽”的角色，这些节点被删除或破坏，部分节点间的通信会被中断，甚至整个网络会陷入瘫痪。因此，从通信量的角度考虑，节点的通信量越大，其在网络中的地位就越重要。因此，可以利用网络中所有最短路径中经过某个节点的路径的数目占最短路径总数的比例，来衡量该节点在网络中的地位[19]。

网络中任意两节点间的最短路径上的其他节点都承担了这两点间的通信流量。服务对象越多的节点(即经过该节点的其他节点间的最短路径越多的节点)，其对于整个网络的通信来说就越重要。计算经过一个节点的通信流量，并将这个数值作为度量其是否是关键节点的指标，就得出了一个中心性指标定义——基于最短路径的介数中心性指标，记为Cspb。

设节点y是节点x和z之间最短路径上的内部节点(y≠x且y≠z)，计算节点y的基于最短路径介数指标中心值公式如下[21]：

(4)

其中δxz(y)表示节点y所承担的节点x到z的通信比率，其值为σxz(y)/σxz。而σxz表示两节点x和z之间的最短路径数目，σxz(y)表示两节点x和z之间的经过节点y的最短路径数目。如果x和z之间没有最短路径存在(σxz=0)，则δxz(y)=0。

利用介数指标可以确定信息负载繁重的网络节点。节点介数中心值越大，其对网络通信功能的影响就越大。

1.1.5 特征向量(Eigenvector)中心性指标

之前介绍的中心性指标描述的是一个节点对其他节点的影响，但在有些情况下，节点在网络中的地位和功能与其邻居的中心性有很大关联。若一个节点拥有高中心值的邻居，该节点也会有比较高的中心值[20]。这种中心性思想是菲利普·玻纳西奇提出的，他不仅考虑了节点在网络中的位置，而且考虑了相邻节点的反馈信息。这种思想被形式化为一组线性方程，该方程组的最大特征值λ所对应的特征向量就是各个节点的中心值，记为Ceiv。对于任意节点vi，其特征向量中心值计算公式如下[21]：

(5)

其中，aij表示所分析的网络的邻接矩阵A的相应元素。如果节点vi和vj之间没有边存在，则这个元素之为0，其与Ceiv(vj)相乘后，相应的项消除。

特征向量指标从节点的地位和影响力角度考虑，把单个节点的影响力归结为所有其他节点影响力的线性组合，不仅能够体现节点在网络结构中的地位，更能反映节点的长期影响力。

1.2 几种中心性指标比较分析

为了更好地了解以上介绍的几种中心性指标及其优缺点，下面使用了一个网络示例图(如图1所示)，用以展示不同中心性指标对应的各个节点的中心值(如表1所示)。

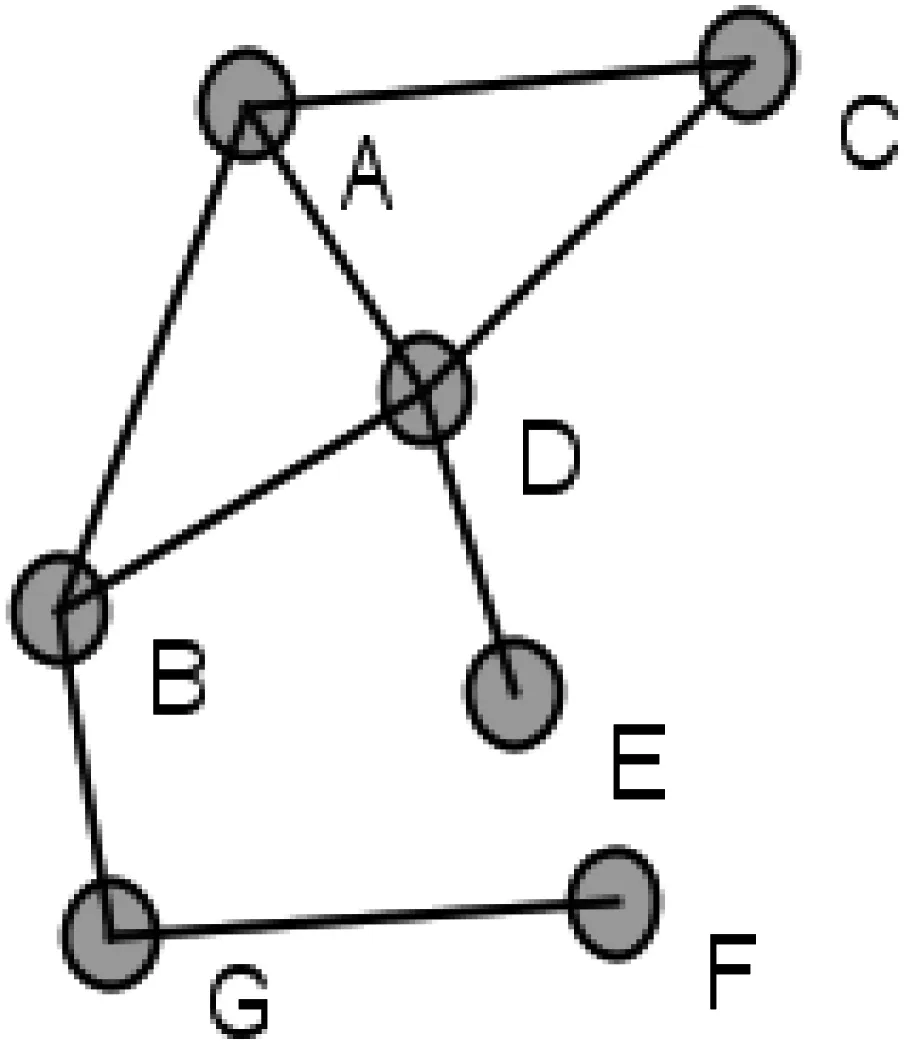
图1 网络示例图

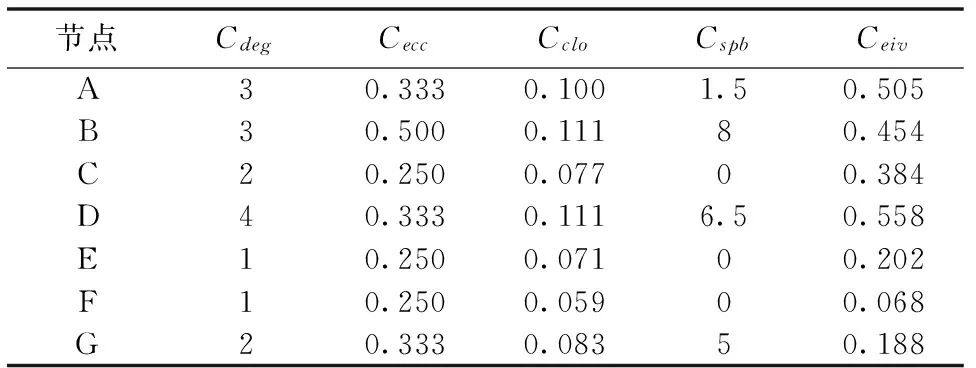
节点CdegCeccCcloCspbCeivA30.3330.1001.50.505B30.5000.11180.454C20.2500.07700.384D40.3330.1116.50.558E10.2500.07100.202F10.2500.05900.068G20.3330.08350.188

在这些中心性指标中，度指标直接使用了网络中节点的度信息，反映了一个节点与其邻居节点建立直接联系的能力，未考虑节点对整个网络结构的影响力。实际研究中也表明，仅仅从度值的角度判断关键节点不是很准确。例如图1中，节点A的度中心值比节点G的大，说明节点A比G更重要，但删除节点A后(如图2所示)，网络仍然是连通的，而删除节点G后(如图3所示)，网络被分解成两个互不连通的部分。从这个网络连通角度考虑，显然节点G比节点A重要，是维护网络连通性的关键节点之一。

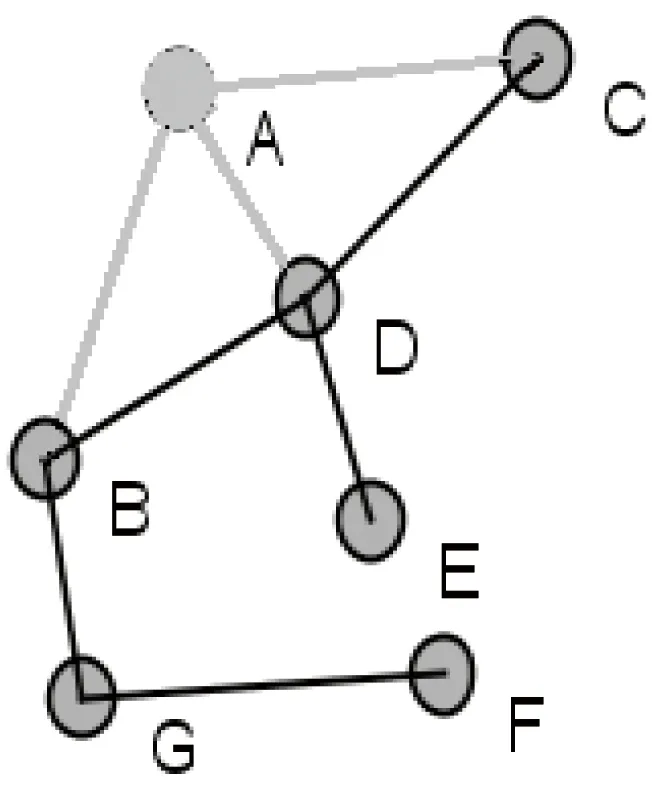
图2 删除节点A的示例图

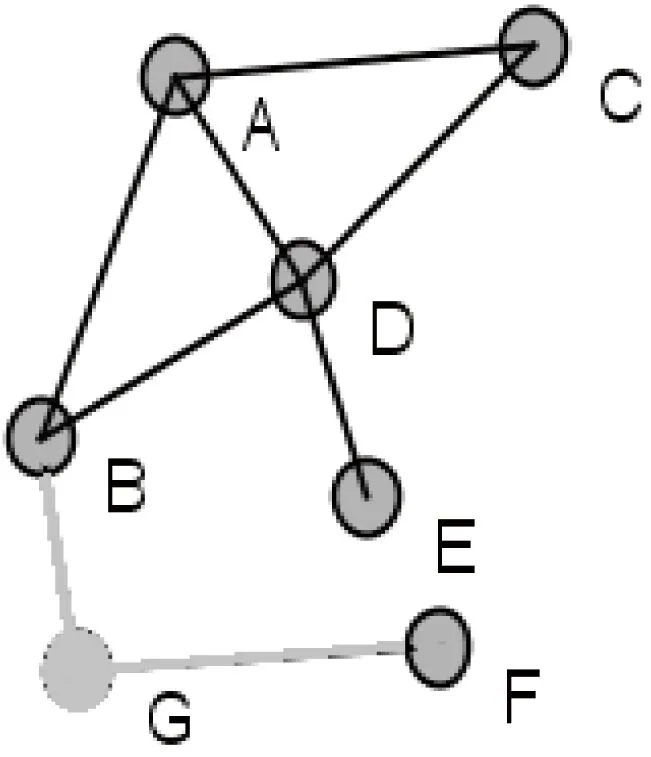
图3 删除节点G的示例图

离心率、紧密度和最短路径介数等中心性指标都利用了网络图的最短路径信息，区别在于离心率和紧密度中心性指标使用的是两点间的最短路径长度，其中，离心率指标考虑的是单一通信距离，反映了当前节点与网络拓扑结构中心的远近关系。由表1可知，图1网络中的节点B的度虽然比节点D的小，但它更接近于网络拓扑结构的中心。紧密度指标关注的是节点与所有其他节点的平均通信距离，其反映了当前节点与网络节点密集区域中心的距离关系。例如，图1网络中节点B的紧密度中心值与节点D的相同，说明这两个节点与密集中心的距离相同，即在这种指标下，节点B和D具有同等的关键性。最短路径介数指标使用的是经过节点的最短路径数目，计算节点所承担的通信量。这种指标关注的是节点对整个网络连通性的影响。图1中，节点A和B的度都是3，但节点B能影响到整个网络的连通性，且比节点D的影响更大。

特征向量指标是利用邻居节点的反馈信息，衡量一个节点在网络结构中的地位及其影响力。对于任意节点，其邻居节点的特征向量中心值越高或者邻居越多，该节点的中心值也就越高。图1网络中的节点E和F，都是度为1的节点，即网络边缘节点。由于E的邻居D比F的邻居G的中心值要高，因此E得到一个相对高一点的特征向量中心值。

通过以上分析可见，不同的中心性指标是根据所研究的特定问题而定义的。对于同一个网络，应用不同的中心性指标对网络节点进行排序时，得到的结果会有很大差异。因此，即使是同一个网络，不同中心性指标的中心值之间没有可比较性。另外，对于不同的网络，同一种中心性指标的中心值也没有可比性。在研究不同的生物网络关键节点时，也应根据具体的问题选择合适的中心性指标，可以结合多种中心性指标，从不同的角度分析其节点的关键性。

2 生物网络关键节点的识别方法

在生物网络关键节点识别研究中，研究者利用网络模型模拟生物体细胞内的物质活动。这些网络模型大多数情况下表现出了小世界特性和无标度特性，因此，研究者们直接使用或扩展了其他复杂网络的研究方法，用以识别其关键节点。

2.1 生物网络模型

不同的生物网络，其物质之间的作用关系有所不同，因此，在分析研究各种生物网络时所使用的具体的网络模型也有所区别。例如，在研究细胞中蛋白质的作用时，各种蛋白质被看作一个节点。由于蛋白质与蛋白质之间会相互影响，代表蛋白质的节点与节点之间就具有相互影响的关系，这种关系被看作一条无向边，因此形成了用无向图所表示的蛋白质-蛋白质相互作用网络(图4)；代谢网络中，节点之间具有先后的转换关系，其通常使用的是有向图(图5)；基因调控网络的各节点之间具有调控和被调控的关系，所以也使用有向图进行分析。

图4 酵母蛋白质-蛋白质相互作用网络模型[22]

图5 Buchnera aphidicola代谢网络模型[23]

在使用中心性方法分析识别生物网络关键节点时，有的中心性指标要求网络模型必须是(强)连通图。但通常所获取的生物网络模型并非是连通的，会存在一些独立的点或者有一些互不连接的连通子图。一种方法是将不连接的两个点之间的最短路径长度定义为无穷大。另一种方法是根据连通性将网络分解为几个连通分支，再将每个分支作为一个独立的网络进行分析。

2.2 中心性分析法

中心性分析法是根据某种中心性指标计算各个网络节点的中心值，并根据该值对节点进行排序，然后根据节点的排名判断节点在网络中的地位和功能，确定其是否是关键节点。这种网络元素排序方法在识别生物过程中的关键参与者特别有用，可以帮助了解潜在的生物过程。

Jeong等利用度中心性分析了酵母菌的蛋白质-蛋白质相互作用网络，讨论了高中心性值的蛋白质淘汰后对生物体的影响，并证明了高度值的蛋白质成为生物体必需品的可能性要比低度值的蛋白质大[24]。Bergmann等在研究酿酒酵母、大肠杆菌和秀丽隐杆线虫的基因共表达网络(Gene co-expression network)过程中也使用了度中心性指标，发现对有机体来说度高的基因可能更重要[25]。Ma和Zeng[26]根据稍微修改的紧密度中心性方法，识别出了大肠杆菌代谢网络中排第八和第十的代谢物是糖酵解和柠檬酸酸循环通路的一部分。

Joy[27]等在识别酵母关键蛋白质时，发现介数中心值高的蛋白质的度中心值有高有低。特别是具有高介数值和低度值的蛋白质，他们可能维护着网络结构的完整性。Potapov等[28]将介数中心化方法用于研究哺乳动物转录调控网络，并指出在不同元素的生物学意义方面介数是最具有代表性的拓扑特征。

有时为了更准确地分析和识别生物网络中的关键节点，研究人员会同时使用多种中心性指标。Hahn等[29]选取了酵母、蠕虫和苍蝇的蛋白质-蛋白质相互作用网络，并利用度、紧密度和介数指标分析比较了这3个网络中的关键节点，结果显示关键节点的平均中心值明显高于非关键节点的中心值。Estrada[30]利用应用度、紧密度、介数、特征向量等多种中心性指标，分析了酵母的蛋白质-蛋白质相互作用网络，其研究表明中心性指标能够比随机选择策略更好地识别关键蛋白质。

2.3 其他识别法分析

由于中心性指标是根据特定的问题定义一个函数，为网络中的每个节点分配一个中心值，因此单一的中心性指标所提供的生物信息比较有限。生物网络中各个节点的功能及其相互关系比较复杂，单独使用这些指标参数所获得的关键节点的生物学意义比较低，且存在一些缺陷。为此，一些研究者提出了使用综合参数识别生物网络关键节点的方法，也有一些人另辟蹊径。

黄海滨等[31]在相关研究中，将关键蛋白质识别看成是一类特殊的模式识别，以分子之间的量化关系(拓扑参数)为依据，利用复合参数来识别蛋白质网络中的关键节点。对于蛋白质网络中的任意节点vi，他们将各种中心性指标得到的中心值，作为该节点的拓扑参数集，并将所有节点的拓扑参数集组成一个矩阵——关键节点识别矩阵，其元素就是节点在对应的中心性指标下的中心值。在分析了各参数与节点关键性的相关性和参数之间的相关性后，选择合适的参数组成复合参数。根据复合参数中的一个参数对关键节点识别矩阵进行排序，筛选出若干节点，然后再根据其他参数进行识别。其实践表明这种复合参数异步识别法的性能明显高于独立参数识别法。

杨汀依[32]在以往识别方法的基础上，提出了灰色关联分析法和熵权法来建立各种中心性指标之间的关系，综合考虑多个中心性指标，从而确立网络的关键节点。灰色关联分析法是依据各因素间发展趋势的相异或者相似程度，期望通过特殊的方法，寻找它们之间的数值关系，这种关系指的是中心性指标关联系数和节点的关联度。节点的关联度越大，说明其越重要。在信息论中，熵表示的是不确定性的量度，其值越小，信息的效用值就越大，反之，信息的效用值就越小。将节点和指标值矩阵作为信息的载体——判断矩阵，并以此计算出各个中心性指标的熵权值[32]。在利用灰色关联分析法分析计算每个节点的关联度时，引入熵权值，提高了节点关联度的准确性。

Ulitsky和Shamir[33]扩展了Kelley和Ideker的将遗传网络和物理网络一起分析的方法，将蛋白质-蛋白质相互作用网络和对应的遗传网络结合起来，开发了独特的分析工具，在物理环境下分析遗传交互。在该研究中，蛋白质-蛋白质相互作用网络中的一个连通子图被定义为路径(pathway)，通过贪婪算法获得遗传网络中相互之间有密集交互的两个不同路径，这种关系定义为关联路径模式(Between-pathway-model,BPM)。他们通过该方法获得了140种模式，同时确定了与所在模式中的两条路径都有许多物理交互的“枢纽”蛋白质，并发现了其中的关键蛋白质。

陆聿[34]将基础物理学中的“势场”概念运用到蛋白质-蛋白质相互作用网络的拓扑结构中，提出了一种基于拓扑势的蛋白质-蛋白质相互作用网络关键节点识别方法。该方法的基本思想是将网络中的每一个节点都当作一个物理粒子，在它周围存在一个虚拟的作用场，由此网络中所有节点的相互作用就联合形成了一个势场；采用高斯势函数来描述网络中节点间的相互作用，其对应的场就是拓扑势场；通过对每一个节点的拓扑势的值进行定义和计算，就能够获得一个基于网络拓扑势的反映节点关键性的精确排序。

丁德武和彭秀芬[35]提出了从节点对社团贡献的角度来识别关键节点的方法。该方法首先采用复杂网络链接聚类算法从生物网络中提取富含生物学功能意义的社团。这些社团是相互交叠的，网络中某些节点可能属于多个社团，因此可以根据这一点来评价节点的关键性。研究人员分别从激酶与磷酸酶交互网络和小RNA调控网络提取了10个和14个富含生物学功能意义的社团，并识别了其中连接最多社团数量的节点。这种方法不仅分析了生物网络拓扑结构，还研究了节点对生物网络功能关系的影响，依据节点对生物网络功能的贡献值，识别出了具有生物学意义的关键节点。

丁德武[36]还提出了利用主成分分析法来研究代谢网络的中心化问题。该方法是选取节点的P个指标(x1,x2,…,xp)，并对其进行标准化。然后，根据标准化后的数据矩阵建立相关系数矩阵R，求出R的特征值及其对应的特征向量，并由累积方差贡献率确定主成分的个数及各个主成分。最后，选取累积贡献率最高的主成分，并根据对应的线性方程分析主成分的值，以确定各个节点的排名。

上述关键节点识别方法都是通过特定的方法为节点赋值，并根据该值对节点进行排序，并据此确定关键节点。研究表明生物网络节点的关键性不仅仅由网络拓扑结构决定，还受到节点自身生物学功能意义和细胞物质遗传特性的影响[37-39]。

3 结语

生命科学的发展带动了生物网络相关研究的进步，分析研究生物网络的关键节点及其相互关系，可以从生物信息学角度为医药发展提供有价值的理论和方法。本文从复杂网络理论和图论出发，讨论和分析了几种用于节点关键性排序的指标和识别关键节点的方法。这些生物网络关键节点的识别方法各有所长，共同点都是以网络拓扑结构为基础，分析研究节点间的相互关系以确定节点的关键性。生物网络与其他复杂网络的区别在于其节点具有生物学意义，在今后的研究中应更多地考虑细胞物质的生物学信息，才能更准确地识别具有实际生物学意义的关键节点。

[1]RUAL J F, VENKATESAN K, HAO T, et al. Towards a proteome-scale map of the human protein-protein interaction network [J]. Nature, 2005, 437(7062):1173-1178.

[2]STELZL U, WORM U, LALOWSKI M, et al. A human protein-protein interaction network: a resource for annotating the proteome [J]. Cell, 2005, 122(6):957-968.

[3]JEONG H, TOMBOR B, ALBERT R, et al. The large-scale organization of metabolic networks[J]. Nature, 2000, 407 (6804):651-654.

[4]DUARTE N C, BECKER S A, JAMSHIDI N, et al. Global reconstruction of the human metabolic network based on genomic and bibliomic data[J]. Proc Natl Acad Sci USA, 2007, 104 (6): 1777-1782.

[5]CARNINCI P, KASUKAWA T, KATAYAMA S, et al. The transcriptional landscape of the mammalian genome[J]. Science, 2005, 309 (5740): 1559-1563.

[6]GIRVAN M, NEWMAN M E J. Community structure in social and biological networks [J]. Proc Natl Acad Sci USA, 2002, 99(12): 7821-7826.

[7]CRUCITTI P, LATORA V, MARCHIORI M, et al. Error and attack tolerance of complex networks[J]. Nature, 2000, 406(6803): 378-382.

[9]YAMADA T, BORK P. Evolution of biomolecular networks-lessons from metabolic and protein interactions [J]. Nature Reviews Molecular Cell Biology, 2009, 10(11): 791-803.

[10]丁德武,陆克中,须文波, 等. 基于SAA的苏云金杆菌代谢网络功能模块[J]. 计算机工程, 2010, 36(13): 162-163.

[11]DING D W, HE X R, PENG X F, et al. Functional modules and central proteins in ROS network[J]. Computers and Applied Chemistry, 2012, 29(6): 749-752.

[12]徐俊明.图论及其应用[M]. 合肥:中国科学技术大学出版社,2004:1-5.

[13]JUNKER B H, SCHREIBER F. Analysis of biological networks [M]. Hoboken:Wiley, 2008:65-67.

[14]JUNKER B H, SCHREIBER F. Analysis of biological networks [M]. Hoboken:Wiley, 2008:69.

[15]HAGE P, HARARY F. Eccentricity and centrality in networks [J]. Social Networks, 1995, 17(1):57-63.

[16]JUNKER B H, SCHREIBER F. Analysis of Biological Networks [M]. Hoboken:Wiley, 2008:72-74.

[17]KOSCH TZKI D, SCHREIBER F. Comparison of centralities for biological networks[J]. Proc German Conf Bioinformatics(GCB 2004), 2004, 53(1):199-206.

[18]WUCHTY S, STADLER P F. Centers of complex networks [J]. Journal of Theoretical Biology, 2003, 223 (1):45-53.

[19]BARTH LEMY M. Betweenness centrality in large complex networks[J]. The European Physical Journal B, 2004, 38(2):163-168.

[20]BONACICH P, LLOYD P. Eigenvector-Like measures of centrality for asymmetric relations[J]. Social Net-works, 2001, 23(4):191-201.

[21]JUNKER B H, SCHREIBER F. Analysis of Biological Networks [M]. Hoboken:Wiley, 2008: 79.

[23]BORENSTEIN E, KUPIEC M, FELDMAN M W, et al. Large-scale reconstruction and phylogenetic analysis of metabolic environments[J]. Proc Natl Acad Sci USA, 2008, 105(38): 14482-14487.

[24]JEONG H, MASON S P, BARABASI A L, et al. Oltvai ZN: Lethality and centrality in protein networks[J]. Nature, 2001, 411(6808):41-42.

[25]BERGMANN S, IHMELS J,BARKAI N. Similarities and differences in genome-wide expression data of six organisms[J]. PLOS Biology, 2004, 2(1):E9.

[26]MA H W, ZENG A P. The connectivity structure, giant strong component and centrality of metabolic networks[J]. Bioinformatics, 2003, 19(11):1423-1430.

[27]JOY M P, BROCK A, INGBER D E, et al. High-betweenness proteins in the yeast protein interaction network[J].Journal of Biomedicine and Biotechnology, 2005(2):96-103.

[28]POTAPOV A P, VOSS N, SASSE N, et al. Topology of mammalian transcription networks[J].Genome Informatics, 2005, 16(2):270-278.

[29]HAHN M W, KERN A D. Comparative genomics of centrality and essentiality in three eukaryotic protein-interaction networks[J]. Molecular Biology and Evolution, 2005, 22(4):803-806.

[30]ESTRADA E. Virtual identification of essential proteins within the protein interaction network of yeast [J]. Proteomics, 2006, 6(1):35-40.

[31]黄海滨,杨路明,王建新,等. 基于复合参数的蛋白质网络关键节点识别技术[J]. 自动化学报, 2008, 34(11): 1388-1395.

[32]杨汀依. 复杂网络关键节点识别技术研究[D]. 南京：南京理工大学,2011.

[33]ULITSKY I, SHAMIR R. Pathway redundancy and protein essentiality revealed in theSaccharomycescerevisiaeinteraction networks[J]. Molecular Systems Biology, 2007, 3(1):104-110.

[34]陆 聿. 基于拓扑势的关键蛋白质识别方法研究[D]. 长沙:中南大学, 2014.

[35]丁德武, 彭秀芬. 基于交叠社团相似性的生物网络关键节点识别[J]. 计算机与应用化学, 2014,31 (10):1213-1216.

[36]丁德武.基于主成分分析的代谢网络中心化[J]. 计算机与应用化学,2015,32(3):376-378.

[37]马 玲.基于拓扑结构和复合物信息的关键蛋白质识别算法研究[D].长沙:湖南大学.2013.

[38]丁德武.基于链接聚类的代谢网络社团结构研究[J]. 计算机工程与应用,2011,47(34):141-144.

[39]陈传庚, 段 斌, 廖高明，等. 基于基因表达谱和生物网络识别肺癌敏感基因[J]. 国际遗传学杂志, 2015, 38(1):24-28.

Methods for the identification of key nodes in bionetworks

PENG Xiu-fen

(College of Mathematics and Computer Science, Chizhou University, Chizhou 247000, China)

Biological network is a kind of typical complex network, thus the methods for identifying of the key nodes in biological networks are mainly from general complex network methods. This paper introduces several methods for the key indicators in the general complex networks, and then sums up the methods for the identification of key nodes in biological networks. It points out the differences between the biological network key nodes recognition and other general complex networks. The research directions is also discussed.

graph theory; complex network; centrality index; biological network; key node

2016-08-15；

2016-08-19

安徽省高校省级优秀青年人才基金重点项目(生物网络的随机Petri网模型构建与分析，2013SQRL096ZD)；池州学院自然科学研究项目(2013ZRZ003)；安徽省教育厅自然科学重点项目(KJ2015A264)

彭秀芬, 讲师, 硕士, 主要研究领域为生物信息学、计算机应用，E-mail：xiufenpeng@qq.com

Q811.4

A

2095-1736(2017)04-0104-06

doi∶10.3969/j.issn.2095-1736.2017.04.104