面向多敏感属性的匿名隐私保护方法

张荣庆，徐光侠

(1.西南大学 计算机与信息科学学院，重庆 400715；2.重庆市巴蜀中学，重庆 400013；3.重庆邮电大学 软件学院，重庆400065；4.重庆大学 信息与通信工程博士后流动站，重庆 400044)

面向多敏感属性的匿名隐私保护方法

张荣庆1，2，徐光侠3,4

(1.西南大学 计算机与信息科学学院，重庆 400715；2.重庆市巴蜀中学，重庆 400013；3.重庆邮电大学 软件学院，重庆400065；4.重庆大学 信息与通信工程博士后流动站，重庆 400044)

在数据发布过程中，如果对发布的敏感属性信息不进行任何保护处理而直接发布，容易遭受攻击导致隐私信息泄露。针对传统的单敏感属性隐私保护方法在多敏感属性中不能得到很好的隐私保护效果，提出了一种基于多敏感属性相关性划分的(m,l)-匿名隐私保护模型。利用信息增益法对多敏感属性的相关性进行计算并划分，降低敏感属性维度；根据(m,l)-diversity原则对敏感属性分组，保证发布的数据能防止偏斜性攻击，并且在一定程度上降低背景知识攻击的风险；采用聚类技术实现该模型，减小该模型产生的附加信息损失和隐匿率，确保发布的数据具有较高的可用性。实验结果表明，基于多敏感属性相关性划分的(p,l)-匿名隐私保护模型具有较小的附加信息损失和隐匿率，保证了发布数据的可用性。

多敏感属性；匿名；聚类；信息增益

0 引 言

数据挖掘作为一种分析海量信息的强大工具，正运用于社会的方方面面。利用数据挖掘技术可以得到有规律和有价值的信息，但又会带来隐私信息泄露的危害。原因在于可以通过数据挖掘分析出这些信息中包含的隐私信息，这些隐私信息通常都是政府、企业或个人不愿意让外界知晓的。因此，在有效地挖掘分析海量信息得到有规律和有价值信息的过程中，如何对其中的隐私信息进行安全保护是一项重大的挑战。

目前，数据发布中的隐私保护(privacy preserving in data publishing，PPDP)研究主要从法律和技术2个角度开展。从法律角度来看，需要政府相关部门制定一系列隐私安全保护方面的法律法规，通过这些法律法规对发布的数据形式进行约束；技术的研究大多集中于针对于单敏感属性的隐私保护的研究。例如，利用(p,a)-sensitivek-匿名模型，让每个等价类的元组个数大于或等于k；每个敏感属性值的数量大于或等于p，从而对l-多样性模型中的参数设置进行优化。该模型的缺点是由于没有对各个等价类的敏感值频率进行约束，在p远远小于k小时，该模型不能有效地抵御偏斜性攻击[1]。因此，有学者提出了(a,k)-匿名模型，改进了(p,a)-sensitivek-匿名模型存在的问题。模型提出利用频率参数对等价类的敏感属性出现的频率进行约束，在一定程度上阻止攻击者进行同质攻击[2]。针对单敏感属性的研究有许多经典的模型，例如，k-匿名模型[3]；A.Machanavajjhala等[4]于2006年首次提出的l-多样性模型；文献[5]提出的t-逼近模型等。

围绕多敏感属性的隐私保护的研究较少。文献[6]利用多维桶结构，在分组过程中，将复合敏感属性的每一维分别与多维桶的各维对应。将实验数据集的元组根据高维敏感属性向量映射到对应的桶中，然后依据特定隐私保护原则在多维桶中选择符合要求的元组构成分组，确保在最终构成的分组中每一维敏感属性上的取值都符合特定的隐私保护原则，从而确保多维敏感属性数据发布的安全性。有一些学者提出其他模型来解决多敏感属性的隐私保护，例如，文献[7]提出了个性化分级(l,a,m)-多样性匿名模型；文献[8]提出了最小选择度优先的多维敏感属性个性化。由于有损分解会破坏数据之间的关系，文献[9]提出了msa(multiple sensitive attributes)l-maximum算法。

本文研究了已有的多敏感性数据隐私保护算法，对多维桶分组技术存在的不足展开分析，提出一种基于多敏感属性相关性划分的(m,l)-匿名隐私保护模型(记为SCPLCG)，给出多敏感属性相关性计算的方法，阐述模型基本定义，再采用聚类算法对敏感属性满足(m,l)-diversity进行分组，保证发布的数据可以防止偏斜性攻击，也能够抵御一定程度的背景知识攻击，最终减小匿名数据的附加信息损失和隐匿率，保证数据发布的可用性。

1 匿名隐私保护模型

1.1 敏感属性相关性划分

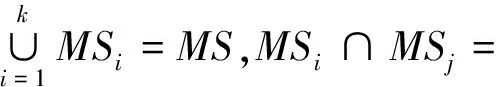
利用信息增益法[10]计算任意2个敏感属性的相关性。具体定义如下。

在数据集S中，任意的A和B2个敏感属性，其中敏感属性A的值域表示为{a1,…,ai,…,an}，1≤i≤n；敏感属性B的值域表示为{b1,…,bj,…,bm}，1≤j≤m。

定义1.2 条件熵。在数据集S中，敏感属性B的条件下敏感属性A的条件熵定义为

(1)

(1)式中：

(2)

(3)

(4)

(1)—(4)式中：p(ai|bj)表示已知敏感属性B的条件下敏感属性A的后验概率；sumij表示数据集sumj中s[A]=ai且s[B]=bj的元组总数；sumj表示S中s[B]=bj的元组的总数。

定义1.3 信息熵。在数据集S中，敏感属性A的信息熵定义为

(5)

(5)式中：

(6)

(6)式中：p(ai)表示敏感属性A取值ai的先验概率；sumi表示S中s[A]=ai的元组总数；|S|表示S中所有元组的总数。

定义1.4 信息增益。在数据集S中，敏感属性A的信息熵的相对减少量被称为信息增益，定义为IG(A|B)=H(A)-H(A|B)。

定理1.1 信息增益具有对称性和非负性，IG(A|B)=IG(B|A)且IG(A|B)≥0。

对此进行证明

同理可证

由此推导出：IG(A|B)=IG(B|A)；

由上述公式继续推导

根据不等式lnx≤x-1，x>0，且有lbx=lnxlbe，推导出

综上，证得：IG(A|B)≥0。

在计算出属性间的相关性之后，使用聚类方法对属性进行划分。设A，B是任意2个敏感属性，A，B之间的距离为

(7)

若敏感属性A和B间的相关性越强，则二者之间的距离就越近。

定理1.2 相异矩阵。在数据集S中，m维敏感属性S1,S2,…,Sm间的相异矩阵定义为

(8)

本文采用基于密度信息的改进k-中心点算法对多敏感属性相关性划分。算法步骤如下。

步骤1 计算得到敏感属性间的距离并和相异矩阵；

步骤2 设置阈值minPts，高于minPts的样本选取为高密度样本；

步骤3 在高密度样本中选取密度最高的样本点作为第1个初始中心点，选择距离第1个初始中心点最远的样本点作为第2个初始中心点，再选择距离第1个和第2个初始中心点最远的样本点作为第3个初始中心点。以此类推，选取出k个初始中心点为止；

步骤4 形成簇。把除了中心点之外的样本点，划分到距离最近的中心点，形成簇，接着循环交换中心点与任意非中心点，并重新聚类直到聚类代价不再下降，其中聚类代价设定为每个点到最近中心点距离的总和。

由于本文将数据发布中的敏感属性作为聚类空间中的点，通常敏感属性的维数不会太大，因而该算法不会受到高复杂度的影响。

1.2 模型的基本定义

在模型中用到的基本定义如下。

定义1.5 多敏感属性(m,l)-diversity。在数据集S中，一个含有m条元组的分组W，如果要删除W中所有元组，则需要至少删除l个不同的敏感值属性。

定义1.6 删除。设W是数据集S的一个分组，如果要将W中任意一条元组的某一个敏感属性值从W中删除，则需要将W中包含这个敏感属性值的所有元组删除。

定义1.7 相同敏感属性值集合。在数据集S中，每一维敏感属性上的敏感值都相同的元组组成的集合记为C(v)。

定义1.8 多敏感属性(m,l)-diversity分组。对于数据集S上的分组GS={G1,G2,…,Gn}，若任意分组Gi(1≤i≤n)都满足多敏感属性(m,l)-diversity原则，则GS是S上满足(m,l)-diversity原则的分组。

多敏感属性数据如表1所示。

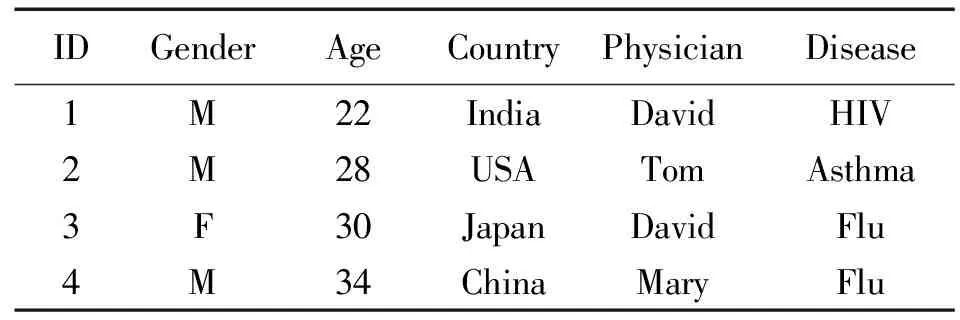
表1 多敏感属性数据表Tab.1 Data table of multi-sensitive attribute

在表1中，若要删除表中的所有记录，则只需将敏感属性值David和Flu删除即可，可以满足多敏感属性(m,l)-diversity性质，同时，可以得到满足多敏感属性(m,l)-diversity的匿名数据表。

若采用最大桶分组技术则得到的匿名如表2所示。

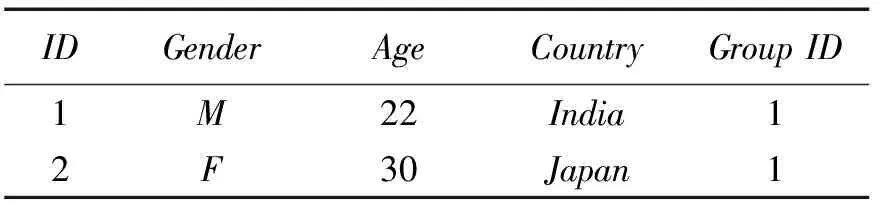
表2 满足最大桶分组技术的匿名数据表Tab.2 Anonymous data table of the largest bucket grouping technique a 准标识符属性

b 敏感属性

通过分析对比表1和表2可知，采有多维桶分组技术会导致更多的元组被隐匿，降低了数据的效用。满足多敏感属性(m,l)-diversity原则进行分组，分组中敏感属性间的值存在对应的多样性。因此，多敏感属性(m,l)-diversity分组能够在一定程度上降低背景知识攻击的风险。

基于以上分析，为了增强模型的保护强度，对参数m和l进行条件约束如下。

1)m≥l≥2，这是构成分组的必要条件；

2)m≤2(l-1)，当一个分组含有m条元组，需要删除l个不同的敏感属性值才能将该分组删除，当这个分组存在这种最坏分布情况：要删除的这l个不同敏感值属性值包含l-1个不同敏感属性值，同时还包含不同于这l-1个的敏感属性值，且具有该值的元组共有m-(l-1)个。为了防止偏斜性攻击，m-(l-1)要小于l-1，即含有该敏感属性值的元组个数不能超过该分组总数的一半。该约束条件限制分组中任意敏感属性值出现的频率不超过0.5。

1.3 隐匿数据评估标准

对于隐匿数据的评估主要包含附加信息损失和隐匿率2个标准，具体如下。

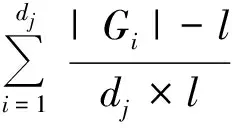
(9)

(9)式中，c为敏感属性的个数。

定义1.10 隐匿率。若一条元组存在一个或多个敏感属性值被隐匿，则该元组就被视为隐匿元组。假设数据集S中有ns条元组被隐匿，则隐匿率定义为

(10)

2 算法实现

2.1 基于密度信息的改进k-中心点算法

输入：n维敏感属性表MS={S1,S2,…,Sn}和k个簇；

输出：k个子敏感属性表MS={MS1,MT2,…,MTk}。

1)利用信息增益计算出敏感属性之间的相异矩阵D；

2)将每一维敏感属性看作一个样本点，计算所有距离的平均值一半作为样本点领域半径r；

3)计算每个样本点r邻域内样本数，将所有样本数的平均值作为高密度点样本应该包含最少样本数的阈值minPts；

4)将所有r邻域内含有邻居样本点个数不少于minPts的样本点加入到集合W中，从而构成高密度样本集合；

5)选取初始中心点集合C

①W中选取密度最高的样本点c1作为第1个初始聚类中心加入集合C；

②从W中选取距离c1最远样本点c2作为第2个初始聚类中心加入集合C；

③从W中选取距离c1,…,ck-1之和最远的样本点ck作为第k个初始聚类中心加入集合C；

6)循环接下来的过程，直到中心点不在发生变化

①将余下的n-k个样本点依照距离划分到离它最近的中心点；

②选择某个中心点ci与任意一个非中心点c′交换，重新聚类并计算聚类代价，若划分到该中心点的样本点至少有一个且能使聚类代价下降，则用c′替换ci。

7)输出k个子敏感属性表。

在源代码的基础上分析算法2.1的时间复杂度。步骤1，获取相异矩阵花费时间为O(n2)；步骤2，计算样本点领域半径花费时间为O(n2)；步骤3，计算样本数的阈值花费时间为O(n2)；步骤4，构成高密度样本集合花费时间为O(n)；步骤5，选取初始中心点集合花费时间为O(k)；步骤6，调整中心点花费时间为O(k(n-k))。所以，整个执行过程所花费的总时间为O(n2)。

2.2 基于聚类的(m,l)-diversity分组算法

从2.1节得到k个子敏感属性表，2.2节对每个子敏感属性表进行满足(m,l)-diversity原则分组。

输入：数据表S={QI1,QI2,…,QIm,MS1,MS2,…,MSk}，多样性参数l；

输出：准标识符属性表QIT，敏感属性分组表GST。

1)于任意子敏感属性表MSi，将元组在MSi上构造相同敏感属性值集合{C1(v),C2(v),…,Cn(v)}，将集合按照从大到小的顺序排列；

2)while(可以提取元组构成分组)

①设分组W=φ，从最大集合中随机选取一条元组添加到分组W中，将该元组从此集合中删除；

②while(W的元组个数小于l)

筛选符合元组t添加到分组W中满足复合敏感属性m-(l-1)原则的集合，从这些集合中选取最大集合中的一条元组添加到W中，将该元组删除；

endwhile；

endwhile；

3)foreach剩余元组rt

若存在分组W′，添加rt后仍满足复合敏感属性l-diversity原则，且m≤2(l-1)，则将rt添加到W′，并删除该rt；

endfor；

4)foreach剩余元组rt′

若存在分组W′，添加rt′后满足多敏感属性(m,l)-diversity原则，且m≤2(l-1)，则将rt′添加到W′，并删除该rt；

endfor；

5)将无法加入任意分组中满足多敏感属性(w,l)-diversity原则的元组隐匿；

6)将所有分组以准标识符属性表QIT和敏感属性分组表GST的形式发布。

在源代码的基础上分析算法2.2的时间复杂度。假设原始数据集T中元组数量为m，分组个数为k，且1≤k≤m/l。步骤1，构造相同敏感属性值集合花费时间为O(m)；步骤2，完成分组花费时间为O(lkm)；步骤3，添加剩余元组满足复合敏感属性l-diversity原则花费时间为O(k(m-lk))；步骤4，满足多敏感属性(p,l)-diversity原则花费时间小于O(k(m-lk))；步骤5，匿名处理剩余元组花费时间小于O(kl)。所以，整个算法执行所花费的总时间不超过O(m2)。

3 实验结果及分析

3.1 实验数据集

本文的实验数据集来自UCI机器学习数据库中的Census-Income，在预处理中，删除了有缺损信息的数据，随机选取了9 000条数据构成实验数据集。

本文选取其中7个属性，数据集的结构描述如表3所示，将数值型属性数据离散化处理，划分成区间形式并视为分类型属性。

表3 Census-Income数据集结构Tab.3 Data set structure of Census-Income

实验将从匿名数据集对于隐匿率和附加信息损失度两方面考查本文提出的算法性能，并与多维桶分组技术中的最大桶第一(maximal-bucket first，MBF)算法进行对比。实验从以下2个方面对算法进行分析对比：①变化的多样性参数取值l(l取值为3～8)；②变化的敏感属性个数c(c的取值为4～7)，如表4所示。

表4 实验中使用的多敏感属性Tab.4 Multi-sensitive attributes used in the experiment

3.2 隐匿率分析

图1和图2对SCPLCG和MBF这2种算法产生的隐匿率情况进行了对比。图1表明在敏感属性的维数为c=5情况下，2种算法在多样性参数l取值不同时产生的隐匿率。从图1—图2中可以得知，MBF算法产生的隐匿率要高于SCPLCG算法。原因在于当敏感属性的维数较高时会导致敏感属性间的限制越来越多，并且MBF算法在分组的过程中必须满足l-diversity分组，任意2个元组只要在某一维上的敏感属性值相同就不能被分到一个组中，这极大地增加了分组的难度。对于SCPLCG算法而言，虽然敏感属性的维数较高，但将敏感属性进行相关性划分为几个子敏感属性表，直接降低了分组的敏感属性维数，使敏感属性在分组过程中受到的限制减小，增加了分组的成功率。另外，当l值逐渐增大时，要满足分组原则进行分组的难度加大，2种算法的隐匿率都增大，但是SCPLCG算法满足(m,l)-diversity分组原则，没有MBF算法分组条件严苛。因此，MBF隐匿率增大的幅度要大于SCPLCG。

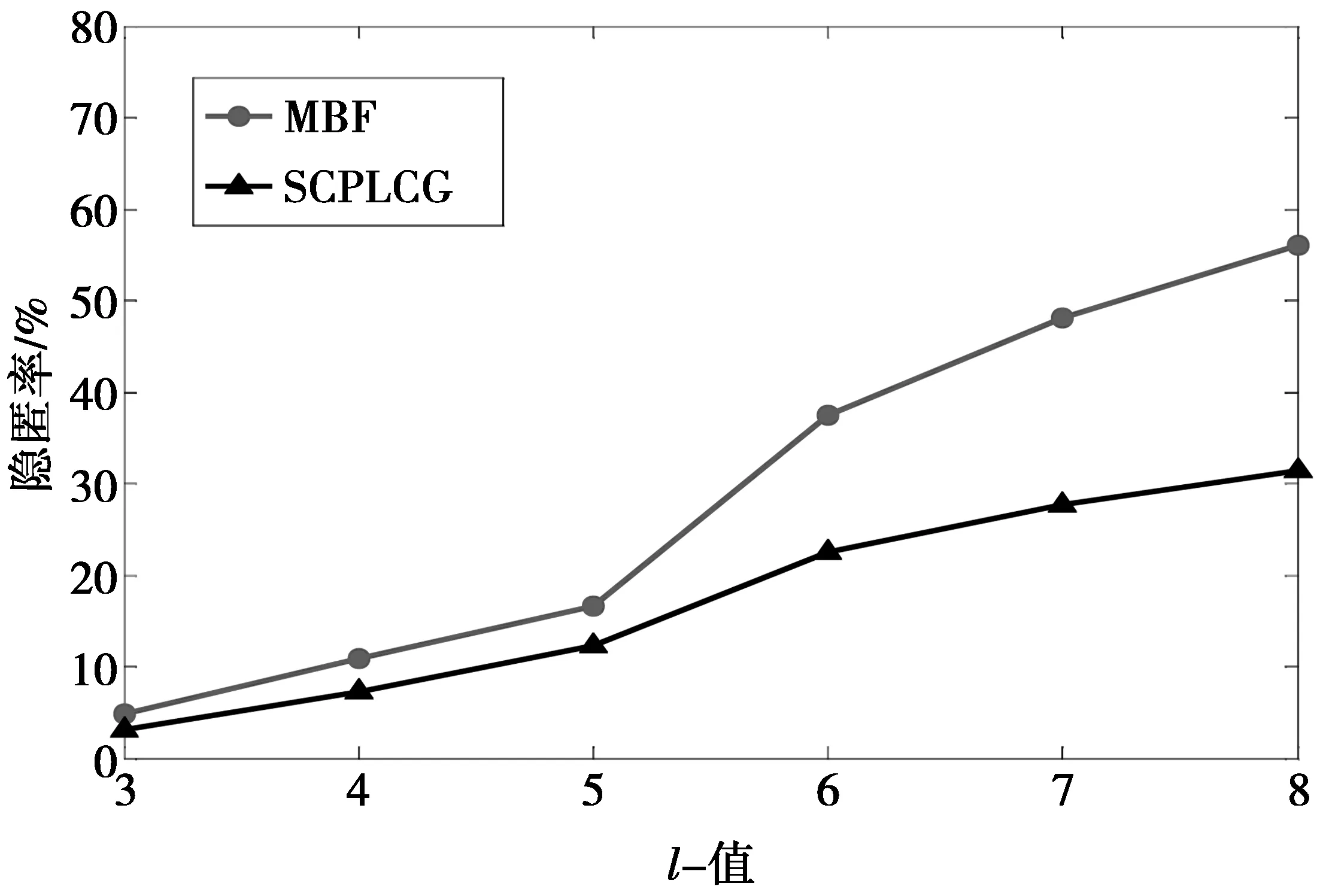
图1 多样性参数l值变化下的隐匿率比较 (c=5)Fig.1 Comparison of occultation rate under variation of diversity parameter l(c=5)

图2表明，在多样性参数l=3情况下，2种算法在敏感属性维数取值变化时产生的隐匿率。从图2中可以看出，MBF算法的隐匿率要大于SCPLCG，这是由于SCPLCG算法通过对敏感属性划分，很好地降低了敏感属性维数，并且满足(m,l)-diversity分组原则进行分组的元组更多。当敏感属性维数增大时，2种算法的隐匿率都増大，原因在于敏感属性的维数越多，得到在每一维上的分组就越困难。整体而言，在多样性参数取值不大时，二者产生的隐匿率都比较小。

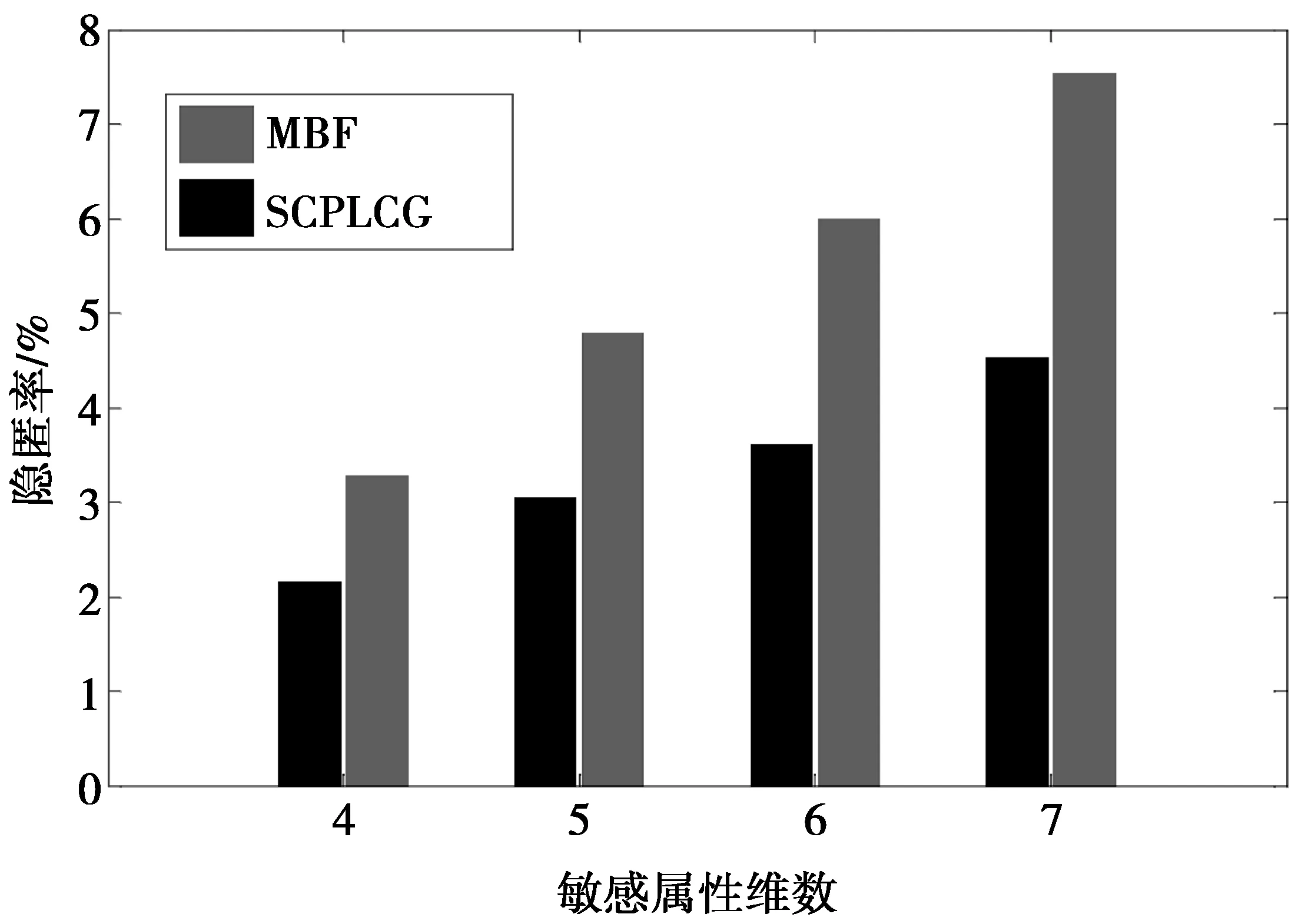
图2 敏感属性维数变化下的隐匿率比较 (l=3)Fig.2 Comparison of concealment rate under the change of sensitive attribute dimension(l=3)

3.3 附加信息损失分析

图3和图4对SCPLCG和MBF 2种算法产生的附加信息损失度情况进行了对比。图3表明在敏感属性维数为c=5情况下，2种算法在多样性参数l取值变化时产生的附加信息损失度。从图3中可以得知，随着l值的增大，2种算法产生的附加信息损失度都会增大。由于增大l值会使隐匿的元组増多，构成的分组总数变少，导致计算附加信息损失度公式中的分母值变小，间接的增大了附加信息损失度。同时，在l值较小时，MBF的附加信息损失度要高于SCPLCG，这是因为SCPLCG算法将敏感属性划分为多个子表，降低了分组的敏感属性维数，同等条件下构成的分组要比MBF多。当多样性参数l取值为7，8时，SCPLCG算法产生的附加信息损失度略高于MBF，这是由于满足l-diversity分组的难度加大，剩余元组增多，但从算法的执行过程来看，SCPLCG算法在满足l-diversity形成分组后，在处理剩余元组时没有MBF算法条件严苛，会有更多的元组满足(m,l)-diversity原则添加到分组中，导致计算附加信息损失度时的分子值变大，间接的增大附加信息损失度。

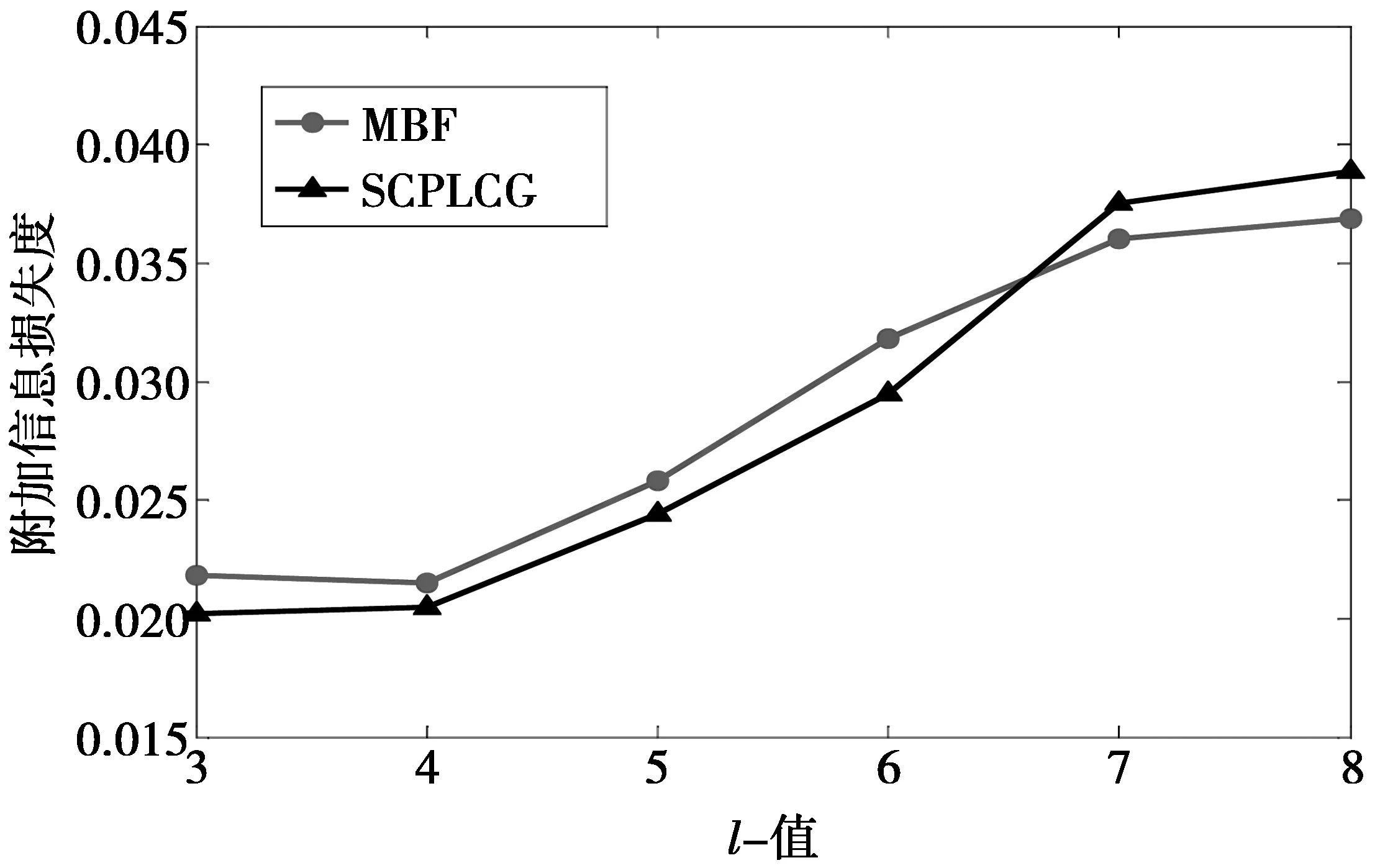
图3 多样性参数l值变化下的附加信息 损失度比较(d=5)Fig.3 Comparison of additional information loss under variation of diversity parameter l(d=5)

图4表明在多样性参数为l=3情况下，2种算法在敏感属性维数取值变化时产生的附加信息损失度。从图4中可以看出，MBF算法的附加信息损失度要略大于SCPLCG，这是由于SCPLCG算法通过对敏感属性划分，很好地降低了敏感属性维数，满足l-diversity形成分组的元组更多。另外，当敏感属性维数增加时，2种算法的附加信息损失度都有所増大。这是由于敏感属性的维数越大时，得到在每一维敏感属性上的分组就越困难。整体而言，2种算法产生的附加信息损失度都比较小。

图4 敏感属性维数变化下的附加信息 损失比较(l=3)Fig.4 Comparison of loss of additional information under the change of sensitive attribute dimension(l=3)

4 结束语

本文研究了基于有损连接的多维桶分组技术，对其中存在的缺陷进行分析，提出了一种基于多敏感属性相关性划分的(p,l)-匿名隐私保护模型。给出敏感属性相关性计算方法和基于聚类的相关性划分算法，阐述了模型的分组原理和相关定义，分析模型的安全性。最后，给出了该模型的实现算法，并使用真实数据集进行实验仿真分析。实验结果表明，基于多敏感属性相关性划分的(p,l)-匿名隐私保护模型具有较小的附加信息损失和隐匿率，保证了发布数据的可用性。

下一步的研究工作主要是针对动态数据进行隐私保护。在发布的数据时刻变动的应用场景中，隐私保护研究变得更加复杂，难度也更大，如何针对动态数据进行有效的数据发布匿名隐私保护是未来研究的重点。

[1] TRUTA T M, VINAY B. Privacy protection: p-sensitive k-anonymity property[C]//Proceedings of the 22nd International Conference on Data Engineering Workshops. Washington: IEEE, 2006: 94-104.

[2] WONG R C W, LI J, FU A W C, et al. (α, k)-anonymity: an enhanced k-anonymity model for privacy preserving data publishing[C]//Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining. New York: ACM, 2006: 754-759.

[3] SWEENEY L. k-anonymity: A model for protecting privacy [J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(5): 557-570.

[4] MACHANAVAJJHALA A, KIFER D, GEHRKE J, et al.l-diversity: Privacy beyond k-anonymity [J]. ACM Transactions on Knowledge Discovery from Data (TKDD), 2007, 1(1): 24-35.

[5] LI N, LI T, VENKATASUBRAMANIAN S.t-closeness:Privacy beyond k-anonymity andl-diversity[C]//Proceedings of IEEE 23rd International Conference on Data Engineering (ICDE 2007).Istanbul: IEEE, 2007: 106-115.

[6] 杨晓春,王雅哲,王斌,等.数据发布中面向多敏感属性的隐私保护方法[J].计算机学报, 2008, 31(4): 574-587. YANG Xiaochun, WANG Yazhe, WANG Bin, et al. Privacy Preserving Approaches for Multiple Sensitive Attributes in Data Publishing [J]. Journal of Computer Science, 2008, 31 (4): 574-587.

[7] 刘志军,张艳丽,闫晶星,等.面向多敏感属性的个性化分级(l,a,m)-多样性匿名方法[J].科技通报, 2016, 32(1):123-127. LIU Zhijun, ZHANG Yanli, YAN Jingxing, et al. An Personalized Classification (l,α,m)-diversity Anonymous Approach for Multi-sensitive Attributes [J]. Journal of science and technology, 2016, 32(1):123-127.

[8] 张冰,杨静,张健沛,等.面向敏感性攻击的多敏感属性数据逆聚类隐私保护方法[J].电子学报, 2013, 42(5): 896-903. ZHANG Bing, YANG Jing, ZHANG Jianpei, et al. A Multi Sensitive Attribute Data Inverse Clustering Privacy Preserving Algorithm for Sensitivity Attack [J]. Journal of Electronics, 2013, 42(5): 896-903.

[9] 谢静,张健沛,杨静,等.基于属性相关性划分的多敏感属性隐私保护方法[J].电子学报, 2014, 42(9): 1718-1723. XIE Jing, ZHANG Jianpei, YANG Jing, et al. A Privacy Preserving Approach Based on Attributes Correlation Partition for Multiple Sensitive Attributes [J]. Journal of Electronics, 2014, 42(9): 1718-1723.

[10] DAI Jianhua, XU Qing. Attribute selection based on information gain ratio in fuzzy rough set theory with application to tumor classification [J]. Applied Soft Computing, 2013, 13(1): 211-221.

(编辑：刘 勇)

s：The Key Project of Chongqing Education Science in 12th Five-Year; The Chongqing Outstanding Achievement Transformation Project(KJZH17116); The Chongqing Municipal People’s Livelihood Science and Technology Innovation(cstc2016shmszx40001)

In the data publishing process, if the sensitive attribute information is released without any protection processing, it will be vulnerable to be attacked, which leads to the leakage of privacy information. In this paper, since the traditional single-sensitive attribute privacy protection methods do not perform well in the multi-sensitive attributes scenarios, an anonymous privacy protection model based on multi-sensitive attribute relevance partitioning is proposed. First, the information gaining method is used to calculate the correlation of multi-sensitive attributes, and the dimension of sensitive attributes is reduced. Then, sensitive attributes are grouped according to the (m,l)-diversity principle to ensure that the published data can prevent skew attacks, and to a certain extent ,the risk of background knowledge attack is reduced. Finally, this model is implemented by clustering technique to reduce the additional information loss and concealment rate of the model and ensure the high availability of the published data. The experimental results show that the anonymity privacy protection model based on multi-sensitive attribute correlation has smaller additional information loss and concealment rate, which ensures the availability of published data.

multi-sensitive attributes; anonymity; clustering; information

10.3979/j.issn.1673-825X.2017.04.018

2016-10-19

2017-03-20 通讯作者：张荣庆 botherdog929@163.com

重庆市教育科学“十二五”规划重点课题;重庆市高校优秀成果转化资助(KJZH17116);重庆市社会民生科技创新专项(cstc2016shmszx40001)

TP393

A

1673-825X(2017)04-0542-08

Method of anonymous privacy preserving for multi-sensitive attributes

(1. School of Computing and Information Science, Southwest University, Chongqing 400065, P. R. China;2. Chongqing Bashu Secondary School, Chongqing 400013, P. R. China;3. School of Software Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, P. R. China;4. Postdoctoral Station of Information and Communication Engineering, Chongqing University, Chongqing 400044, P. R. China)

张荣庆(1975-)，男，重庆人，中学高级教师，在职硕士研究生。主要研究方向为现代教育技术及网络信息安全。E-mail：botherdog929@163.com。

徐光侠(1974-)，女，重庆人，教授，博士，硕士生导师。主要研究方向为大数据分析与安全、网络安全与管控、 物联网安全等。E-mail：xugx@cqupt.edu.cn。

ZHANG Rongqing1,2, XU Guangxia3,4