面向单目标优化的集成粒子群算法

何 莉，王 淼，李 博

(河南工程学院 计算机学院, 郑州 451191)

面向单目标优化的集成粒子群算法

何 莉，王 淼，李 博

(河南工程学院 计算机学院, 郑州 451191)

串行粒子群算法广泛应用于多个领域，出现了多个变种，但解决不同种类的优化问题时性能有差异。为提高串行粒子群算法对各种优化问题的适应能力，提出一种集成粒子群优化算法。新算法使用Matlab的单程序多数据并行结构发挥单节点多核计算能力，通过设置外部档案分享不同粒子群的全局最佳位置，促进不同串行粒子群算法之间的信息交流，综合利用不同串行粒子群算法在解决不同类型优化问题的优势。在广泛使用的测试函数集上开展仿真实验，结果验证了新算法的有效性，与多个知名的串行粒子群算法相比，新算法在寻优性能上优势明显。新算法不仅能够提高粒子群算法的适应能力，而且，所采用的算法框架也适应于其他群智能算法，改善了算法的性能。

单程序多数据；集成粒子群算法；全局数值优化；粒子群优化；并行计算

0 引 言

现实世界中工程和科学问题很多可以抽象为单目标优化问题。如果目标函数和约束条件是决策变量的线性组合，可以用经典的线性规划、动态规划等方法解决。然而，现实世界的优化问题经常是非线性的，维数比较高，用经典方法并不能取得较好的效果。启发式算法借鉴自然进化思想，在解决复杂优化问题时取得显著成效，也受到学术界高度关注和追踪[1]。典型的启发式算法包括粒子群算法[2]、蚁群算法[3]、人工蜂群算法[4]、萤火虫算法[5]等。

粒子群算法(particle swarm optimizer，PSO)出现于1995年[2]，受到鸟类觅食群体行为的启发。粒子群算法包括多个粒子，每个粒子对应优化问题的一个解。粒子的位置初始化后，其移动轨迹受到粒子自身最佳位置以及邻域中粒子最佳位置的影响，粒子的行为决定于自身的惯性和社会行为。PSO算法最早应用于神经网络的参数优化。由于PSO算法的简洁性和方便处理高维优化问题的能力，PSO算法已广泛应用于多个领域[6-8]。

现有多数PSO算法的代码以串行方式执行，称这类PSO为串行粒子群算法(serial particle Swarm optimizer，SPSO)。SPSO在处理优化问题中取得显著成绩，但依然存在多个问题需要解决，比如迭代寻优的耗时问题，大数量级数据处理问题，自身行为与社会行为的主导性问题，探索与挖掘矛盾的处理。现已提出多种并行与分布式PSO[9-11]用于解决前2个问题。粒子的行为轨迹受到自身历史最佳位置和邻域粒子的影响，如何更有效地引导粒子下一步动作值得进一步研究。粒子的通信拓扑被认为是刻画粒子与邻域关系的有效方法，被广泛使用的拓扑结构有全连接[12]和环型拓扑结构[13]。文献[14-15]认为粒子的行为受到其邻域中所有粒子的影响，粒子群进行探索的目的是跳出局部最优解，在更大的区域寻找全局最优解，粒子群进行挖掘的目的是对局部区域进行细粒度搜索更优解。反向学习机制被引入提高粒子的学习能力[16-17]，核矩阵被用于改善粒子的多样性[18]。多种参数约束的SPSO算法已提出用于折衷探索与挖掘的关系[12, 19-22]，每种SPSO算法在解决特定优化问题时都有较好的表现。

为融合各种SPSO算法在解决不同类型问题的优势，提出一种集成粒子群算法(ensemble particle swarm optimizer, EPSO)。EPSO采用Matlab单程序多数据(single program multiple data，SPMD)并行结构，利用单节点多核的并发处理能力，用多个内核分别运行全局粒子群算法(global PSO，GPSO)[12]，本地粒子群算法(local PSO，LPSO)[13]，裸骨粒子群算法(bare bones particle swarms，BBPSO)[23]和全信息粒子群算法(fully informed particle swarm，FIPS)[14-15]，然后，通过信息共享机制促进粒子群全局最佳位置的共享，提高PSO算法的准确性。

EPSO算法提出的主要思想：通过并行化方式不仅实现不同粒子群算法的协同进化，而且，还融合了各自算法的优势，是提高粒子群算法性能的新方法。

1 串行粒子群算法

一个粒子群由S个粒子构成。每个粒子用序号表示，第k个粒子用粒子k表示。粒子k的状态由位置向量Xk和速度向量Vk来表示。在D维空间中，Xk=[xk1,xk2,…,xkD]，Vk=[vk1,vk2,…,vkD]。粒子k的个体最佳位置和邻域最佳位置分别用Pk和Lk表示，即Pk=[pk1,pk2,…,pkD]，Lk=[lk1,lk2,…,lkD]。粒子群全局最佳位置用G表示，即G=[g1,g2,…,gD]。对于最小化问题，最佳位置意味着在指定的范围该位置的适应度最低。粒子k的邻域Nk由粒子群的通信拓扑决定，对于环型通信拓扑结构，粒子k的邻域包括粒子k-1，k和k+1，即Nk={k-1,k,k+1}。

LPSO[13]中Xk和Vk在随机初始化后，分别按照(1)和(2)式进行更新。

(1)

(2)

(1)—(2)式中：ω表示惯性系数，通常被设置为随迭代次数逐渐减少的值，比如文献[12]建议ω由0.9降低到0.4；c1和c2分别表示界定认知部分与社会部分贡献的加速系数，在不同SPSO算法中，c1和c2取值有所不同，比如文献[12-13]中，c1和c2被设置为2.0；r1d和r2d是[0, 1]上的随机数，服从均匀分布，为粒子的速度更新带来一定的随机性。

GPSO[12]中粒子的邻域包含粒子群中所有粒子，粒子的位置根据(2)式进行更新，但是粒子的速度根据(3)式进行更新。因此，GPSO可以看成是LPSO的一个特例。

(3)

为解决SPSO在求解多模优化问题容易陷入局部最优而导致过早收敛的问题，算法CLPSO[24]提出了一种深度学习策略，即粒子每维速度的更新受到其他所有粒子个体历史最佳位置的影响，粒子速度的更新公式为

(4)

(4)式中，f(k)表示引导粒子k在第d维运动的粒子的序号。

FIPS[14-15]认为粒子位置的变化受到邻域所有粒子历史最佳位置的影响，其速度更新采用的公式为

(5)

(5)式中：rd表示区间(0,φ)上的随机数，服从均匀分布，参数φ通常被设置为4.1；此时，χ≈0.729 8[15]。FIPS[15]可以看成是文献[19]提出的PSO算法的通用版。

标准的粒子群算法存在多个参数，参数的设置会影响到算法执行的效果。算法BBPSO[23]去掉了速度更新公式，粒子位置的更新公式为

(6)

(6)式中：μkd←0.5(pkd+lkd)；σkd←|pkd-lkd|；N(μkd,σkd)是以μkd为均值和σkd为方差的高斯分布的一个值。BBPSO以其简洁性受到关注，在此基础上又发展了文献[25]提出的算法。

粒子群的变种还有很多，文献[6]综述了粒子群算法的各个变种以及应用。不同粒子群算法各具有优势。GPSO[12]和LPSO[13]运行速度比较快，在单模优化问题上有优势，而FIPS[14-15]和BBPSO[23]在解决多模优化问题时取得良好的结果。

2 集成粒子群算法(EPSO)

每种SPSO算法在解决某一类优化问题有优势，比如GPSO[12]适合解决单模单目标优化问题；综合学习粒子群算法(comprehensive learning，CLPSO)[24]在解决多模单目标优化问题时比其他PSO算法表现更好。没有免费午餐(no free lunch，NFL)理论[14]表明，没有一种算法在评测所有可能的优化函数时都优于其他算法。为了提高SPSO算法对不同优化问题的适应能力，有必要综合各种算法的优势。

2.1 Matlab SPMD并行结构

在单核CPU时代，多线程技术用于减少CPU的等待时间，提高CPU的利用效率。由于CPU同一时刻只能执行一个线程，单核多线程并不是真正意义上的并行计算。进入多核时代，多个线程可以分配给多个内核同时运算，实现并行计算，此时，多线程编程也称为多核编程。

Matlab提供2种方式利用多核计算能力：①内置多线程，快速傅立叶变换(fast Fourier transform，FFT)、矩阵特征值和特征向量函数eig、奇异值分解函数svd、排序函数sort等线性代数和数值函数在Matlab上执行时默认启用多线程，图像处理工具箱中许多函数也默认启用多线程；②基于Matlab工作单元(worker)的并行计算，Matlab启用多个工作单元实现应用的并行执行。②相对于①的优势是对并行计算有更多的控制，可以将并行应用由单个节点扩展到集群。②通常采用2种编程结构：parfor和SPMD[26]。parfor主要实现for循环的并行运算，SPMD并行结构比parfor并行结构更灵活，但也引入更加复杂的数据类型和操作方法。

Matlab SPMD并行结构如图1所示。客户端(client)完成所有的用户交互操作，并提交任务给调度器(scheduler)；调度器负责Matlab工作单元的管理，并将任务分解为多个作业，每个作业由调度器分配给工作单元执行；工作单元执行作业，并将执行结果返回。客户端、调度器、工作单元既可以运行在单个节点，也可以运行在多个节点。本文侧重于单节点多核计算。

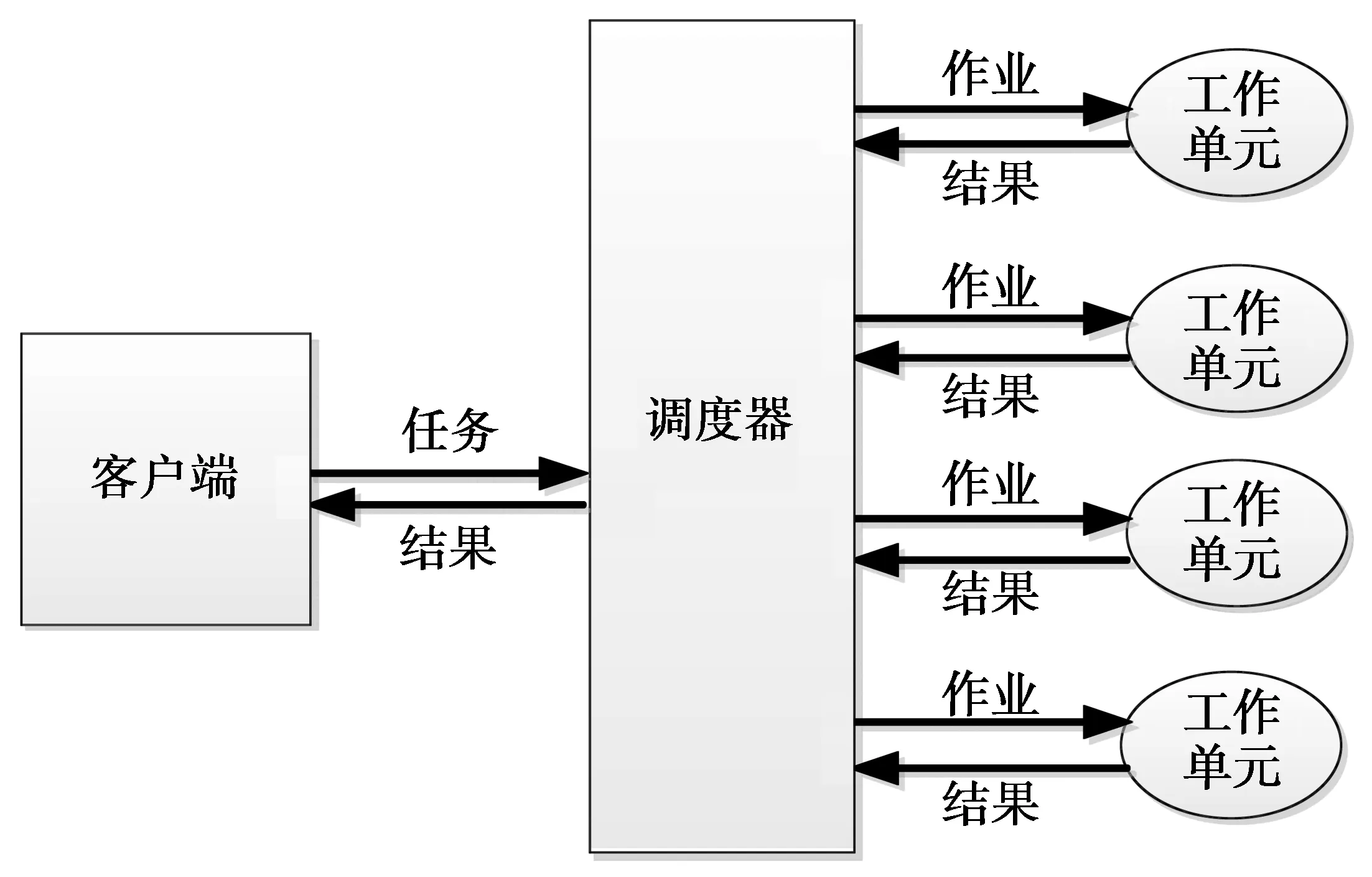
图1 Matlab SPMD并行结构Fig.1 Matlab SPMD parallel structure

2.2 并行策略与信息共享

在异构分布式计算环境时，计算效率的提升除了与节点自身计算资源相关外，也受到节点之间通信资源的影响。在单节点多核并行计算环境中，多个内核之间通信速率通常远高于节点之间通信速率，所以多核计算效率的提升主要与自身的计算资源关系密切。

EPSO算法中，客户端主要负责参数初始化、并行任务的启动、结果汇总等工作。一个工作单元对应一个内核，执行单个SPSO算法，维护一个粒子群的状态信息，算法开始后每隔一定迭代次数，通过工作单元间通信机制将各个SPSO的最佳位置存放在档案中。各个SPSO的粒子群构成一个粒子群集合。

粒子群信息的交流已被证明能够有效提高粒子的多样性和增强避免陷入局部最优解的能力[27-28]。在EPSO算法中，每个工作单元设置并维护一个档案，用于存放并行执行阶段各个SPSO算法的粒子群全局最佳位置，适应度最小(对于最小优化问题)的粒子群全局最佳位置将作为粒子群集合的最佳位置best_G。因为进入并发执行阶段，不同的SPSO算法执行的速度有快有慢，所以各个SPSO经过相同的迭代次数，计算的best_G可能不一样。这体现了EPSO同一个粒子群内同步通信而不同粒子群间异步通信的特点。通过信息共享，实现最佳位置在多个粒子群中共享。通过档案传递粒子群的最佳位置的速度高于文献[29]提到岛屿模型(island model)。在岛屿模型中，多个粒子群按序排列，逐个向下一个粒子群传递最佳位置。

EPSO算法采用随机替换策略实现SPSO的粒子群与粒子群集合的最佳位置的交流。SPSO计算best_G后，产生一个服从均匀分布的序号，然后将序号对应的粒子的个体最佳位置替换为best_G，使得粒子群受到best_G的影响，提高找到更优解的可能性。这种替换策略简单有效，不会改变SPSO原有的粒子速度和位置的更新公式。

2.3 EPSO的实现流程

目前，楚雄市汉语公示语英译的数量远远不够，很多对外交流频繁的地方还缺少公示语的翻译，例如公共汽车站，火车站售票窗口，彝族文化活动场所，市区主干道的景区标识牌，还有一些功能性建筑物都缺少规范的公示语翻译，城市的对外文明形象也大大削弱了。

EPSO的实现流程如图2所示，程序分为3个阶段进行。

图2 EPSO算法流程Fig.2 Flow chart of EPSO algorithm

1)程序采用串行执行方式，即由系统选择一个内核顺序执行指令，客户端完成粒子群粒子数量，加权系数ω，控制系数c1，c2，迭代次数等算法参数的初始化，以及启动4个内核作为并行工作单元。

2)程序采用并行执行方式。4个并行工作单元分别执行SPSO算法GPSO[12]，LPSO[13]，BBPSO[23]和FIPS[15]，对应的粒子群全局最佳位置分别用GPSO_G，LPSO_G，BBPSO_G，FIPS_G表示。每种SPSO算法每经过step次迭代，通过工作单元间的通信机制收集4个粒子群的全局最佳位置，并计算best_G，然后，从自身粒子群中随机选取一个粒子，将其个体最佳位置替换为best_G。

进入并行执行阶段后，Matlab调度器负责工作单元的管理和作业的分配。

3)程序采用串行执行方式。当所有作业完成后，进入串行执行阶段。客户端收集各个算法的最佳位置，并计算best_G，作为优化问题的最终解。

3 实验与讨论

3.1 评测函数

实验采用CES’15[30]评测集。评测集共有15个单目标最小优化函数，分为4种类型，其中，F1(x)和F2(x)是单模函数，F3(x)～F5(x)为简单多模函数，F6(x)～F8(x)为混合函数(hybrid functions)，F9(x)～F15(x)为构造函数(composition functions)。混合函数将函数变量分为多个子分量，每个子分量分别受到基本的单模函数或多模函数的影响，所以混合函数是否属于单模或多模函数取决于作用在子变量的基本函数。构造函数是由多个基本函数组合而成。函数的具体描述可参见文献[30]。

15个函数的搜索空间为[-100, 100]D，其中，D是空间的维数，x*表示函数的全局最佳位置，x*被设置为[-80, 80]D的随机数，有效避免优化算法受变量初值的影响。函数的最优值(最小值)被设置为函数序号×100，即F1(x*)=100，F2(x*)=200，…，F15(x*)=1 500。函数的维数设置为30。

3.2 实验环境设置

基于算法对应文献的推荐配置，实验所应用的算法的参数设置如表1所示，其中，Vmaxd表示粒子第d维速度的最大值，即粒子速度vkd限制在[-Vmaxd,Vmaxd]中；Range表示粒子位置各维的变化范围，由于函数搜索空间为[-100, 100]D，所以Range=200。为验证算法的有效性，EPSO不仅与基础算法GPSO[12]，LPSO[13]，BBPSO[23]和FIPS[15]进行比较，还与知名的CLPSO[24]进行比较。

表1 参数设置Tab.1 Parameter configurations

为反映环境的随机性对实验结果的影响，对于每个测试函数，实验运行51次[30]。各串行算法的粒子群中粒子数量为40，根据文献[30]，最大迭代次数MaxFES设置为40×104=4×105。本文的EPSO算法的参数设置为step=MaxFES/10=4×104，即各串行算法运行过程中进行10次信息共享；各串行算法的粒子群的粒子数量为40，算法的收敛条件是迭代次数达到MaxFES。由于各串行算法的计算复杂度不同，因此，EPSO需要等待最慢的串行算法达到MaxFES后才结束。

实验的计算机配置为CPU AMD 6核Fx-6300，内存8 GByte，固态硬盘120 GByte，计算机最大能开启6个工作单元。

3.3 实验结果分析

本文采用51次实验结果的均值和均方差作为统计指标。均值越接近于最优值，说明算法的准确度越高；若均方差越小，说明算法的稳定度越高。表2列出了6种算法在15个函数上寻优结果，其中，最小均值和最小均方差用#标明,表示6种算法测试值中的最好值。

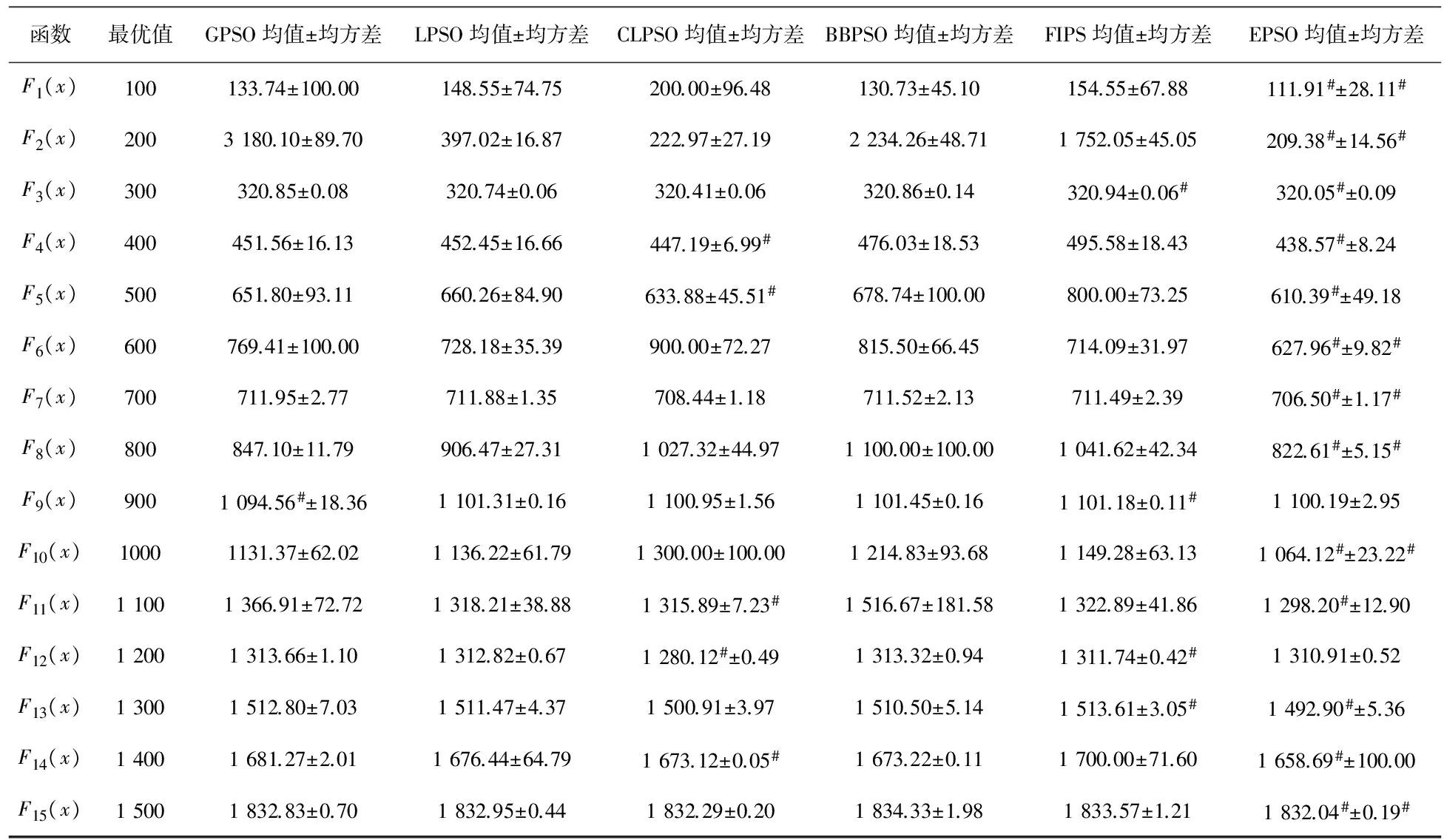
表2 统计结果比较Tab.2 Statistical results comparison

备注：每行最小均值和最小均方差用#标明。

从表2可知，GPSO和CLPSO分别在F9(x)和F12(x)上取得最优均值，而EPSO在剩余的13个函数上取得较好的均值。EPSO在7个函数上取得最优均方差，EPSO在其余函数上的均方差接近于6种算法的最优均方差。

表3列出了各算法的Friedman测试结果，EPSO排名第1，位列第2的是CLPSO，这表明EPSO的综合性能最好。虽然GPSO，LPSO，BBPSO和FIPS测试排名不如CLPSO，但这4种算法集成为EPSO后，性能优于CLPSO，显示集成策略的有效性。

表3 各对比算法的Friedman测试结果Tab.3 Friedman test results of the comparison algorithms

图3显示的是EPSO和其他5种算法在函数F2(x)，F3(x)，F7(x)，F12(x)上的收敛曲线。F2(x)，F3(x)，F7(x)，F12(x)的类型分别对应单峰函数、简单多模函数、混合函数、构造函数。从图3可知，EPSO的收敛速度是最快的，主要是由于EPSO在运算过程中结合了不同算法寻找的最优值。

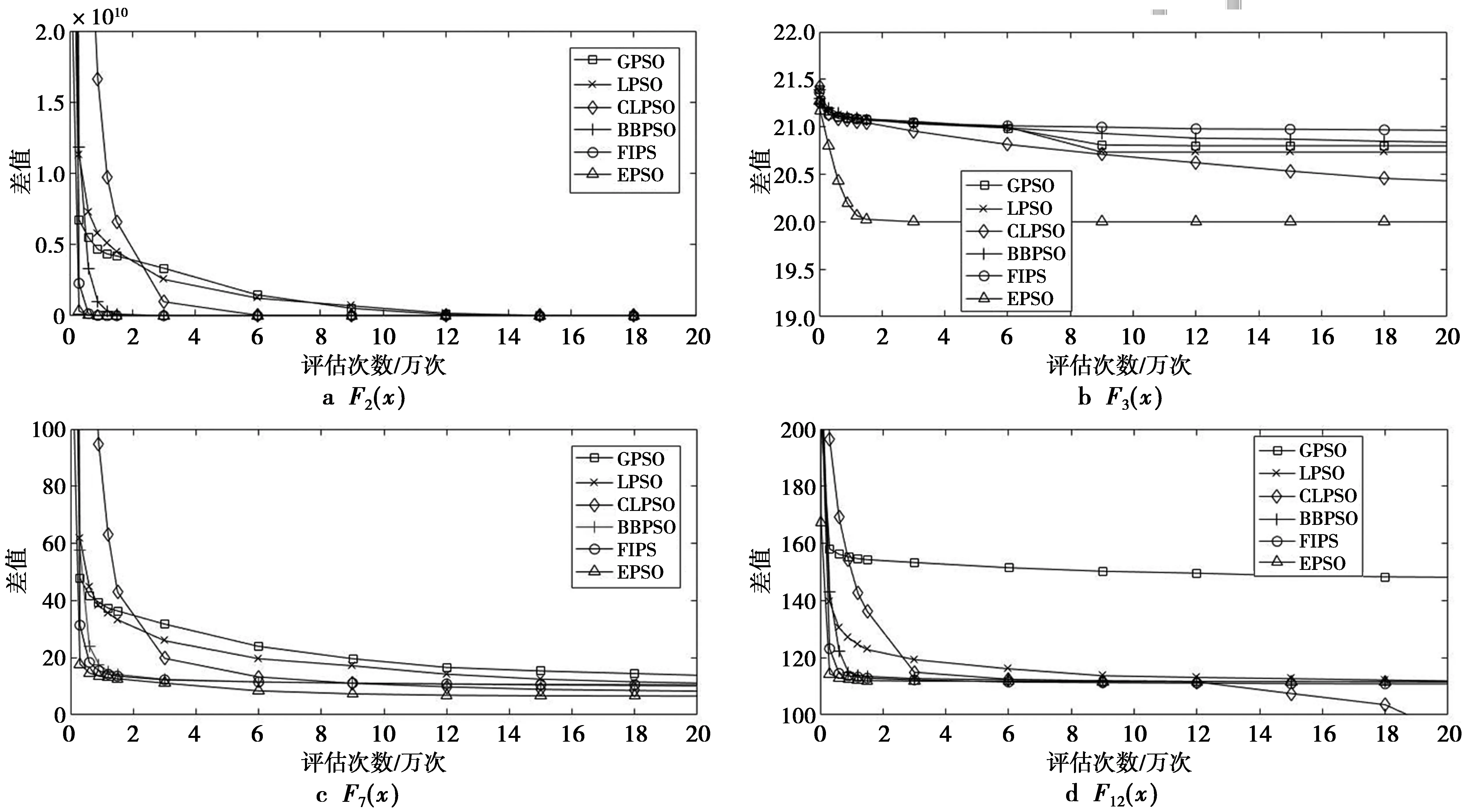
图3 6种算法在F2(x)，F3(x)，F7(x)，F12(x)上的收敛曲线Fig.3 Convergence curve of six algorithms on functions F2(x),F3(x),F7(x),F12(x)

6种算法的运行时间对比如表 4所示。从表4中可以看出，5种SPSO中GPSO的运行时间最短，主要原因是算法最简单；其次是LPSO，增加了邻域计算；而CLPSO和BBPSO运行时间相对较长，主要原因是CLPSO的学习策略较复杂，BBPSO的多元分布计算消耗较多时间；EPSO是6种算法中最长的，主要原因是除了基本的迭代运算，工作单元管理、任务分配、工作单元之间通信都会耗费时间。表4中的增量表示EPSO与5种SPSO的最大运行时间均值之差。结果显示，EPSO的运行时间增加量在[2,8]s，并不多，EPSO运行时间的均方差比其余几种算法稍大，但相差大约0.2s，说明算法比较稳定。

表4 运行时间比较Tab.4 Runtime comparisons

备注：每行最大的前2个均值用#标明，增量表示EPSO算法与5种串行PSO的最大均值之差。

由于BBPSO的多元分布计算比较复杂，其时间复杂度高于GPSO，LPSO，FIPS。EPSO的时间复杂度主要取决于BBPSO，从表4可以看出，EPSO的运行时间与BBPSO相当。

当每种算法选取的粒子数量是一样时，EPSO的空间需求量是GPSO，LPSO，FIPS，BBPSO的4倍多。当每个串行算法采用40个粒子，采用双精度浮点数存储每个粒子的速度、位置、个体最佳位置，EPSO用于存储粒子需要的空间为40×8 Byte×3×4=3 840 Byte，因为EPSO是并行的，需要额外的空间存储临时变量，所以实际的空间需求量会高于3 840 Byte。现在的计算机内存一般配置2 GByte以上，所以EPSO的空间需求量并不会给计算机带来压力。

实验结果表明，通过并行计算和信息共享，EPSO的测试准确度不仅优于集成的4种SPSO算法，还优于知名的CLPSO算法的最好测试结果，并且其标准差与5种SPSO的最小标准差比较接近。同时，EPSO运行时间增加并不多。

4 结 论

SPSO算法已在多个领域发挥重要的作用。提出的集成粒子群算法EPSO使用Matlab SPMD并行结构发挥单节点多核计算能力，实现4种SPSO算法的并行计算，充分发挥不同SPSO的优势，设置档案收集不同粒子群的最佳位置，通过粒子的随机替换，促进不同粒子群之间的信息共享。在广泛使用的测试集上进行仿真实验，实验结果表明，EPSO在保持较好的稳定度以及运行时间增加不多的前提下，准确度优于知名的SPSO算法。EPSO的算法框架是灵活的，可以进行扩展，通过集成多种各具特色的粒子群算法，使得粒子群算法能够适应更多场合。

[1] ZHANG J, ZHAN Z, LIN Y, et al. Evolutionary computation meets machine learning: A survey[J]. IEEE Computational Intelligence Magazine, 2011, 6(4): 68-75.

[2] KENNEDY J, EBERHART R. Particle swarm optimization[C]// IEEE Proceedings of the International Conference on Neural Networks. Piscataway: IEEE Press,1995: 1942-1948.

[3] DORIGO M, BIRATTARI M, STUTZLE T. Ant colony optimization[J].IEEE Computational Intelligence Magazine, 2006, 1(4): 28-39.

[4] KARABOGA D, GORKEMLI B, OZTURK C, et al. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications[J].Artificial Intelligence Review, 2014, 42(1): 21-57.

[5] YANG X. Firefly algorithms for multimodal optimization[M].Watanabe O, Zeugmann T：Springer Berlin Heidelberg,2009, 169-178.

[6] ZHANG Y, WANG S, JI G.A comprehensive survey on particle swarm optimization algorithm and its applications[EB/OL].(2015-02-12)[2016-06-01].http://www.hindawi.com/journals/mpe/aa/931256/.

[7] 侯燕, 郭慧玲. 关联规则挖掘结合简化粒子群优化的哈希回溯追踪协议[J].重庆邮电大学学报：自然科学版，2016, 28(02): 239-246. HOU Yan,GUO Huiling. Hash IP trace-back protocol based on association rule mining and simplified particle swarm optimization[J].Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition, 2016, 28(02): 239-246.

[8] 孙延维, 彭智明, 李健波. 基于粒子群优化与模糊聚类的社区发现算法[J].重庆邮电大学学报：自然科学版，2015, 27(05): 660-666. SUN Yanwei, PENG Zhiming, LI Jianbo. Community detection algorithm based on particle swarm optimization and fuzzy clustering[J].Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition, 2015, 27(05): 660-666.

[9] WAINTRAUB M, SCHIRRU R, PEREIRA C M N A. Multiprocessor modeling of parallel Particle Swarm Optimization applied to nuclear engineering problems[J]. Progress in Nuclear Energy, 2009, 51(6-7): 680-688.

[10] MUSSI L, DAOLIO F, CAGNONI S. Evaluation of parallel particle swarm optimization algorithms within the CUDA? architecture[J]. Information Sciences, 2011, 181(20): 4642-4657.

[11] TU K,LIANG Z.Parallel computation models of particle swarm optimization implemented by multiple threads[J].Expert Systems with Applications,2011,38(5):5858-5866.

[12] SHI Y, EBERHART R. A modified particle swarm optimizer[C]//IEEE.Proceedings of the IEEE Congress on Evolutionary Computation.Piscataway:IEEE Press，1998:69-73.

[13] KENNEDY J, MENDES R. Population structure and particle swarm performance[C]//IEEE.Proceedings of the IEEE Congress on Evolutionary Computation.Piscataway: IEEE Press, 2002: 1671-1676.

[14] MENDES R, KENNEDY J, NEVES J. The fully informed particle swarm: Simpler, maybe better[J].IEEE Transactions on Evolutionary Computation,2004,8(3): 204-210.

[15] KENNEDY J, MENDES R. Neighborhood topologies in fully informed and best-of-neighborhood particle swarms[J]. IEEE Transactions on Systems Man and Cybernetics Part C Applications and Reviews,2006,36(4):515-519.

[16] 占栋辉, 卢厚清, 郝文宁, 等. 一种高斯反向学习粒子群优化算法[J].小型微型计算机系统， 2015, 36(5): 1064-1068. ZHAN Donghui, LU Houqing, HAO Wenning, et al.Particle Swarm Optimization Algorithm with Gaussian Opposition-based Learning[J].Journal of Chinese Computer Systems,2015,36(5):1064-1068.

[17] 赵嘉, 付平, 李崇侠, 等. 基于不同学习模型的精英反向粒子群优化算法[J].小型微型计算机系统，2015,36(6): 1368-1372. ZHAO Jia, FU Ping, LI Chongxia, et al. Particle Swarm Optimization Based on Elite Opposition Learning Using Different Learning Models[J].Journal of Chinese Computer Systems, 2015,36(6): 1368-1372.

[18] 戴月明, 朱达祥, 吴定会. 核矩阵协同进化的震荡搜索粒子群优化算法[J].重庆邮电大学学报：自然科学版，2016, 28(02): 247-253. DAI Yueming,ZHU Daxiang,WU Dinghui.Shock search particle swarm optimization algorithm based on kernel matrix synergistic evolution[J].Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition, 2016, 28(02): 247-253.

[19] CLERC M, KENNEDY J.The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J].IEEE Transactions on Evolutionary Computation,2002,6(1): 58-73.

[20] 许君, 鲁海燕, 石桂娟. 限制速度粒子群优化和自适应速度粒子群优化在无约束优化问题中的应用[J].计算机应用，2015, 35(3): 668-674. XU Jun,LU Haiyan,SHI Guijuan.Application of restricted velocity particle swarm optimization and self-adaptive velocity particle swarm optimization to unconstrained optimization problem[J].Journal of Computer Applications, 2015, 35(3): 668-674.

[21] 陈寿文. 基于质心和自适应指数惯性权重改进的粒子群算法[J]. 计算机应用，2015, 35(3): 675-679. CHEN Shouwen.Improved particle swarm optimization algorithm based on centroid and self-adaptive exponential inertia weight[J].Journal of Computer Applications, 2015, 35(3): 675-679.

[22] 奚茂龙,盛歆漪,孙俊.基于多维问题的交叉算子量子粒子群优化算法[J].计算机应用，2015,35(3):680-684. XI Maolong,SHENG Xinyi,SUN Jun. Quantum-behaved particle swarm optimization algorithm with crossover operator to multi-dimension problems[J]. Journal of Computer Applications, 2015, 35(3): 680-684.

[23] KENNEDY J. Bare bones particle swarms[C]//IEEE.Proceedings of the IEEE Swarm Intelligence Symposium. Piscataway: IEEE Press, 2003: 80-87.

[24] LIANG J J, QIN A K, SUGANTHAN P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(3): 281-295.

[25] CAMPOS M, KROHLING R A, ENRIQUEZ I. Bare bones particle swarm optimization with scale matrix adaptation[J]. IEEE Transactions on Cybernetics, 2014, 44(9): 1567-1578.

[26] MathWorks, Inc. Parallel computing toolbox[EB/OL]. (2015-09-01)[2016-06-01].http://cn.mathworks.com/help/distcomp/.

[27] GOH C K, TAN K C, LIU D S, et al. A competitive and cooperative co-evolutionary approach to multi-objective particle swarm optimization algorithm design[J]. European Journal of Operational Research,2010,202(1):42-54.

[28] ZHANG G, ZHAN Z, DU K, et al. Parallel particle swarm optimization using message passing interface[C]//Proceedings of the 18th Asia Pacific Symposium on Intelligent and Evolutionary Systems.Cham, Switzerland:Springer International Publishing, 2015: 55-64.

[29] ALBA E, TOMASSINI M. Parallelism and evolutionary algorithms[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(5): 443-462.

[30] LIANG J J, QU B Y, SUGANTHAN P N, et al. Problem Definitions and Evaluation Criteria for the CEC 2015 Competition on Learning-based Real-Parameter Single Objective Optimization[R].Zhengzhou, China: Computational Intelligence Laboratory, 2014.

(编辑：王敏琦)

s：The National Science Fund for Young Scholars of China(61301232, 61501174); The Key Scientific Research projects of Higher Education of Henan Province of China(17A520026); The Doctoral Program of Henan Institute of Engineering(D2012016)

Serial particle swarm optimizer (SPSO) is popularly applied in many areas. SPSO variants are proposed to solve different kinds of optimization problems，but there are differences between the performances. Therefore, an ensemble particle swarm optimizer (EPSO) was proposed to improve SPSO’s ability to adapt to problems. The parallel structure single program multiple data (SPMD) in Matlab was utilized to play single node multicore computing power. An outside archive was set to share the global best positions of different particle swarms and further facilitate information exchange of different SPSOs. SPSOs’ advantages to solve different kinds of optimization problems were synthesized by the new algorithm. Simulation experiments conducted on a set of widely used benchmark functions verify the effectiveness of the new algorithm. Compared with several well-known SPSO variants, the new algorithm has a significant advantage in optimizing performance. The new algorithm can not only improve the adaptability of PSO, but also adapt to the other swarm intelligent algorithms to improve the algorithm performance.

single program multiple data; ensemble particle swarm optimizer; global numerical optimization; particle swarm optimizer; parallel computing

10.3979/j.issn.1673-825X.2017.04.016

2016-10-07

2017-02-26 通讯作者：何 莉 engineerheli@126.com

国家自然科学基金青年项目(61301232，61501174)；河南省高等学校重点科研项目(17A520026)；河南工程学院博士基金(D2012016)

TP393

A

1673-825X(2017)04-0527-08

Ensemble particle swarm optimizer for single objective optimization

(School of Computer, Henan Institute of Engineering, Zhengzhou 451191, P. R. China)

何 莉(1982-)，男，江西萍乡人，讲师，博士，研究方向为智能计算、物联网。E-mail：engineerheli@126.com。 王 淼(1981-)，男，河南南阳人，副教授，博士，研究方向为空间关系数据库。E-mail：506872858@qq.com。 李 博(1982-)，男，河南许昌人，讲师，博士，研究方向为群智能和图像处理。E-mail：422873809@qq.com。

HE Li, WANG Miao, LI Bo