基于模糊ART划分的目标分群算法
樊振华,师本慧,陈金勇,段同乐,王长力
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081; 2.中国人民解放军91635部队,北京 102249)
基于模糊ART划分的目标分群算法
樊振华1,师本慧1,陈金勇1,段同乐1,王长力2
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081; 2.中国人民解放军91635部队,北京 102249)
针对目标分群中存在的分类数未知和噪声干扰问题,提出一种基于模糊ART划分的目标分群算法。通过目标识别属性划分,约减分群目标数规模,降低计算量;通过划分数据预处理消除尺度差异,在此基础上采用基于模糊ART的目标空间划分,经类选择、匹配度检验和类学习等步骤实现对目标的增量式动态分群。试验结果表明,该算法对复杂环境下未知分类数的多目标编队分群具有良好的有效性、稳健性和实时性。
目标分群;空间划分;模糊ART;属性划分
0 引言
态势显示是指挥员对实时情况把控的有效信息获取途径,为制定方案与决策提供基础和支撑[1]。通常,目标在执行任务的过程中是以编队的形式完成巡航、撤退等具体行动。如果仍将每个目标看作孤立的个体,显然存在信息冗余,而且密布的目标标识还会造成信息炫目问题,使指挥员无法快速直接地了解态势概况,做出高效的指挥决策[2]。因此,需要将识别属性和运动参数等特征相近的目标聚合归类,划分为若干个群目标,与其实际执行任务的编队相对应[3]。这样,一方面可以简化态势显示,利于指挥员迅速掌控全局[4];另一方面,目标分群后的结果能够更为直接地体现其任务编队的本质,从海量信息中挖掘出行动意图,为后续的态势分析奠定基础。
目标分群[5]实质上是一个数据聚类问题,将特征空间中分布相近的目标聚合为一类。按照分类数是否需要预先设定,聚类方法通常可以分为:类数已知算法和类数未知算法。其中,类数已知算法中典型的方法有模糊C均值算法[6]和K均值算法[7]。该类算法存在的缺陷[8]:一方面,需要预设分类数与通常面临分类数未知的情况不匹配[9];另一方面,其分类结果对初始分类中心选取的依赖性较强,进而造成分类结果稳定性欠佳[10]。类数未知算法[11]中典型的方法有最近邻算法[12]和ISODATA算法[13]。最近邻算法通过设定阈值实现分群,简单易实现且应用广泛,但缺乏有效的阈值选取方法[14],难以有效处理不同量测尺度或情况的分群问题。ISODATA算法通过对聚类结果的合并和分裂操作实现类数未知情况下的动态分群,但其以样本与聚类中心的距离作为分群依据,适合于解决球状簇样本分群问题,而对于常见的线型编队分群问题存在不足[15]。
针对上述问题,本文首先通过目标识别属性划分,约减参与分群目标数的规模,从而提高计算效率;其次通过划分数据预处理消除尺度差异,采用基于模糊ART[16]的目标空间划分,经类选择、匹配度检验和类学习等步骤实现对目标的增量式动态划分,能够在噪声干扰下有效处理分类数未知的多编队分群问题。
1 目标识别属性划分
目标分群主要是针对目标位置量测和识别属性进行划分。由于位置量测连续无限性和识别属性的离散有限性,二者的划分计算复杂度差异较大。其中,目标识别属性划分计算复杂度低,而目标空间划分的计算复杂度则较高。因此,本文拟先进行目标识别属性划分,后进行目标空间划分。这样可以将目标集整体的空间划分问题分解为多个目标子集的空间划分问题,有效约减参与空间划分的目标数规模,从而降低计算量。


i=1,2,j=1,2,…,C。
(1)
式中,i为红/蓝方标号;j为类别标号;C为类别总数。在此基础上,分别对每个红/蓝方各类目标集Pij进行空间划分。
2 基于模糊ART的目标空间划分
自适应谐振理论(AdaptiveResonanceTheory,ART)[16]通过模拟人类认知信息的处理过程,构建实时神经网络,从而实现无监督的分类学习和模式认知。ART衍生出一系列实时神经网络模型,其中具有代表性的模糊ART就是通过引入模糊集理论所形成的实时神经网络模型[17]。模糊ART划分算法流程,如图1所示。

图1 模糊ART划分算法流程
2.1 划分数据预处理
由于待划分数据的尺度及L1范数存在差异,为了保证后续处理的一致性和类学习的稳定性,需要对待划分数据进行量测归一化和补充编码。
其次,对L′进行补充编码,得到输入向量

(2)

2.2 类选择
每个类对应一个权重向量wj=(wj1,wj2,…,wjd),j=1,2,…,N,N为当前类数,d为分类特征为数,此处d=4。wj为所有属于该类样本的最大模糊子集,是这些样本所具有的共性的体现,因此用wj来表征该类。对于输入向量I和权重向量wj,定义类选择函数
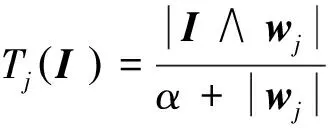
(3)

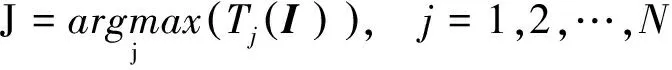
(4)
2.3 匹配度检验
计算输入向量I和权重向量wJ的匹配度函数

(5)

2.4 类学习
为了保证权重向量能够有效反应所属类的所有样本的共性,需要通过类学习,将新划入该类的样本融合到权重向量当中,
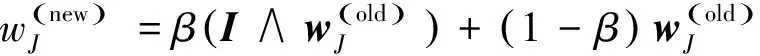
(6)

3 仿真实验与分析
本文实验环境为IntelCorei3-2130 3.4GHzCPU,2GB内存,Windows7操作系统,MatlabR2011a仿真实验平台。首先,比较和分析模糊ART划分、模糊C均值[18]、K均值[7]和ISODATA[13]这4种算法在近距离场景下对典型多编队群目标进行空间分群的性能;其次,将基于模糊ART的目标空间划分与目标识别属性划分结合,并应用于动态目标分群当中,从而进一步验证其在过程噪声和观测噪声叠加干扰下的适用性和稳定性。
3.1 近距离多编队空间分群实验
目标空间分群实验结果如图2所示。在图2中有2组目标编队,分别呈三角形(左侧)和线形(右侧)。由图2可以看出,模糊ART划分、模糊C均值和K均值均可得到较为理想的空间分群结果。然而,模糊C均值和K均值的分类数均需预设为真实值2,且分类数预设值直接影响分类结果的正确性,当分类数设定错误时必然得到错误的分群结果,因而难以满足实际中分类数未知情况的分群需求;而模糊ART划分则无需预设分类数,且能够得到正确的分群结果;ISODATA算法虽然也无需预设分类数,但其以样本与聚类中心的距离作为分群依据,不适合解决线型编队的分群问题,尤其当线型编队内目标最大间距与编队间最小距离接近时,该算法的参数设置尤为困难,难以获得理想的分群结果。

图2 多编队空间分群结果比较
在此基础上,对上述分群场景进行1 000次运行,统计平均得到各种算法的运行时间,如表1所示。可以看出,后3种算法均需要通过迭代计算实现分群,较为耗时;而模糊ART划分结合自适应谐振理论与模糊集理论,可以实现增量式动态分群,直接得到分群结果,运行效率更高。

表1 目标空间分群算法运行时间比较
综上所述,本文提出的基于模糊ART划分的目标空间分群算法能够有效并快速处理分类数未知的多编队空间分群问题,即使在编队间距较小的复杂场景下,仍然可以获得较好的分群结果。
3.2 动态目标分群实验
对静态的近距离多编队空间分群进行了讨论和分析,然而实际应用中的目标分群还需要进行目标识别属性划分,是一个更为复杂的连续动态目标分群问题。其中,考虑到目标受地形、气流、自身操控和观测误差等影响,存在过程噪声与观测噪声,这使得观测到的编队内目标间距也持续动态变化,给准确分群增加了难度。
多编队群目标运动轨迹如图3所示,虚线矩形框为便于观察实验结果的局部区域,局部区域旁边的字母A和字母B为局部区域所对应的编号,黑色六角形为各群目标观测起始位置,各群目标编队情况如表2所示。仿真场景中,目标运动的过程噪声标准差为1 000 m,观测噪声标准差为50 m。图3所描绘的态势情况为蓝方飞机与车辆多编队向红方车辆编队快速行进,遭遇红方飞机编队拦截后撤退。针对上述场景,将目标识别属性划分与基于模糊ART的目标空间划分结合,实现目标分群,结果如图3、图4和图5所示。

图3 多编队群目标运动轨迹及全局分群结果
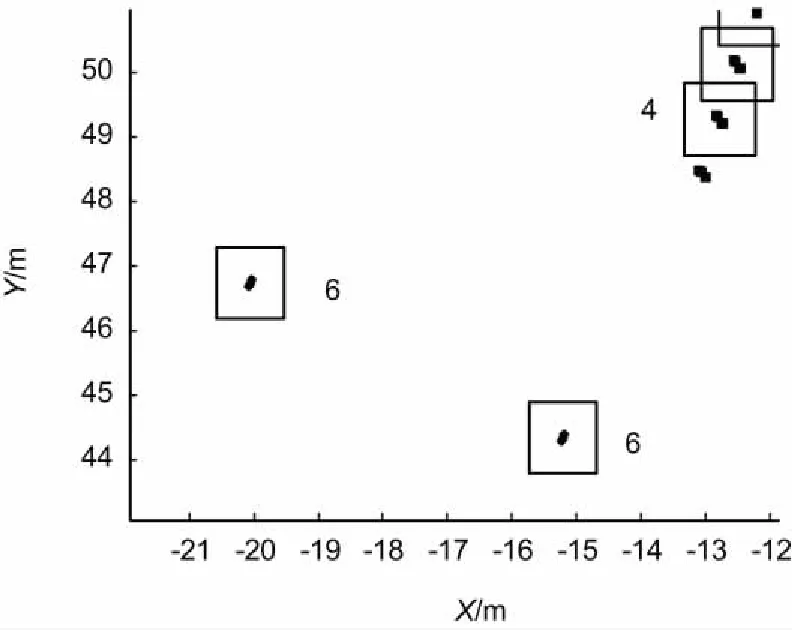
图4 局部区域A目标分群结果

图5 局部区域B目标分群结果
图4和图5为局部放大结果。图3、图4和图5中,黑点表示各目标的位置量测,实线矩形框范围内的多个目标被划分属于同一群目标,各群目标运动轨迹旁边的数字为群目标所对应的编号。可以看出,虽然受噪声的影响,观测得到的编队内目标间距持续变化,但是本文算法能够实现增量式高效的动态分群,有效处理分类数未知的多编队分群问题。
在此基础上,对上述分群场景进行1 000次运行,统计平均得到本文算法的运行时间为0.003 9 s。本文算法一方面通过目标识别属性划分,将29个目标的分群问题拆分成目标数分别为7、8、8和6的4个目标子集的分群问题,有效约减了参与空间划分的目标数规模;另一方面,通过模糊ART划分实现增量式的目标分群,也有效提高了算法运行效率。

表2 各群目标编队情况
4 结束语
针对态势显示的精炼简化需求,本文提出一种基于模糊ART划分的目标分群算法,并通过仿真实验检验了所提算法的性能。一方面,验证了所提算法在近距离场景下对典型多编队群目标进行空间分群的性能明显优于传统算法(模糊C均值、K均值和ISODATA);另一方面,验证了所提算法对于复杂环境动态多编队目标分群,能够实现增量式的高效处理,有效解决了目标分群中存在的分类数未知和噪声干扰问题。
目标分群结果能够有效地体现其任务编队的本质,不仅简化了态势显示,而且为后续的威胁估计与意图分析提供了技术支撑。更高层次的态势分析需要以此为基础,做更深入的研究。
[1] 田聚波.面向图形作业的协同指挥系统设计与实现[J].无线电通信技术,2016,42(2):92-95.
[2] 洪旭,柳虔林,丁洪伟,等.应急机动指挥通信能力评估分析[J].无线电通信技术,2015,41(4):20-23.
[3] 段同乐,张冬宁.二叉树多分类SVM在目标分群中的应用[J].无线电工程,2015,45(6):88-91.
[4] 梁健,陈晧晖.基于全分布式处理的统一态势生成技术研究[J].无线电工程,2016,46(1):12-15.
[5] 艾伟,张冬宁.一种基于分群矩阵的目标动态分群算法[J].无线电工程,2015,45(11):64-68.
[6] CANNON R L,DAVE J V,BEZDEK J C.Efficient Implementation of the Fuzzy C-means Clustering Algorithms[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1986(2):248-255.
[7] KANUNGO T,MOUNT D M,NETANYAHU N S,et al.An Efficient K-means Clustering Algorithm:Analysis and Implementation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(7):881-892.
[8] 肖满生,肖哲,文志强,等.模糊C均值聚类区间型模糊化参数模型[J].系统工程与电子技术,2015,37(4):868-873.
[9] CARVALHO M J,MELO-GONÇALVES P,TEIXEIRA J C,et al.Regionalization of Europe Based on a K-means Cluster Analysis of the Climate Change of Temperatures and Precipitation[J].Physics and Chemistry of the Earth,Parts A/B/C,2016,94(8):22-28.
[10] KUNCHEVA L I,VETROV D P.Evaluation of Stability of K-means Cluster Ensembles with Respect to Random Initialization[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(11):1 798-1 808.
[11] 张琨,王翠荣.一种自适应分裂与合并的运动目标聚类分割算法[J].电子与信息学报,2014,36(3):601-609.
[12] ERTOZ L,STEINBACH M,KUMAR V.A New Shared Nearest Neighbor Clustering Algorithm and Its Applications[C]∥ Workshop on Clustering High Dimensional Data and Its Applications at 2nd SIAM International Conference on Data Mining,2002:105-115.
[13] MEMARSADEGHI N,MOUNT D M,NETANYAHU N S,et al.A Fast Implementation of the ISODATA Clustering Algorithm[J].International Journal of Computational Geometry & Applications,2007,17(1):71-103.
[14] BEYER K,GOLDSTEIN J,RAMAKRISHNAN R,et al.When is “Nearest Neighbor” Meaningful?[C]∥ International Conference on Database Theory,1999:217-235.
[15] 王晓璇.陆战场装甲目标聚合算法研究[D].南京:南京理工大学,2007.
[16] CARPENTER G A,GROSSBERG S,ROSEN D B.Fuzzy ART:Fast Stable Learning and Categorization of Analog Patterns By an Adaptive Resonance System[J].Neural Networks,1991,4(6):759-771.
[18] BEZDEK J C,EHRLICH R,FULL W.FCM:The Fuzzy C-means Clustering Algorithm[J].Computers & Geosciences,1984,10(2-3):191-203.
A Fuzzy ART Based Target Clustering Algorithm
FAN Zhen-hua1,SHI Ben-hui1,CHEN Jin-yong1,DUAN Tong-le1,WANG Chang-li2
(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China; 2.Unit91635,PLA,Beijing102249,China)
Target clustering is confronted with problems of unknown category number and noise interference.To solve these problems,a fuzzy ART based target clustering algorithm is proposed.In this algorithm,the clustering target number is reduced through attribute partition to lessen the computational burden.Through data preprocessing,the scale difference is eliminated.On this basis,target space partition based on fuzzy ART is adopted,incremental dynamic clustering of targets is achieved through category choice,resonance and learning.Experimental results show the effectiveness,stability and real-time performance of the proposed algorithm in multi-formation clustering with unknown category number in complicated environment.
target clustering;space partition;fuzzy adaptive resonance theory;attribute partition
10.3969/j.issn.1003-3106.2017.09.06
樊振华,师本慧,陈金勇,等.基于模糊ART划分的目标分群算法[J].无线电工程,2017,47(9):27-31.[FAN Zhenhua,SHI Benhui,CHEN Jinyong,et al.A Fuzzy ART Based Target Clustering Algorithm[J].Radio Engineering,2017,47(9):27-31.]
TP391
A
1003-3106(2017)09-0027-05
2016-11-16
海洋公益性科研专项基金资助项目(201505002)。
樊振华 男,(1985—),博士,工程师。主要研究方向:态势估计、目标分群、计算机视觉。
师本慧 男,(1965—),研究员。主要研究方向:指挥控制、态势估计、航天地面应用和测控。

