基于细线距离顺序统计量指静脉快速识别算法
李小刚,沈 雷,张严严,蓝师伟
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
基于细线距离顺序统计量指静脉快速识别算法
李小刚,沈 雷,张严严,蓝师伟
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
为了提高低质量手指静脉图像的识别率,提出了一种基于细线距离顺序统计量的手指静脉快速识别算法.利用顺序统计量计算部分较小细线距离的平均值,提高了存在伪静脉手指图像识别性能.在细线点集距离计算中采用邻域搜索的方法,相比采用逐点匹配的MHD点集计算方法,缩短了大量的匹配时间.实验结果表明,所提算法比广泛使用的基于特征点的MHD算法具有更好的性能.
手指静脉;匹配识别;MHD算法
0 引 言
手指静脉识别技术是依据手指内固有的静脉特征来识别个体,静脉纹路具有不可复制的、唯一的活体特征.近年来手指静脉识别技术得到了迅速的发展,具有广阔的应用领域.
Miura N.等[1]提出了一种基于模板匹配的静脉识别方法,将采集到的静脉图像应用嵌入式隐马尔科夫模型来识别手指.该方法操作的复杂度较高,识别时间较长.王科俊等[2]采用一种融合小波矩和主成分分析的方法来识别静脉.该方法识别性能较好,但需要将图像矩阵转化为一维向量,当图像矩阵较大时,主分量分析计算量较大.双向二维主成分分析[3]和二维费希尔主成分分析[4]等基于全局特性的方法,将手指静脉图像变换到最佳投影空间产生新的特征,很好地保留了图像的纹路、形状等全局特性,但因为最佳投影空间是通过训练样本确定的,系统鲁棒性受到训练样本的影响[5].
因Hausdorff距离[6](Hausdorff Distance,HD)相比于其他的识别方法,计算方便且不需要建立点之间的一一对应关系,只是计算两个点集之间的相似程度(最大距离),因此HD被广泛研究并应用于手指静脉识别领域.图像质量较低时,基于特征点HD识别方法对引起的静脉特征点位置微小扰动非常敏感,为了克服该缺点,文献[7]在原始的Hausdorff距离算法上进行了修改,提出了基于特征点平均距离值的Hausdorff距离方法(modified Hausdorff distance,MHD).利用MHD匹配手指静脉具有良好的识别性能,但提取出的静脉的特征点只是静脉细线的一部分,特征点丢失了大量的静脉信息,不能表征整个静脉图像,特别是对于静脉稀疏、静脉纹路不明显的低质量手指图像,MHD算法识别性能显著下降.
针对以上问题,本文提出了一种基于细线距离顺序统计量的手指静脉快速识别算法,算法利用同根手指相似程度更高的静脉纹路作为匹配对象,采用顺序统计量计算部分较小细线距离的平均值,有效的提高了手指静脉的识别性能;在细线点集距离计算中提出了邻域搜索匹配的方法,节省了大量的运算时间.
1 静脉细化与特征点提取
用采集器采集原始手指静脉图像,然后对得到的原始静脉图像进行滤波,尺寸灰度归一化,再用方向滤波器对图像进行分割细化,得到手指静脉的细化拓扑结构,静脉相交的地方形成了交叉点,在两端被截断的地方形成端点,交叉点与端点组成了手指静脉的特征点.
同根手指静脉低质量图像细化和特征点如图1所示.可以看出,图1(a)两幅同根手指静脉的低质量细化图相似程度要高于图1(b)两幅同根手指静脉的低质量特征点的相似程度,图1(b)很难看出是来自同一根手指的特征点,因此若利用静脉细化纹路匹配识别会有更高的识别率.图1(a)的质量较差,两幅图中都存在少量的伪静脉,为了减小伪静脉对匹配的影响,利用顺序统计量来计算部分较小细线距离的平均值.

图1 低质量手指静脉图像细化和特征点图
2 MHD算法
2.1 传统的Hausdorff算法
给定2个有限点集合A={a1,a2,…,ap}和B={b1,b2,…,bp},则A,B之间的Hausdorff距离定义为

(1)
其中

(2)
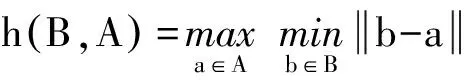
(3)
函数h(A,B)和h(B,A)分别称为前向和后向HD.h(A,B)的值取决于集合A所有点中离B最远的那个点.若h(A,B)=d,则表示A中所有点到B中点的距离不超过d,即A中所有点到B的距离都在d的范围之内.
2.2MHD算法
为了降低特征点扰动对HD算法的影响,文献[7]在原始Hausdorff距离公式的基础上提出了MHD公式,定义为:
(4)
MHD与HD的区别在于:h(A,B)取决于点集A中的所有点到点集B的距离的平均.
3 基于细线距离顺序统计量的快速识别算法
3.1 基于细线距离顺序统计量的识别算法
将MHD算法直接应用于对静脉细线的匹配识别,性能易受伪静脉的影响.若点集A和点集B是同根手指静脉图像的细线点集合,点集A和点集B很相似,但是点集B中在细化的过程中出现了少数的伪静脉,此时,若采用MHD算法计算这2个点集之间的距离,算出的MHD值就会很大.在低质量手指图像识别时,为了减小伪静脉对距离值的影响,本文提出了基于细线距离顺序统计量的识别方法.利用细线距离顺序统计量得到细线点集距离较小值的平均值,从而减小了伪静脉对识别性能的影响.其基本原理如下:同根手指的静脉纹路走势是一致的,只有对伪静脉匹配时才会出现较大的距离值,利用顺序统计量求得部分较小细线点集距离平均值,有效地减小了伪静脉对结果的影响.不同手指静脉纹路走势互不相同,利用顺序统计量求细线点集较小距离平均值并不能大幅度降低距离值.因此基于细线距离顺序统计量的方法降低了同类手指之间的差异性,提升了静脉的识别性能.
细线点集A到B的距离定义为:将细线点集A中p个点到细线点集B的距离值按升序排序,取前k个距离值的平均值作为点集A到点集B的距离值.
(5)
其中,1≤k≤p,p为点集A中点的个数,th表示升序排序.
同理,细线点集B到A的距离定义为:将点集B中q个点到点集A的距离值按升序排序,取前l个距离值的平均值作为点集B到点集A的距离值.
(6)
其中,1≤l≤q,q为点集B中点的个数,th表示升序排序.
点集A和点集B之间的距离定义为:
(7)
3.2 基于邻域搜索细线距离快速识别算法
静脉细化图的点数要远远多与静脉特征点数,如果利用逐点搜索的方法对静脉细线点进行匹配识别需要耗费大量的运算时间.本文提出了一种基于邻域搜索细线距离快速识别算法.

4 实验与结果分析
为了得到实验的图像数据库,在实验内采集静脉图像建立静脉图像库,共70组,每组8幅图像样本,一共560幅样本图像,在MATLAB平台上进行1∶1识别验证,图像大小为300×140像素,提取感兴趣区域并归一化后的图像大小为160×64像素,邻域搜索范围取3,式(5)中k取0.75×p,式(6)中l取0.75×q.在1∶1识别验证模式下,将每组中的1个样本分别和其他7个样本进行比对,称为合法匹配;将1组中手指静脉样本和其他手指中的样本进行比对,称为非法匹配.
分别采用文献[7]的MHD算法和本文方法对静脉特征点进行合法匹配和非法匹配,分布情况如图2所示.通过对比可以看出,采用本文算法对静脉细化点进行匹配识别时,其合法匹配与非法匹配之间的值交叉较少;合法匹配的值相对集中;且合法匹配与非法匹配的主峰相隔较远.所以本文提出的基于细线顺序统计量的手指静脉快速识别算法能够更有效地识别同类手指和区分不同类手指.
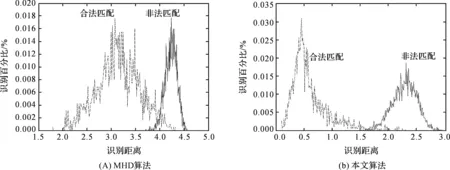
图2 合法与非法匹配距离值分布对比图
分别采用MHD算法对静脉特征点识别和本文算法对静脉细线点识别,得到拒识率(False Reject Rate,FRR)和误识率(False Accept Rate,FAR)关系曲线,即ROC曲线,如图3所示.从图3中可以看出,本文提出的基于细线顺序统计量的识别算法明显优于广泛使用的基于特征点的MHD算法.
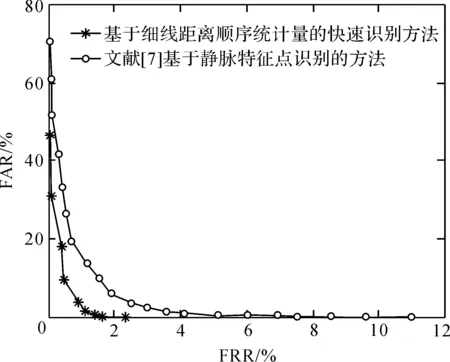
图3 ROC曲线比较
为了验证本文算法运算时间可行性,利用静脉图像库中70组560幅图像,在windows 10操作系统下(Intel i5-4590处理器,4GB运行内存)基于MATLAB7.10版本进行仿真.分别对560幅图像的特征点图、细线图统计得出,平均每幅静脉图像有45个特征点,706个细线点;利用本文提出的基于顺序统计量的邻域搜索方法,当邻域搜索范围取3时,对70组图像进行同类匹配,统计得出在(x±3,y±3)的范围内平均可以搜索到3.97个点.
由上述得出的实验数据可以分析得出3种静脉识别的平均匹配次数.3种静脉识别方法是文献[7]提出的MHD算法对特征点识别、MHD算法对细线点识别、本文提出的顺序统计量的邻域搜索方法对细线点识别,仿真结果如表1所示.从表1中可以看出,文献[7]提出的MHD算法匹配两幅静脉特征点图像平均需要进行45×45×2次比对;MHD算法匹配两幅静脉细线图像平均需要进行706×706×2次比对;本文提出的顺序统计量的邻域搜索方法匹配两幅静脉细线图像,平均需要进行706×3.97×2次比对.
完成1组8幅图像组内合法匹配需要进行28次匹配,70组图像完成组内合法匹配需要进行1 960次匹配.采用文献[7]提出的MHD算法完成70组静脉特征点图像组内匹配需要20.732 6 s,平均完成一次匹配的时间为0.010 6 s;采用文献[7]提出的MHD算法完成70组静脉细线图像组内匹配需要4 946 s,平均完成一次匹配的时间为2.523 5 s;本文提出的顺序统计量的邻域搜索方法完成70组静脉细线图像组内匹配需要70.560 4 s,平均完成一组匹配的时间为0.036 0 s.
3种静脉识别方法的平均匹配次数和平均匹配时间的结果分析得出,本文提出的基于细线距离顺序统计量的手指静脉快速识别算法,匹配两幅细线点图像需要匹配的次数(5 605次)接近于MHD算法对两幅特征点图像需要的匹配次数(4 050次),完成的时间0.036 0 s接近MHD算法完成的时间0.010 6 s,而相比于MHD算法对细线点匹配识别2.523 5 s,该算法大大降低了运算时间.

表1 3种静脉识别方法的仿真结果
5 结束语
本文提出了利用手指静脉细线纹路作为匹配对象的思想.利用顺序统计量计算细线点集部分较小距离求平均值的方法减小了伪静脉对静脉识别的影响,邻域搜索的匹配方法降低了两个静脉细化图点集之间的匹配时间.在计算两个静脉细化点集之间的距离值时,邻域搜索范围的大小受到了人工选取的制约,具有一定的局限性,需要进一步改进,实现邻域搜索范围的自适应选取.
[1]MIURA N, NAGASAKA A, MIYATAKE T. Feature Extraction of Finger-vein Patterns Based on Repeated Line Tracking and its Application to Personal Identification[J]. Machine Vision and Applications, 2004,15(4):194-203.
[2]王科俊,袁智.基于小波矩融合PCA变换的手指静脉识别[J].模式识别与人工智能,2007,20(5):692-697.
[3]管凤旭,王科俊,刘靖宇,等.归一双向加权(2D)2PCA的手指静脉识别方法[J].模式识别与人工智能,2011,24(3):417-424.
[4]YU C, QING H, ZHANG L. (2D)2 FPCA: An Efficient Approach for Appearance Based Object Recognition[C]//2009 3rd International Conference on Bioinformatics and Biomedical Engineering. 2009:1-4.
[5]杨颖,尹义龙,杨公平,等.融合局部特征和全局特征的手指静脉识别方法[J].计算机工程与应用,2012,48(14):158-162.
[6]HUTTENLOCHER D P, KLANDERMAN G A, RUCKLIDGE W A. Comparing Images Using the Hausdorff Distance[J]. Pattern Analysis & Machine Intelligence, IEEE Transactions on, 1993,15(9):850-863.
[7]DUBUISSON M P, JAIN A K. A modified Hausdorff distance for object matching[C]//Proceedings of the 12th IAPR International Conference on Pattern Recognition, IEEE, 1994:566-568.
Fast Recognition Algorithm for Finger Vein Based on the Line Distance Order Statistics
LI Xiaogang, SHEN Lei, ZHANG Yanyan, LAN Shiwei
(SchoolofCommunicationEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
In order to improve the recognition performance of the low quality finger vein image, a fast recognition algorithm based on the line distance order statistics is proposed. The algorithm makes use of the order statistics to calculate the average of some small fine line distance, which improves the recognition performance of the finger image included fake vein. The neighborhood search algorithm based on the line distance calculation compared with the MHD point set calculation method matching point by point, which shortens the matching time largely. The experimental results show that the proposed algorithm has better performance than the widely used MHD algorithm based on feature points.
finger vein; matching recognition; MHD algorithm
10.13954/j.cnki.hdu.2017.04.005
2016-10-28
国家自然基金资助项目(61401133);中国博士后科学基金资助项目(2014M562302);浙江省新苗人才计划资助项目(2016R407069)
李小刚(1992-),男,安徽宣城人,硕士研究生,数字图像处理.通信作者:沈雷副教授,E-mail:shenlei@hdu.edu.cn.
TP391.41
A
1001-9146(2017)04-0020-05

