侧面叉车线控液压转向系统的设计与仿真

陶 平，吴洪明，唐 文，李 磊

（1.武汉科技大学，武汉 430081；2. 武汉理工大学，武汉 430080）

侧面叉车线控液压转向系统的设计与仿真

陶 平1，吴洪明2，唐 文1，李 磊2

（1.武汉科技大学，武汉 430081；2. 武汉理工大学，武汉 430080）

随着线控转向技术的发展，线控转向技术与液压技术结合的线控液压转向系统将改善车辆的转向性能。针对侧面叉车的行驶特点，设计了侧面叉车的线控液压转向系统，在分析系统工作原理基础上，建立了转向系统数学模型；提出了模糊PID控制策略，利用AMESim和Simulink对系统进行联合仿真，仿真分析结果表明，采用模糊控制系统的动态响应性能有明显提高，抗外部干扰能力加强，转角的跟随性较好，转向系统的响应速度达到了车辆实际的要求，为线控液压转向技术在叉车上的推广应用提供理论指导。

线控技术；液压转向系统；模糊控制；系统仿真

0 引言

侧面叉车属于低速行驶车辆，需要在狭窄空间内频繁转向，由于侧面叉车车身较长，转弯半径大，转向通常不灵活。为了减小侧面叉车的转弯半径，提高车辆转向操作的灵活性和行驶稳定性，需要在转向系统上进行改进。穆希辉等人[1]对全向行驶防爆侧面叉车关键技术进行了研究；张青林等人[2]针对叉车低速、转向频繁和转向性能要求高的特点，提出一种叉车转向轮转角模糊控制策略；方桂花等人[3]对工程车辆的线控液压转向系统进行了动态特性研究。线控液压转向系统是将线控转向技术和全液压转向系统相结合，具有稳定性好、控制精度高等优点。目前线控转向技术研究的主要对象是乘用车，对工程车辆的研究较少，本文以侧面叉车为研究对象，针对其转向需求，设计了侧面叉车的线控液压转向系统，并建模仿真分析，对其系统的动态特性进行了分析，为线控液压转向系统在叉车上的推广应用提供理论指导。

1 线控液压转向系统工作原理与数学模型

如图1所示，为线控液压转向系统工作原理图，转向盘的转动信号（方向盘转角）和车速传送给电子控制单元（ECU），按照相应的控制策略和控制目标，ECU进行相关运算和处理，把转角信号转换成电压信号，驱动电液比例换向阀的阀芯产生位移，从而输出相应的流量，驱使液压缸的阀芯运动产生位移，推动齿轮齿条机构运动，从而实现车轮转向[4]。转角传感器反馈当前车轮实际偏转角度，系统将车轮实际偏转角度与方向盘转角比较计算出两者的角度偏差，并转化为电信号传送到比例放大器，获取功率放大后的电压信号，从而达到闭环控制。

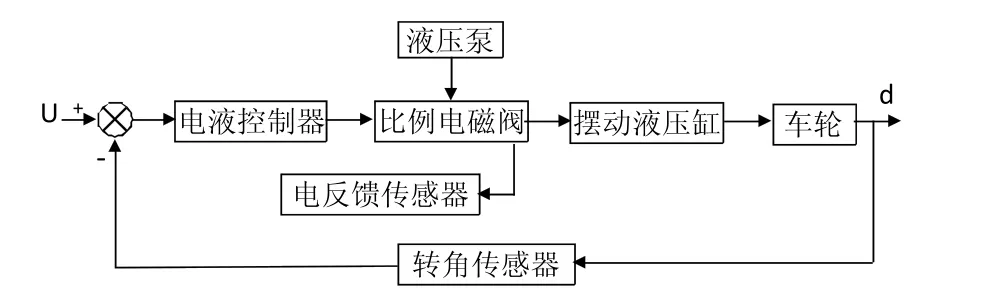
图1 线控液压转向系统工作原理

由图1可知，该系统即是一个比例阀控闭环位置控制系统，系统由比较元件、控制器、比例电磁阀、齿轮齿条摆动液压缸、车轮、转角传感器及液压泵等组成。通过对系统中各模块进行分析计算，得到各模块的传递函数[5,6]，从而获得液压转向系统的数学模型方框图如图2所示。

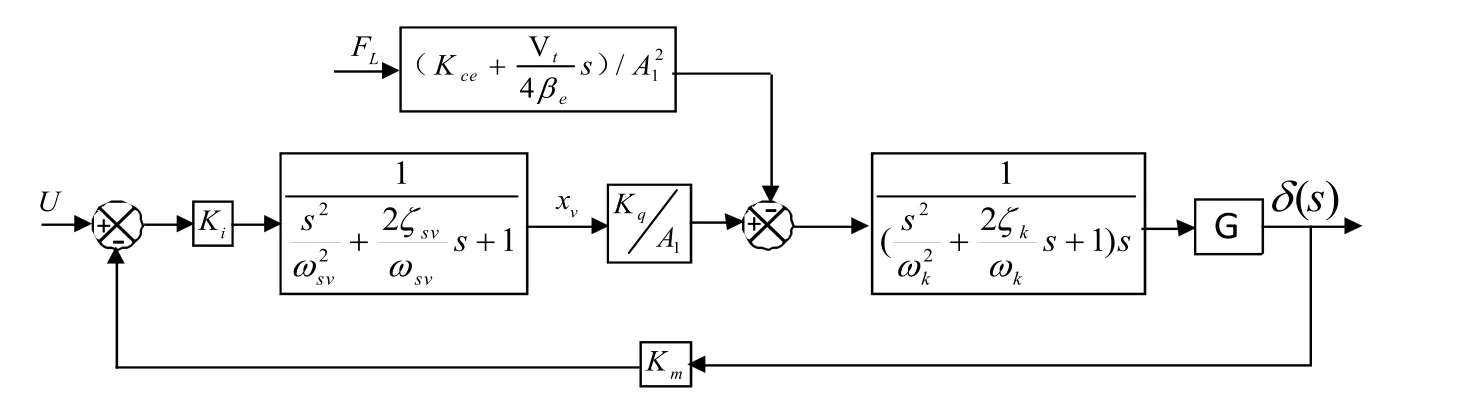
图2 液压转向系统的数学模型方框图

2 线控液压转向系统模糊控制器的设计

为保证系统的稳定性及准确性，提高系统对外界不确定因素及外负载的抗干扰能力，我们采用模糊控制算法。其控制原理[7]是将执行装置实时输出偏差e以及输出偏差变化率ec当作控制系统输入，针对不同时间不同e和ec依据模糊推理及其规则表实时完成PID参数Kp、Ti、Tp的在线修正。常规的PID调节器在获取新的整定参数后，对液压转向系统输出相应控制量。

2.1 输入、输出变量及隶属函数确定

以转向轮上转角传感器的实际输出电压信号与理想值之间的角度误差e及其误差变化率ec作为模糊控制部分的输入，而把PID控制器的修正参数ΔKp、ΔKi、ΔKd为输出量。系统的输入e、ec以及修正参数Δp、ΔKi、ΔKd的模糊论域均定义为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}，其模糊子集定义为{NB，NM，NS，ZO，PS，PM，PB}。根据前期对系统的PID参数的整定及控制经验，确定e、ec以及PID调节参数的精确论域如下：e、ec的精确论域分别为：[-5，5]， [-2，2]；修正参数ΔKp、ΔKi、ΔKd的精确论域分别为：[-0.06，0.06]，[-3，3]，[-0.0012，0.0012]。由以上各输入、输出变量的模糊、精确论域可计算出对应变量的量化因子，如表1所示。

考虑到侧面叉车转向控制系统具有有较高的控制灵敏度，其隶属函数的选定：对应前面设定的模糊子集，负大（NB）选用Z形函数，正大（PB）采用S形函数，其余五个模糊子集均选用三角形函数。

2.2 控制规则确定

要达到模糊推理规则对PID参数进行实时修正的目的，其规则依据是[8]：当输出偏差e较大时，应增加Kp值来提高系统的响应速度，减小Kd以防止其发生过饱和情况，定义Ki为0以规避出现明显的超调量。当输出偏差e适中时，应降低Kp值确保超调量变小，同时适当选取Ki和Kd的值使其获得较好的响应速度。当系统偏差e较小时，适当增加Kp，减小Ki值，使转向系统获得较好的稳定性能，并在偏差变化率ec较大时为防止转向系统出现明显震荡，减小Kd的值，反之则增加该值。

根据工程实际经验及上述规则依据，经过反复实验修正和不断调试，得出ΔKp、ΔKi、ΔKd整定的模糊规则表如表2所示。按此规则表可得到参数ΔKp、ΔKi、ΔKd的模糊值，由加权平均法[9]清晰化运算，得到ΔKp、ΔKi、ΔKd的清晰值，从而获得PID参数修正后的结果值Kp、Ki、Kd。

2.3 控制器的性能仿真分析

用Simulink搭建液压转向系统模糊控制的仿真模型图如图3所示，将侧面叉车的模型参数带入，同时进行常规PID控制仿真和模糊PID控制仿真，得到二者的仿真结果，分析比较得知，加入模糊PID控制器，系统的调整的时间从0.410秒降到了0.195秒，动态响应性能有了明显提高，基本上没有超调和震荡；在抗外负载干扰能力方面，模糊PID控制对外部干扰的抵抗能力较强，能够在更短时间内恢复到稳定状态。

表1 模糊PID控制论域参数对照表

表2 输出参数ΔKp、ΔKi、ΔKd的模糊规则表

图3 模糊PID控制器的仿真模型

3 液压转向系统的联合仿真

AMESim软件是多学科复杂系统的建模仿真平台，用AMESim可以进行液压系统和各元件的仿真研究[10]。为了提高系统仿真模型的可信度，先对系统中各关键元件如比例电磁阀、恒压变量泵、摆动液压缸等模型进行研究和测试，最后将各子模型封装，得到系统的联合仿真模型图如图4所示。

图4 液压系统的联合仿真模型

将方向盘转角作为输入量，以0～90°的斜坡输入，进行仿真得到转向轮转角及其跟踪误差，液压缸的压力、流量及输出扭矩随时间的变化情况，如图5所示。

从图5看出，转向轮的实际转角相对给定的输入转角跟踪性较好，在稳态时的转角误差约为0.772°，表明该系统的控制精度较高，转角误差率为0.86%，满足单个转向轮实际转角与理论转角相对误差不超过2%的要求；由于机械惯性和电磁惯性的作用，转向开始阶段有0.1s的延迟，在一定程度上能够避免转向响应过快。

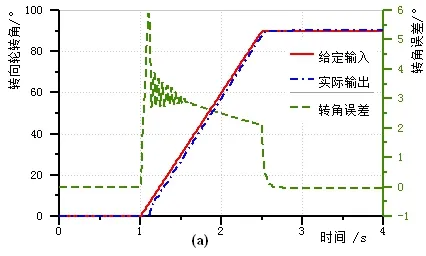
图5 转向轮转角及跟踪误差

图6 是齿轮齿条摆动液压缸两腔的压力和输出扭矩的变化情况，液压缸的压力由于比例方向阀的开启出现波动，最终稳定在8.4MPa和1.8MPa，其压差与不考虑机械效率时静态计算结果一致。

图6 液压缸压力及输出扭矩

图7 为液压缸输入流量的曲线，在启动阶段，由于压力的波动，流量波动较大，然后稳定在3.56L/min，与静态计算的结果非常接近。

图7 液压缸流量曲线

4 结论

本文以侧面叉车为研究对象，对其线控液压转向系统进行了仿真分析，分析表明采用模糊控制，系统的动态响应性能有明显提高，外部干扰的抵抗能力较强。用AMESim进行液压系统的联合仿真结果表明，转角的跟随性较好，转向系统的响应速度达到了工程实际的要求。

[1] 穆希辉.全向行驶防爆侧面叉车关键技术研究[A].物流工程高峰论坛论文集[C].2010.

[2] 张青林.叉车线控转向系统转向轮转角模糊控制策略研究[J].化工自动化及仪表,2015(8):134-136.

[3] 方桂花.工程车辆转向系统动态特性研究[J].机械设计与制造,2016(2):91-93.

[4] 朱智超,田丽娟.线控四轮转向系统的研究综述及技术总结[J].汽车技术,2012(5/6):7-12.

[5] 李磊.电动全向行驶侧面叉车转向方式的性能分析研究[D].武汉:武汉理工大学,2015.

[6] 陈永清,基于Simulink的液压闭环位置控制系统建模与仿真[J].机床与液压,2013(21):138-142.

[7] 张传红.电动助力转向系统模糊控制算法研究[J].装备制造技术,2014(2):33-35.

[8] 田福润,宋子巍.工程车转向模糊PID电液比例控制系统的设计[J].液压与气动,2011(7):32-34.

[9] 张国良.模糊控制及Matlab应用[M].西安:西安交通大学出版社,2002.

[10] 田树军,胡全义.液压系统动态特性数字仿真[M].大连:大连理工大学出版社,2012.

Design and simulation for hydraulic steering by-wire system of side forklift

TAO Ping1, WU Hong-ming2, TANG Wen1, LI Lei2

TH16

：A

1009-0134(2017)06-0023-04

2017-02-23

湖北省自然科学基金（2014CFA013）

陶平（1964 -），女，武汉人，副教授，硕士，研究方向为机电控制技术、机械设计及理论。