数控宏程序车削凹圆弧异形螺纹探索
张孟陶

(安徽阜阳技师学院机电工程系,安徽 阜阳 236000)
[摘 要] 数控车削中,异形螺纹的编程和加工有别于普通螺纹,在没有成形刀具的情况下,单纯使用固定指令手工编程或使用编程软件自动编程都很难完成,而运用数学思想,建立数学模型,编写具有逻辑运算功能的宏程序,使用常规刀具也能够車削异形螺纹,这也是当前数控车削教学中的难点。通过具体试验,可以找到车削凹圆弧异形螺纹几种较为实用的编程方法,对数控教学及技能比赛有一定的帮助。
[关 键 词] 数控;宏程序;车削;凹圆弧;异形螺纹
[中图分类号] G712 [文献标志码] A [文章编号] 2096-0603(2017)09-0117-03
一、引言
近年来,随着我国对制造业发展的重视,数控加工作为先进制造技术的典型代表,逐渐被人们所熟知。许多高职和中职院校相继开设了数控专业,为使用数控设备的企业培养数控人才,数控技能比赛也在全国各省市陆续举办。纵观近几年教育系统和人社系统举办的数控车工技能比赛,异形螺纹的车削,被作为难点项目考查参赛人员的编程和加工水平。
所谓异形螺纹是指螺纹的牙型和尺寸与普通螺纹不同的螺纹,而异形螺纹的编程和加工也有别于常见螺纹(如三角螺纹和梯形螺纹)的编程和加工。三角螺纹和梯形螺纹的加工方法通常是采用机夹成形螺纹刀,对螺纹进行直进法或斜进法加工,在FANUC数控系统下,手工编程指令一般使用单行程螺纹切削指令G32、螺纹切削单一循环指令G92、螺纹切削复合循环指令G76。另外也可以使用数控车编程软件将螺纹的大径和小径画出,通过设置软件中的加工参数,自动生成螺纹加工程序,再将程序传输到数控车床中。相对于常见螺纹固定的编程指令和简单的加工方式而言,异形螺纹的编程和加工较为复杂。无论使用哪种编程指令和编程方式,只有刀具的形状符合螺纹的牙型,才能加工出合格的螺纹。异形螺纹作为考查难点,比赛题目会尽量避免参赛选手赛前准备成形刀具,编程时采用固定指令直进法车削,而使用数控车编程软件也很难自动生成异形螺纹的加工程序,因此很多选手会感到束手无策,无从下手。本文依据试验结果,结合实物,以凹圆弧异形螺纹为例,根据图纸建立数学模型,运用高等数学中微积分的思想,使用常规刀具,在FANUC Series 0i Mate—TC数控系统下,采用宏程序的变量编程、逻辑运算和条件转移,套用固定指令的方法,从多个角度编写凹圆弧异形螺纹的加工程序。
二、试验设备、工量刃具和材料
试验使用的设备是沈阳第一机床厂生产的CAK4085di数控车床,配置的是FANUC Series 0i Mate—TC系统。工量刃具有:主偏角93°刀尖角35°的右偏外圆刀、主偏角72.5°刀尖角35°的中置外圆刀、游标卡尺、千分尺、卡盘扳手、刀架扳手、加力杆等。试验材料是45#圆钢,直径50mm。
三、分层车削法加工凹圆弧螺纹
(一)加工图纸
如图1所示,零件的主要尺寸为:圆弧螺纹外径40,长度40,圆弧半径R2,牙深1,螺距P=6。
(二)构建数学模型
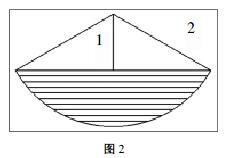
零件的外圆可以用右偏外圆刀车削,包括螺纹的外径部分,可以直接控制到40,圆弧螺纹可以使用中置外圆刀车削,单独取出一个螺纹牙进行分析,如图2所示。要完成车削,只需使用刀尖将螺纹牙中的材料去除即可,也就是让刀尖的轨迹布满螺纹牙中的空隙,利用高等数学中微积分的思想,将空隙分为若干层,刀具在每层所占的点位连成一条直线,相邻两层之间的距离足够小,这样刀尖所占的所有点即是空隙中的材料。宏观上再结合固定指令G92进行车削,即可完成凹圆弧螺纹的加工。
刀尖所在深度不同,每层左右两端的极限位置也就不同,可以构造直角三角形,利用三角函数算出极限位置的坐标。
(三)编写螺纹程序
O3;(程序名)
G00 G40 G97 G99;(程序初始化)
M03 S400 T0303;(确认主轴转速和刀位)
G00 X45.0 Z10.0;(定位循环起始点)
#1=1.0;(根据图纸定义螺纹单边牙深变量初始值)
N1 #1=#1-0.1;(每次分层切深0.1,即前面所说的相邻两层之间的距离)
#2=SQRT[2.0*2.0-[2.0-#1]*[2.0-#1]];(根据构造的直角三角形,利用勾股定理计算出每层Z方向开始切削的极限位置)
#3=#2;(定义每层从极限位置开始切削)
N3 #3=#3-0.1;(每次Z方向进刀0.1,即同一层刀尖轨迹相邻两点之间的距离)
G00 X45.0 Z[#3+10.0];(根据变量定位每一刀的切削循环起始点)
G92 X[38.0+2.0*#1] Z-40.0 F6.0;(螺纹底径38,根据牙深变量计算每层X方向直径值,利用G92循环指令车削螺纹)
IF [#3 GT -#2] GOTO 3;(建立逻辑判断语句,完成一层的循环车削)
IF [#1 GT 0.1] GOTO 1;(建立逻辑判断语句,完成所有层的循环车削)
G00 X100.0 Z100.0;(返回换刀点)
M30;(程序结束)
注:最后一层放弃不车,不能将程序写成IF [#1 GT 0] GOTO 1;如果车,机床会报警“引数指定错误”,原因是#2与#3的逻辑关系会计算错误,当车削到最后一层时,根据勾股定理计算出#2=0,此时#3是不能存在于#2和-#2之间的,即当#2=0時,不能满足-#2<#3<#2。
四、极坐标仿形车削法加工凹圆弧螺纹
(一)加工图纸
图纸同图1加工图纸
(二)构建数学模型
零件的整体加工思路与图2大致相同,同样用到高等数学中微积分的思想,都是让刀尖的轨迹布满螺纹牙中的空隙,只是在去除螺纹牙中的材料时,刀尖的轨迹组成的线路与图2有所不同。图2的是分层直线,而此方法是根据圆弧的形状组成仿形线路,如图所示。
刀尖在圆弧上任意一点的坐标可以通过在极坐标下构造直角三角形,利用三角函数表示。以最后车削的圆弧轨迹为例,以圆弧圆心为极坐标系原点,车削起始点的坐标可以用∠α表示,即起始角,终止点的坐标用∠β表示,即终止角(为编程方便∠α和∠β都是负值),也就是说刀尖轨迹组成的圆弧是从∠α到∠β,起始角和终止角之间的任意角可以用三角函数代入变量表示,而其他轨迹圆弧上的对应点可以在此基础上加一個深度变量即可表示。
(三)编写螺纹程序
O4;(程序名)
G00 G40 G97 G99;(程序初始化)
M03 S400 T0303;(确认主轴转速和刀位)
G00 X45.0 Z10.0;(定位循环起始点)
#1=1.0;(根据图纸定义螺纹单边牙深变量初始值)
N1 #1=#1-0.2;(每次仿形进刀0.2,即相邻兩条圆弧线之间的距离)
#2=-ASIN[1/2] ;(圆弧起点相对圆弧圆心的初始角,用负值表示,即图中的∠α)
N2 #2=#2-1.0;(极坐标下每次角度变化量1°)
G00 X45.0 Z[2.0*COS[#2]+10.0];(根据角度和圆弧半径,计算定位每一刀Z方向的切削循环起始点)
G92 X[42.0-2.0*ABS[2.0*SIN[#2]]+2.0*#1] Z-40.0 F6.0;(圆弧圆心位置42,根据角度、圆弧半径和牙深变量计算每条仿形轨迹X方向直径值,利用G92循环指令车削螺纹)
IF [#2 GT [ASIN[1/2]-180.0]]GOTO 2;(建立逻辑判断语句,完成一条仿形轨迹的循环车削,用反三角函数表示圆弧终点相对圆弧圆心的终止角,即∠β)
IF[#1 GT 0]GOTO 1;(建立逻辑判断语句,完成所有仿形轨迹的循环车削)
G00 X100.0 Z100.0;(返回换刀点)
M30;(程序结束)
注:因为角度变量是在负值范围内变化,而所有的长度都是正值,所以根据角度利用三角函数计算出的长度,如果是负值,之前应该加绝对值符号“ABS”,如程序中的G92一段指令。
五、直角坐标仿形车削法加工凹圆弧螺纹
(一)加工图纸
图纸同图1加工图纸
(二)构建数学模型
零件的整体加工思路与图3相同,唯一不同的是刀尖轨迹组成的仿形线路不再用极坐标下的角度变量表示,而用直角坐标下的长度变量表示,计算方法不再用三角函数,而用勾股定理,如图所示。
以最后车削的圆弧轨迹为例,以圆弧圆心为直角坐标系原点,构造直角三角形,车削起始点的坐标可以用SQRT[2.0*2.0-1.0*1.0]表示,终止点的坐标用-SQRT[2.0*2.0-1.0*1.0]表示,起始点和终止点之间的任意一点的坐标可以利用勾股定理代入变量表示,其他轨迹圆弧上的对应点可以在此基础上加一个深度变量即可表示。
(三)编写螺纹程序
O5;(程序名)
G00 G40 G97 G99;(程序初始化)
M03 S400 T0303;(确认主轴转速和刀位)
G00 X45.0 Z10.0;(定位循环起始点)
#1=1.0;(根据图纸定义螺纹单边牙深变量初始值)
N1 #1=#1-0.2;(每次仿形进刀0.2,即相邻两条圆弧线之间的距离)
#2=SQRT[2.0*2.0-1.0*1.0];(车削起始点Z方向初始值)
N2 #2=#2-0.1;(直角坐标下每次Z方向长度变化量0.1)
#3=SQRT[2.0*2.0-#2*#2];(代入变量,利用勾股定理表示任意一点X方向的长度)
G00 X45.0 Z[#2+10.0];(根据变量定位每一刀的切削循环起始点)
G92 X[42.0-2.0*#3+2.0*#1]Z-40.0 F6.0;(圆弧圆心位置42,根据牙深变量计算每条仿形轨迹X方向直径值,利用G92循环指令车削螺纹)
IF [#2 GT -SQRT[2.0*2.0-1.0*1.0]]GOTO 2;(建立逻辑判断语句,完成一条仿形轨迹的循环车削,利用勾股定理表示终止点Z方向坐标)
IF [#1 GT 0]GOTO 1;(建立逻辑判断语句,完成所有仿形轨迹的循环车削)
G00 X100.0 Z100.0;(返回换刀点)
M30;(程序结束)
六、结束语
本文探索出三种车削凹圆弧异形螺纹的宏程序编程方法,在4.3和5.3的程序中的深度变量也可在操作机床时,通过改变刀补来替代,分层车削的变化量一定要能整除牙深量。在实际加工时,可根据机床性能、刀具强度、工件刚性等适当调整切削参数,以减少空行程,提高切削效率。利用宏程序车削异形螺纹,是通过点的密集构成螺纹的轮廓线,此方法车削的螺纹表面粗糙度较差,如何提高表面质量,还有待于今后进一步试验和研究。
参考文献:
[1]沈春根,徐晓翔,刘义.数控车宏程序编程实例精讲[M].北京:机械工业出版社,2011.
[2]张运强,穆瑞.FANUC数控系统宏程序编程方法、技巧与实例[M].北京:机械工业出版社,2011.

