国际粮价波动特征及其随机冲击效应研究
——以大米价格为例
杨万江,刘琦
(浙江大学中国农村发展研究院,浙江 杭州 310058)
国际粮价波动特征及其随机冲击效应研究
——以大米价格为例
杨万江,刘琦
(浙江大学中国农村发展研究院,浙江 杭州 310058)
近年来,国际主要粮食价格波动剧烈,这对中国粮食安全保障提出了重要挑战。本文以大米为例,基于2009年至2016年泰国100% B级整精米和泰国全碎米价格月度数据,利用B-N分解法考察了国际市场粮食价格波动特征,并使用方差比统计量测定了随机冲击效应。研究结果表明:总体上,外部冲击对泰国100% B级整精米和泰国全碎米均存在正面效应,而且在此期间,泰国100% B级整精米和泰国全碎米价格波动分别经历了10个和8个完整周期;基于方差比度量的结论为:短期内,随机冲击对两种大米价格波动的影响高达1.6倍和3倍;长期来看,随机冲击对国际市场中两种大米价格长期波动所起的作用分别为6%和2%。因此,应根据当前随机冲击影响和周期波动走势,采取措施稳定粮食市场,保障国家粮食安全。
国际大米价格;B-N分解;趋势周期;随机冲击;粮食安全
Abstract:Recent years, sharply fuctuation of international major grain prices has brought signifcant challenges to China’s grain security. Based on the data of monthly prices of Thai 100% B second grade white rice and white broken rice during 2009-2016 and applying the Beveridge-Nelson decomposition method, this paper investigated the features of international grain price volatility and examined the infuences of stochastic impacts using variance ratio. Results indicate that: 1) in general, the stochastic shocks have signifcant positive infuences on the prices of both Thai 100% B second grade white rice and white broken rice; 2) during the study period, Thai 100% B second grade white rice prices experienced ten complete cycles, while white broken rice prices experienced eight; and 3) the impacts of stochastic shocks on two rice prices in the international market are 1.6 times and 3 times in the short run, and 6% and 2% in the long run, respectively. Therefore, the government should take measures to stabilize grain market and guarantee grain security according to the current impacts of stochastic shocks and cyclical trends of rice prices.
Key words:international rice prices; Beveridge-Nelson decomposition; trend cycle; stochastic shocks; grain security
过去十多年来,国际主要粮食价格剧烈波动,总体上呈现“上涨——回落——上涨”的特征,具体如下:自2006年下半年至2012年末大米价格一直在较高水平上下波动,期间分别于2008年初、2011年初和2012年第三季度出现三次粮价峰值[1];2013年第一季度粮食价格逐渐回落,并于2014年第一季度跌至谷底;而自2014年3月份以来,国际粮价又开始了新一轮的上涨。FAO公布的数据显示,谷物价格指数在1990-2000年的月度间变异系数为0.12,到2001-2008年该变异系数增加到0.28,而2009-2014年该变异系数又下降至0.13。目前,中国国内农产品价格也呈现出上涨的状态,并且,近年来中国在国际农产品市场上扮演着越来越重要的角色,农产品贸易额迅速攀升,意味着国际农产品价格可能会对中国农产品价格产生不可忽视的影响作用[2-3]。最新统计数据表明,2016年我国稻米进出口总量和额度均出现增长,当年累计进口稻米356.28万t,较上年增加5.5%,进口额超过16亿美元,较上年增加7.7%;出口稻米39.51万t,较上年增加37.6%;出口额3.51亿美元,较上年增加31.0%。因此,以国际大米价格为例,研究国际粮食价格的波动特征无疑对新形势新条件下我国粮食安全具有重要意义。
更为重要的是,粮食价格的波动不仅会影响到粮食供给的稳定性,而且还对人们的购买力水平和对粮食获取能力产生影响,使粮食安全受到威胁。随着国际粮价震荡和国内生产状况变化,现阶段中国粮食价格迅速上涨且波动剧烈,对粮农和粮商的生产经营行为造成了很大的干扰,同时通过“定价之基”的属性引发社会整体物价水平震荡,波及广大消费者基本生活[4]。因此,了解国际粮价的波动特征,如何保障国家粮食安全问题成为中国农业发展在新形势新要求下的重大考验之一。
回顾以往关于粮食价格波动的研究可以发现,大量文献主要是使用2012年之前的国际粮食价格数据来考察价格波动的原因及其影响因素。一些研究侧重于生物质能源的发展对国际粮食价格的影响,指出生物质能源发展带来的全球主要农产品市场供需结构的变化是影响国际农产品价格波动的最主要因素[5-6],或者认为粮食价格波动主要是由季节性波动和随机性波动引起,其中随机性因素作用更大[7-8]。另一些研究则关注了国际粮食市场和进出口贸易的演变造成了国际粮价的波动。比如,孙林[9]分析了2007-2008年粮食主产国出口限制对国际粮食价格的影响,认为在特定时期粮食主产国的出口限制政策推动了国际粮食价格上涨。还有一些研究考察了国际粮食价格波动对中国粮食价格波动的影响作用,其中,一种观点认为国际油价波动与国内农产品价格之间的关系长期处于线性与非线性的转换过程之中,国际油价主要是通过国内通货膨胀率、货币发行量和国际农产品价格等因素间接影响中国农产品价格[10];而另一种观点强调随着粮食市场开放程度提高,国际粮食价格波动对中国粮食价格波动具有显著的溢出效应[11]。
总的来说,关于国际粮食价格的相关研究较为丰富,但是将研究视野集中于2009年以来的国际粮食价格波动的研究尚不多见。因此,本文利用2009-2016年国际主要粮食价格(以大米为例)的月度数据,使用Beveridge-Nelson(即B-N)趋势周期分解模型考察了国际大米价格变化特征,重点从价格波动的长期趋势、周期成分和随机冲击等层面深入了解国际主要粮食价格波动,不仅为相关研究提供了进一步分析思路,也为如何在新形势下保障我国粮食安全提供了一些启示。
1 研究方法和数据来源
1.1 研究方法
本文所使用的研究方法是Beveridge和Nelson提出的B-N趋势周期分解模型[12]。该模型最初用于测量真实的“经济周期”,将非平稳时间序列分解为持久成分与短期成分。持久性成分为一个带漂移的随机游走过程,即确定性趋势和随机趋势之和;短期成分为一个零均值的平稳过程,即周期趋势。后经过Newbold[13]、Ariño和Newbold[14]、Morley[15]等学者的深入研究和扩展,最终形成了B-N分解的统一框架。本文将利用B-N趋势周期分解模型,将国际大米价格分解为长期趋势、周期成分和随机趋势,并从这三个层面把握国际粮食价格波动特性。
本文主要目标是将国际大米价格序列(yt)分解为确定性趋势(DTt)、随机趋势(STt)与周期成分(Ct)之和,即:

式中:yt为待分解的I(1)过程,其一阶差分(Δ yt)是一个平稳过程。Δyt可以表述为一个MA(∞)过程,即:

其中:μ为Δ yt的长期均值。按B-N分解理论,y0为初始时间的值,yt的确定性趋势(DTt)为:

Beveridge和Nelson[12]首先通过定义长期的水平条件期望值以表述确定性趋势与随机趋势之和,即总趋势。记 ˆyt+s|t为基于当期(t期)的所有信息为条件的未来s期的条件期望,对s→∞时进行预测,可得到:
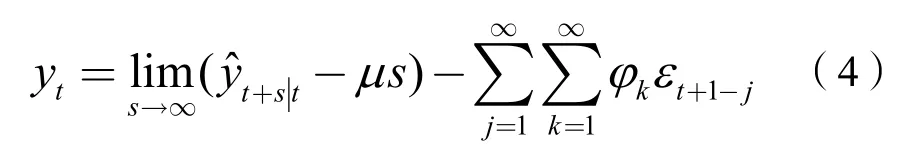
根据B-N分解对周期的定义,周期为当期的真实值与趋势值之差,故周期成分Ct表示为:

至此,从理论上说,可以直接根据式(5)计算周期即可。但是,一方面,在式(5)中出现“无穷大”一般是不可计算的,Beveridge和Nelson[12]建议取一个较大的值近似计算,显然这种计算方式既繁琐又不精确。另一方面,根据式(5)计算周期,仅利用了估计的残差信息,使计算周期的精度受到影响,为此需要进一步改进上述分解方法。
令wt=Δ yt-μ,有wt:I(0),由Wold定理可知,wt可由一个均值为零的ARMA(p,q)过程所表述。估计出结果ˆwt,代入经过一系列等式变换的周期成分表达式,最终可得周期成分Ct的计算公式为:
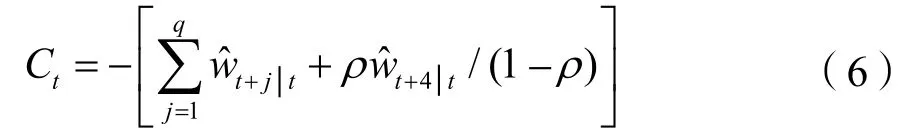
ρ为wt的AR项系数,具体推导过程可参见王少平和胡进[16]、王明利和李威夷[17]文献,在此不再赘述。
最后,根据式(1),我们可以得到随机趋势STt为:

在已将国际市场中大米价格分解为确定性趋势、随机趋势和周期成分之和的基础上,本文使用方差比统计量,揭示随机冲击对国际大米价格波动产生的影响。Cochrane定义的方差比为[18]:

本文所有模型运行均使用Eviews7.2。
1.2 数据来源
在本文中,国际市场大米价格以泰国100% B级整精米和泰国全碎米的曼谷离岸价格(FOB)为例,时间序列为2009年1月至2016年12月的月度价格,单位为美元/t,样本数为96个,数据来源于联合国粮食与农业组织(FAO)(http://www.fao. org)统计数据库。大米月度价格经过消费者价格指数(CPI)平减,消费者价格指数来源于美国劳工部统计局(http://www.bls.gov),以2009年1月为基期。考虑到大米消费的季节性因素,再对价格数据进行季度调整,并取对数,将泰国100% B级整精米价格记为y1,泰国全碎米价格记为y2。
2 结果与分析
2.1 国际市场大米价格波动变化分析
大米是世界超过半数国家、全球60%以上人口的主食,其价格走势及市场稳定受到社会各界的广泛关注。一方面,由于大米与小麦、玉米存在替代关系,大米价格的走高会导致小麦和玉米价格增加,将会导致农产品价格上升,进而传导至各部门并影响价格、产出、就业等各项指标,导致社会总体福利降低,不利于宏观经济的发展。另一方面,全球90%左右的大米出产自亚洲,大米也是全世界30亿人的主食。从粮食供应的角度来看,世界大米生产主要集中于东亚和东南亚国家。
泰国是世界最重要的大米出口国,其大米出口量对世界大米市场价格走势发挥着基础性作用。泰国出口的大米主要有六种,根据碎米率为定级指标,碎米率越高,市场交易价格越低。因此,本文选用泰国100% B级整精米价格和全碎米价格分别代表高价位的高档食用米和低价位的低档食用米,进而来反映国际大米价格的变化。
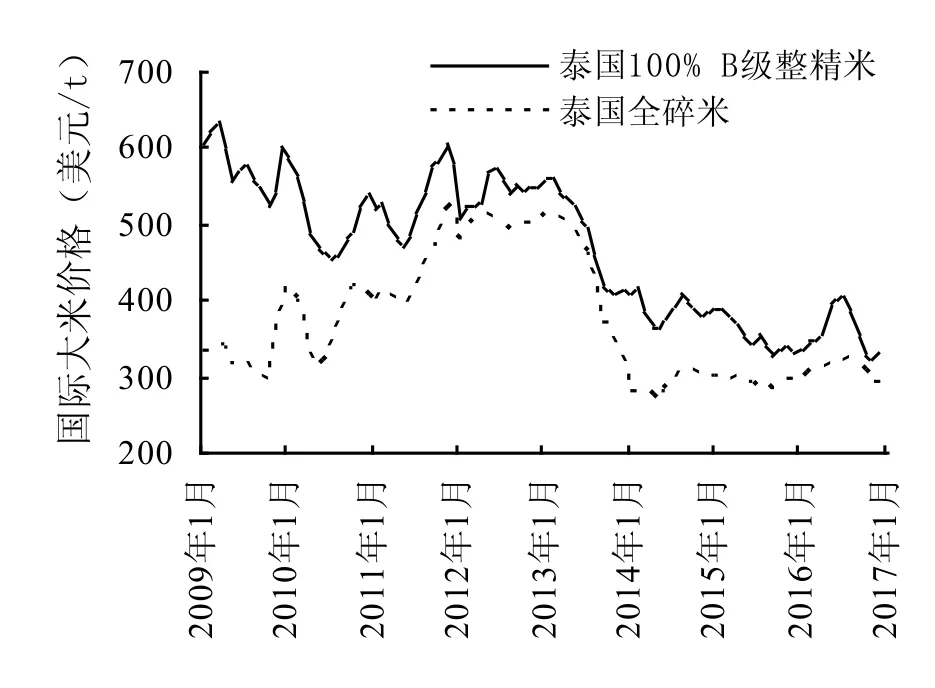
图1 2009年1月-2016年12月国际市场大米价格Fig. 1 International rice prices from January 1990 to December 2016
图1展示了2009年1月至2016年12月期间国际大米价格波动的变化,表1对两种大米价格进行了描述性统计分析。需要说明的是,图中价格是以2009年1月为基期并利用消费者价格指数(CPI)进行了平减。由图1可知,在2009年1月至2010年6月期间,无论是泰国100% B级整精米价格,还是全碎米价格均逐月下跌,其中整精米价格跌幅最为明显,到2014年6月跌至453.66美元/t。从2010年6月到2014年6月,整精米和全碎米的价格走势呈“钟形”,以2012年为对称轴,两种大米价格均是先上升,后下降,变化趋势基本一致。2015年1月开始,泰国100% B级整精米价格波动剧烈,先是迅速下降,接着于2016年5月迅速上涨,尔后于当年7月达到顶峰值(约为400美元/t),在此之后又进入新一轮的“跌——涨”周期。与此同时,全碎米价格基本呈现出稳中略涨的态势。结合图1和表1可知,在2009年1月至2016年12月期间,泰国100% B级整精米的平均价格约为468.21美元/t,价格最高时(2009年3月)为635.32美元/t,2016年11月下降到最低时为322.89美元/t。泰国全碎米的平均价格约为370.33美元/t,2011年12月时价格最高,约为522.50美元/t,2014年5月价格下降至最低约为267.03美元/t。反映两种大米价格序列波动离散程度的标准差分别约为90.25和82.43,说明泰国100% B级整精米价格比泰国全碎米价格的波动更剧烈。

表1 国际市场大米价格描述性分析Table 1 Statistical description of international rice prices
2.2 趋势周期分解结果分析
国际大米价格是否为趋势平稳过程,直接关系到周期分解的方法和结果。如果国际大米价格是趋势平稳过程,早期的趋势周期分解是直接从价格序列中退化趋势。显然,这种分解周期和趋势的方法,潜在地排除了价格中的随机趋势。由于国际大米价格不是趋势平稳过程(检验结果见表2),因此这一方法不适用于分解国际大米价格的趋势与周期。另一方面,图2为国际大米价格的月度增长速度(Δ yt)趋势线,尽管增长速度部分地反映了随机冲击对价格变化的影响,但是基于价格变化划分周期,其本质依赖于“拐点”。显然,图2的“拐点”过多,也无法全部反映出由随机冲击所形成的随机趋势。因此,基于价格增长速度无法划分出真正的周期。
基于上述两点,我们采用B-N趋势周期分解,但首先需要检验国际大米价格的数据是趋势平稳过程还是由I(1)过程所生成。对图2所示的数据,通过KPSS平稳性检验和ADF单位根检验这两种方法,本文验证了国际大米价格的时间趋势性,所有检验结果见表2。
由表2可知,国际大米价格不是一个趋势平稳过程,而是非平稳的I(1)过程,这一结论表明了国际大米价格包含有随机趋势。另外,两种国际大米价格的ADF检验结果中截距项均显著不为0,这一结果不仅表明两种国际大米价格均是带截距项的I(1)过程,也说明其价格序列中均包含确定性趋势。进一步,ADF检验结果中,显著的差分滞后项代表一种短期的调整行为,这说明两种国际大米价格序列存在一个平稳的随机过程,即真实的周期成分。由以上检验结果与分析可知,两种国际大米价格是带有截距项的I(1)过程而不是趋势平稳过程,因此可以对其进行趋势周期分解。
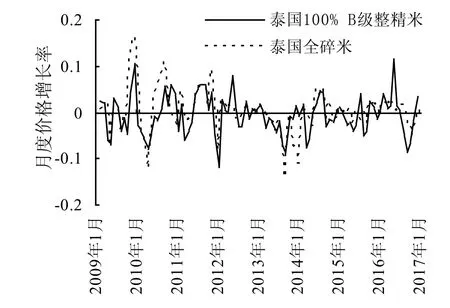
图2 国际大米价格月度增长率Fig. 2 Monthly growth rates of international rice prices

表2 国际大米价格序列的平稳性检验和单位根检验Table 2 Time trend stationarity test and unit root test of international rice prices
2.3 国际大米价格的确定性趋势
经计算和整理,整精米价格y1和全碎米价格y2的初始值分别为6.377和5.770,一阶差分的长期均值μ1和μ2分别为-0.006和-0.001。根据式(3)计算出确定性趋势(DTt),其全部结果见图3。为方便分析,我们将计算的确定性趋势月度数据转换为年度数据,进而计算确定性趋势的年度值占实际价格的比例,记这一比例为St(St=DTt⁄yt),其结果列入表3。S1t表示泰国100% B级整精米,S2t表示泰国全碎米。
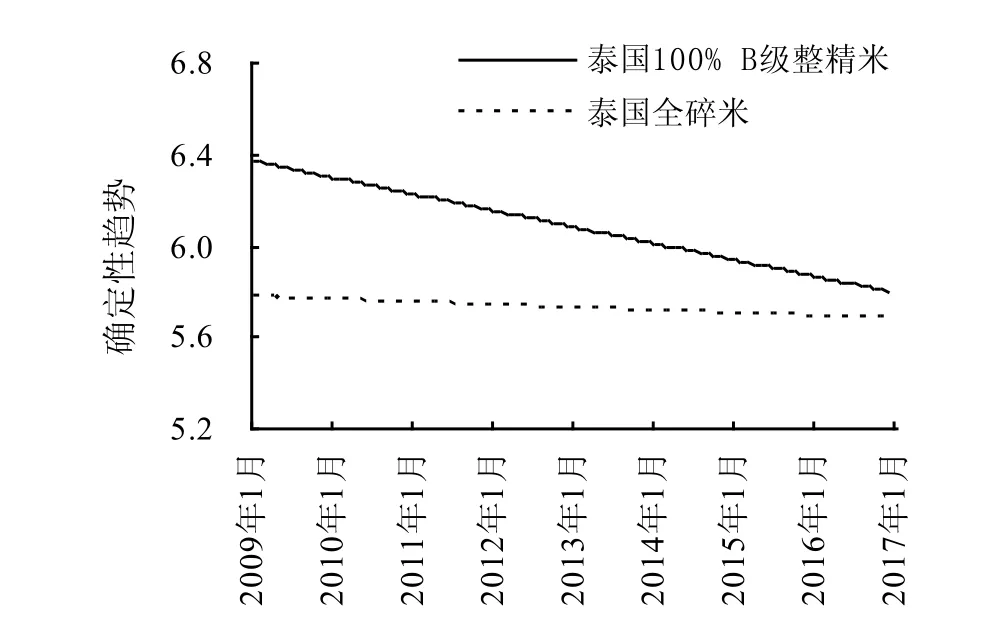
图3 泰国100% B级整精米和泰国全碎米价格的确定性趋势Fig. 3 Deterministic trend of Thai 100% B second grade white rice and white broken rice prices
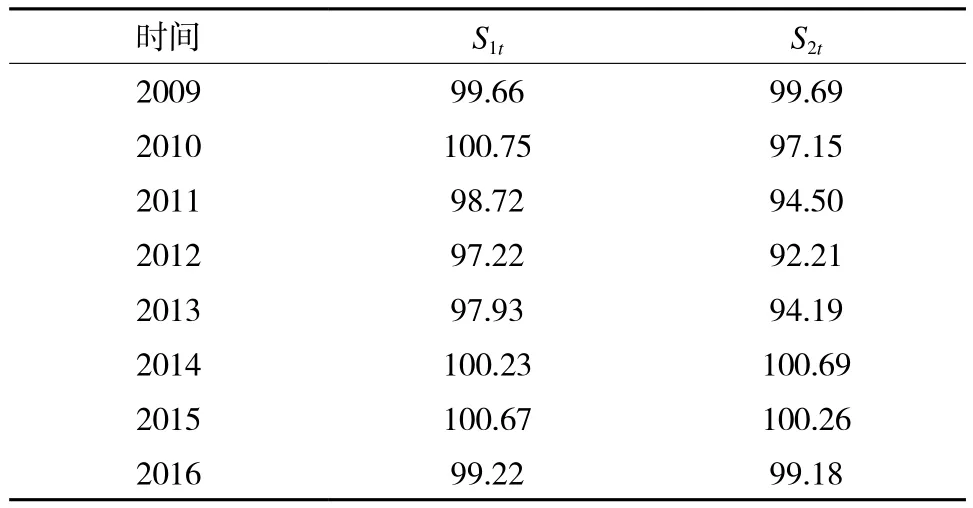
表3 泰国100% B级整精米和泰国全碎米价格确定性趋势占价格比重(%)Table 3 Ratio of deterministic trends of Thailand 100% B grade whole rice and white broken rice prices (%)
分解结果表明,泰国100% B级整精米和泰国全碎米的价格均有稳定下降的确定性趋势,但泰国100% B级整精米的下降趋势较大,泰国全碎米的下降趋势较小。具体来看,泰国100% B级整精米价格的确定性趋势占实际价格比例的波动较小,平均比值达到99.30%,而泰国全碎米的确定性趋势占实际价格比例波动较大,平均比例为97.23%。
由于实际价格中也包含了随机冲击及其累计的效应等,因此确定性趋势形成的值可能大于或小于当期实际价格,表现为St可能大于或小于100%。当St大于100%,说明随机冲击对价格有抑制作用,反之说明随机冲击具有促进价格增长的作用。观察表3发现,2010年S1t值大于100%,S2t的值小于100%,说明随机冲击效应对泰国100% B级整精米的实际价格有抑制减少的作用,对泰国全碎米的实际价格有促进增长作用;2014年和2015年S1t的值和S2t的值均大于100%,除此外,其余年份S1t的值和S2t的值均小于100%,特别是2012年,说明随机冲击效应对实际价格有促进增长的作用。
2.4 国际大米价格的周期成分
2009年以来,国际市场上的泰国100% B级整精米和泰国全碎米的价格经历了多次上涨和下跌,波动是常态化的趋势。根据前文分析,wt是I(0)过程,可由一个均值为零的ARMA(p,q)过程所表述,经过多次估算比较,整精米w1t和全碎米w2t的最优ARMA(p,q)的估计结果如下:
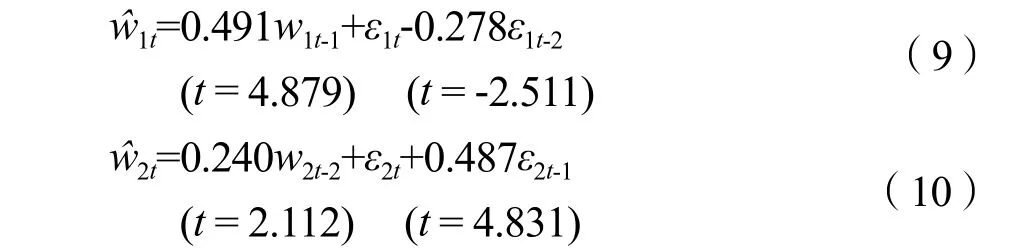
其中,ŵ1t和ŵ2t分别为整精米和全碎米的ARMA(p,q)估计值。由此,根据式(6)计算出泰国100% B级整精米和泰国全碎米价格的周期成分,如图4所示。
确定一次波动的完整周期,可以从一个波峰到另一个波峰,也可以从一个波谷到另一个波谷,或者按照周期中同样状态的平均值来衡量。本文选择“峰—峰”法划分,在2009年至2016年的96个月中,整精米的价格波动大体经历了10个周期,波动的平均周期长度约为8.7个月;而全碎米的价格波动经历了8个周期,波动的平均周期长度为10.5个月(表4)。
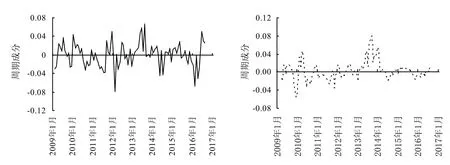
图4 泰国100% B级整精米(左)和泰国全碎米(右)价格的周期成分Fig. 4 Cyclical trends of Thai 100% B second grade white rice (left) and white broken rice (right)
从总体来说,整精米价格波动周期较短,小幅波动较多,但波动幅度不大。而全碎米价格波动周期比整精米波动周期长两个月左右,波动幅度较大。
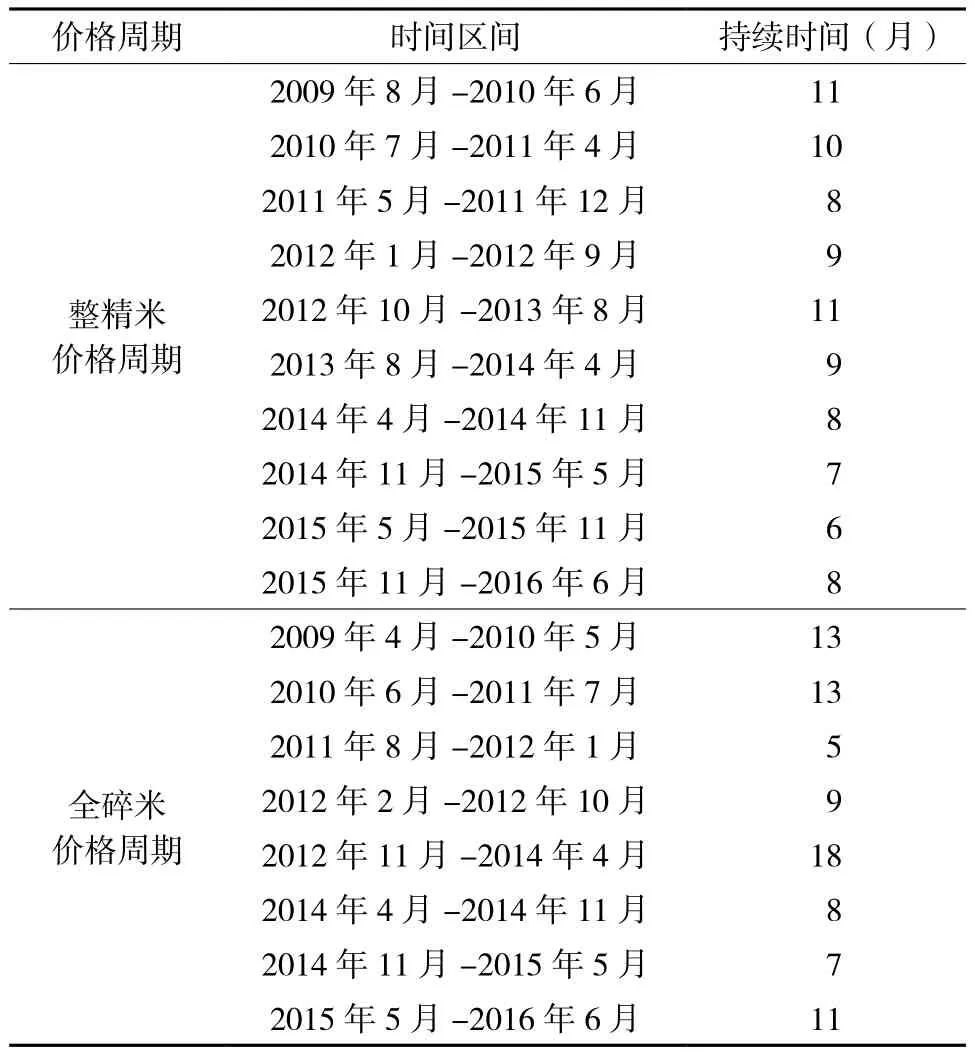
表4 泰国100% B级整精米和泰国全碎米的价格周期Table 4 Ratios of cyclical trends of Thailand 100% B grade whole grain and white broken rice
2.5 国际大米价格的随机成分
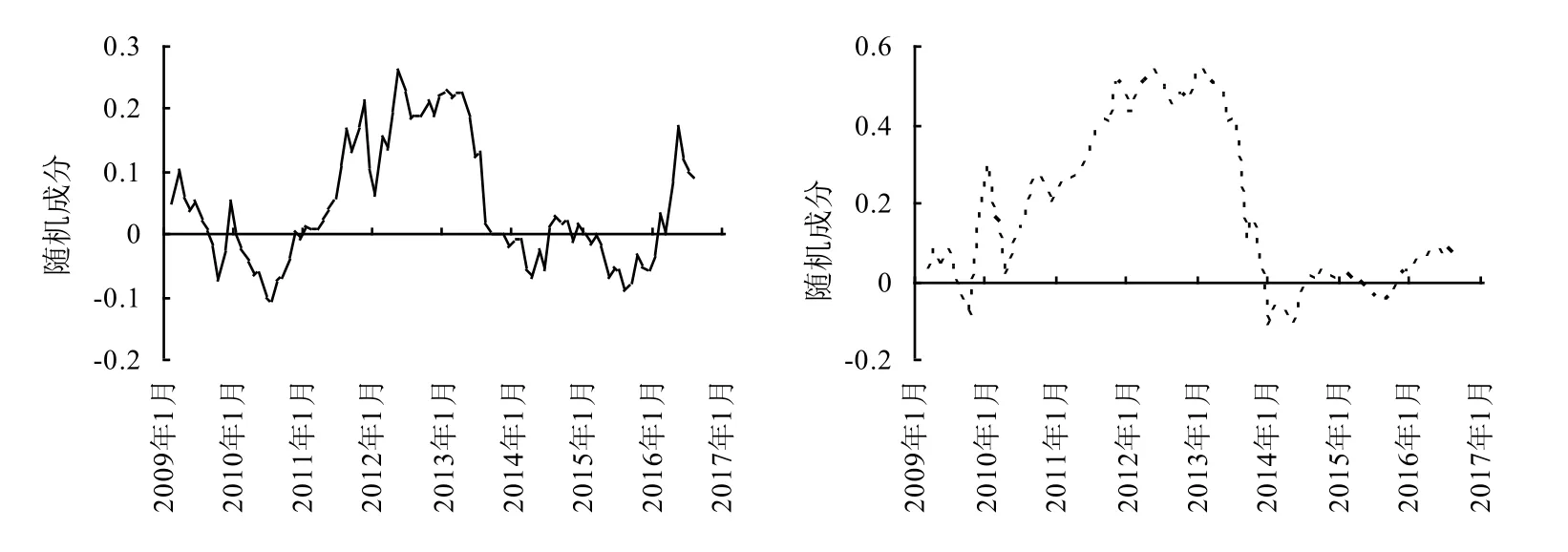
图5 泰国100% B级整精米(左)和泰国全碎米(右)价格的随机成分Fig. 5 Stochastic trends of Thai 100% B second grade white rice (left) and white broken rice (right)
由前文分析得,国际大米价格频繁遭受随机冲击,随机冲击对价格波动造成正向作用的,随机趋势值在数量上表现为正值;随机冲击对价格波动造成负向作用的,随机趋势值在数量上表现为负值。由随机游走所描述的随机趋势正是各类随机冲击对国际大米价格波动的累积效应。借助B-N分解方法,本研究具体度量了国际大米市场上泰国100% B级整精米和泰国全碎米价格的随机趋势。
根据式(7)所计算的结果如图5所示,随机成分值占价格的百分比的月度数据结果如表5所示。

表5 泰国100% B级整精米和全碎米价格随机性趋势占价格比重(%)Table 5 Ratios of stochastic trends of Thai 100% B second grade white rice and white broken rice (%)
根据式(7)计算的结果进一步分析,泰国100% B级整精米随机趋势样本期间的月度均值是0.046,标准差为0.098,样本期间各月度的随机趋势值占当期价格比的均值为0.732%。样本期间泰国全碎米随机趋势的月度均值是0.180,标准差为0.207,各月度的随机趋势值占当期价格比的均值为2.938%。从整体上看,不管是整精米还是全碎米,随机冲击对国际市场的价格产生了较大的正效应。分年度来看,在8 a间,泰国100% B级整精米所经历的随机冲击,对价格产生的正效应大于负效应,而对于全碎米,绝大部分年份所经历的随机冲击,对国际大米价格产生正效应,且效应越来越大。
2.6 随机冲击对国际粮食价格的持久性效应
本文已将国际市场中大米价格分解为确定性趋势、随机趋势和周期成分之和,而随机趋势在很大程度上影响大米价格的波动。由此提出的问题是,如何度量随机冲击对国际大米价格的波动产生的影响?本文使用方差比统计量,以揭示随机冲击对国际大米价格波动产生的影响。分别计算y1t和y2t的Rk值,以k为横轴,Rk为纵轴做出图6。
由图6可知,随机冲击不仅对国际市场大米价格具有重要的影响作用,而且对两种大米价格波动还产生了不同的影响。当期一次外部冲击对泰国100% B级整精米的影响会在以后的4个月及12个月时达到两个较高点,其Rk值分别达到1.59和1.24后减弱,随着时间推移R值收敛于0.06。而随机冲击对泰国全碎米价格波动的影响程度更大,影响时间更长。外部冲击发生后的第26个月时对泰国全碎米价格影响达到最大,其Rk值达到3.01后逐渐减弱,最后R值收敛于0.02左右。
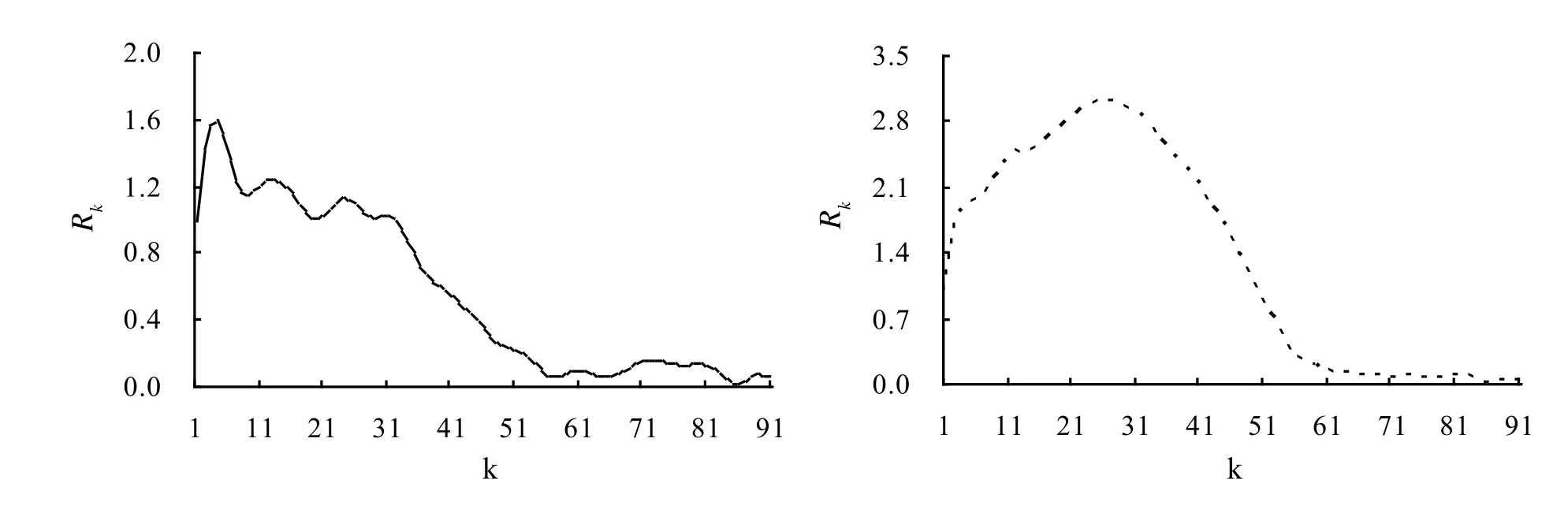
图6 随机冲击对泰国100% B级整精米(左)和泰国全碎米(右)价格的持久性影响Fig. 6 Impacts of stochastic trends on Thai 100% B second grade white rice (left) and white broken rice (right)
由以上分析得到的结论和意义为:从短期来看,随机冲击对泰国100% B级整精米和泰国全碎米价格波动的影响分别高达1.6倍和3倍,也就是说,国际市场中泰国100% B级整精米和泰国全碎米价格在特定时期的波动和周期的形成,是由随机冲击所加剧引起的。倘若拓展至长期范围内来观察,R值分别收敛于0.06和0.02,即随机冲击对国际市场中泰国100% B级整精米和泰国全碎米价格长期波动所起的作用分别为6%和2%。这一结果说明,随机冲击不仅加剧了大米价格的波动和周期形成,且随机趋势对价格的影响具有持久性而不是衰减为0。
3 结论
本文主要利用2009年1月至2016年12月国际大米市场泰国100% B级整精米和泰国全碎米月度价格数据考察了国际粮食价格波动特征,并运用B-N趋势周期分解技术对泰国100% B级整精米和泰国全碎米价格分解为确定性趋势、周期成分和随机趋势,并基于方差比统计量测度了随机冲击对国际市场大米价格波动产生的影响,结论如下:
1)国际大米市场上,泰国100%B级整精米价格和泰国全碎米价格均存在平稳下降的确定性趋势。
2)泰国100% B级整精米和全碎米存在正的随机趋势。这一结果说明外部冲击对价格产生的正面效应,是影响价格波动和周期形成的最重要原因。特别地,近几年随机冲击对价格产生正面效应越来越大。
3)泰国100% B级整精米和泰国全碎米月度价格序列存在显著的周期成分。以一个基本的U型界定周期,2009-2016年泰国100% B级整精米经历了10个完整周期,周期平均长度为8.7个月,到2016年底,基本完成新一轮周期。而泰国全碎米在此期间共经历了8个完整周期,周期平均长度为10.5个月。随着上一轮周期的结束,泰国全碎米正处于新一轮周期中。
4)本文计算的R值分别收敛于0.06和0.02,这说明泰国100% B级整精米价格长期波动中约有6%来源于随机冲击,泰国全碎米价格长期波动中约有2%来源于随机冲击。
4 启示
上述研究结论对今后一段时间内如何保障我国粮食安全具有重要的启示意义。本文的研究结果已经显示,随机冲击不仅在短期对国际市场中两种大米价格波动造成剧烈影响,且这种影响具有持久性。因此,应根据当前随机冲击影响和周期波动走势,注重自然灾害等随机冲击对粮食市场的干扰,相机抉择出台稳定市场措施,稳定粮食市场价格,保障国家粮食安全。具体来说,一是要深入推进农业供给侧改革,积极提高农业生产效率,调整农业生产结构,提高农业经营的比较效益以吸引资本、高素质劳动力等优质生产要素的流入。二是要发展双边粮食领域合作,特别是随着“一带一路”战略的深化推进,充分利用国内和国外两个市场,扩大粮食进口来源,完善我国粮食贸易的市场环境。
[1] Martin W. Managing high and volatile food prices[R]. International Agricultural Trade Research Consortium, 2012.
[2] 王孝松, 谢申祥. 国际农产品价格如何影响了中国农产品价格?[J]. 经济研究, 2012(3): 141-153.
Wang X S, Xie S X. How do prices of foreign agricultural products affect prices of Chinese agricultural products?[J]. Economic Research Journal, 2012(3): 141-153.
[3] 高帆, 龚芳. 国际粮食价格是如何影响中国粮食价格的[J]. 财贸经济, 2012(11): 119-126.
Gao F, Gong F. How international grain price affects grain price of China?[J]. Finance & Trade Economics, 2012(11): 119-126.
[4] 李剑, 宋长鸣, 项朝阳. 中国粮食价格波动特征研究——基于X-12-ARIMA模型和ARCH类模型[J]. 统计与信息论坛, 2013, 28(6): 16-21.
Li J, Song C M, Xiang C Y. Analysis on the price fuctuation of grain product in China: Based on the X-12-ARIMA model and the ARCH-type models[J]. Statistics & Information Forum, 2013, 28(6): 16-21.
[5] 胡冰川, 徐枫, 董晓霞. 国际农产品价格波动因素分析——基于时间序列的经济计量模型[J]. 中国农村经济, 2009(7): 86-95.
Hu B C, Xu F, Dong X X. Analysis on the price fluctuation of international grain product: Based on time series data[J]. Chinese Rural Economy, 2009(7): 86-95.
[6] 黄季焜, 杨军, 仇焕广, 等. 本轮粮食价格的大起大落:主要原因及未来走势[J]. 管理世界, 2009(1): 72-78.
Huang J K, Yang J, Qiu H G, et al. The analysis on grain price fuctuation on 2006-2008: Main reasons and trend in the future[J]. Management World, 2009(1): 72-78.
[7] 石自忠, 胡向东. 随机冲击对中国粮食价格波动的影响[J]. 华中农业大学学报: 社会科学版, 2015(2): 33-40.
Shi Z Z, Hu X D. Analysis of stochastic impact on grain price in China[J]. Journal of Huazhong Agricultural University (Social Sciences Edition), 2015(2): 33-40.
[8] 公茂刚, 王学真. 国际粮价波动规律及对我国粮食安全的影响与对策[J]. 经济纵横, 2016(3): 111-118.
Gong M G, Wang X Z. The impact of international grain price fluctuation and China’s food security[J]. Economic Review, 2016(3): 111-118.
[9] 孙林. 粮食主产国出口限制是否推动了国际粮食价格上涨?——以大米为例的实证分析[J]. 中国农村经济, 2011(9): 86-94.
Sun L. Whether the export restrictions of main grain production countries have promoted international grain price: An empirical analysis of rice[J]. Chinese Rural Economy, 2011(9): 86-94.
[10] 陈宇峰, 薛萧繁, 徐振宇. 国际油价波动对国内农产品价格的冲击传导机制: 基于LSTAR模型[J]. 中国农村经济, 2012(9): 74-87.
Chen Y F, Xue X F, Xu Z Y. The impact mechanism of international oil price fuctuation on domestic agricultural product price: Based on LSTAR model[J]. Chinese Rural Economy, 2012(9): 74-87.
[11] 李光泗, 曹宝明, 马学琳. 中国粮食市场开放与国际粮食价格波动——基于粮食价格波动溢出效应的分析[J]. 中国农村经济, 2015(8): 44-52.
Li G S, Cao B M, Ma X L. The opening of China’s grain market and the fuctuation of international grain price: Based on spillover effect of grain price fluctuation[J]. Chinese Rural Economy, 2015(8): 44-52
[12] Beveridge S, Nelson C R. A new approach to decomposition of economic time series into permanent and transitory components with particular attention to measurement of the ‘Business Cycle’[J]. Journal of Monetary Economics, 1981, 7(2): 151-174.
[13] Newbold P. Precise and effcient computation of the Beveridge-Nelson decomposition of economic time series[J]. Journal of Monetary Economics, 1990, 26(3): 453-457.
[14] Ariño M A, Newbold P. Computation of the Beveridge-Nelson decomposition for multivariate economic time series[J]. Economics Letters, 1998, 61(1): 37-42.
[15] Morley J C. A state-space approach to calculating the Beveridge-Nelson decomposition[J]. Economics Letters, 2002, 75(1): 123-127.
[16] 王少平, 胡进. 中国GDP的趋势周期分解与随机冲击的持久效应[J]. 经济研究, 2009(4): 65-76.
Wang S P, Hu J. Trend-cycle decomposition and stochastic impact effect of Chinese GDP[J]. Economic Research Journal, 2009(4): 65-76.
[17] 王明利, 李威夷. 生猪价格的趋势周期分解和随机冲击效应测定[J]. 农业技术经济, 2010(12): 68-77.
Wang M L, Li W Y. Trend-cycle decomposition and stochastic impact effect of pigs prices[J]. Journal of Agrotechnical Economics, 2010(12): 68-77
[18] Cochrane J H. How big is the random walk in GNP?[J]. Journal of Political Economy, 1988, 96(5): 893-920.
(责任编辑:王育花)
International grain price volatility and its stochastic impacts: A case study of rice prices
YANG Wan-jiang, LIU Qi
(China Academy of Rural Development, Zhejiang University, Hangzhou, Zhejiang 310058, China)
F304.2 文献标识码:A 文章编号:1000-0275(2017)04-0589-08
10.13872/j.1000-0275.2017.0059
杨万江, 刘琦. 国际粮价波动特征及其随机冲击效应研究——以大米价格为例[J]. 农业现代化研究, 2017, 38(4): 589-596. Yang W J, Liu Q. International grain price volatility and its stochastic impacts: A case study of rice prices[J]. Research of Agricultural Modernization, 2017, 38(4): 589-596.
国家水稻产业技术体系专项经费资助(CARS-01-10B)。
杨万江(1958-),男,四川绵阳人,博士、教授,主要从事水稻产业经济研究,E-mai:wjyang@zju.edu.cn;刘琦(1990-),女,河南郑州人,博士研究生,主要从事水稻产业经济研究,E-mail:qi-liu@zju.edu.cn。
2017-03-01,接受日期:2017-05-31
Foundation item: China Agriculture Research System (CARS-01-10B).
Corresponding author: YANG Wan-jiang, E-mail: wjyang@zju.edu.cn.
Received 1 March, 2017;Accepted 31 May, 2017

