适用于混合仿真的戴维南等值阻抗改进求取算法

杨 洋， 孙 静， 杨培栋，肖湘宁， 潘明明

(1. 国网河北省电力公司经济技术研究院，河北 石家庄 050021；2. 国网石家庄供电公司，河北 石家庄 050000；3. 国网邢台供电公司，河北 邢台 054001；4. 新能源电力系统国家重点实验室(华北电力大学)，北京 102206；5. 中国电力科学研究院，北京 100192)



·电网技术·

适用于混合仿真的戴维南等值阻抗改进求取算法

杨 洋1， 孙 静2， 杨培栋3，肖湘宁4， 潘明明5

(1. 国网河北省电力公司经济技术研究院，河北 石家庄 050021；2. 国网石家庄供电公司，河北 石家庄 050000；3. 国网邢台供电公司，河北 邢台 054001；4. 新能源电力系统国家重点实验室(华北电力大学)，北京 102206；5. 中国电力科学研究院，北京 100192)

由于基于机电暂态数据获得的机电侧系统戴维南等值阻抗参数难以体现接口发生故障后机电侧系统的电磁暂态特性，文中提出了一种基于电磁暂态短路仿真的机电-电磁暂态混合仿真机电侧戴维南等值阻抗改进求取算法。该算法是基于一种不受各次谐波影响的系统时间常数求取方法，通过全电磁暂态模型的接口位置设置2次不同接地电阻的三相短路故障，联立时间常数方程计算得到机电侧系统的等值阻抗信息。与传统的基于机电暂态模型通过单位电流注入法计算出的等值阻抗相比，文中方法计算出的等值阻抗能够更准确地体现接口发生接地故障后机电侧系统的电磁暂态特性，从而提升了机电-电磁暂态混合仿真故障期间和故障后的仿真精度。

等值阻抗；时间常数；机电-电磁；混合仿真；精度

0 引言

随着我国特高压直流建设的不断推进[1-5]，传统输电网呈现交直流混联的显著特征，直流和交流系统相互影响、紧密耦合，在增加了电网仿真分析的建模难度同时制约了其仿真效率。此外，以四象限全控型逆变装置为显著特色的分布式电源在电网中广泛应用给传统配电网的运行方式带来深刻变革。未来电网的仿真逐渐朝多时间尺度、多空间尺度和电力流与信息流相结合的方向发展，传统的、已然成熟的电力系统仿真工具，在快速发展的电力工业面前，其仿真能力和精度水平日益呈现捉襟见肘之势。

机电-电磁暂态混合仿真作为结合电磁暂态仿真和机电暂态仿真既有研究成果以保证全局仿真规模化和局部仿真精细化的有效手段，自提出以来就受到学术界和工程界的广泛关注。1982年，新英格兰电力公司(New Zealand Electricity)的Herffman[6]等人为了研究直流换流器的动态特性，在机电暂态程序中引入电磁暂态计算过程，当电磁侧发生故障之后，直流系统的电磁暂态程序启动，利用其仿真结果对机电程序对应的直流部分的结果进行修正，从而提高了故障期间机电暂态的计算精度。文献[7]和文献[8]在国内较早系统地研究了机电-电磁暂态混合仿真的相关问题，二者均考虑到了外部等值电路正序和负序等值阻抗不等所引起的不对称等值导纳阵的求解，分别提出采用节点分裂法以及戴维南电势补偿的方式进行解决。此后，中国电科院刘文焯等人[9]通过在诺顿等值电路中附加负序等值导纳与正序等值导纳不等引起的电流源来修正外部等值导纳阵的不对称。基于现有的文献，将外部系统进行戴维南(或者诺顿)等值，是解决外部系统等值的普遍思路。求取戴维南等值阻抗的一般做法是利用外部系统的机电暂态数据获得外部系统节点导纳矩阵，然后利用单位电流注入法或导纳矩阵求逆得到接口处看入的戴维南等值阻抗[10]。考虑到机电暂态建模方法与电磁暂态建模方法存在差异，这种求取方法一定程度上扭曲了外部系统实际的电磁暂态特性，从而制约了机电-电磁暂态混合仿真精度的进一步提升。

与传统的通过机电暂态数据进行戴维南等值阻抗求解的方法相比，本文提出的方法获得的等值阻抗更加接近外部系统的电磁暂态特性，从而进一步提高了机电-电磁暂态混合仿真故障期间和故障后的仿真精度。

1 机电暂态仿真和电磁暂态仿真建模差异分析

机电暂态仿真基于工频正弦波的假设条件，系统由三相网络经过线性变换为相互解耦的正、负、零序网络分别计算，系统变量采用基波相量表示，系统元件模型采用相量方程线性表示。电磁暂态仿真在建模过程中，采用ABC三相瞬时值表示，其元件模型采用网络中广泛存在的电容、电感等元件构成微分方程或偏微分方程描述。典型元件的建模方法对比如表1所示。

表1 机电和电磁暂态模型对比Table 1 The comparison of electromechanical and electromagnetic transient model

从比较中可见，机电暂态仿真在建模过程中只考虑了发电机的微分方程，对系统中大量存在的输电线路、变压器、负荷等元件只进行了稳态建模，其数学模型简化为代数方程，忽略了这些元件的电磁暂态过程，即没有考虑这些元件的非线性特性。如果将机电暂态获得的戴维南阻抗结果施加给机电-电磁暂态混合仿真，在接口处发生大扰动(如接地故障)时，等值电路的电磁暂态特性将与原外部系统的电磁暂态特性存在差异。

2 短路故障电流成分分析

本文提出了基于全电磁暂态仿真短路计算提取外部系统等值阻抗的方法。首先，为了确定短路电流特征与等值阻抗之间的关系，建立如图1所示的单相短路电流计算模型。

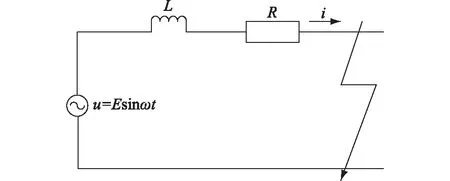
图1 短路计算模型Fig.1 Simulation model of short-circuit current

发生接地短路故障后，电压和电流的关系为:

(1)

进行拉式变换可得:

(2)

求解可得:

(3)

进行拉式反变换可得:

(4)

式(4)中:τ=L/R;φ=arctan(ωL/R)。

式(4)表明，发生短路故障后的短路电流包含2部分分量，一部分是以为时间常数进行衰减的直流分量，另一部分对应正弦分量。其中，定义τ为系统的一次时间常数。由于故障设置的时间较短，可以近似认为故障期间机电侧系统的等值电势保持不变，因此，等值阻抗的幅值决定了故障期间短路电流中直流分量和交流分量的幅值，而等值电抗ωL与等值电阻R的比值决定了短路电流正弦量的初相位，等值电感L与等值电阻R的比值决定了短路电流衰减直流分量的衰减特性。通过提取短路电流的特性参数，即可以获取外部系统等值阻抗的信息。本文选取短路电流中衰减直流分量的时间常数τ作为短路电流的特征参数，通过求取时间常数来定量计算外部系统的等值阻抗。

3 系统时间常数求取方法

文献[11]提出了一种求取外部系统时间常数的方法，其基本思路是通过对短路电流进行半个周波的延时后求和得到直流分量，然后对直流分量进行求自然对数获得时间常数。

对式(4)中的延时半个周波并与原电流进行求和，利用工频交流分量在半个周波内幅值相等而负号相反的特点对交流分量进行滤波可得：

(5)

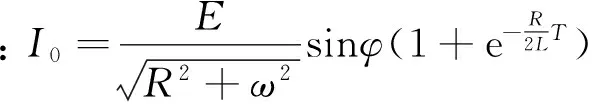
对i0(t)求自然对数，得:

(6)

从式(6)可见，lni0(t)与t成一条直线，该直线斜率的绝对值为1/τ。

分析可知，当系统中含有3，5，7等奇数次谐波时，不会影响该方法的适用性，但是故障后由于凸极同步发电机的磁路不对称，系统中也含有2，4，6等偶数次谐波，此时该方法存在不足。其主要原因是偶数次谐波经过半波延时滤波后并不能有效滤除，仍然存留在i0(t)中。以系统中含有2次谐波为例，经过滤波后可得:

(7)

式(7)中:I2为2次谐波分量的幅值;φ2为2次谐波分量的相位。

式(7)表明，当短路电流中叠加二次谐波分量后，经半波延时滤波得到的直流分量中也叠加了一个2倍频分量，取对数后得到的结果将不再是一条直线，从而影响到时间常数的求取。针对此，本文提出一种考虑各频次谐波分量的求取时间常数的改进方法。设短路电流的表达式为:

(8)

(9)

式(9)中:H0为与t无关的常数。

对h(t)进行求取自然对数得到以-1/τ为斜率变化的直线，从而计算出τ。从式(9)可知，由于在积分过程中考虑了偶数次谐波的影响，因此计算得到的时间常数更为精确。为了验证这一点，设短路电流为:

sin(200πt)+sin(300πt)

(10)

实际的电网中，故障后电流的谐波分量不会如式(10)有如此大的比例，为了更好说明本文方法的效果，这里设定了较大比例。分别按照文献[11]和本文的方法对电流进行滤波，结果对比如图2所示。

图2 电流中含有2次谐波时采用文献[11]方法 和本文方法的滤波效果Fig.2 The filtering effect when the current containing second harmonics with the method in literature[11] and the method in this paper

从图2可见，当系统中含有2次谐波等偶数次谐波时，滤波后得到的波形不仅包含直流分量，也包含二次谐波分量。此时计算得到的时间常数为(0.005 4 + j0.000 2)s，出现了虚部，表明该方法在短路电流中含有偶数次谐波电流时失效。相比之下，按照本文提出的方法对原电流进行滤波后得到的结果保持了直流分量的衰减特性，对h(t)取自然对数，计算出的时间常数τ=0.01 s，与设定值一致，说明本文提出的方法适用于短路电流含有各频次谐波的情况。

另外，2种计算方法的计算量的差异主要存在于直流分量的提取过程。从原理上讲，本文提出的方法由于用到了整个周波的数据，因此相比与传统的半波计算方法，计算量约为后者的2倍，并且以加法为主，由于应用于离线分析，因此可以认为本文方法在没有显著提高计算量的前提下提高了时间常数的计算精度。

需注意，在计算等值阻抗过程中虽然用到了三相短路电流的暂态时域仿真结果，但是由于在三相短路过程中短路电流的正弦分量主要以工频为主，因此求出的直流分量保留了工频等值阻抗的信息，求出的等值阻抗也对应于工频等值阻抗。

4 基于电磁暂态短路计算的机电侧系统等值阻抗求取方法

机电-电磁暂态混合仿真中，外部系统往往以戴维南电路进行等值，电磁侧以电流源[12]、功率源[13]或者其改进形式[14]进行等值。一般考虑故障设置在电磁侧，因此戴维南等值电路的阻抗在仿真过程中保持不变，在每次交互过程中，机电侧只需向电磁侧传递戴维南等值电势即可。机电-电磁暂态混合仿真的原理示意图如图3所示。

图3 机电-电磁暂态混合仿真原理示意Fig.3 Principle of electromechanical-electromagnetic transient hybrid simulation

传统的戴维南阻抗求取方法是根据机电暂态数据得到外部系统的节点导纳矩阵，然后在接口处注入单位电流，计算接口处的电压，即为戴维南等值阻抗:

(11)

式(11)中:Req,Leq分别为等值电阻和等值电感;ML为网络节点-端口关联向量;Z为节点阻抗矩阵。

由于机电暂态仿真和电磁暂态仿真在元件建模方面存在差异，这种方法求解出来的等值阻抗只能反映接口在稳态时的特性，而在电磁侧尤其接口处发生故障时，不能充分体现机电侧系统的电磁暂态特性。

本文提出一种基于电磁暂态短路计算的机电侧等值阻抗求取方法。首先，在PSCAD/EMTDC电磁暂态环境下建立机电侧系统的电磁暂态仿真模型，发电机保持“Source”(电压源)的状态。然后分别在接口处设置金属性三相接地短路和经r(r为设定值，但其取值并不会影响外部等值阻抗的求取结果)欧姆电阻三相接地短路，获得短路电流。对2次短路电流进行处理，得到前后2次机电侧等值系统的时间常数，记为τ1和τ2。联立2次时间常数计算公式可得:

(12)

可以得到机电侧系统的等值电阻和等值电感:

(13)

5 仿真验证

在PSCAD/EMTDC中建立如图4所示基于PSCAD+C架构[15]的机电-电磁暂态混合仿真模型，将IEEE39节点系统中的第38号发电机和变压器替换为直流输电线路，直流的逆变侧接入29节点，并选择29母线为接口母线。直流模型参数及控制方式参见CIGRE标准直流模型[16]。发电机采用六阶模型(凸级机)，计及励磁和调速。负荷采用恒阻抗模型。直流系统在电磁暂态侧仿真，交流系统在机电暂态侧仿真。在每个交互周期，机电侧向电磁侧提供戴维南等值电势，电磁侧向机电侧提供正序基波电流相量。机电侧仿真步长设定为10 ms，电磁侧仿真步长设定为50 μs。交互周期设定为10 ms。向量提取算法选用基于全波单相dq变换平均值算法的dq-120算法[17]。分别采用本文方法和传统方法计算29节点外对应的机电侧系统戴维南等值阻抗对比如表2所示。

图4 修改后的IEEE39节点系统Fig.4 The modified IEEE39 system

Ω

由表2可见，由于机电暂态和电磁暂态在建模上存在的元件方面的差异，由传统方法计算出的戴维南等值阻抗的电阻值偏大，所对应系统的时间常数较小，从而影响到故障期间电流的仿真精度。为了进行验证，在直流的逆变侧设置经0.01 Ω三相接地短路故障，故障持续时间为0.1 s。电磁侧仿真结果对比如图5所示。

图5 传统方法求取的戴维南阻抗与本文方法 求取戴维南阻抗的仿真结果对比Fig.5 The comparison of the simulation result between the Thevenin equivalent impedance calculated by the traditional method and the method proposed

由图5(a)中可见，采用本文方法求取的戴维南等值阻抗，当接口处发生三相接地故障时，接口处故障电流直流分量的衰减特性更接近全电磁仿真；由图5(b)可见，与传统方法相比，所仿真得到的电磁侧直流功率也与全电磁仿真更接近，说明采用本文方法求取出的戴维南等值阻抗更能体现外部系统的电磁暂态特性。采用本文提出的方法计算得到的戴维南等值阻抗参数可以显著提升混合仿真故障期间以及故障后的仿真精度。

6 结论

由于机电暂态与电磁暂态存在元件建模上的固有差异，基于机电暂态数据获得的机电侧系统戴维南等值阻抗参数难以体现接口发生故障后机电侧系统的电磁暂态特性，影响到机电-电磁暂态混合仿真精度的进一步提升。本文首先提出一种不受各次谐波影响的外部系统时间常数计算方法，通过在全电磁暂态模型的接口位置设置2次不同接地电阻的三相短路故障，联立时间常数方程计算得到机电侧系统的等值阻抗。仿真结果表明，本文提出的外部系统等值阻抗计算方法可以有效改善机电-电磁暂态混合仿真故障期间和故障后的仿真精度。

[1] 张东辉，冯晓东，孙景强，等. 柔性直流输电应用于南方电网的研究[J]. 南方电网技术, 2011, 05(2): 1-6. ZHANG Donghui, FENG Xiaodong, SUN Jingqiang, et al. Research of VSC HVDC application to China Southern Power Grid[J]. Southern Power System Technology, 2011, 05(2): 1-6.

[2] 周保荣，金小明，吴小辰，等. 特高压直流对交直流并联电网安全稳定影响[J]. 南方电网技术, 2010, 04(2): 31-34. ZHOU Baorong, JIN Xiaoming, WU Xiaochen, et al. Influence of UHVDC system on the security and stability of AC/DC interconnected power grid[J]. Southern Power System Technology, 2010, 04(2): 31-34.

[3] 张建设, 韩伟强, 张 尧, 等. 含±800 kV云广直流的南方电网交直流系统RTDS仿真研究[J]. 南方电网技术, 2009, 03(1): 32-35. ZHANG Jianshe, HAN Weiqiang, ZHANG Yao, et al. RTDS simulation on AC/DC hybrid CSG with the ±800 kV Yun-Guang UHVDC transmission system in operation[J]. Southern Power System Technology, 2009, 03(1): 32-35.

[4] 许爱东，柳勇军，吴小辰. ±800 kV云广特高压直流安全稳定控制策略研究[J]. 南方电网技术, 2008, 02(5): 14-31. XU Aidong, LIU Yongjun, WU Xiaochen. Study on security and stability control strategy for ±800 kV Yun-Guang UHVDC transmission[J]. Southern Power System Technology, 2008, 02(5): 14-31.

[5] 朱鑫要, 汪惟源, 汪成根. 江苏特高压交直流输电交互影响研究[J]. 江苏电机工程, 2016, 35(2):39-42. ZHU Xinyao, WANG Weiyuan, WANG Chenggen. Analysis of interaction between UHVAC and UHVDC for Jiangsu Power Grid[J]. Jiangsu Electrical Engineering, 2016, 35(2):39-42.

[6] HEFFERNAN M D, TURNER K S, ARRILLAGA J, et al. Computation of AC-DC system disturbances part I. interactive coordination of generator and convertor transient models[J]. IEEE Transactions on Power Apparatus & Systems, 1981, 01(11): 15-16.

[7] 岳程燕，田 芳，周孝信，等. 电力系统电磁暂态-机电暂态混合仿真接口原理[J]. 电网技术, 2006, 30(1): 23-27. YUE Chengyan, TIAN Fang, ZHOU Xiaoxin, et al. Principle of interfaces for hybrid simulation of power system electromagnetic-electromechanical transient process[J]. Power System Technology, 2006, 30(1): 23-27.

[8] 柳勇军，梁 旭，闵 勇，等. 电力系统机电暂态和电磁暂态混合仿真程序设计和实现[J]. 电力系统自动化, 2006, 30(12): 53-57. LIU Yongjun, LIANG Xu, MIN Yong, et al. An interface algorithm in power system electromechanical transient and electromagnetic transient hybrid simulation[J]. Automation of Electric Power Systems, 2006, 30(12): 53-57.

[9] 刘文焯，侯俊贤，汤 涌，等. 考虑不对称故障的机电暂态-电磁暂态混合仿真方法[J]. 中国电机工程学报, 2010, 30(13): 8-15. LIU Wenzhuo, HOU Junxian, TANG Yong, et al. Electromechanical transient/electromagnetic transient hybrid simulation method considering asymmetric faults[J]. Proceedings of the CSEE, 2010, 30(13): 8-15.

[10] 李秋硕，张 剑，肖湘宁，等. 基于RTDS的机电电磁暂态混合实时仿真及其在FACTS中的应用[J]. 电工技术学报, 2012, 27(3): 219-226. LI Qiushuo, ZHANG Jian, XIAO Xiangning, et al. Electromechanical-electromagnetic transient rea-time simulation based on RTDS and its application to FACTS[J]. Transactions of CES, 2012, 27(3): 219-226.

[11] 唐宝锋，许庆强，范 辉. 基于数字混合仿真的电网一次时间常数计算方法[J]. 电力系统自动化, 2012, 36(7): 110-115. TANG Baofeng, XU Qingqiang, FAN Hui. A calculating method for primary time constant of power grids based on digital hybrid simulation[J]. Automation of Electric power systems, 2012, 36(7): 110-115.

[12] HUANG Qiuhua, VITTAL Vijay. Application of electromagnetic transient-transient stability hybrid simulation to FIDVR study[J]. IEEE Transactions on Power Systems, 2015: 1-13.

[13] 张树卿，童陆园，郭 琦，等. SMRT交直分网混合实时仿真接口关键技术与实现[J]. 南方电网技术, 2015, 09(1): 39-46. ZHANG Shuqing, TONG Luyuan, GUO Qi, et al. Key techniques and implementation of SMRT hybrid real-time simulation employing AC/DC partitioning scheme[J]. Southern Power System Technology, 2015, 09(1): 39-46.

[14] 杨 洋，肖湘宁，陶 顺，等. 混合仿真电磁侧功率源等效误差原理分析及改进[J]. 电力系统自动化, 2015, 39(24): 104-109.

YANG Yang, XIAO Xiangning, TAO Shun, et al. Electromagnetic side power source equivalent error principle analysis and its improvement for hybrid simulation[J]. Automation of Electric Power Systems, 2015, 39(24): 104-109.

[15] 李 伟，杨 洋，陈鹏伟，等. 电磁-机电暂态混合仿真误差传递机理分析[J]. 南方电网技术, 2015, 09(9): 92-97. LI Wei, YANG Yang, CHEN Pengwei, et al. Analysis on error mechanism for electromagnetic-electromechanical transient hybrid simulation[J]. Southern Power System Technology, 2015, 09(9): 92-97.

[16] 邓广静, 周 威. CIGRE直流输电标准模型的建模及控制策略仿真研究[J]. 电力工程技术, 2009, 28(1):31-34. DENG Guangjing, ZHOU Wei. Study on modeling and control strategy of CIGRE HVDC benchmark system[J]. Electric Power Engineering Technology, 2009, 28(1): 31-34.

[17] 贾旭东，李庚银，赵成勇，等. 基于RTDS/CBuilder的电磁-机电暂态混合实时仿真方法[J]. 电网技术, 2009, 33(11): 33-38. JIA Xudong, LI Gengyin, ZHAO Chengyong, et al. Electromagnetic transient and electromechanical transient hybrid real-time simulation method based on RTDS/CBuilder[J]. Power System Technology, 2009, 33(11): 33-38.

(编辑 徐林菊)

Improved Thevenin Equivalent Impedance Calculating Method for Hybrid Simulation

YANG Yang1, SUN Jing2, YANG Peidong3, XIAO Xiangning4, PAN Mingming5

(1. State Grid Hebei Economic Technology Research Institute，Shijiazhuang 050021, China;2. State Grid Shijiazhuang Power Supply Company, Shijiazhuang 050000, China;3. State Grid Xingtai Power Supply Company, Xingtai 054001, China; 4. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University (NCEPU), Beijing 102206, China;5. China Electric Power Research Institute, Beijing 100192, China)

As the Thevenin equivalent impedance parameter which is deviated form stability-type simulation data can hardly reflect the electromagnetic characteristics of the electromechanical-side system after fault, an improved calculating method of Thevenin equivalent impedance of electromechanical-side system for electromechanical-electromagentic hybrid transient simulation based on electromagnetic transient simulation model is proposed. The Thevenin equivalent impedance parameter is achieved through setting two three phase line to ground faults on the interface bus in the full-electromagnetic transient simulation model and solving the primary time constant equation group in which the primary time constant is based on a calculating method which is not affected by every harmonic component. Compared with the equivalent impedance calculated by the traditional method which calculates the impedance based on the stability-type simulation data and through unit current injection method, the equivalent impedance calculated with the method proposed in this paper can reflect the electromagnetic characteristics more accurately, thus improving the simulation accuracy of electromechanical-electromagnetic hybrid transient simulation during and after fault.

equivalent impedance; primary time constant; electromechanical-electromagnetic; hybrid simulation; accuracy

2017-02-21；

2017-03-31

国家重点研发计划(2016YFB0901102)；中央高校基本科研业务费专项资金资助项目(2015XS22)

TM315

A

2096-3203(2017)04-0036-07

杨 洋

杨 洋(1989—)，男，河北邢台人，工程师，研究方向为电力系统仿真及分析(E-mail：yyang8958@126.com)；

孙 静(1989—)，女，江苏沛县人，工程师，研究方向为电力系统通讯技术及应用(E-mail：413965252@qq.com)；

杨培东(1964—)，男，高级工程师，从事智

能配电网和电力系统运行等方面的工作(E-mail：2471822082@qq.com)；

肖湘宁(1953—)，男，湖南澧县人，博士生导师，研究方向为新能源电网中的电力电子技术及电力系统电能质量等(E-mail：xxn@necpu.edu.cn);

潘明明(1985—), 女, 安徽蚌埠人, 博士生, 研究方向为能源互联网及智能需求响应(E-mail：panmingming@eqri.sgcc.com.cn)。