铝-金刚石界面电子特性与界面肖特基势垒的杂化密度泛函理论HSE06的研究∗

吴孔平 孙昌旭 马文飞 王杰 魏巍 蔡俊 陈昌兆 任斌 桑立雯 廖梅勇‡

1)(安徽理工大学电气与信息工程学院,淮南232001)2)(日本国立材料科学研究所(N IMS),宽带隙半导体研究室,筑波305-0044)

铝-金刚石界面电子特性与界面肖特基势垒的杂化密度泛函理论HSE06的研究∗

吴孔平1)2)†孙昌旭1)马文飞1)王杰1)魏巍1)蔡俊1)陈昌兆1)任斌2)桑立雯2)廖梅勇2)‡

1)(安徽理工大学电气与信息工程学院,淮南232001)2)(日本国立材料科学研究所(N IMS),宽带隙半导体研究室,筑波305-0044)

(2017年1月17日收到;2017年1月25日收到修改稿)

宽带隙半导体金刚石具有突出的电学与热学特性,近年来,基于金刚石的高频大功率器件受到广泛关注,对于金属-金刚石肖特基结而言,具有较高的击穿电压和较小的串联电阻,所以金属-金刚石这种金半结具有非常好的发展前景.本文通过第一性原理方法去研究金属铝-金刚石界面电子特性与肖特基势垒的高度.界面附近原子轨道的投影态密度的计算表明:金属诱导带隙态会在金刚石一侧产生,并且具有典型的局域化特征,同时可以发现电子电荷转移使得FerMi能级在金刚石一侧有所提升.电子电荷在界面的重新分布促使界面形成新的化学键,使得金属铝-氢化金刚石形成稳定的金半结.特别地,我们通过计算平均静电势的方法得到金属铝-氢化金刚石界面的势垒高度为1.03 eV,该值与金属诱导带隙态唯像模型计算的结果非常接近,也与实验值符合得很好.本文的研究可为金属-金刚石肖特基结二极管的研究奠定理论基础,也可为金刚石基金半结大功率器件的研究提供理论参考.

铝-金刚石界面,界面电子态,肖特基势垒,静电势平均

1 引言

由于金刚石具有突出的物理特性,例如宽带隙半导体(约5.47 eV)、高的击穿电场(约10 MV/cm)、高空穴和电子迁移率(µp=2000 cm2·V−1·s−1,µn=1000 cm2·V−1·s−1)和高热导率(22 W·m−1K−1)[1−3],所以被认为是一种典型的、可以用于制备大功率高频高热电子器件的半导体[3].近年来,基于金刚石的高频大功率器件受到广泛关注.对于金属-金刚石肖特基功率器件而言,具有较高的击穿电压(约10 kV)[4,5]和较小的串联电阻(约1Ω)[6],所以金属-金刚石这种金半结在高频高热大功率领域具有非常好的发展前景.然而,金属-金刚石肖特基结也会出现低击穿电场和高反偏电流的情况,主要是由于界面缺陷或者界面态的存在[7,8].因此,金属的选择、低界面态以及金刚石表面激活层的导电性能是影响肖特基势垒高度的重要因素,也是决定金属-金刚石肖特基二极管性能的主要条件.

随着金属-金刚石肖特基功率器件的发展,我们不仅需要知道金刚石与金属接触的设计以及接触引起电学特性的变化,还需要深刻理解金刚石与金属界面电子特性以及肖特基势垒对界面特性的依赖特性.肖特基势垒是界面电子能带偏差导致的结果,而势垒高度的大小主要依赖界面费米(FerMi)能级的位置.近年来,实验上,金属与金刚石界面的结构与电子特性已经被广泛地研究[9−13],而金属铝-金刚石的电子结构与肖特基势垒高度仍然没有统一的结论.尤其对于氢化金刚石表面来说,独特的表面二维空穴气与负电子亲和势备受研究者关注.

在本文中,针对铝与氢表面金刚石形成的金半结开展系统的理论研究,主要内容包括电子特性与界面肖特基势垒,从而确定铝与金刚石形成肖特基的势垒高度.该研究的主要目的是分析金属铝与金刚石界面的微观物理量,通过第一性原理计算得到相关结果并与肖特基唯象模型结果以及实验研究结果进行比较.

2 计算模型和方法

用基于交换关联函数广义梯度近似(GGA)下的密度泛函理论[14]来计算金刚石以及铝-金刚石体系的基态特性,其中使用了Ceperley和A lder[15]交换关联函数.本文中所有计算都由Vienna ab initio simu lation packag(VASP)5.3.3程序代码来完成.用平面波基矢来展开电子波函数,截断能量设定为500 eV,布里渊区K点网格采用Monkhorst-Pack方案自动产生[16],对于金刚石块体网格大小设定为5×5×5,而对于铝-金刚石体系网格大小则设定为9×5×1,结构优化的收敛标准为作用在每一个原子上的Hellmann-Feynman力小于0.01 eV/Å.同时,用准粒子能带结构理论来精确确定金刚石能带位置、离化能以及电子亲和势.带有自能项的准粒子方程与广义孔恩-沈吕九方程将在GW近似下自洽求解,其中零阶GW近似能用空间非局域交换关联函数(Heyd,Scuseria and Ernzerhof,HSE杂化泛函)来表达[17−19],屏蔽函数ω=0.15 a.u.−1[20].本文通过该方法,计算金刚石的带隙结果为5.38 eV,比仅采用GGA方法得到的带隙值(4.1 eV[21])大得多,也更接近金刚石的实验带隙值(5.47 eV).

3 结果与讨论

3.1 表面特性

由于金属铝和金刚石的表面特性可以为研究金属-金刚石界面特性提供明确的参考,所以首先计算金属铝和金刚石的表面特性.对于肖特基势垒高度而言,金属铝和金刚石这种金半结中各组分材料的关键特征参数是金属铝的功函数、金刚石半导体的离化能及其电子亲和势.

3.1.1 金属表面特性

过去使用第一性原理对金属功函数的计算结果都与实验结果符合得非常好[22−24],该方法对金属表面开展的计算具有较好的可靠性.本文计算的金属铝表面由五层金属A l原子层加上15Å厚的真空层构成,这个厚度足够消除周期性重复单元之间的相互作用,确保计算表面结构及其电子特性过程中能量收敛.

金属功函数(ΦM)是与肖特基势垒高度直接相关的重要参数.金属功函数(ΦM)定义为一电子从固体中经过表面逸出到固体外任一点所必须的最小能量:

EF是金属的FerMi能级,Evac是远离金属表面的真空静电势能.通常由两种方法来求得金属功函数(ΦM):第一种方法就是直接利用方程(1),Evac与EF可以直接从金属表面超原胞结构中计算得出,这种方法需要多层金属原子层来建立金属表面超原胞结构,从而消除表面对内部金属原子的影响,此外,对K点数量的选取以及截断能量的大小有一定的依赖;另外一种办法采用宏观平均势的办法[25,26],根据这种方法,金属功函数(ΦM)可以写为

式中,∆E由金属与表面真空静电势能的宏观平均差来确定,∆E金属块体则是由块状金属的FerMi能级与静电势能的宏观平均差来确定,这种方法的优点是几乎不受量子尺寸大小的影响.在本文中,这两种方法都被用来计算金属A l的功函数,并且与已有的理论值[27]与实验值[28]进行比较.金属的功函数由第一种方法计算的结果记为由第二种方法计算的结果记为理论值记为实验值记为数值单位为eV,则计算结果表明:这两种方法的结果非常接近,第二种方法的结果4.11 eV更接近实验值4.26 eV.本文中的金属功函数与肖特基势垒计算中涉及的能量排列均采用第二种方法.

3.1.2 金刚石表面特性

我们采用氢化金刚石表面,其独特的电学特性在上文中已经提及.金刚石表面模型沿着金刚石晶体[100]方向截断所得,并且包含六层C原子层,而表面层上的C原子会产生两个悬挂键,相邻C原子靠近成键,则剩下一个悬挂键由表面H原子饱和,最终达到体系的电中性.优化弛豫即可得到结构稳定的重构后(2×1):H表面,并且金刚石[100]方向上(2×1):H重构的表面已经得到实验[29]或者其他理论计算[30,31]的支持.根据静电势能的宏观平均[25,26],我们不仅可以对表面电子结构进行分析,也可以确定价带顶或者导带底相对真空能级的位置.金刚石表面静电势平面平均与宏观平均如图1所示,根据宏观平均静电势方法,金刚石的离化能IS可以写成

式中∆E金刚石块体是金刚石块体价带顶到宏观平均静电势的距离,∆E则由金刚石与表面真空静电势能的宏观平均差来确定.负电子亲和势(NEA)可以通过离化能与金刚石的带隙值获得.根据图1,氢化金刚石表面的NEA与离化能IS分别为2.54和2.93 eV.这些能量位置与已有的实验[32]和理论[33]都符合较好.

凤尾鱼富含碳水化合物、蛋白质、脂肪、钙、铁、磷、锌、硒等微量元素。锌、硒等微量元素在儿童的智力发育过程中有很重要的作用。研究还发现凤尾鱼中丰富的营养物质能促进人体血液中抗感染淋巴细胞的增加，医学临床实验也证实了凤尾鱼能提高人体在化疗时的耐受力[1]。

图1 (网刊彩色)晶面振荡特性的静电势平面平均分布及其沿着Z(0001)方向上的宏观平均,导带底、价带顶与真空能级也标记在图中Fig.1.(color on line)The p lanar average of electrostatic potential exhibits lattice p lane oscillations,which are fi ltered ou t by Macroscop ic average along Z(0001)d irection,and conduction band MiniMum,valence band top and vacuuMlevel are also Marked.

3.2 界面特性

3.2.1 金属-金刚石界面模型

金属铝-金刚石界面通过超原胞的方法来实现,在上文中我们已经得到结构稳定的金刚石[100]方向上(2×1):H重构的表面,这里我们在该表面的顶部增加了铝原子层构建金属铝-金刚石界面模型.该界面模型由7层碳(C)和四层金属原子层外加18Å厚的真空层所构成.面内晶格常数设定为金刚石的理论平衡值,模拟实验过程中在金刚石表面沉积一层金属.这里我们固定金刚石底部三个原子层,通过能量最小来确定金属铝与金刚石氢化表面之间的间距,也就是在调节金属铝与金刚石氢化表面之间间距的过程中,找到能量最小的确定为最佳间距.一旦间距确定后,z方向([100]方向)固定,面内原子弛豫的办法确定最终的金属铝-金刚石界面模型.

3.2.2 界面稳定性

金属铝-金刚石界面稳定性可以通过单位表面的界面形成能来确定,定义为

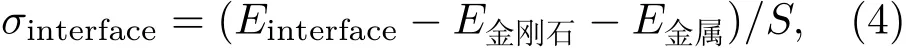
式中Einterface,E金刚石,E金属分别为界面的总能量、金刚石部分的总能量与金属部分的总能量,S是表面的面积,其中金刚石与铝的晶格参数均采用金刚石的理论平衡参数.计算结果为σinterface=−0.03 J/m2,该值小于0,表明金属铝-金刚石界面具有较好的稳定性.

投影态密度(PDOS)与界面电子转移的研究能更清晰地认识界面的电子特性.这里计算界面附近几层原子层的态密度并投影到原子轨道上,能揭示界面成键特性.图2显示了C 2s2p,H 1s和A l 3s3p界面附近的轨道投影态密度,原子层的序号(nL,n=1,2,3,4)从界面处开始算.在图2中,我们很容易发现界面处C 2s2p和H 1s产生了大量的界面带隙态,另外,共振峰揭示界面原子间产生轨道杂化.从图2中可以很清楚地看到:界面附近第一层C原子2p轨道是金属诱导带隙态的主要来源,而氢化表面的H 1s也对金属诱导带隙态提供了少量贡献.除此之外,第二层C受到界面影响已经大大减弱了,对带隙态几乎接近0,第三层C与第四层C原子的态密度已经逐渐恢复到半导体特性.这些也说明金属诱导带隙态在半导体氢化金刚石一侧具有很强的局域化特征.同时,根据FerMi能级的位置,我们也能推测到,有大量电子从金属铝注入到了金刚石表面,使得FerMi能级的位置在金刚石一侧得到了提升.

图2 金属铝-金刚石界面的PDOS图,0点能表示FerMi能级.图中的L表示金属铝-金刚石体系的原子层数,从界面处开始算Fig.2.Pro jected density of states(PDOS)for the A ldiaMond interface.The zero energy corresponds to the FerMi level of the A l-d iaMond interface system.The notation A l/d iaMond-L refers to the L-th A l/diaMond layer starting froMthe interface.

另外,在界面形成后,为了对电子电荷的重新分布有一个详细的描述,同时也能为成键理论提供更多的支撑.界面电子电荷转移可以通过以下方程得到:

式中z是垂直于界面方向的空间坐标位置,ρinterface(z),ρ金刚石(z),ρ金属(z)分别是界面电荷密度的面平均、金刚石外加真空层的电荷密度的面平均以及金属外加真空层的电荷密度的面平均.图3显示了金属铝-金刚石界面的电荷转移情况,在界面处发生了大量的电荷转移,一方面说明电子电荷从金属铝向金刚石一侧转移,这个层分辨投影态密度中FerMi能级的位置是相一致的,另一方面也说明界面处由于电荷的重新分布导致新的键形成,从金属诱导带隙态逐渐消失在金刚石中来看,说明金属与金刚石表面层原子之间存在相互作用;另外图2中A l 3s3p与金刚石表面层C 2p轨道电子投影态密度存在共振特性,说明金属A l电子波函数与金刚石表面C 2p轨道电子之间存在相互作用,并逐渐消失在金刚石内部,使得金属铝与氢化金刚石形成稳定的界面.

图3 (网刊彩色)金属铝-金刚石界面电荷密度差的平面平均(∆ρ(z)),原子的位置在图中用圆圈表示,通过∆ρ(z)对z的积分可以得到电荷转移(q)的大小,图中的竖直虚线表示界面,蓝色表示电荷耗尽,红色则表示电荷积累Fig.3.(color on line)The p lanar average of the induced electron density d iff erence,∆ρ(z),for the A ld iaMond interface.The positions of the atoMs are ind icated by solid circles,and q is the charge transfer calculated by integrating∆ρ(z)over the full z range.The vertical dashed line indicates the interface.

投影态密度与界面电子转移的研究结果表明:从投影态密度的共振峰可以得出,金属铝与金刚石表面在界面处成键,主要是金属铝与C 2p原子轨道杂化;另外,金属铝在氢化金刚石带隙中诱发界面态,这些态仅仅局限在界面附近C原子层中,对于远离界面的C原子而言,这种金属诱发的带隙态逐渐消失,重新恢复为块状金刚石中的C 2p态.

3.2.4 界面肖特基势垒

金属与p型半导体所形成的肖特基势垒高度可以定义为金属FerMi能级与半导体价带顶之间的能量差.界面肖特基的计算涉及两种材料的能带结构的排列,只需要根据沿着垂直界面的z方向上静电势能的变化就可以确定能带的排列.因此,我们做了平行界面的平面平均静电势与电荷转移的分析.而且,为了消除微观原子结构引起的静电势振荡,我们采用了经典电磁理论中的宏观平均方法.金属与p型半导体所形成的肖特基势垒高度可以写成两项和的关系[19]:

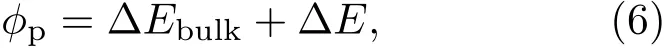
式中,∆Ebulk通常被称为能带结构项,通过对每一种材料的计算来确定能带结构项,用金属的FerMi能级减去金刚石的价带顶;∆E通常被称为排列项,可以通过界面计算时对两种材料的静电势宏观平均做差求得.

根据该方法,我们确定氢化金刚石半导体的导带底(EC)、价带顶(EV),FerMi能级(EF)以及真空能级位置(Evac)如图4所示.最终确定金属铝-氢化金刚石界面肖特基势垒高度为1.03 eV.

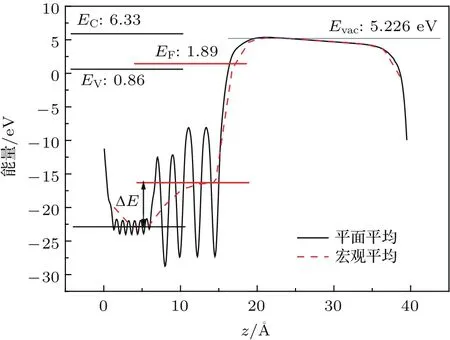
图4 (网刊彩色)晶面振荡特性的平均静电势分布及其沿着z(0001)方向上的宏观平均值,以宏观平均值为参考,铝-金刚石界面的能带位置与FerMi能级也示于图中Fig.4.(color on line)The p lanar electrostatic potential exhibits lattice p lane oscillations,w hich are fi ltered out by Macroscopic average along z(0001)direction.The energy band position and FerMi level of A l-d iaMond interface are shown w ith respect to the Macroscop ic average electrostatic potentials.

令人感兴趣的是将第一性原理的计算结果与目前常用唯象模型的理论计算结果进行比较,唯象模型主要基于材料的一些上文所提及的特征参数.该唯象模型常常被称为金属诱导带隙态模型,该模型基于金属铝诱导界面态,从金属铝过渡到金刚石逐渐衰减,界面处于均匀无缺陷的较为理想化状态,界面相互作用主要是由于金属波函数衰减引起的界面电子重整.然而,肖特基势垒高度主要是由于金属与半导体功函数的差别,而金属-半导体的界面态使得肖特基势垒高度对金属的功函数依赖性变弱,实验上,通过分析不同金属与半导体肖特基势垒高度的变化关系发现,肖特基势垒高度对金属功函数没有直接的依赖性[34],但同时会与金属的电负性相关.这种肖特基势垒高度对金属的功函数依赖性较弱的现象可以通过金属诱导带隙态模型来解释.该模型可以将n型半导体的肖特基势垒高度写成

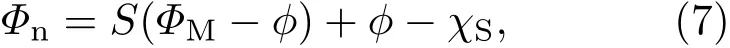
p型半导体的肖特基势垒高度Φp=|Eg−Φn|.(7)式中χS为半导体电子亲和势,S为无量纲钉扎参数,描述金属波函数由界面到半导体内的衰减程度.通常S由经验公式估算得到,估算公式可以写为[35]

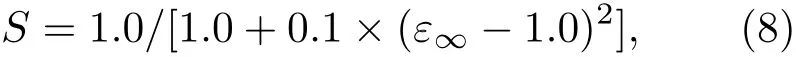
式中ε∞是半导体电介质常数.另外(7)式中ϕ是相对于真空能级的电中性能级位置[36].根据该模型与特征参数,我们得到Φp=0.81 eV.该值小于我们的计算结果1.03 eV,这主要是由于界面不仅仅存在金属诱导带隙态,界面处还形成了新的化学键,而这种化学键的影响并没有包含在该模型中.除此之外,相比唯象模型的计算结果,我们通过第一性原理的计算结果也更符合目前的实验研究结果0.9[37]和1.11 eV[38].

4 结论

本文通过第一性原理计算研究了金属铝-金刚石肖特基结的电子与结构特性,投影态密度表明了金属铝在金刚石表面产生了界面带隙态,并逐渐消失在金刚石内.金属诱导带隙态导致界面电子重整,一定程度上解释了肖特基势垒的主要贡献来自于界面电子重整与界面原子的重构.另外,计算的肖特基势垒高度1.03 eV不仅与近期实验研究结果符合得很好,也比金属诱导带隙态唯象模型的计算结果更准确.界面电子转移过程的微观理解对设计与调控金属-金刚石肖特基结晶体管的功率器件性能具有重要意义,本文通过第一性原理计算研究界面电子特性与肖特基势垒能为金属-金刚石肖特基结晶体管的研究提供理论参考.

[1]W ort C J H,BalMer R S 2008 Mater.Today 11 22

[2]C raw ford K G,Cao L,Qi D C,Tallaire A,LiMiti E,Verona C,W ee A T S,Moran D A J 2016 Appl.Phys.Lett.108 042103

[3]Russell S A O,Sharabi S,Tallaire A,Moran D A J 2012 IEEE Electron Device Lett.33 1471

[4]Volpe P N,Mu ret P,Pernot J,OMnes F,Teraji T,Koide Y,JoMard F,Planson D,Brosselard P,Dheilly N,Vergne B,Scharnholz S 2010 App l.Phys.Lett.97 223501

[5]Huang W,Chow T P,Yang J,Bu tler J E 2004 In t.J.H igh Speed E lectron.Syst.14 872

[6]UMezawa H,K ato Y,Shikata S 2013 Appl.Phys.Express 6 011302

[7]K uMaresan H R,UMezawa H,Shikata S 2010 D iaMond Relat.Mat.19 1324

[8]OhMagari S,Tera ji T,Koide Y 2011 J.Appl.Phys.110 056105

[9]Pereira L,Rod rigues A,GoMes H,Pereira E 2001 D iaMond Relat.Mater.10 615

[10]K awashiMa H,NoguchiH,MatsuMoto T,K ato H,Ogura M,Makino T,Shirai S,Takeuchi D,YaMasaki S 2015 Appl.Phys.Express 8 104103

[11]Makino T,TaniMoto S,Hayashi Y,Kato H,Tokuda N,Ogu ra M,Takeuchi D,OyaMa K,Ohashi H,Okushi H,YaMasaki S 2009 Appl.Phys.Lett.94 262101

[12]Ueda K,KawaMoto K,Asano H 2014 Jpn.J.Appl.Phys.53 853

[13]Tera ji T,Koide Y,Ito T 2009 Phys.Status Solidi(RRL)3 211

[14]Hohenberg P,Kohn W 1964 Phys.Rev.B 136 864

[15]Ceperley D M,A lder B J 1980 Phys.Rev.Lett.45 566

[16]Monkhorst H J,Pack J D 1976 Phys.Rev.B 13 5188

[17]Heyd J,Scuseria G E,Ernzerhof M2006 J.Chem.Phys.124 219906

[18]K rukau A V,Vyd rov O A,IzMaylov A F,Scuseria G E 2006 J.Chem.Phys.125 224106

[19]Paier J,MarsMan M,HumMer K,K resse G,Gerber IC,Ángyán JG 2006 J.Chem.Phys.124 154709

[20]Paier J,MarsMan M,HumMer K,K resse G,Gerber IC,Ángyán J G 2006 J.Chem.Phys.125 249901

[21]Silvestri L,Ladouceu r F 2016 J.Phys.Chem.Lett.7 1534

[22]Meth fessel M,Hennig D,Scheffl er M1992 Phys.Rev.B 46 4816

[23]Fall C J,Binggeli N,Baldereschi A 1999 J.Phys.Condens.Matter 11 2689

[24]Leung T C,Kao C L,Su W S,Feng Y J,Chan C T 2003 Phys.Rev.B 68 195408

[25]Fall C J,Binggeli N,Baldereschi A 1999 J.Phys.Condens.Matter 11 2689

[26]W u K P,Q i J,Peng B,Tang K,Ye J D,Zhu S M,Gu S L 2015 Acta Phys.Sin.64 187304(in Chinese)[吴孔平,齐剑,彭波,汤琨,叶建东,朱顺明,顾书林2015物理学报64 187304]

[27]Singh-Miller N E,Marzari N 2009 Phys.Rev.B 80 235407

[28]Gebreselasie D,Benesh G A 1997 J.Phys.Condens.Matter 9 8359

[29]K awarada H,Sasaki H,Sato A 1995 Phys.Rev.B 52 11351

[30]Hong S,Chou MY 1997 Phys.Rev.B 55 9975

[31]Steckel J A,K resse G,Hafner J 2002 Phys.Rev.B 66 155406

[32]Yu Y,Gu C Z,Xu L F,Zhang S B 2004 Phys.Rev.B 70 125423

[33]van der W eide J,Zhang Z,BauMann P K,W ensellMG,Bernholc J,NeManich R J 1994 Phys.Rev.B 50 5803

[34]Mönch W 2004 Electronic Properties of SeMiconductor In terfaces(Sp ringer Series in Su rface Sciences)(Berlin:Sp ringer)pp147–160

[35]Mönch W 1987 Phys.Rev.Lett.58 1260

[36]K awarada H 1996 Surf.Sci.Rep.26 205

[37]Mönch W 1994 Europhys.Lett.27 479

[38]von W indheiMJ A,Venkatesan V,Malta D M,Das K 1993 J.E lectron.Mater.22 391

(Received 17 January 2017;revised Manuscript received 25 January 2017)

PACS:81.05.ug,73.20.At,73.40.Sx,74.25.F–DOI:10.7498/aps.66.088102

*Pro ject supported by the University Outstanding Talent Cu ltivation PrograMof Anhui Province,China(G rant No.gx fxZD 2016077),the China Postdoctoral Science Foundation(G rant No.2016M601993),and China Scholarship Council(G rant No.201508340047).

†Corresponding author.E-Mail:Wu.Kongping@niMs.go.jp

‡Corresponding au thor.E-Mail:Meiyong.Liao@niMs.go.jp

Interface electronic structu re and the Schottky barrier at A l-d iaMond interface:hyb rid density functional theory HSE06 investigation∗

Wu Kong-Ping1)2)†Sun Chang-Xu1)Ma Wen-Fei1)Wang Jie1)WeiWei1)Cai Jun1)Chen Chang-Zhao1)Ren Bin2)Sang Li-Wen2)Liao Mei-Yong2)‡

1)(School of Electrical and InforMation Engineering,Anhui University of Science and Technology,Huainan 232001,China)2)(W ide Band-Gap SeMi-Conductor Research Group National Institu te for Materials Science(NIMS),Tsukub 305-0044,Japan)

Diamond is regarded as one of themost p roMising seMiconductormaterials used for high power devices because of its superior physical and electrical properties,such as w ide bandgap,high breakdown electric field,high Mobility,and high thermal conductivity.Highpower diamond devices are now receivingmuch attention.In particular,Schottky diode based on aMetal/diaMond junction has p roMising app lications,and high breakdown voltage has been achieved,though un fortunately its forward resistance is high.In this paper,the fi rst princip les calculations are perforMed to study the electronic structure of interface and the Schottky barrier height of A l-diamond interface.The projection of the density of states on the atoMic orbitals of the interface atoMs reveals that the typical A l-induced gap states are associated w ith a sMooth density of states in the bu lk diaMond band gap region,and these gap states are found to be localized w ithin three atoMlayers.At the same time,electronic charge transfer makes the FerMi level upgrade on the side of diamond.Besides,the typical A l-induced gap stateModel gives a siMp le picture about what deterMines Schottky barrier height at A l-diamond interface,by assuMing an ideal,defect-free and laterally hoMogeneous Schottky interface in which the only interaction comes froMthe decay of the electron wave function froMthemetal into the seMiconductor,which in turn induces electronic charges to be rearranged in the region close to the interface.As for the electronic charge transfer,this potential shift can be extracted by subtracting the superiMposed p lanar or Macroscopically averaged electrostatic potentials of the A l and diamond surfaces(at frozen atoMic positions),froMthe p lanar or macroscopically averaged potential of the relaxed A l-diaMond interface.The electronic charge transfer suggests that the forMation of an interface should be associated w ith the formation of new cheMical bonds and substantial rearrangements of the electron charge density.Especially,we obtain the Schottky barrier height of 1.03 by the fi rst princip le,which is in good agreeMent w ith the results froMphenoMenologicalModel and experiMent.The research resu lts in this paper can p rovide a theoretical basis for the research of themetal diamond Schottky junction diode,and can also give a theoretical reference for the research of theMetal-seMiconductor highpower device based on diaMond Material.

A l-diamond interface,interfacial electronic state,Schottky barrier,electrostatic potential average

10.7498/aps.66.088102

∗安徽省高校优秀拔尖人才培育资助项目(批准号:gx fxZD 2016077)、中国博士后科学基金(批准号:2016M601993)和中国国家留学基金委项目(批准号:201508340047)资助的课题.

†通信作者.E-Mail:W u.Kongp ing@niMs.go.jp

‡通信作者.E-Mail:Meiyong.Liao@niMs.go.jp

©2017中国物理学会C h inese P hysica l Society

http://w u lixb.iphy.ac.cn