电缸非线性位置误差研究*

杨继东， 赵叶轮， 万彪刚， 胡 敏

(重庆大学 机械工程学院,重庆 400044)



电缸非线性位置误差研究*

杨继东， 赵叶轮， 万彪刚， 胡 敏

(重庆大学 机械工程学院,重庆 400044)

针对电缸直线运动位置误差进行了研究，提出了一种“最小二乘法线性拟合补偿、非线性自适应模糊比例—积分—微分(PID)非线性误差补偿”的复合模式误差补偿方法，重点分析了非线性误差的补偿，建立了电缸测试系统的数学模型并进行了仿真，验证了自适应模糊PID进行补偿的可靠性；结合实验进行了验证，证明了该方法具有很好的可行性,取得了理想的效果。

位置误差； 电缸测试； 模糊比例—积分—微分(PID)； 误差补偿

0 引 言

系统误差来源，主要分为机械误差和控制误差。在机械结构已经固定的情况下如何提高精度是一个很重要的问题，而进行误差补偿被证明是提高和改善整个系统的精度、性能的一个非常重要的手段。针对位置误差补偿，郭亮等人提出了一种基于半闭环控制下的间隙补偿算法，进行了反向间隙的补偿[1]；沈云波等人提出了一种神经网络误差补偿技术，对数控机床的空间位置进行了补偿[2]；朱赤洲提出了一种基于数控系统插补数据的空间误差补偿方法，并在数控机床上进行了应用[3]。

上述文献大多数对多轴数控机床的空间误差进行研究，本文针对直线电缸的误差补偿，提出了一种复合模式进行误差补偿的方法，在电动缸参数测量领域以及直线位移误差补偿方面均具有一定的意义和参考价值。

1 线性误差补偿

线性误差补偿，一般可以采用最小二乘线性拟合的方法。张开远等人利用最小二乘法对pH 值传感器温度进行了建模补偿，取得了理想的效果[4]。该方法只需计算出线性比例的系数，便可采用修正脉冲当量的方法进行相应的补偿。

记si为第i个目标点位，xi为点位偏差，1≤i≤n,则最小二乘线性拟合的方程为

(1)

经过脉冲当量与指令位移之间的转换关系可得

δ′=(1+k)δ

(2)

式中 k为线性误差平均比例系数;δ为系统修正前脉冲当量;δ′为系统修正后脉冲当量。

2 非线性误差补偿

一般补偿非线性误差有硬件补偿和软件补偿两种方法，鉴于硬件补偿增加了成本且电路复杂[5]，本文提出了一种非线性自适应模糊PID的软件补偿方法对系统模型的非线性误差进行补偿。

2.1 电缸测试系统模型

测试系统采用DMC5480运动控制卡与IPC相结合的硬件组合方式来控制伺服电机，通过磁栅尺将工作台的位置信息反馈给上位机，形成一个全闭环伺服控制系统。系统结构如图1所示。

图1 电缸测试伺服系统

建立电缸测试系统模糊PID控制框图如图2所示。其中，e和ec分别为偏差和偏差变化率。

图2 电缸测试系统模糊PID控制框图

2.2 电缸测试系统数学模型与仿真模型建立

电缸测试系统结构中，IPC通过运动控制卡将指令位移转换为角位移，可将运动控制卡等效为一个比例环节，比例系数为K1；机械传动结构为同步带传动将角位移转换为直线位移等效为比例环节，比例系数为K2；驱动装置可以近似等效为惯性环节，结合伺服电机的传递函数模型，建立整个系统的数学模型。

伺服电机为典型非线性的复杂被控对象，不考虑电机的磁路饱和并忽略带负载时电枢反应的影响，令粘滞摩擦系数B=0，则伺服电机的传递函数为

(3)

式中 KT为转矩系数；Ra为电枢电阻；La为电枢电感；J为转动惯量。

将驱动器等效为惯性环节，其传递函数为

(4)

式中 KV为比例增益；TV为积分时间常数。

根据实际测试选用的伺服电机，将各参数分别代入式(3)、式(4)得到

(5)

(6)

根据建立的数学模型，利用Matlab/Simulink进行建模仿真，如图3、图4所示。

图3 模糊PID控制框图

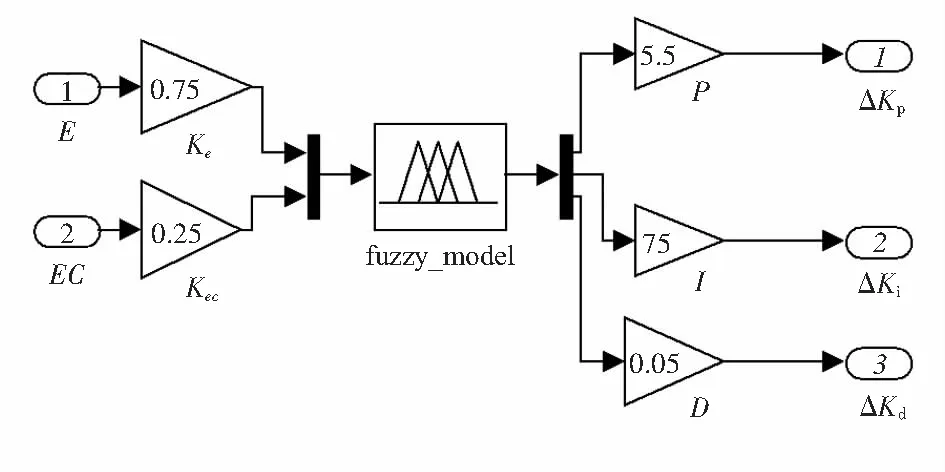
图4 模糊子系统控制框图

2.3 模糊PID控制器的仿真结果

初始PID参数经过手动调试取Kp0=15，Ki0=25，Kd0=0.5；根据实际测试速度跟随误差为-20～28 mm/s，位移跟随误差为-8～8 mm，模糊控制器各输入参数E，EC以及输出参数ΔKp,ΔKi,ΔKd的论域均取{-6,6}，隶属度函数左右两侧选取高斯基函数、中间取三角形函数，则模糊控制器输入输出比例调整系数分别取为Ke=0.75，Kec=0.25，P=5.5，I=75，D=0.05。在阶跃信号下，利用Matlab/Simulink进行仿真，响应曲线如图5所示。

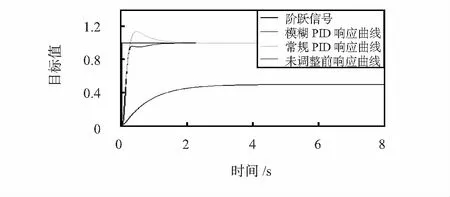
图5 电缸测试系统阶跃响应曲线

由仿真结果可知：电缸测试系统在进行调整前调整响应时间为5.8 s，无超调，稳态误差为50 %；常规PID调节调整响应时间为2.8 s，超调量为14 %，无稳态误差；自适应模糊PID调节调整响应时间为1.4 s，无超调和稳态误差。

经过自适应模糊PID的调节之后，电缸测试系统的动态性能和稳态性能都得到了极大的提升，极大地减小系统带来的非线性误差。

3 电缸测试实验结果

同步带的带轮直径为35 mm，测试的电缸最长的行程达1 m，每0.1 m作为一个间隔点位进行测量，各点位测量多次然后取平均值，正、反行程分别测量一次。

表1 误差补偿前后精度对比 mm

由表1可以看出:通过最小二乘法线性拟合补偿、自适应模糊PID非线性补偿，正向定位精度、负向定位精度、双向定位精度、双向重复定位精度分别降到了原来的2.59 %，1.43 %，2.49 %，23.89 %，补偿后双向重复定位精度在0.05 mm以内，总的定位精度得到了极大的提高，达到了预期的目标，能够满足工业应用的要求。

4 结 论

提出的系统中，利用线性拟合的方法能够很大程度减少电缸的线性误差，而且简单可行；提出了一种非线性自适应模糊PID控制器的控制方法，通过仿真结果说明其具有很好的鲁棒性和自适应能力，能够极大减小非线性误差。通过实验，应用本文所提的复合模式进行误差补偿后电缸测试系统精度得到了极大的提高，证明了文中提出的复合模式误差补偿方法在实际应用中具有可行性以及良好的有效性，可为其他行业的误差补偿提供一定的参考。

[1] 郭 亮,张东升,陶 涛．基于半闭环控制的数控系统反向间隙补偿[J]．组合机床与自动化加工技术,2011，4：47-50．

[2] 沈云波，童景琳．数控机床空间位置误差的检测及神经网络误差补偿技术[J]．工具技术,2006(4)：69-72．

[3] 朱赤洲．数控机床三维空间误差建模及补偿技术研究[D]．南京：南京航空航天大学,2012．

[4] 张开远，周孟然，闫鹏程，等. 基于最小二乘法的 pH 值温度补偿系统设计[J].传感器与微系统，2015，34(5):109-111,122.

[5] 江 东，单 薏，刘绪坤，等．函数拟合法力数字传感器的非线性和温度补偿[J]．传感器与微系统,2016,35(2)：16-18，22．

[6] 杨继东，刘 昆，杨中山，等.电动缸性能参数测试系统设计[J].重庆大学学报，2015,38(4)：31-37.

[7] 张 虎,周云飞,唐小琦,等．数控机床空间误差的无模测量与补偿[J]．华中科技大学学报,2002,30(1)：74-77．

[8] 何振亚．数控机床三维空间误差建模及补偿研究[D]．杭州：浙江大学,2010．

[9] 杨中山．基于IPC的电动缸实验平台测控系统设计[D]．重庆：重庆大学,2014．

Research of nonlinear position error of electric cylinder*

YANG Ji-dong, ZHAO Ye-lun,WAN Biao-gang, HU Min

(College of Mechanical Engineering,Chongqing University,Chongqing 400044,China)

Aiming at position error of linear motion of a type of electric cylinder,a composite patterns error compensation method of “least squares linear fitting compensation,nonlinear adaptive fuzzy PID of nonlinear error compensation”is proposed,specially analyze on nonlinear error compensation and mathematical model for electric cylinder test system is established and simulated to prove the reliability of the adaptive fuzzy PID compensation.It is combined with the experiment to verify and it is proved that the method is feasible and ideal effect is obtained.

position error; test of electric cylinder; fuzzy proportion integration differentiation(PID); error compensation

10.13873/J.1000—9787(2017)07—0073—02

2016—07—16

国家自然科学基金资助项目(51375507)

TP 391

A

1000—9787(2017)07—0073—02

杨继东(1966-)，男，通讯作者，博士，副教授，从事机电一体化技术、智能制造及装备研究工作，E—mail：yjd311910@126.com。