基于叠层衍射成像的二元光学元件检测研究∗

王磊 窦健泰 马骏†袁操今 高志山 魏聪 张天宇

1)(南京理工大学电子工程与光电技术学院,南京 210094)2)(南京师范大学物理科学与技术学院,南京 210097)

基于叠层衍射成像的二元光学元件检测研究∗

王磊1)窦健泰1)马骏1)†袁操今2)高志山1)魏聪1)张天宇1)

1)(南京理工大学电子工程与光电技术学院,南京 210094)2)(南京师范大学物理科学与技术学院,南京 210097)

(2016年11月8日收到;2016年12月30日收到修改稿)

本文提出了一种基于叠层衍射成像(ptychography)的二元光学元件的检测方法,该方法可实现对二元光学元件表面微观轮廓的检测以及特征尺寸的标定.相比于传统的二元光学元件检测方法,其使用无透镜成像技术,简化了系统结构并可适用于特殊环境下的检测.该方法可直接通过采集多幅衍射图,利用叠层衍射成像迭代算法可精确地复原大尺寸待测元件的表面微观轮廓,提高大尺寸器件的检测效率.本文模拟仿真了台阶高度与噪声大小对纯相位台阶板复原结果的影响,并在光学实验中选取计算全息板为样品,复原样品的表面微观轮廓信息以及得到台阶高度.以白光干涉仪检测结果为标准,该方法在精度要求不太高的前提下,可获得令人满意的成像质量.

叠层衍射成像,二元光学元件,相位复原,特征尺寸标定

1 引 言

随着衍射光学技术的发展和加工技术能力的提高,二元光学元件越来越普遍地应用于现代光学系统中.二元光学元件的工作原理是依据光的衍射理论,利用光学透镜表面的三维浮雕结构对光的相位进行调制、变换来满足应用需求.与以光的折射和反射原理为基础的光学元件相比,二元光学元件具有质轻体薄、设计灵活并且对入射光波可以自由调制等特点［1].通过折衍混合的方式,可以在提高光学系统成像质量的同时简化系统结构,减轻重量.常用的二元光学元件检测方法大致可分为干涉法与非干涉法,干涉法包括白光干涉［2]、数字全息显微［3]等,非干涉法有偏振检测法［4]及其他检测方法.白光干涉检测精度高,但仪器操作复杂,单次测量范围小,难以实现较大范围待测件的检测.偏振方法,如穆勒矩阵检测手段可以实现纳米量级的结构测量,但实验系统结构复杂.由于检测时不是可见即所得,因此需要先对光学元件的光学特性建模,然后将测得的数据与数据库中的数据匹配,实现特征参数标定.由于二元光学元件的折射率、三维形貌及内部结构等都可直接改变透射或反射光场的相位分布,光束的相位分布往往包含比强度分布更多的物体结构信息,因此可以通过相位恢复技术实现对二元光学元件的检测.叠层衍射成像技术(ptychography)作为一种新兴的无透镜成像技术,在保证照明光与样品有一定重叠率的基础上,通过采集阵列扫描的衍射图样信息,经相位恢复迭代算法处理后能够很好地恢复样品的复振幅信息［5−7].1969年,Hoppe［8]首先提出相干衍射成像,后经Fienup［9]的改进而逐步发展起来.自Fienup算法提出以来,在相当长时间内没有长足的发展,对很多样品都会出现收敛速度慢或者不收敛的情况.直到2004年,Rodenburg和Faulkner［10]结合叠层衍射成像方法和迭代算法提出了一种基于横向扫描的数据记录和重建方法——叠层衍射迭代(ptychographic iterative engine,PIE)算法,而Maiden和Rodenburg［11]在PIE基础上对探针位置迭代更新提出改进型叠层衍射迭代(extended ptychographic iterative engine,ePIE)算法.改进后的算法不仅可以同时重建探针和样品的复振幅信息,而且重建后得到的结果也具有更好的信噪比［12].叠层衍射成像具有非透镜成像技术如全息技术的共同优点,对相位比较敏感、非接触成像且成像质量理论上能达到衍射极限的分辨率.但相比于全息技术,叠层衍射成像技术摆脱了参考光束的束缚,系统结构更为简单,复原结果排除了共轭像的干扰［13].

基于叠层衍射成像的诸多优点,叠层衍射成像技术已广泛应用于X射线成像［14]、生物医学成像［15]以及光学图像加密［16]和光学元件检测［17−20]等领域.国内外对叠层衍射成像技术在光学测量以及光学元件检测方面的应用做了许多研究.Wang等［17]设计了两块旋转衍射光学元件用于控制叠层衍射成像的入射光场获取准确的探针信息,提高了成像质量并且可用于大视场的范围成像.Claus等［18]使用双波长叠层成像技术,实现了待测样品的表面微观轮廓检测.Tao等［19]结合叠层衍射成像通过已知分布的相位板调制光场,利用相干调制成像方法复原得出复杂光学元件的透过率函数.Wang等［20]将大孔径光学元件的透射波前作为照明光入射到被扫描物体上,利用ePIE技术恢复照明光,实现了对大口径连续分布相位板的测量.这些研究为光学测量与光学元件的检测提供了新思路.二元光学元件的特征与优点源于其表面三维浮雕结构,而其对光场相位的调制作用是能通过相位恢复技术检测的理论基础.本文根据叠层衍射成像技术可实现样品复振幅的复原、实验系统结构简单以及成像范围大等特点,提出一种新的二元光学元件检测方法.检测系统通过简单变化叠层衍射成像光路的光阑尺寸与透镜位置,获得满足检测需求的合适的扫描照明光.采用ePIE算法对采集的衍射图样进行复原处理,实现了二元光学元件的表面微观轮廓检测与特征尺寸标定.为验证检测方法的可靠性,分别进行了仿真实验与光学实验:仿真实验验证了复原算法的可行性,分析了台阶高度范围及噪声对检测结果的影响;光学实验对待测样品的表面微观轮廓进行复原并对样品的台阶高度做出标定.

2 理论分析

2.1成像原理

叠层衍射成像通过记录照明光相对于样品在垂直于光轴的平面上移动形成的衍射光强分布,然后采用PIE或ePIE算法对采集的衍射图样进行处理后可以得出原始样品的复振幅信息.叠层衍射成像技术成功的关键在于相邻扫描位置之间有一定的重叠率［21],重叠的部分是对样品不同区域处的相位信息进行锁定.使用探测器记录叠层的衍射图样信息,生成大量的数据冗余,利用鲁棒的相位恢复迭代ePIE算法能够很好地恢复样品和照明探针的复振幅信息［22].二元光学元件由于其表面的微观三维轮廓结构会对照明光场产生调制作用,利用这一特征通过叠层衍射成像方法可以复原二元光学元件的相位信息,而获得的相位信息可用来检测待测元件的表面微观轮廓结构［23].在照明光透射式作用于二元光学元件时,假设二元光学元件是由同种材料构成,折射率为n0,表面微观轮廓结构函数为T(r),其中r表示r(x,y)为物平面笛卡尔坐标系,对应透射率函数的相位为Δφ(r),则有如下关系:

λ为照明光波长.这表明在没有考虑累加2π的整数倍的相位差(包裹相位)时,元件表面的垂直高度的检测范围大小为一个波长,若要完全复原样品需完成相位解包裹.本文提出的方法就是基于叠层衍射成像复原二元光学元件的相位函数,再通过待测元件的相位函数得到其表面微观轮廓结构.

2.2检测方法的结构与算法流程

Rodenburg和Faulkner［10]提出基础的叠层衍射成像光路中采用的照明光是近似平行光,但对于衍射光学元件的表面微观轮廓结构的检测,往往会出现细节信息无法恢复的问题.一方面由于元件衍射作用导致采集的衍射斑光强分布对比度过大,比如一些区域已经过曝而另外的一些区域光强却过小,造成无法准确完整地记录照明光经衍射光学元件调制后的变化信息;另一方面,采用平行光照明的方式存在无法充分利用电荷耦合器件(CCD)靶面的缺陷,检测较小尺寸元件时,衍射图样集中在较小区域,包含待测物的复振幅高频信息的不足会出现细节信息缺失的情况.本文实验光路原理如图1所示,对基础的叠层衍射成像光路上做一些改进,在小孔光阑的后面放置一块透镜用来生成发散的球面波照明光［18].这样可以通过调节光阑的大小或者改变透镜到待测件的距离获得合适的照明光场,在充分利用CCD靶面尺寸的基础上避免出现衍射斑对比度过大的问题,而且改变透镜与待测件之间的距离可以实现不同尺寸元件的检测.

图1 (网刊彩色)加透镜改进的叠层衍射成像光路图Fig.1.(color online)The optical system of ptychographic.

本文中使用ePIE算法处理数据,详细的算法［24]步骤如下.

步骤1设物体为O(r),到达物表面照明光为P(r),其中r(x,y)为物平面笛卡尔坐标系.照明光探针阵列扫描步长为Rj=(Rx,j,Ry,j)(j=1,2,3,...,J),其中j为照明光对待测物相对位移的次数.首先赋予待测样品一个初始的随机猜测On(r)以及根据小孔光阑尺寸大小估算猜测的照明光为Pn(r),其中n表示迭代次数.

步骤2照明光经待测样品后出射的透射光场复振幅分布为

其中Pn(r−R(j))表示照明光与待测物相对位移后的复振幅分布.

步骤3将出射的透射光场复振幅传输到CCD面,在CCD面将获得对应的衍射光强分布.这里假设是菲涅耳衍射传输,则有

其中Fr表示菲涅耳衍射变换,u表示CCD面的坐标系.ψn(u,R(j))可以表示为

其中|ψn(u,R(j))|表示振幅分布,θn(u,R(j))表示相位分布.

步骤4用CCD实际采集到的衍射光强替换变换得到的复振幅分布的振幅,保持相位部分不变,即

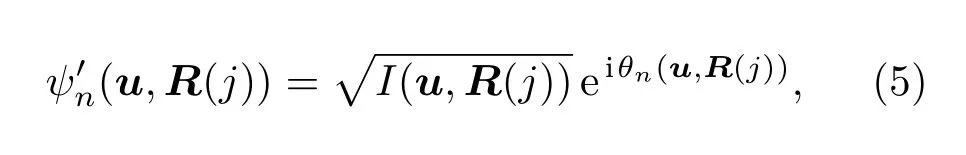
其中I(u,R(j))表示CCD实际采集到的强度分布.

步骤5将更新后的衍射光场分布逆传输回待测物面,

其中Fr−1表示逆菲涅耳衍射传输变换.

步骤6用做强度限制后的透射光场复振幅分布分别更新物函数和照明光场,更新函数如下:

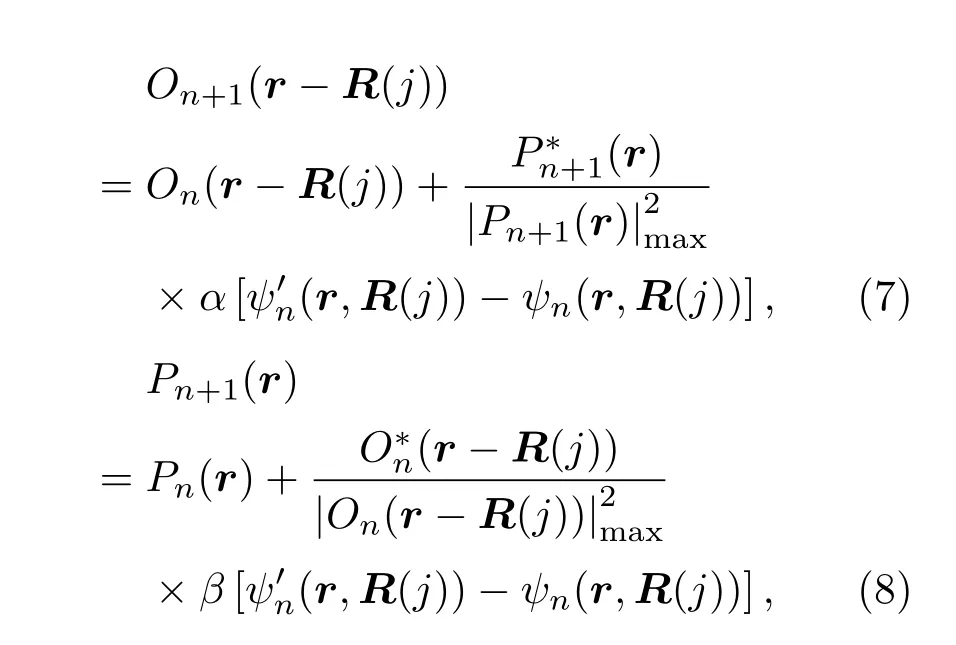
步骤7在保证重叠率的基础上(一般大于70%),移动照明光场重复上述步骤2—6直至准确地收敛出待测物体的振幅与相位信息.

步骤8通过前面所述(1)式的相位与物体表面的微观结构关系可以计算得到的待测物体的表面微观轮廓.

具体的算法流程如图2所示.

图2 ePIE算法流程图Fig.2.Flow chart diagram of ePIE algorithm.

图3 (网刊彩色)(a)样品原图;(b)复原结果图;(c)样品原横截面曲线(黑色横线处);(d)复原横截面曲线Fig.3.(color online)(a)Sample for simulation;(b)reconstruction of the sample;(c)cross-section of sample(indicated by black line in sample);(d)reconstruction of the cross-section.

3 仿真实验与分析

3.1台阶高度复原算法验证

仿真样品选取的纯相位型台阶板如图3(a)所示,图3(c)是其黑色横线处的横截面曲线.仿真的工作波长λ为632.8 nm,平行光经直径约2 mm的不规则光阑遮挡后,传输20 mm到焦距为30 mm的透镜前表面.透镜后表面距待测物面55 mm,CCD面放置在物后80 mm处.对于待测物面的采样点数选取为400 pixels×400 pixels,像元大小为6µm,扫描方式是7×7阵列扫描.扫描步进为20 pixels,保证相邻位置的重叠率大于90%,最终复原出的有效像素数为321 pixels×321 pixels.图3(a)中样品的台阶高度为0.7λ,经过ePIE算法迭代300次后复原的结果如图3(b)和图3(d)所示.复原结果表明,除了算法本身带来的噪声外,叠层衍射成像通过ePIE算法能准确复原出台阶板表面的微观结构.

3.2台阶高度对复原结果的影响

为了更好地展示本文所提方法对台阶高度的复原,分析了不同台阶高度对复原结果的影响.选取台阶高度从0.1λ到1.9λ,间隔为0.2λ的10个不同台阶高度的样品,其他仿真条件不变,完成上面的实验得到对应的复原结果.为了对复原结果与原样品进行比较,引入均方差(MSE)作为复原的台阶高度的误差评定,并定义

其中,样品O(x)和复原结果O′(x)分别为图3(c)和图3(d)所示的横截面处的高度数值变化函数;x为对应的位置横坐标.将复原结果每个波长的台阶高度选取10个横截面数据为一组,同一组获得的MSE再做均值处理,获得不同台阶高度复原结果精度的误差变化曲线,如图4(a)所示.由图4(a)曲线可以看出:随着台阶高度的增加,复原结果的误差值也会增加;台阶高度小于1.5λ时复原结果的MSE误差较小,MSE稳定在0.1以下,但在台阶高度大于1λ后有较大的变化;MSE误差在台阶高度大于1.5λ情况下会陡然增加,这时的复原结果难以精确标定原样品的表面微观轮廓,表明已超出叠层衍射成像可检测的最大台阶高度范围.这与Hüe等［22]提出的ePIE算法可恢复的相位范围相符合,但由于台阶样品高度的变化幅度较大,带来的相位跃变也较大,因此可恢复的相位范围会进一步减小.

由于MSE不能准确地标定检测的特征尺寸即台阶高度结果的相对精确度,为此将获得的每个台阶数据取均值进行处理,再同原样品的台阶高度相比较,引入相对误差σ,

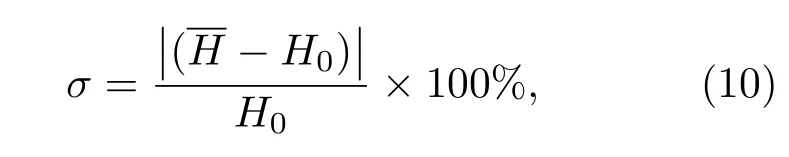
图4 (a)不同台阶高度样品复原MSE误差;(b)不同台阶高度样品复原相对误差Fig.4.(a)Reconstruction error MSE of the di ff erent step height samples;(b)reconstruction relative error δ of the di ff erent step height samples.

由上述分析可得出,由于衍射元件的相位变化不是渐变的,比如本文中所用的纯相位台阶板样品,阶跃的相位变化会影响叠层衍射成像复原样品结果的精度.这是因为叠层衍射成像技术是利用相邻重叠区域的相位解收敛复原出样品的复振幅,突变过大的阶跃相位会导致相位收敛出现问题;当样品的台阶高度超过1个λ即相位变化超过2π,就要对最后的复原结果进行相位解包裹处理,而突变太大的相位在解包裹时会出现歧义解.分析仿真结果可知,叠层衍射成像的检测衍射光学元件的表面微观轮廓结构最大高度不超过1.5λ.

3.3噪声对台阶高度复原结果的影响

叠层衍射成像使用的ePIE算法对噪声具有一定的鲁棒性,对于传统样品如生物标本等在一定的噪声影响下依然能够复原出清晰的高质量图像.由于相位型台阶板等衍射光学元件有相位突变的特征,采集衍射图样时,探测器带来的噪声大小对最终复原结果有很大的影响.保持其他仿真条件不变,对0.7λ台阶高度的样品采集的衍射图样加入1%—10%的随机噪声,算法迭代300次后按照(9)式得出横截面的MSE,变化趋势如图5(a)所示.从变化趋势可以看出,随着加入的随机噪声的增加,MSE值逐渐增大,复原结果的质量逐渐下降.加入的随机噪声在5%以内复原结果的MSE值低于0.02;当加入的随机噪声超出5%时依然能复原出样品的像,图5(b)为7%随机噪声的复原结果,但成像质量较差且噪声带来的细节干扰对样品的特征尺寸标定带来困难.在实际实验中用于采集衍射图样的CCD会带来噪声,实验结果表明实际光学实验成像检测时选择合适的CCD以及正确抑制噪声能明显提高最终的复原结果的质量.

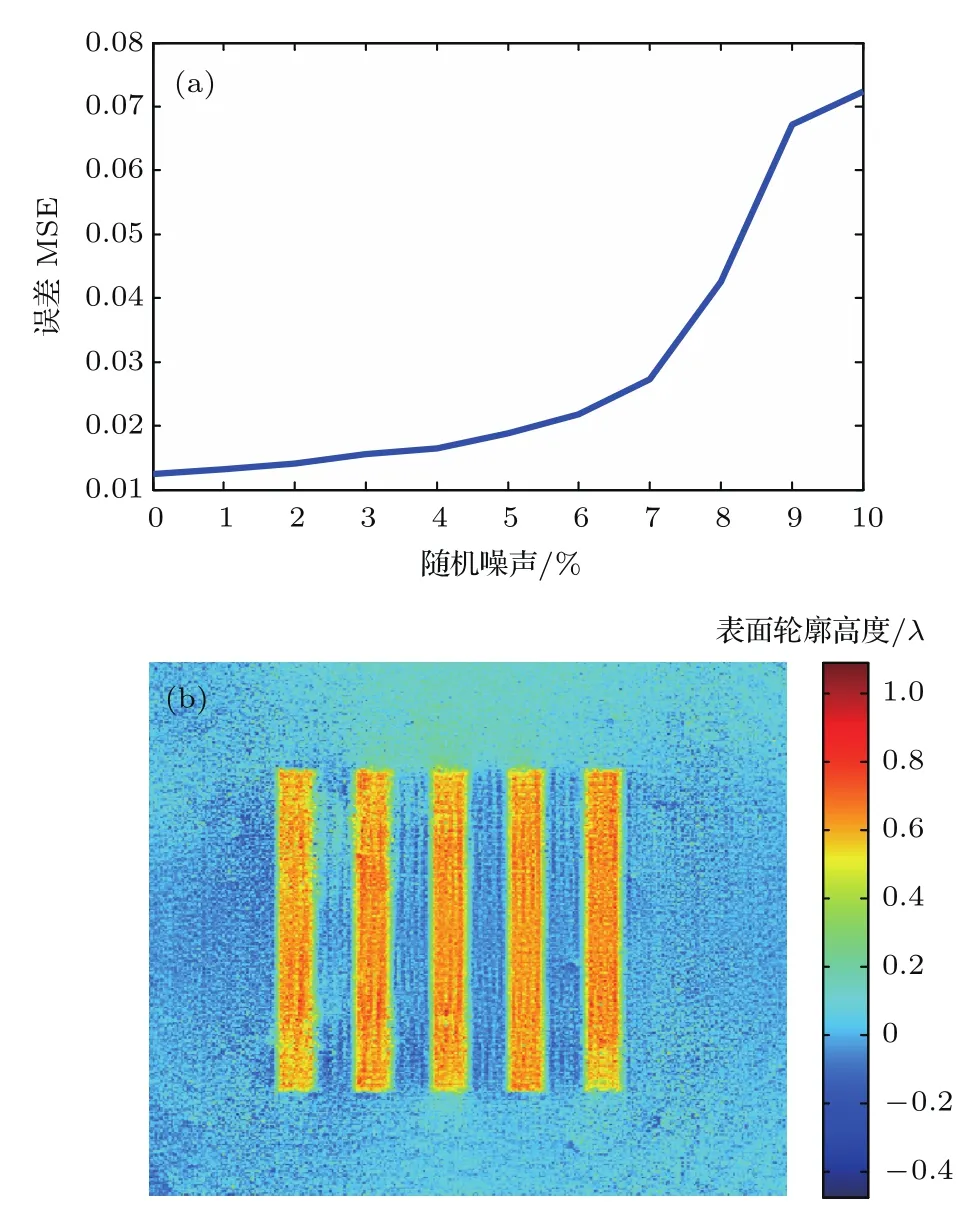
图5 (网刊彩色)(a)不同随机噪声样品复原MSE误差;(b)加7%随机噪声样品复原结果Fig.5.(color online)(a)Reconstruction error MSE of the samples by adding di ff erent random noises;(b)recovered result of the sample by adding 7%random noise.

4 实验结果与分析

基于仿真实验的结果,搭建了一套用于检测衍射光学元件的叠层衍射成像系统.实验装置按图1所示的光路搭建,激光光源采用波长为632.8 nm的氦氖激光器.激光光束经扩束准直后成平面波,再依次通过可变的小孔光阑和透镜后到达样品面,最后由CCD采集衍射图样.通过改变光阑大小和透镜到样品的距离可以获得合适的照明光,光阑直径为d,透镜的焦距f=30 mm,保持透镜紧靠在光阑后距离L1=15 mm.若样品放在透镜后距离为L2处,则可估算得出对应照明光尺寸,直径为D=d(L2−f)/f.二维阵列扫描是由两个精度为0.8µm的电动位移台组合实现的,接收衍射图样的CCD的像元尺寸为4.4µm,分辨率为1600 pixels×1200 pixels.实验选择计算全息板(computer-generated holography,CGH)作为样品,完成表面微观轮廓检测和特征尺寸台阶高度的标定.

4.1二元光学元件的表面微观轮廓检测

为了检测较大尺寸的二元光学元件,对应的照明光的尺寸要求较大.实验中小孔光阑的直径为2 mm,透镜到样品的距离为60 mm,估算的照明光直径约为2 mm,CCD放置在CGH后80 mm处.控制电动平移台完成对样品7×7阵列扫描,扫描步进为0.15 mm,重叠率为92.5%.采集的衍射图样经ePIE算法300次迭代后复原出的结果如图6所示.

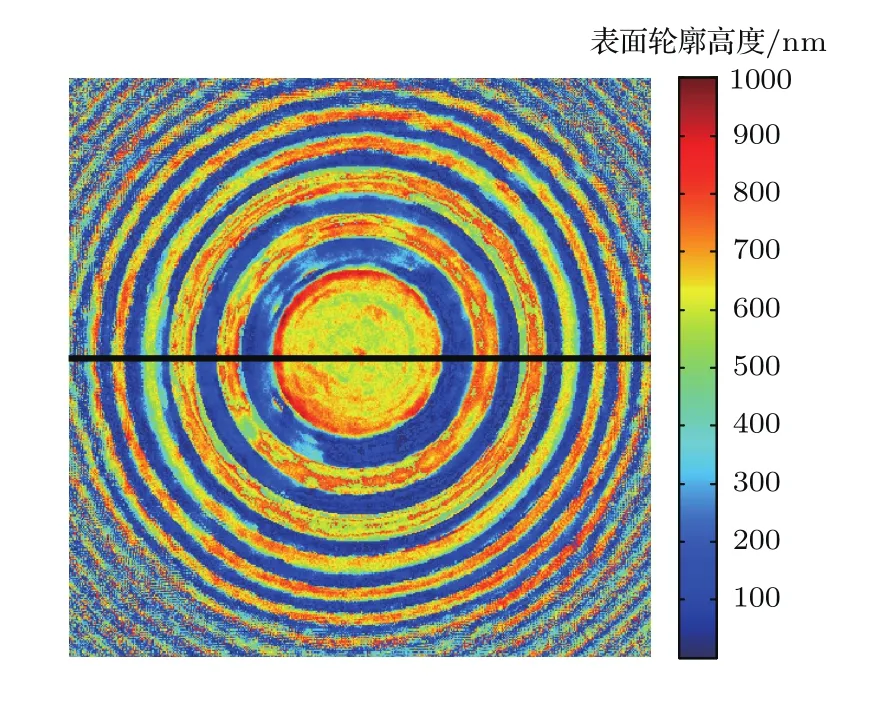
图6 (网刊彩色)表面轮廓检测CGH样品复原结果Fig.6.(color online)Reconstruction of the CGH in surface defect.

由图6的复原结果可以清晰地看出样品CGH的表面微观轮廓.由于CCD靶面大小限制了可采集衍射图样的大小,从而限制了复原结果有效区域的大小,实验中仅通过采集的49幅衍射图样就可实现有效区域为1.98 mm×1.98 mm的CGH的表面微观轮廓检测.若选择更大靶面的CCD,扫描阵列更大,采集更多的衍射图样信息完全可以复原出大尺寸的二元光学元件并完成表面微观轮廓检测.

图7 CGH样品横截面复原结果Fig.7.Recovery cross-section of CGH.

图7给出了图6黑线处横截面的台阶变化情况.从复原结果来看,CGH的表面微观轮廓与台阶变化的基本信息得以复原,但是精度不高.当照明光场较大时,CCD采集的单幅衍射图样所包含的信息也会更多.采集的相干衍射图是由待测元件不同区域因衍射作用信息的混叠形成的,CCD靶面的限制、采集噪声的干扰以及台阶突变区域采样点过少等容易造成衍射图样高频信息的丢失.这都是无法复原出样品的细节信息、复原结果精度不高的原因.因此大照明光场时很难实现对CGH特征尺寸台阶高度的标定.

4.2特征尺寸台阶高度的标定

图8 (网刊彩色)(a)台阶高度标定CGH样品复原结果;(b)CGH横截面曲线图;(c)白光干涉仪检测结果;(d)白光检测CGH横截面曲线图Fig.8.(color online)(a)Reconstruction of the CGH in step height calibration;(b)cross-section of CGH;(c)test result obtained from the white light interference microscope;(d)cross-section of CGH obtained from the white light interference microscope.

实验系统中照明光场的尺寸是可变的,为了在复原表面微观轮廓的基础上标定样品的台阶高度,需要选择合适的照明光场.实验中将光阑的直径变为1.6 mm,调整透镜到样品的距离为45 mm,估算的照明光尺寸直径约为0.8 mm,CCD放在样品后75 mm处.控制电动平移台完成对样品9×9阵列扫描,扫描步进为0.08 mm,重叠率为90%.采集的衍射图样经ePIE算法300次迭代后复原出的结果如图8(a)所示,为了更好地标定,选取黑线处的横截面数据,得到图8(b)所示的曲线.

图8(a)为样品表面微观轮廓的复原结果,复原结果较为准确地表征了样品的表面微观形貌.为了获得台阶高度的精确数值,对复原结果顶端和底端取平均值可得台阶高度值为794.7 nm.为验证检测结果的准确性,用Vecco NT9100白光轮廓仪对CGH进行检测,结果如图8(c)与图8(d)所示,台阶高度值为767.0 nm,数值误差小于30 nm,这与仿真实验的结果相符合.与白光干涉仪获得的结果相比较,叠层衍射成像复原结果在台阶突变的边缘数值与实际数值相差较大,这是ePIE算法在恢复突变相位时偏差较大造成的.虽然叠层衍射成像检测精度与白光干涉相比有差距,但叠层衍射成像检测方法的实验结构简单,操作方便,只需通过采集一系列的衍射图样就可以获得成像质量较高的检测结果.

5 结 论

本文利用叠层衍射成像技术,从仿真和实验两方面成功验证了叠层衍射成像可以用于二元光学元件的表面微观轮廓检测.仿真结果与实验结果在允许误差范围内相符合,证明本文提出的检测方法具有可行性和可靠性;实验通过改变叠层衍射成像系统的照明光场完成对二元光学元件表面微观轮廓的检测和特征尺寸台阶高度的标定,表明叠层衍射成像检测衍射光学元件的方法相比于白光干涉检测和偏振检测具有结构简单、操作方便的优点.本文提出的方法为二元光学元件的检测提供了新思路,也拓宽了叠层衍射成像技术在光学元件检测领域应用.

[1]Stone T,George N 1988Appl.Opt.27 2960

[2]Guo T,Li F,Chen J P,Fu X,Hu X T 2016Opt.Lasers Eng.82 41

[3]Coppola G,Di Caprio G,Gio ff ré M,Puglisi R,Balduzzi D,Galli A,Miccio L,Paturzo M,Grilli S,Finizio A,Ferraro P 2010Opt.Lett.35 3390

[4]Chen X G,Liu S Y,Zhang C W,Jiang H,Ma Z C,Sun T Y,Xu Z M 2014Opt.Express22 15165

[5]Rodenburg J M,Hurst A C,Cullis A G 2007Ultramicroscopy107 227

[6]Sun J S,Zhang Y Z,Chen Q,Zuo C 2016Acta Opt.Sin.36 1011005(in Chinese)[孙佳嵩,张玉珍,陈钱,左超2016光学学报36 1011005]

[7]Thibault P,Dierolf M,Bunk O,Menzel A,Pfei ff er F 2009Ultramicroscopy109 338

[8]Hoppe W 1969Acta Cryst.A25 495

[9]Fienup J R 1982Appl.Opt.21 2758

[10]Rodenburg J M,Faulkner H M L 2004Appl.Phys.Lett.85 4795

[11]Maiden A M,Rodenburg J M 2009Ultramicroscopy109 1256

[12]Pan X C,Veetil S P,Liu C,Lin Q,Zhu J Q 2013Chin.Opt.Lett.11 021103

[13]Maiden A M,Humphry M J,Zhang F C,Rodenburg J M 2011J.Opt.Soc.Am.A28 604

[14]Rodenburg J M,Hurst A C,Cullis A G,Dobson B R,Pfei ff er F,Bunk O,David C,Je fi movs K,Johnson I 2007Phys.Rev.Lett.98 034801

[15]Claus D,Maiden A M,Zhang F C,Sweeney F G,Humphry M J,Schluesener H,Rodenburg J M 2012Opt.Express20 9911

[16]Liu X L,Pan Z,Wang Y L,Shi Y S 2015Acta Phys.Sin.64 234201(in Chinese)[刘祥磊,潘泽,王雅丽,史祎诗2015物理学报64 234201]

[17]Wang Y L,Li T,Gao Q K,Zhang S G,Shi Y S 2013Opt.Eng.52 091720

[18]Claus D,Robinson D J,Chetwynd D G,Shuo Y,Pike W T,José J D J,Rodenburg J M 2013J.Opt.15 035702

[19]Tao H,Veetil S P,Cheng J,Pan X C,Wang H Y,Liu C,Zhu J Q 2015Appl.Opt.54 1776

[20]Wang H Y,Liu C,Veetil S P,Pan X C,Zhu J Q 2014Opt.Express22 2159

[21]Wang Y L,Shi Y S,Li T,Gao Q K,Xiao J,Zhang S G 2013Acta Phys.Sin.62 064206(in Chinese)[王雅丽,史祎诗,李拓,高乾坤,肖俊,张三国2013物理学报62 064206]

[22]Hüe F,Rodenburg J M,Maiden A M,Midgley P A 2011Ultramicroscopy111 1117

[23]Humphry M J,Kraus B,Hurst A C,Maiden A M,Rodenburg J M 2012Nat.Commun.3 730

[24]Rodenburg J M,Hurst A C,Maiden A M 2010J.Phys.:Conf.Ser.241 012003

PACS:42.30.–d,42.25.Fx,42.30.Rx,42.30.KqDOI:10.7498/aps.66.094201

Detection of the binary optical element based on ptychography∗

Wang Lei1)Dou Jian-Tai1)Ma Jun1)†Yuan Cao-Jin2)Gao Zhi-Shan1)Wei Cong1)Zhang Tian-Yu1)

1)(School of Electronic and Optical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)2)(Department of Physics,Nanjing Normal University,Nanjing 210097,China)

8 November 2016;revised manuscript

30 December 2016)

Due to the extremely high di ff ractive efficiency and fl exible design freedom,binary optical element can realize speci fi c function in the optical system in comparison with the traditional refractive optical element.Ptychography,which is a typical lensless optical imaging technology with simple structure,has the advantages of the extensible imaging range and high resolution.The topography of binary optical element can produce the phase di ff erence between the illumination and transmission fi elds.The features of binary optical element are based on the complex amplitude modulation.So we can obtain the complex transmission function by using ptychography to realize the phase retrieval.In this paper,we propose a detection method for binary di ff ractive optical element based on ptychography.An improved ptychography optical system is designed by using the combination of variable aperture and lens to control the illumination fi eld.Because the illumination fi eld is a diverging spherical wave,the di ff ractive patterns can avoid the high contrast and the reconstruction result will contain more details of the sample.The proposed method can not only inspect a large region of the binary optical element,but also calibrate its feature size,such as step height.Compared with the traditional binary optical element detection methods,the proposed method can simplify the system structure,and it can be applied to special environment by using lensless imaging technology.The increasing of the di ff raction pattern numbers can acquire the topography of the large size sample and improve the detection efficiency.Taking a phase step plate for sample,the simulations are conducted to analyze the in fl uences of step height and noise on the recovery result.The results show that the detection range of step height is less than 1.5λ.We can realize a preferable sample reconstruction when the noise of di ff raction pattern is less than 5%.A computer-generated holography(CGH)is reconstructed by using the extended ptychographic iterative engine.The diameter of illumination fi led is selected to be about 2 mm in order to obtain a large detection region of the sample.The surface micro topography of CGH can be shown through the 1.98 mm×1.98 mm recovery result.More details can be obtained by changing the diameter of illumination fi led about 1.6 mm.The recovery result is quite accurate and the error of step height is less than 30 nm compared with the result of white light interference detection.The simulation and experimental results verify the feasibility of this method.When the requirement for accuracy is not extremely high,the proposed method can obtain a satisfactory image quality.In addition,we hope to improve the proposed method,which can be more accurate to detect di ff erent types of optical elements in the future research.

ptychography,binary optical element,phase retrieval,feature size calibration

10.7498/aps.66.094201

∗国家自然科学基金(批准号:61377015,61505080,61575095)、中国科协“青年人才托举工程”(批准号:2015QNRC001)和中央高校基本科研业务费专项资金(批准号:30920130111007)资助的课题.

†通信作者.E-mail:majun@njust.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.61377015,61505080,61575095),the Young Elite Scientist Sponsorship Program by Chinese Association for Science and Technology(Grant No.2015QNRC001),and the Fundamental Research Funds for the Central Universities,China(Grant No.30920130111007).

†Corresponding author.E-mail:majun@njust.edu.cn