一种基于模态匹配的浅海波导中宽带脉冲声源的被动测距方法∗

李晓曼 张明辉2) 张海刚2)†朴胜春2) 刘亚琴 周建波

1)(哈尔滨工程大学水声工程学院,哈尔滨 150001)2)(哈尔滨工程大学水声技术重点实验室,哈尔滨 150001)

一种基于模态匹配的浅海波导中宽带脉冲声源的被动测距方法∗

李晓曼1)张明辉1)2)张海刚1)2)†朴胜春1)2)刘亚琴1)周建波1)

1)(哈尔滨工程大学水声工程学院,哈尔滨 150001)2)(哈尔滨工程大学水声技术重点实验室,哈尔滨 150001)

(2016年11月22日收到;2017年1月5日收到修改稿)

针对浅海波导中宽带脉冲声源的被动测距问题,本文在模态匹配和匹配场处理定位方法的基础上,提出了一种适用于具有液态半无限空间海底的浅海波导中声源的单水听器被动测距方法.利用warping变换可以对脉冲声源接收信号的各阶简正波实现有效分离,由此得到各阶简正波的频域信号.海底相移参数是描述海底地声参数的一个重要参量,包含了海底地声参数信息,而各阶简正波的水平波数可以通过含有海底相移参数的表达式来表达.此外,由于声速剖面对简正波的各阶水平波数具有相近的影响,因此通过对任意两阶简正波进行联合处理,可以近似消除声速剖面对简正波水平波数差的影响.任意两阶简正波的水平波数差只近似用于海底相移参数、海深以及波导中平均声速三个参数有关,可以简单、快速地计算相应拷贝场,然后通过建立代价函数并对简正波模态进行匹配,可以实现对水下脉冲声源的被动测距.与传统的模态匹配定位方法相比,本文提出的方法既不需要使用水听器阵,又可以简单、快速地计算出拷贝场.数值仿真和海上实验数据处理结果的测距误差都在10%以内,证明了该方法的有效性.

浅海波导,海底相移参数,模态匹配,被动测距

1 引 言

匹配场处理是将接收阵接收到的信号与根据选用的声场模型和已知的环境参数计算得到的拷贝场相关联,按照一定的准则计算出关联函数,并根据关联函数的取值在一定范围内优化搜索声源的空间位置,由此得到真实声源位置的估计值.匹配场处理考虑了海洋环境的影响,特别是海面和海底所形成的水声波导的影响,摒弃了传统无限大自由空间中平面波的声信号模型,对声传播模型计算得到的拷贝场与测量数据进行相关处理,基于水声波导中的声信号模型进行目标定位和探测,是传统基于平面波声场假设的波束形成方法的推广,与传统的时空信号处理方法相比性能得到明显提高.匹配场处理中需要根据不同的假设声源位置多次计算拷贝声场,计算量很大.拷贝场计算中选用的声场模型和声场计算精度均会影响声源定位准确性,此外,当拷贝声场计算中依据的海洋环境参数与实际海洋环境参数之间存在偏差时会造成环境失配,也会大大影响声源定位的准确性.模态匹配处理方法克服了匹配场处理中计算量大和环境失配的问题［1].声波在海水波导中以简正波的形式传播,基阵接收到的声压信号由多阶简正波信号叠加而成,模态匹配就是先利用模态滤波的方法分离基阵接收信号中的各阶简正波,并得到各阶简正波模态的幅度和相位信息,然后将这些信息与拷贝场对应的幅度和相位信息进行匹配,构建相应的代价函数,通过最优估计得到声源位置.与匹配场不同,模态匹配可以只对声场中的部分模态进行匹配,大大减少了计算量,也可通过选择处理对环境失配参数不敏感的模态来进行定位,以减少环境失配带来的定位误差［2].模态滤波是模态匹配的基础,它的性能直接影响模态匹配的性能.在模态匹配定位中也应用了许多不同的模态滤波的方法,目前常用的简正波模态分离方法主要有奇异值分解提取简正波模态函数的方法、频率-波束变换提取简正波模态的方法和波形匹配反消频散变换的方法等［3].Gary等［4]利用基于最小二乘法的模态滤波方法对包含声源信息的声压信号进行处理,并对信号的模态函数进行了分离和估计,通过将得到的模态函数与拷贝场相应的模态函数进行匹配,建立代价函数,实现了对窄带声源的距离和深度的测量.Lu等［5]则通过对多元垂直水听器阵接收声压信号的处理分离各阶模态,然后计算两阶模态的相关函数得到这两阶模态到达水听器的时间差,再利用模态到达时间差与群速度和收发距离之间的关系,构建相应的代价函数得到声源的距离.针对在接收阵提供的采样样本不充足时,模态分离的结果会对最终处理的测距结果造成很大的误差的问题,Collison和Dosso［6]提出了正则化的模态匹配处理方法,在对模态匹配处理方法进行了改进后将其应用到了声源的测距中.虽然文献[4—6]分别采用了不同的模态滤波方法,但他们的方法都是基于垂直水听器阵,基于垂直阵的模态分离方法虽然能够实现对声压信号模态的有效分离,但在实际海上工程应用中的难度很大.Barbara等［7]通过处理水平水听器阵的接收信号的频域相位,利用模态匹配方法实现了对声源的深度估计,理论和海上实验表明,与垂直阵相比,利用水平阵进行简正波模态分离所需的基阵长度更长、阵元个数更多.Chen和Lu［8]利用模态匹配方法实现了对移动声源的定位,分别讨论了频谱滤波、空间谱滤波和本征函数滤波三种模态滤波的方法,后两种方法分别需要水平接收阵和垂直接收阵,而第一种方法通过与多普勒频移相结合,只需要单水听器即可实现对接收信号模态的幅度和相位的估计,然后通过与拷贝场进行匹配即可实现了对声源有关参数的反演和估计,但这种方法对定点声源并不适用.Yang［9,10]提出了一种针对移动声源的基于垂直阵接收数据的模态匹配定位方法,利用已知的接收数据直接对模态波数和深度函数进行估计,这种方法虽然对环境参数没有依赖性却有两个明显的缺点,一是对信号模态阶数的估计低于实际模态阶数,二是对声源深度的估计受限于水听器的分布深度.Wang等［11]利用敏感矩阵对拷贝场进行了压缩,虽然大大减少了计算量但拷贝场的建立依然需要依赖海洋环境参数.文献[12—14]则将贝叶斯估计与匹配场处理相结合,提出了一种基于环境聚焦的测距方法,这种方法克服了环境失配对测距结果的影响,但数据的测量需要使用水平线阵.Zhao等［15]和郭晓乐等［16]利用波导不变量对接收信号的前几阶简正波进行消频散变换处理.郭晓乐等［16]提出了一种利用距离-频散参数二维平面聚焦测距与匹配模态能量定深的目标声源定位方法.这种方法不需要使用水听器阵,但在对各阶简正波的频散参数和环境的波导不变量进行估计时需要与相应环境模型计算的参数进行比对分析.

综合来看,以上关于模态匹配处理在定位方面的应用,主要存在以下两个缺点,首先是对模态的滤波需要用到接收水听器阵(水平阵和垂直阵),在实际应用中接收设备规模庞大,其次是对拷贝场的计算需要已知海水中声速剖面、海深、海底地层结构和海底地声参数等多项海洋环境参数.Warping变换是近年来广泛应用于水声领域的信号处理方法,它适用于浅海波导中宽带脉冲信号的简正波分离［17].国内外学者对warping变换在水下被动测距方面的应用进行了广泛的研究.戚聿波等［18]理论分析了海底地形水平缓变浅海波导中warping变换基础上的低频声场特征频率,提出了水平变化浅海波导中声源距离被动估计的修正方法.这种方法使用单水听器即可实现,但需要利用引导声源对环境参数进行估计.Bonnel等［19]通过warping变换对单水听器的接收信号的各阶模态进行分离后,再对各阶简正波模态的相位与拷贝场进行匹配,实现了对具有宽带脉冲声源特性的鲸鱼叫声的定位.这种定位方法虽然不需要水听器阵,但是拷贝场的计算依赖波导详细声速剖面等环境参数.声速剖面受海水中的温度、深度和盐度等因素的影响［20],不确定性较大.相对而言,海底参数虽然获取难度大却十分稳定,不随外在环境因素的变化而变化,而海底相移参数P是一个包含海底参数信息却相对容易获得的参数［21].为了克服模态匹配处理在测距方面对环境参数的依赖性,本文在利用warping变换对接收信号的各阶模态进行分离后,利用海底相移参数P与接收信号各阶模态水平波数之间的关系,对任意两阶简正波进行联合处理.由于海水中声速剖面对各阶简正波模态的水平波数具有相近的影响,那么对任意两阶简正波模态水平波数差的影响就可以近似抵消［21],所以任意两阶简正波模态的水平波数差与波导的声速剖面无关,只与海深和海水中平均声速以及海底相移参数三个稳定的参数有关.因此,可以简单快速地建立包含任意两阶简正波模态水平波数差的拷贝场,在对得到的各阶模态信号进行处理后进行模态匹配,可实现对声源的被动测距.仿真和实验数据处理证明了本文提出测距方法准确、有效.

本文的内容主要分为以下8部分:第一部分引言;第2部分介绍简正波的基本原理及其利用warping变换对各阶进行模态分离的原理;第3部分给出了利用简正波模态水平波数差进行匹配测距的基本原理;第4部分给出了简正波模态水平波数差拷贝场的计算过程;第5部分为理论仿真部分,仿真了同一环境下不同距离处对脉冲声源的测距;第6部分为实验数据处理及其结果验证,包括线性调频脉冲信号和爆炸声信号的处理;第7部分为对测量误差的分析;最后为结论.

2 简正波的基本原理及其模态分离

考虑海面坐标深度z=0,海面向下为正值的浅海海洋环境,考虑时间因子为e−iωt,满足远场条件时,根据简正波理论,声压的频域可以表示为［22]

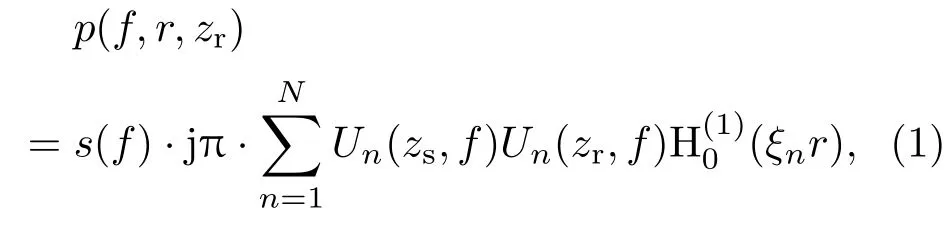
其中,s(f)为发射声源的频谱;ξn为频散方程的根,即水平波数;Un为本征函数;r为声源与水听器之间的水平距离;zs为声源的深度;zr为接收水听器的深度.又有汉克尔函数的近似表达式为

声压可以表示为

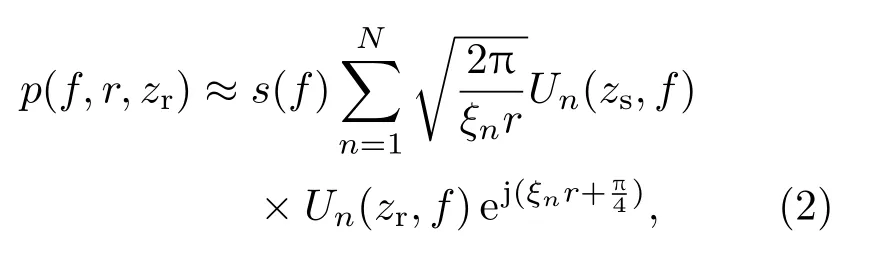
(2)式中的ξn为波导的水平波数,它与垂直波数βn和波数k(z)之间的关系如下式所示:

由于浅海波导存在多途和频散效应,参加叠加声场的各阶简正波具有不同的群速度,且每一阶简正波的群速度随着频率的变化而变化,利用声场的频散特性可以实现对各阶简正波的分离.常用的简正波分离方法为奇异值分解提取简正波模态函数方法、频率-波束变换提取简正波模态函数方法、波形匹配反消频散变换等方法,本文利用的warping变换是近年来被广泛应用的简正波模态分离技术,它是一种酉变换,适用于浅海波导且能够对单水听器的接收信号实现准确有效的分离［23].其基本理论如下［24,25].

根据简正波理论,海洋理想波导中水听器接收到的声压信号的时域表达式为

其中,tr=r0/c,r0为声源传播距离,c为波导中的平均声速,Bn(t)为第n阶简正波的瞬时幅度,fcn是第n阶简正波的截止频率.

Warping算子h(t)表示为

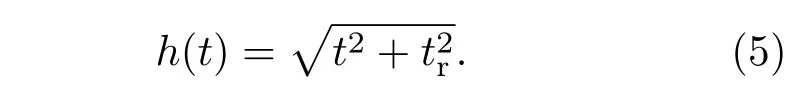
将warping算子及(4)式代入warping变换的计算公式可得到warping变换的结果:

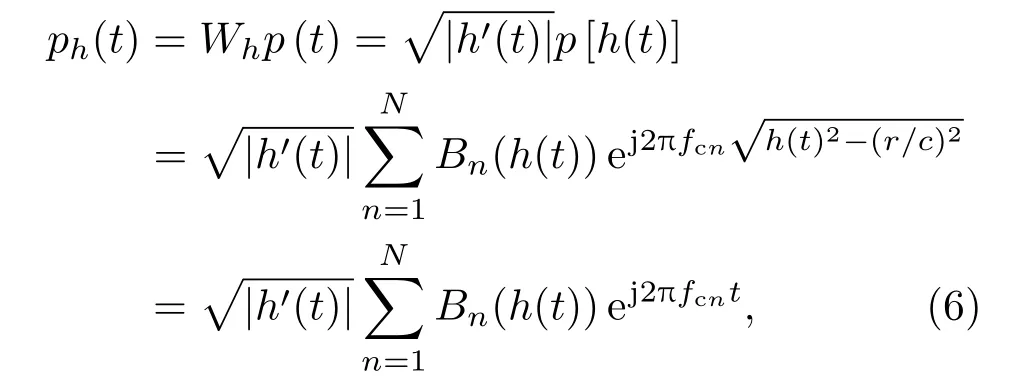
对于非理想波导,国内学者对其warping变换的公式进行了修正［26],在对接收信号的分离精度要求较高时,可以使用修正后的warping变换公式.但在本文中warping变换作为一种模态滤波的工具,处理分析的为经过warping逆变换后的还原信号,对warping变换的分离精度要求相对不高,在经典warping变换可以实现对接收信号的各阶简正波进行分离的情况下,修正后的warping变换公式和经典warping变换公式都适用.

对warping变换后的信号进行简正波分离和频域滤波后,可得到单独的某阶简正波的信息,对其做warping逆变换,获得该阶简正波原始时域信号Warping变换的逆变换算子为

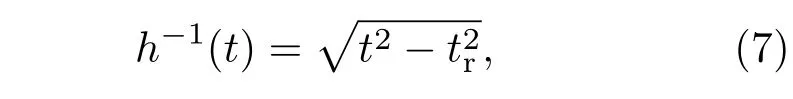
Warping逆变换可以表示为

Warping变换具有很强的稳健性,对于大部分浅海波导均适用.

3 简正波模态水平波数匹配测距的基本原理

实现对各阶简正波的有效分离后,可以得到各阶简正波的频域信息,则第n阶简正波的频域表达式为

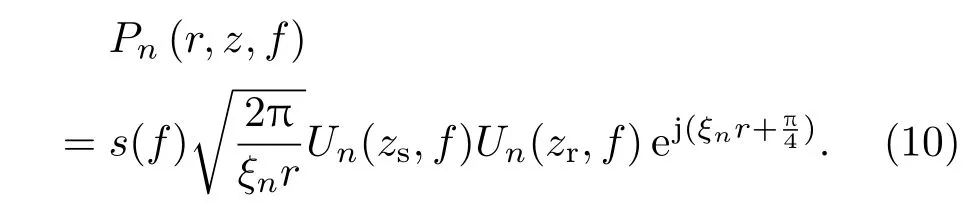
对任意两阶简正波做共轭积,可以消除声源的相位对结果的影响,任意两阶简正波(m和n阶)的共轭积为

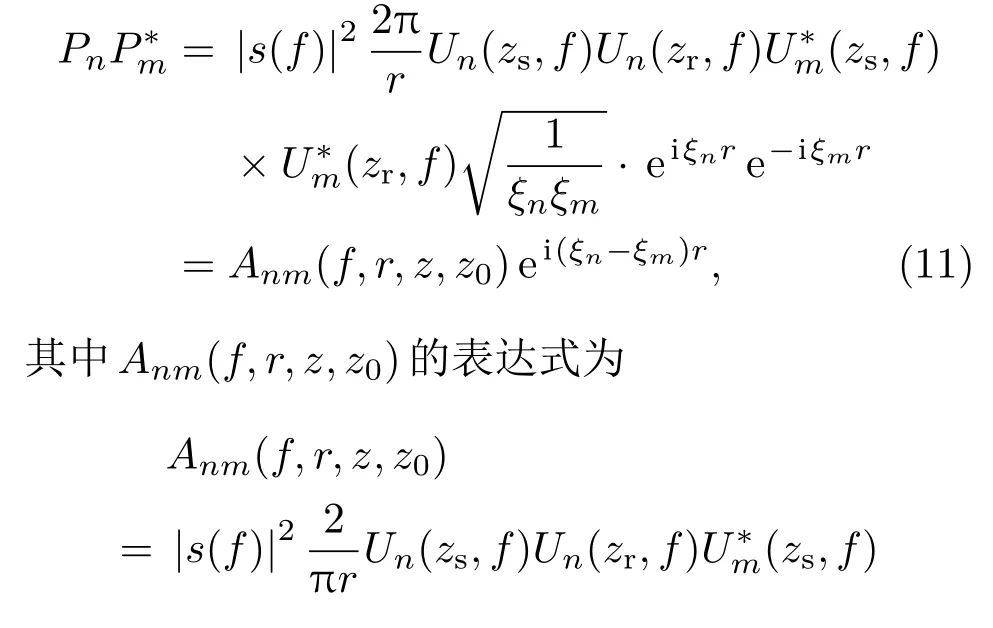
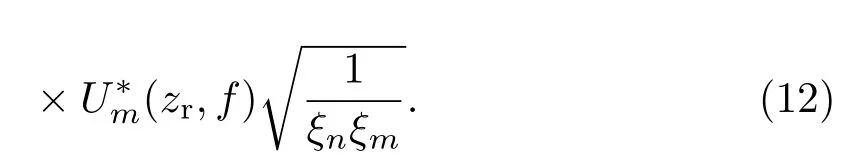
因为简正波在进行远距离传播时,频散方程的实数根(ξn的实部)对传播起主要作用,所以对于任意两阶的简正波的共轭积而言,相位部分主要是ei(ξn−ξm)r的贡献［27]. 所以,建立两阶简正波的水平波数差的相位拷贝场,对声源距离进行匹配,建立代价函数,可以实现对声源的被动测距.

在对任意两阶的简正波模态进行共轭求积后,在收发距离r未知的情况下对(11)式进行相位匹配,等号右侧乘以 e−i(ξn−ξm)r′,可以得到下式:

(13)式中r′为估计的声源距离.对于宽带信号而言,(13)式可以改写为

对不同阶数的简正波进行任意组合并求和后最终得到下式:

由(15)式可以看出,R的值受r′的影响,随r′的变化而变化.在利用warping变换对各阶模态进行分离后通过(9)式可以得到任意一阶简正波的频域声压信号.将(9)式代入(15)式,可以得到代价函数的表达式

当实际距离和估计距离相等时,即r′=r,|R|将会取得最大值,所以有|R||r=r′=|R|max.

4 简正波模态水平波数差拷贝场的计算

在计算拷贝场时,需要得到两阶简正波水平波数差值Δξnm=ξn−ξm.水平波数的获得通常依赖详细的海洋环境参数,例如海水中的声速分布以及海底环境参数,但这两者的获得需要大量的数据处理和测量工作,尤其是海水中的声速分布受到海水中的深度、温度以及盐度的影响,变化比较大,测量难度较大,容易获得的是海深和海水中的平均声速.此外,海底参数相对稳定,不随外在环境因素的变化而变化,海底相移参数是一个包含海底参数信息却相对容易获得的常数.本文利用海深和海水平均声速以及海底相移参数三个稳定的参数来表示任意两阶简正波的水平波数的差值,建立简正波模态水平波数差拷贝场.

4.1海底相移参数

根据三参数模型以及射线-简正波的基本理论［21],对于具有液态半无限海底的波导,其瑞利反射为

其中ρw,cw,ρb,cb,θ分别为海水中的密度、声速和海底的密度、声速以及声线入射角.在θ≪1(即小入射角)的情况下,有如下近似:

(18)式即为海底反射相移,而P为海底反射相移参数.P的表达式为

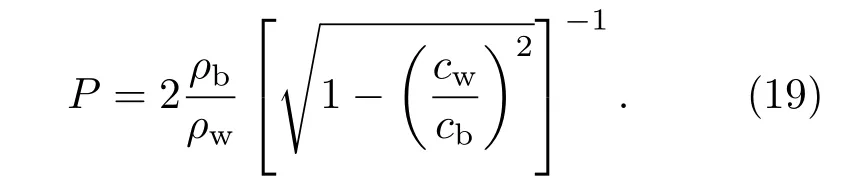
4.2拷贝场的计算

要用P来表示任意两阶简正波的水平波数差,计算相应的拷贝场,首先要得到各阶简正波的水平波数.水平波数的值由频散方程决定,具有液态半无限海底的波导的简正波类型主要是海面和海底反射类的简正波,考虑小入射角的情况,在Wentzel-Kremers-Brillouin近似下,该类波导的频散方程可以写作［28]

其中ξn为第n阶简正波的水平波数,ϕb为海底反射相移.将(18)式代入(20)式可得

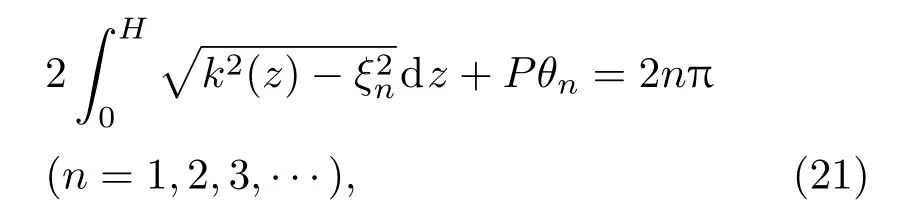
(21)式中θn为第n阶简正波的入射角,因为考虑的是小入射角的情况,所以有θn≈ sinθn,则(21)式可以化为

引入有效深度的概念,则(22)式可以化为

其中ΔH为有效深度,在不考虑剪切波的情况下,有效深度可以表示为

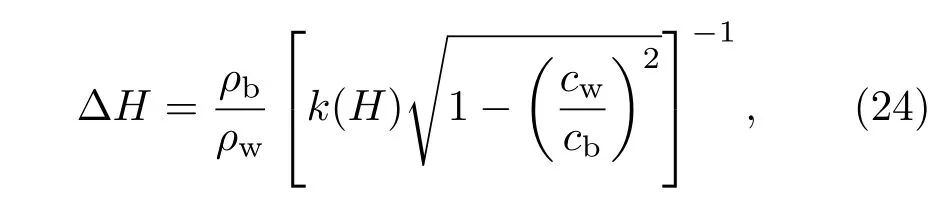
其中k(H)为海水与海底界面上海水中的波数,实际应用中可以用海水中的平均波数代替,具体验证过程将在下文中给出.结合(19)和(24)式,可以得到有效深度和海底相移参数之间的关系,两者之间的关系如下:

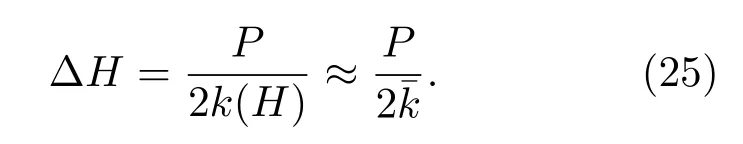
假定(20)式中k(z)为随深度变化的波数,假设海水中的声速剖面为［29]

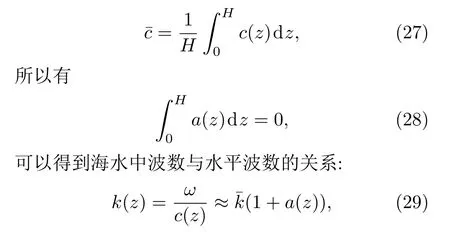
将(23)式的左侧进行泰勒级数展开并保留第一项后,(23)式可以化简为

则水平波数可以表示为［28,30]

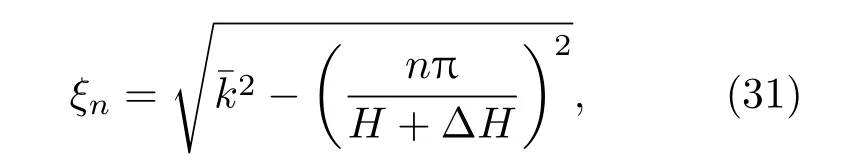
则两阶简正波的水平波数差可以表示为

由(33)式可以看到,两阶简正波的水平波数差值与海水中的声速剖面关系不大,只与海水中的平均声速、海深和海底相移参数有关.因此,可以快速计算出简正波模态水平波数差拷贝场.

4.3拷贝场的准确性验证

为了对拷贝场的准确性进行验证,本文在不同类型的声速剖面下,将通过(33)式得到的拷贝场与通过声学计算软件仿真得到的结果进行对比,同时,为了证明(25)式中海水与海底界面的海水中声速用海水中平均声速代替的合理性,也同时计算出了在ΔH=P/(2k(H))时的简正波的水平波数差值,并将其与上述两种结果进行了比较.仿真的声速剖面类型分别为正梯度声速剖面、负梯度声速剖面和含声速跃层的声速剖面,海底环境相同.仿真海深为25 m,海底声速为1700 m/s,海底密度为1.5 g/cm3,海底吸收系数为0.5 dB/λ.

声速剖面类型为正梯度声速剖面、负梯度声速剖面时,波导中海水平均声速为1500 m/s,经过计算得到海底相移参数分别为P1=6.420,P2=6.255,利用声场计算软件Kraken以及分别利用海水中的平均声速和海底海水交界面处的声速计算得到的海底相移参数进行仿真,仿真结果如图1和图2所示.

图1 (网刊彩色)正声速梯度下的ΔξnmFig.1.(color online)The Δξnmin positive sound speed pro fi le.

图2 (网刊彩色)负声速梯度下的ΔξnmFig.2.(color online)The Δξnmin negative sound speed pro fi le.

当声速剖面类型为含声速跃层时,海底相移参数的取值与接收水听器的位置有关,与声源的位置无关.当水听器位于跃层之上时,跃层界面相当于一个反射层,若跃层界面深度为H0,则参数P,H的计算依赖跃层界面上下的海洋环境参数,根据声速剖面计算得到P3_1=0,H1=H0;当水听器位于跃层之下时,参数P的计算依赖海底环境参数,经过计算得到P3_2=6.257,H2=H0.仿真结果对上述结论进行了验证说明,仿真考虑了声源、接收水听器分别位于跃层上、下时的四种不同情况,声源深度为zs,接收水听器深度为zr,仿真结果图3所示.

图1—图3给出了不同声速剖面下前5阶简正波任意两阶简正波组合时的水平波数差的计算结果,海底相移参数而由海水中平均声速¯c计算得到的结果与由海水与海底界面处的海水中声速cH计算得到的结果则几乎一致,由此可以证明(25)式是完全合理的.由图可知,根据(33)式得到的结果与声场计算软件得到的结果相比,在声速剖面不含有声速跃层时,两者符合较好;在含有声速跃层时,(33)式中的P,H的选择取决于接收水听器的位置,在正确选择P,H后,根据(33)式得到的结果与声场计算软件得到的结果两者符合较好;因此,对于含有声速跃层的浅海波导中,在仅已知海底相移参数P和海深H时,对声源的测距需要将接收水听器的位置放在跃层界面下靠近海底的位置.综上所述,根据(33)式计算得到的拷贝场准确有效.将(33)式代入(16)式,得到

(34)式为具有液态半无限空间海底的浅海波导水下声源的被动测距公式,在|R|=|R|max时,可以测得声源距离,即r′=r.

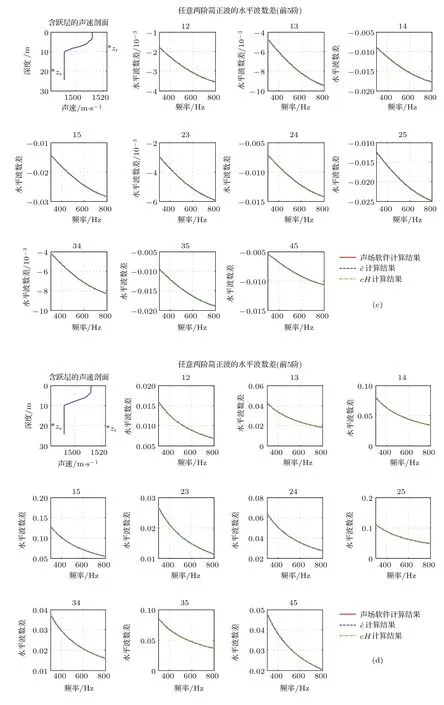
图3 (网刊彩色)含跃层的声速剖面下的Δξnm,其中,声源和接收水听器的位置为(a)zs＜H0,zr＜ H0;(b)zs＜H0,zr＞H0;(c)zs＞H0,zr＜H0;(d)zs＞H0,zr＞H0Fig.3.(color online)The Δξnmin thermocline sound speed pro fi le.The positions of source and hydrophone are:(a)zs＜H0,zr＜H0;(b)zs＜H0,zr＞H0;(c)zs＞H0,zr＜H0;(d)zs＞H0,zr＞H0.

5 理论仿真结果

5.1测距方法的理论仿真

为了验证上述测距方法的有效性,本文进行了理论仿真处理和实验数据处理.理论仿真了在同一海洋环境下不同距离声源的测距结果.发射信号为线性调频的脉冲信号,带宽为200—600 Hz,收发距离r的取值范围为5—25 km,取前五阶简正波进行处理.分别利用声学计算软件和(33)式计算拷贝场,声学软件计算得到的拷贝场为P1,本文提出方法得到的拷贝场为P2,两种拷贝场下的匹配结果和测距结果如图4所示.

利用两种方法得到的测距结果如表1所列.

由图4和表1可得,在不同距离下,直接由声学计算软件得到的拷贝场的测距结果误差低于1%,而由(33)式得到的拷贝场的测距结果误差低于3%,两种测量结果准确有效.对两种拷贝场下的测距结果进行比较,本文提出的方法得到的测距结果误差略大,但这不需要依赖大量海洋环境参数,而由声学软件计算得到的拷贝场是建立在已知海水声速剖面以及详细海底参数的基础上,因此,测量误差在可接受范围内.

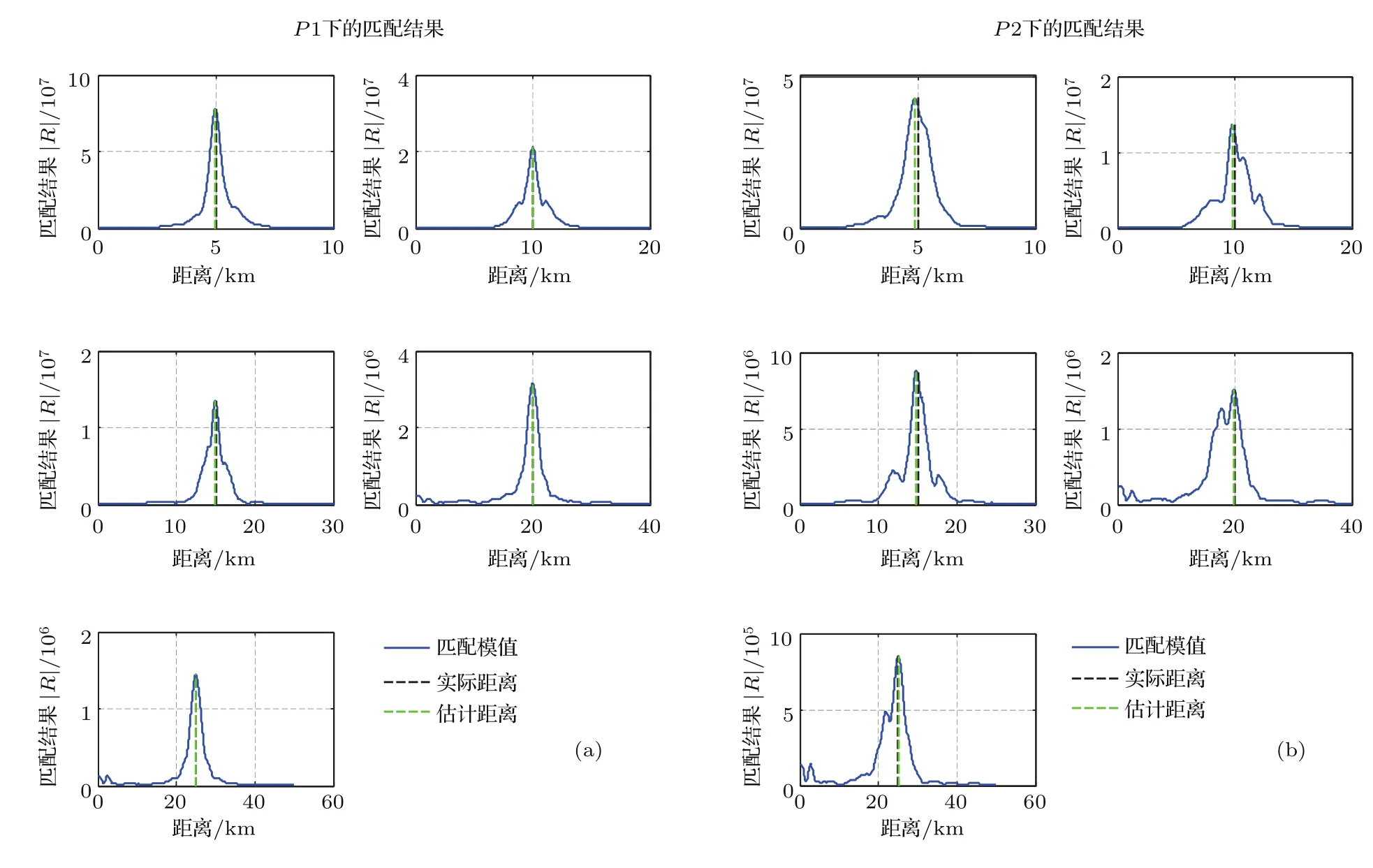
图4 (网刊彩色)两种拷贝场下的匹配结果Fig.4.(color online)The matched results in two replicas.

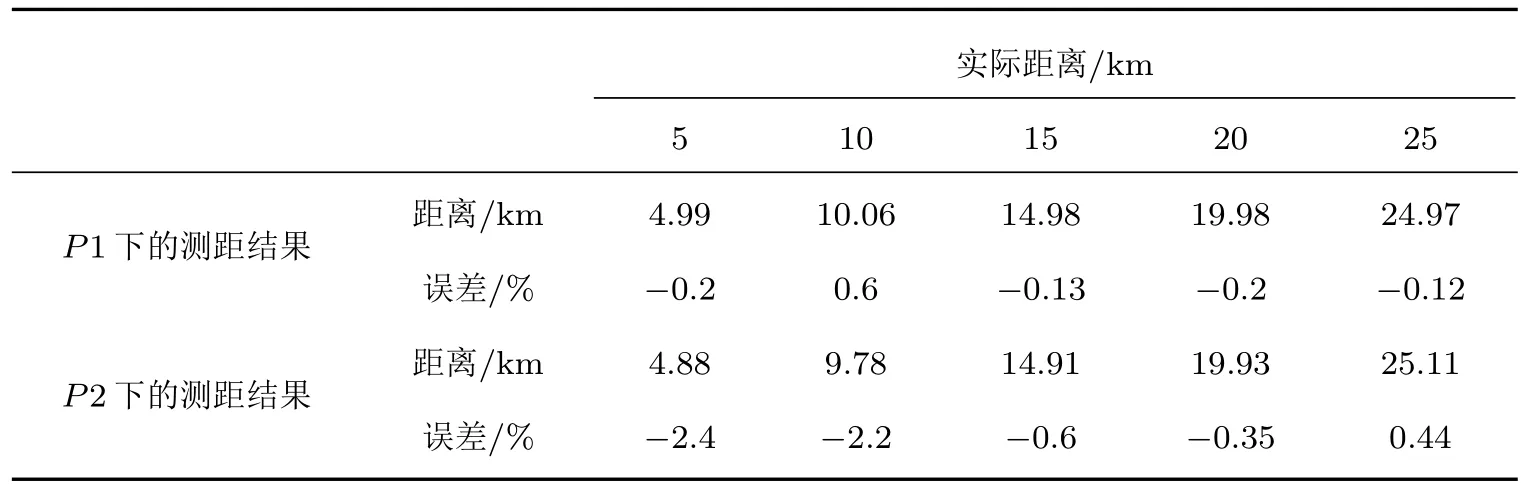
表1 两种拷贝场下的测距结果Table 1.The range results in two replicas.

5.2海深H和海底相移参数P的精度对测距结果的影响

本文提出的方法较好地解决了测距过程中声速剖面的鲁棒性问题,但在实际应用中海底声学参数和海深也是影响测距精度的重要因素,本文仿真了在不同海深H精度和海底相移P精度下的测距结果并计算得到相应的测距误差,根据得到的结果,分析了本文提出的测距方法对海深和海底相移参数精度的要求.仿真环境为pekeris波导,海深约为25 m,经过计算海底相移参数P约为6.375,收发距离r的取值范围为5—25 km,海深H和海底相移参数P的取值范围分别为[−0.9H,+1.1H]和[−0.8P,+1.2P],测距结果及其误差如图5和图6所示.

由图5和图6结果可知,本文提出的测距方法对海深的精度要求要高于海底相移参数精度的要求,在保证测距误差不超过10%的情况下,要求海深的误差在±5%以内,而对于海底相移参数的要求误差则可以在±20%内.但海深相对于海底相移参数,其测量过程简单、准确,在获得准确海深数据的情况下,对海底相移参数的宽容性大大增加了本文提出方法的适用性.

图5 (网刊彩色)不同海深精度下的测距结果和测距误差Fig.5.(color online)The range results and range errors in di ff erent accuracy of waveguide depth.

图6 (网刊彩色)不同海底相移精度下的测距结果和测距误差Fig.6.(color online)The range results and range errors in di ff erent accuracy of sea fl oor phase shift parameter.

6 实验数据处理结果

为了验证本文提出方法在实际应用的有效性,对实测实验数据进行处理.实验数据分别为两次海上试验获得,一次为利用信号源发射的线性调频信号,一次为爆炸声信号.

6.1线性调频信号实验数据处理

本次实验数据来自于2014年10月在我国黄海某海域进行的一次实验,该海域中海水的声速剖面在海深8 m处存在跃层,海水的平均声速,海深H=24.5 m,海底声速cb1≈ 1497 m/s,海底密度ρb1=1.5 g/cm3,海底衰减α1=0.05 dB/λ,使用单水听器进行信号接收,水听器接收深度zr=19 m,利用信号源发射线性调频信号,带宽为 200—600 Hz,中心频率f0=400 Hz.海底相移参数P=6.375,实验中声源的实际传播距离由GPS测得r0=4.972 km.图7为实验时的声速剖面和滤波后的接收到的时域信号,warping变换对脉冲压缩后的信号同样适用,为了方便数据处理,可对接收信号进行脉冲压缩.

对接收后的时域信号进行处理,在时频分析后,利用warping变换对其进行各阶模态的信号分离,warping变换后的结果如图8所示.

图7 (a)实验时的声速剖面;(b)接收时域信号Fig.7.(a)The sound speed pro fi le of experiment;(b)the received signal in time domain.

由图8可以看出,接收信号可以观察到的简正波模态有五阶,对这五阶简正波进行滤波分离后分别得到时域信号,再对其时域信号进行傅里叶变换就可以得到各阶简正波模态的频域信号,利用本文提出的方法对各阶简正波模态的频域信号进行处理后与拷贝场进行匹配即可对声源进行测距.为了进一步证明本文提出方法的准确性,将测量结果与通过利用海洋环境参数计算得到拷贝场时获得的测距结果进行了比较,匹配结果与测距结果如图9所示.

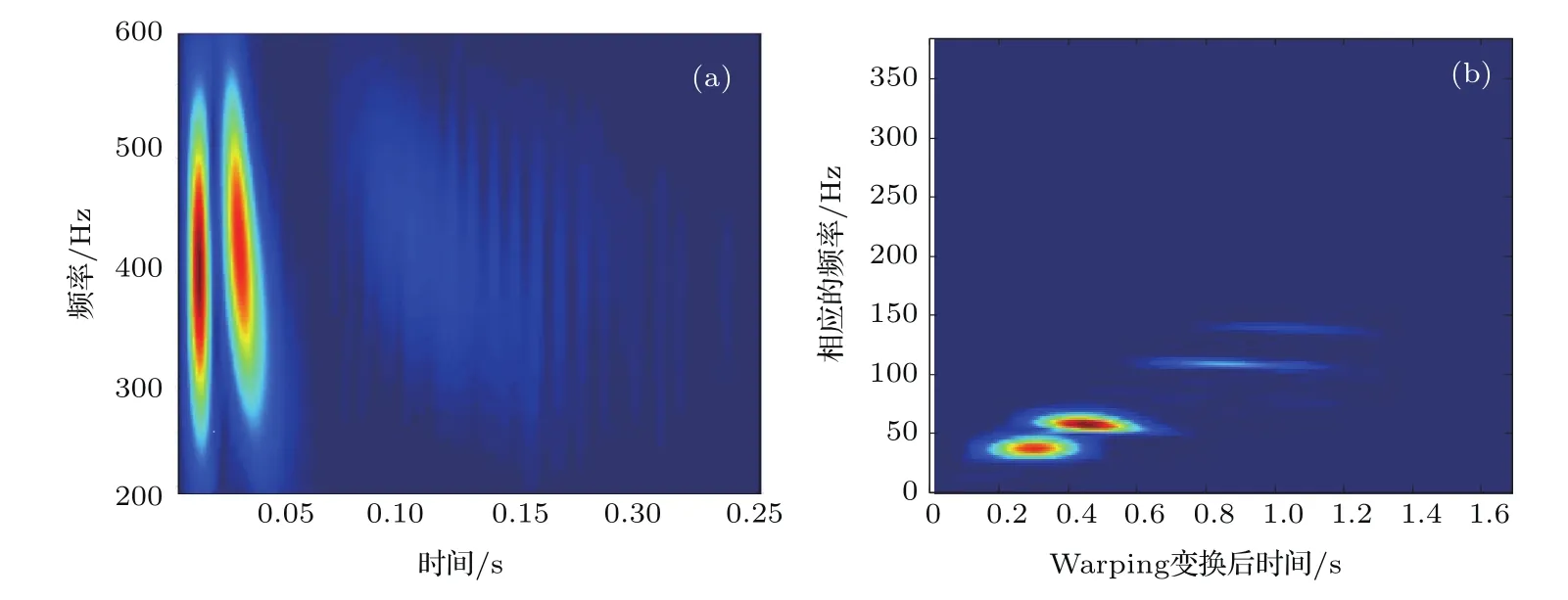
图8 (网刊彩色)(a)接收信号的时频分析及(b)warping变换结果Fig.8.(color online)(a)The time-frequency analysis results and(b)the warping transformation results of received signals.

图9 (网刊彩色)线性调频信号的匹配结果Fig.9.(color online)The matched results of linear frequency modulation signals.

6.2爆炸声实验数据处理

本次实验数据来自于2015年7月在我国黄海某海域进行的一次实验,该海域中海水的声速剖面在图10给出,海水的平均声速≈1530 m/s,海深H=35 m,海底声速cb2≈1625 m/s,海底密度ρb2=1.8 g/cm3,海底衰减α2=0.23 dB/λ,一共在38个距离投弹,使用32元垂直阵水听器对信号进行接收,本次只处理其中一个水听器的接收数据,水听器接收深度zr=25 m,爆炸声处理频段为300—600 Hz,已知海底相移参数P=10.6.

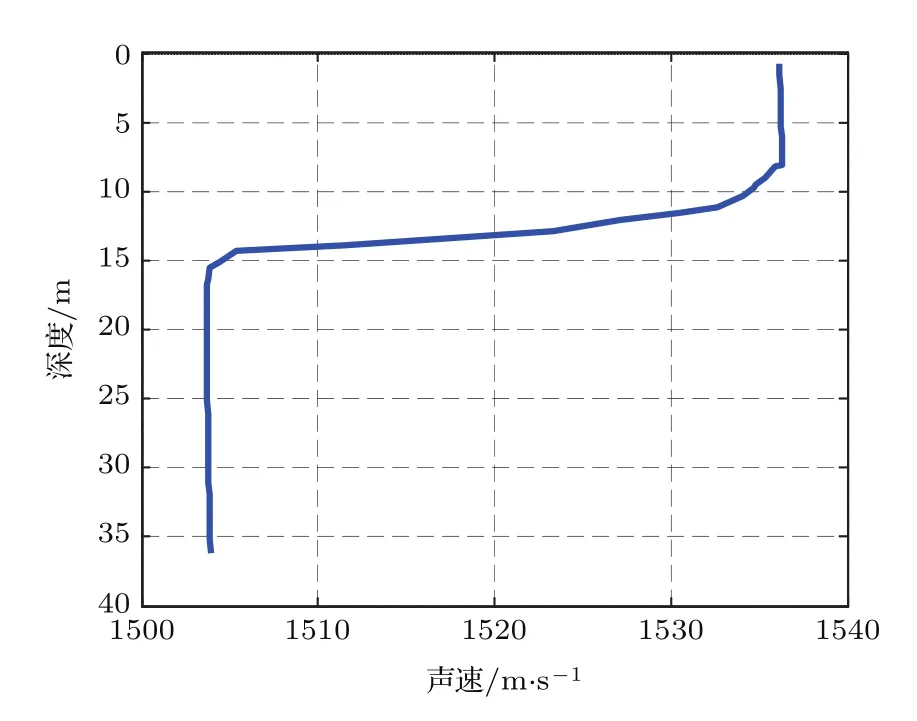
图10 爆炸声实验声速剖面Fig.10.The sound speed pro fi le of explosion sound experiment.

与上一实验数据处理过程相同,将根据(33)式得到拷贝场时的测量结果与通过利用海洋环境参数计算得到的拷贝场时获得的测距结果进行了比较,各个距离上的处理结果如图11、图12和表2所示.

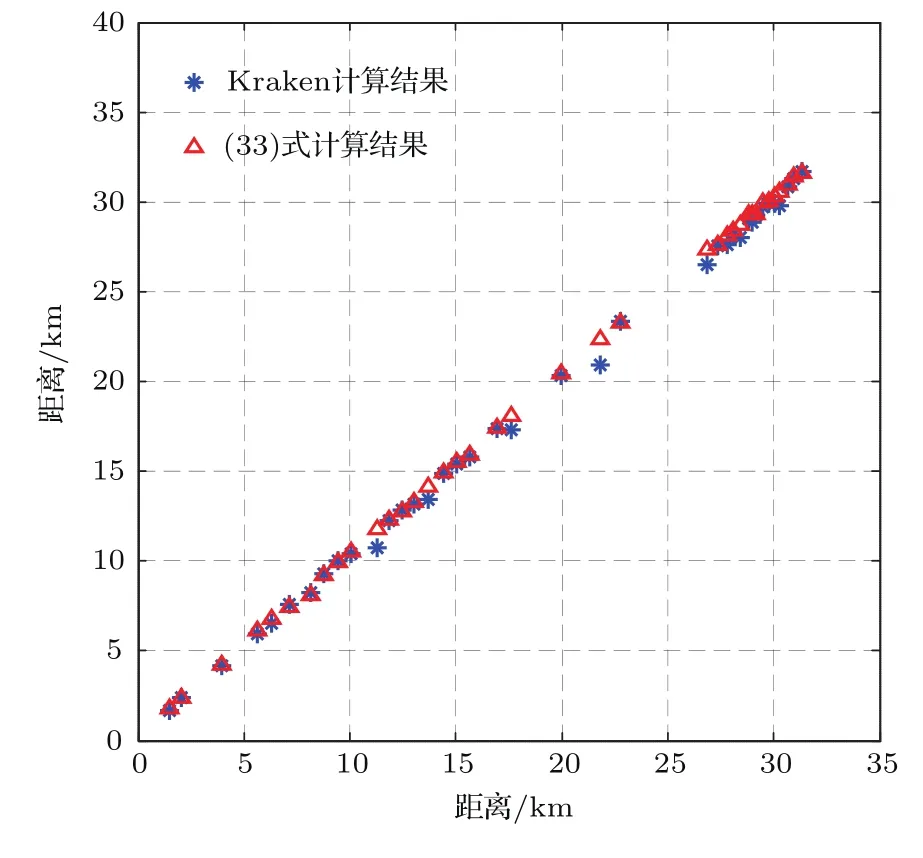
图11 (网刊彩色)爆炸声信号的测距结果Fig.11.(color online)The range results of explosion sound signals.

图12 (网刊彩色)爆炸声信号的测距误差Fig.12.(color online)The range error results of explosion sound signals.

由测量结果可以看出,前两发弹的测距结果与后面的相比,误差较大,根据实验记录,前两发弹在记录时记录仪未清零,因此这两发弹的测距结果应该舍弃.其余的测距结果误差都控制在10%以下,根据(33)式计算得到拷贝场后的测距结果与通过Kraken计算得到的拷贝场后的测距结果符合较好,测距结果可靠有效,证明了本文提出方法的准确性.同时远距离测距结果与近距离相比,误差更小,结果更准确,与仿真结果一致,说明了本文提出的测距方法的有效性.

表2 38枚弹爆炸声测距结果Table 2.The range results of 38 explosion sound signals.

7 误差分析

本文提出的方法建立在某些近似和假设的条件下,现在对于本方法测距中主要的主要误差进行分析.

对(33)式中用海水中平均声速代替海水与海底界面处海水声速带来的误差,前文已经进行了分析,分析结果表明这种情况下带来的误差几乎可以忽略不计,在此不再赘述.

由图1—图3可以看出,利用本文提出的方法计算得到的拷贝场与通过声学计算软件得到的拷贝场相比本身有一定的误差,如果将本文提出方法下得到的简正波两阶模态的水平波数差与实际水平波数差Δξnm之间的关系进行表示,则有

其中ζnm代表两者之间的差值.

对另一个误差来源(11)式进行分析,对(11)式进行进一步处理可得

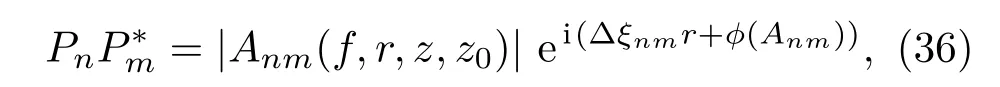
其中

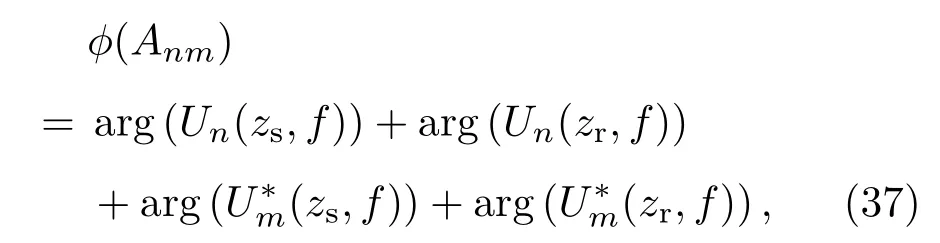
(37)式中ϕ(Anm)代表声压本征函数的相位部分,为了方便建立拷贝场且简化计算,同时考虑到在浅海波导中,本征函数的相位部分对声场的贡献很小,我们在前文中省略了这一部分相位.但由于其在实际声场中依然存在,对测距结果带来了误差.

则在(14)式中Rpnpm模值取得最大值时,将(33),(36)式与(14)式相结合,存在下式:

即此时有

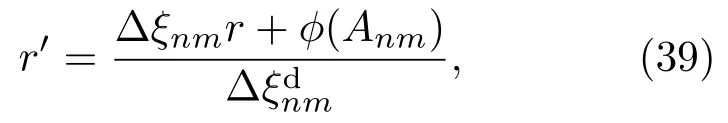
则带来的误差为

由(40)式可以看出,要想消除误差的影响一方面要构建更加完善准确的拷贝场,这在已知少量环境参数的条件下是一个挑战,另一方面就是进行远距离测距,由(40)式可知,在时,中间一项的误差可以忽略,这也同时解释了表1的测距结果中,远距离的测距结果误差更小.

8 结 论

浅海波导中宽带脉冲声源的接收信号可以利用warping变换对其各阶简正波模态进行分离,得到各阶模态频域信号.具有液态半无限海底波导的简正波类型主要是海面和海底反射类的简正波,这类简正波的水平波数与海底相移参数P具有一定的关系,海底相移参数P是描述海底地声参数的一个重要参量,包含了海底地声参数信息.在对任意两阶简正波进行联合处理后,可以近似消除海水中声速剖面对单阶简正波的影响,所以任意两阶简正波模态的水平波数差只与海深和海水中平均声速以及海底相移参数三个稳定的参数有关.因此,可以简单快速地建立包含任意两阶简正波模态水平波数差的拷贝场,再对得到的各阶模态信号进行处理后进行模态匹配,可以实现对水下脉冲声源的被动测距.与传统的匹配场定位以及模态匹配定位处理方法相比,本文提出的方法不仅不需要使用水听器阵来实现对简正波模态的分离,而且拷贝场的计算简单快速,大大减少了计算量.通过仿真和实验数据对本文提出的方法进行了验证,测距结果与实际距离相比,符合良好,测距误差均未超过10%,充分证明了测距方法准确有效.另外,本文还对引起测距误差的原因进行了分析,根据分析结果降低误差、提高测距的准确性也是接下来需要研究的重要课题.

感谢中国科学院声学研究所吴金荣老师在实验数据处理方面提供的帮助以及对文章提出的意见和建议.

[1]Huang Y W 2005Ph.D.Dissertation(Harbin:Harbin Engineering University)(in Chinese)[黄益旺 2005博士学位论文(哈尔滨:哈尔滨工程大学)]

[2]Yang T C 1990J.Acoust.Soc.Am.87 2072

[3]Yao M J,Lu L C,Ma L,Guo S M 2016Acta Acust.41 73(in Chinese)[姚美娟,鹿力成,马力,郭圣明 2016声学学报41 73]

[4]Gary R W,Robert A K,Paul J V 1988J.Acoust.Soc.Am.84 310

[5]Lu I T,Chen H Y,Voltz P 1993J.Acoust.Soc.Am.93 1365

[6]Collison N E,Dosso S E 2000J.Acoust.Soc.Am.107 3089

[7]Barbara N,Grégoire L T,Jérôme I 2008IEEE ICASSP56 2437

[8]Chen H Y,Lu I T 1992J.Acoust.Soc.Am.92 2039

[9]Yang T C 1989J.Acoust.Soc.Am.85 146

[10]Yang T C 2014J.Acoust.Soc.Am.135 1218

[11]Wang H Z,Wang N,Gao D Z,Gao B 2016Chin.Phys.Lett.33 044301

[12]Li Q Q 2016Chin.Phys.Lett.33 034301

[13]Li Q Q,Li Z L,Zhang R H 2013Chin.Phys.Lett.30 024301

[14]Peng Z H,Li Z L,Wang G X 2010Chin.Phys.Lett.27 114303

[15]Zhao Z D,Wang N,Gao D,Wang H Z 2010Chin.Phys.Lett.27 064301

[16]Guo X L,Yang K D,Ma Y L,Yang Q L 2016Acta Phys.Sin.65 214302(in Chinese)[郭晓乐,杨坤德,马远良,杨秋龙2016物理学报65 214302]

[17]Bonnel J,Chapman N R 2011J.Acoust.Soc.Am.130 101

[18]Qi Y B,Zhou S H,Zhang R H,Zhang B,Ren Y 2014Acta Phys.Sin.63 044303(in Chinese)[戚聿波,周士弘,张仁和,张波,任云2014物理学报63 044303]

[19]Bonnel J,Aaron M T,Susanna B B,Katherine K,Michael A 2014J.Acoust.Soc.Am.136 145

[20]Liu B S,Lei J Y 2010Theory of UnderwaterAcoustics(2nd Ed.)(Harbin:Harbin Engineering University Press)pp24–30(in Chinese)[刘伯胜,雷家煜 2010水声学原理(第二版)(哈尔滨:哈尔滨工程大学出版社)第24—30页]

[21]Wang D Z,Shang E C 2009Underwater Acoustics(2nd Ed.)(Harbin:Harbin Engineering University Press)pp628–640(in Chinese)[汪德昭,尚尔昌 2009水声学(第二版)(哈尔滨:哈尔滨工程大学出版社)第628—640页]

[22]Jensen F B,Kuperman W A,Porter M B,Schmidt H 1994Computational Ocean Acoustics(New York:American Institute of Physics Press)pp87–92

[23]Bonnel J,Gervaise C,Nicolas B,Mars J I 2010J.Acoust.Soc.Am.128 719

[24]Baraniuk R,Jones D 1995IEEE Trans.Signal Proc.43 2269

[25]Touze G L,Nicolas B,Mars J I 2009IEEE Trans.Signal Proc.57 1783

[26]Niu H Q 2014Ph.D.Dissertation(Beijing:University of Chinese Academy of Sciences)(in Chinese)[牛海强2014博士学位论文(北京:中国科学院大学)]

[27]Yang S E 2009Theory of Underwater Sound Propagation(Harbin:Harbin Engineering University Press)pp49–55

[28]Shang E C,Wu J R,Zhao Z D 2012J.Acoust.Soc.Am.131 3691

[29]Wang D,Guo L H,Liu J J,Qi Y B 2016Acta Phys.Sin.65 104302(in Chinese)[王冬,郭良浩,刘建军,戚聿波2016物理学报65 104302]

[30]Kevin L C,Henrik S 2011J.Acoust.Soc.Am.130 72

PACS:43.60.Jn,43.60.–c,43.30.BpDOI:10.7498/aps.66.094302

A passive range method of broadband impulse source based on matched-mode processing∗

Li Xiao-Man1)Zhang Ming-Hui1)2)Zhang Hai-Gang1)2)†Piao Sheng-Chun1)2)Liu Ya-Qin1)Zhou Jian-Bo1)

1)(College of Underwater Acoustic Engeering,Habrbin Engineering Universiy,Harbin 150001,China)2)(Acoustic Science and Technology Laboratory,Habrbin Engineering Universiy,Harbin 150001,China)

22 November 2016;revised manuscript

5 January 2017)

Aiming at the passive impulse wideband source range problem in shallow water waveguides,a passive source range method with single hydrophone based on the matched mode processing is presented in this paper,the method is applied to the shallow water waveguide with a bottom of liquid semi-in fi nite space.Warping transformation is a useful tool to separate the normal modes of the received signals of the impulse source,and the frequency domain signals of each order can be obtained.The sea fl oor phase shift parameter is an important parameter describing the acoustic parameters of the sea fl oor,which contains nearly all the information about sea fl oor,what is more,the sea fl oor phase shift parameter is also an parameter that can be obtained by some experimental data easily.Each order normal mode can be represented by the expression that contains the phase shift parameter of sea fl oor.What is more,the in fl uence of sound speed pro fi le of the waveguide on eigenvalue can be approximately eliminated by jointly processing arbitrary two-order normal modes.Sound speed pro fi le has a similar in fl uence on eigenvalue of each order normal mode,therefore,the di ff erence in the eigenvalues between arbitrary two-order normal modes can be approximated represented by the phase shift parameter of the sea- fl oor,the sea depth and the mean speed in the waveguide.In this way,the phase replica which consists of the eigenvalue di ff erence of each two-order mode can be calculated simply and quickly,and then by constructing cost function and matching normal mode,the underwater impulse source can be located.Compared with the traditional method of processing matched mode and the method of processing matched fi elds,the method presented in this paper has two advantages:using warping transformation instead of hydrophone arrays to separate the normal modes;the replica can be calculated quickly and easily,depending on a small number of environmental parameters of waveguide.The e ff ectiveness and accuracy of the method are proved by the results of numerical simulation and sea experimental data processing,in which the signals are both received by a single hydrophone.The sea experimental data contain linear frequency modulation impulse source signal and explosion sound source signal,and the mean relative error of range estimation is less than 10%.In the end of this paper,the range estimation error is analyzed,indicating that the error originates mainly from the mode phase parts besides the phase part of Hankel function.Consequently, fi nding the ways to reduce the range estimation error is an important project in the future.

shallow water waveguide,phase shift parameter,matched mode,passive range

10.7498/aps.66.094302

∗国家自然科学基金(批准号:11474073)和水声技术重点实验室开放基金(批准号:SSKF2015002)资助的课题.

†通信作者.E-mail:zhanghaigang@hrbeu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant No.11474073)and the Opening fund of Acoustics Sciences and Technology Laboratory,China(Grant No.SSKF2015002).

†Corresponding author.E-mail:zhanghaigang@hrbeu.edu.cn