教材中一道例题的一题多解
湖南省益阳市南县第一中学 卢万佳
教材中一道例题的一题多解
湖南省益阳市南县第一中学 卢万佳
衡量一名优秀的数学老师有两个重要的标准:课堂授课和解题能力,如何选题、怎样解题是每一位数学老师在教学过程中必须要认真解决的。著名美籍匈牙利数学家治·波利亚指出:“中学数学教学的首要任务就是加强解题的训练”、“解题是一种实践性技能,就像游泳、滑雪或者弹钢琴一样,只能通过模仿和实践来学到它”。
我们在解题中一定要注重解题技巧的发现,培养发散的思维,用发现的眼光去看待问题,得到更多的化解问题的方法。一题多解体现了数学解题的灵活性和多样性,这种思想的应用对数学的学习和应用是很有益处的,当学生做到举一反三的时候,就说明学生已经掌握了这一问题的解决技巧。本文通过对教材中例题的一题多解的剖析,指出学生应用一题多解的妙处。
下面对教材中例题做出具体的分析:
人教版高中数学必修2第三章第三节《点到直线的距离》一课中的例题6:已知点求△ABC的面积。
学情分析:这是学生在已学直线的方程、点到直线的距离公式的基础上提出的,教材中给出了一种直接运用公式的解法(下文中的解法一),同时在第108页右上角提出了这样一个问题:例6还有其他的解法吗?在课堂教学中很多同学积极思考,提出了很多想法。
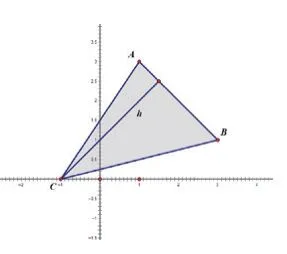
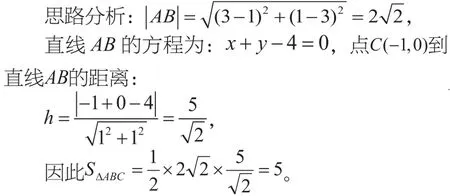
点评:直接运用公式解决问题,巩固了学生基础。
解法二:补形法(一)。
点评:通过补形发现所求的三角形面积等于两个三角形面积之差而的面积由A、B、C、D的坐标容易求出,简化了计算提高了解题的效率。
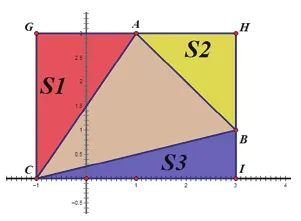
解法三:补形法(二)。
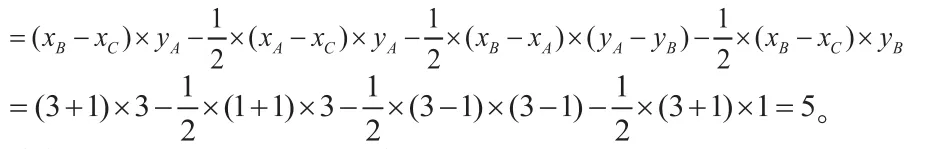
点评:通过补形发现所求的三角形面积等于矩形面积减去三个直角三角形面积,四个图形面积由A、B、C、D的坐标容易求出。
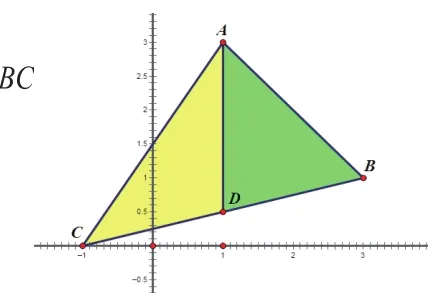
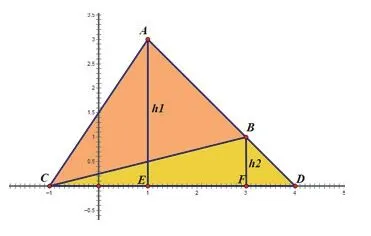
解法四:分割法。
思路分析:过点A作x轴的垂线交于点D。
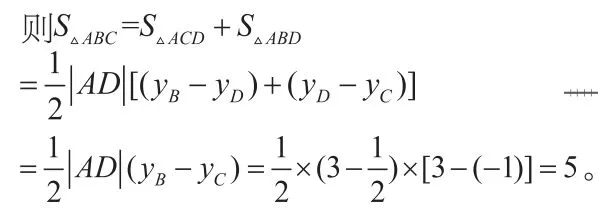
点评:通过分割图形发现所求的三角形面积等于两个三角形面积之和,而△ACD、△ABD的面积由A、B、C、D的坐标容易求出。
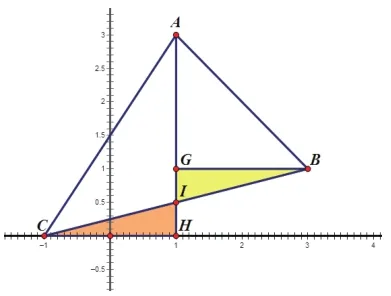
解法五:割补法。
思路分析:由解法二、四结合本题的特殊性可知:
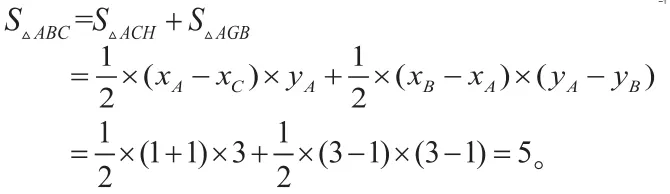
点评:通过割补图形发现所求的三角形面积等于两个直角三角形面积之和,而△ACH、△AGB的面积由A、B、C的坐标容易求出。
以上这种一题多解的例子,在我们的学习过程中,如果有意识地去分析和研究是不胜枚举的。我想:一个题目,如果这样深入观察、分析、解决和反思,那必能起到以一当十的效果。波利亚在《怎样解题》一书中指出:“学生熟悉了解个别类型问题的特殊方法以后,有可能只限于掌握一种千篇一律的死板方法而并不具备独立解决问题的本领。”通过一题多解,可以把各阶段所学的知识、知识的各个方面紧密联系起来,加深对知识的理解,认识和体会数学是一个整体,激发学习兴趣、创新意识和探索精神,培养创新能力,让学生学会学习。
一题多解有助于培养学生的发散思维能力,使学生在解题中回忆、联想所学内容,同时巩固新学的知识;有助于锻炼学生的基本技能,同时抑制教学的模型化,促进学生发展的自动化;有助于学生形成良好的数学素养,培养适应未来发展需要的学习能力。
[1]赵雄辉.数学解题思维策略——波利亚著作选讲[J].长沙:湖南教育出版社,1998.
[2]梁凤英.一道数学竞赛题的解法[J].中学数学杂志,2006(02).
[3]刘永生.数学竞赛与数学思维的发展[J].华中师范大学,2004.

