让“画图试试”成为一种经验

广东省中山市石岐张溪郑二小学 刘燕青…

让“画图试试”成为一种经验

广东省中山市石岐张溪郑二小学 刘燕青…

《数学课程标准2011年版》将“双基”修改为“四基”，明确提出让学生获得必需的基本知识、基本技能、基本思想、基本活动经验。这就要求我们的数学教学在继续保证“双基”的基础上，还必须启发学生领会数学的基本思想，积累数学活动的基本经验。在低年级教学中,笔者最常向学生推荐“画图试试”的方法，把借助画图构建知识、解决问题作为一种经验进行培养和积累。当学生在学习或解题中“山重水复疑无路”时，自觉地“画图试试”，也许就能“柳暗花明”，豁然开朗了。

低年级；画图；经验

笔者认为，培养低年级学生借助画图构建知识、解决问题的数学活动经验存在于数学各个知识领域内容的课堂教学中。

当进行概念学习时，我们“画图试试”

低年级的学生初步理解概念后，已有一定的感知经验和概念表象，但很难用准确的语言进行描述与交流。这时，教师引入结构图式，让学生“画图试试”表述的概念，可以促进学生深度理解概念，深化和发展已有的知识经验。

如，二年级的学生初步理解了“乘法”的概念后，为了让学生进一步理解乘法的意义，区分加法的意义，我们设计了先让学生“画图试试”表示“3＋4”。学生在一年级已经建立了“用括线表示一共有多少”的知识结构表象，因此大部分学生都能画出如图1的结构图式。

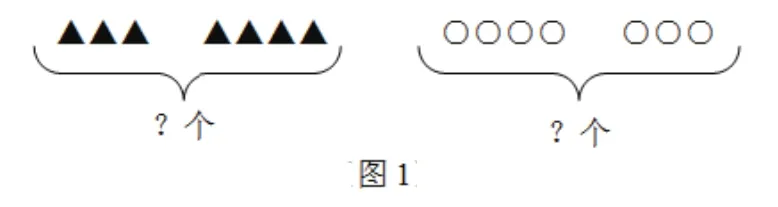
接着，让学生“画图试试”表示“3×4”。 学生在前面已初步理解了“3×4”的意义，这时让学生画图表示就是“随手拿来”了（如图2）。再观察比较“3＋4”与“3×4”的图式，加法与乘法意义的区别就一目了然，不用多费口舌了。

借助画图成功区分了加法和乘法的意义，这为学生进一步学习“乘加”的概念累积了丰富的表象和数学活动经验，再让学生“画图试试”表示“3×4＋2”就变得水到渠成了。

在以上的概念意义学习过程中，我们借助画图表达概念，把文本概念上升为结构关系概念，层层推进，促进学生对概念的深度理解、深层构建，每一次新的画图体验都以学生原有的活动经验为基础，每一次新的图式表达都是原先的活动经验的延续。

当进行几何知识学习时，我们“画图试试”

在几何知识的学习过程中，适时地让学生“画图试试”，鼓励低年级学生依据语言的描述画简单的示意图、几何草图，能帮助学生进一步理解几何知识，丰富几何表象，发展空间观念。而借助画图成功解题的经历，还能让他们从中体验画图价值，积累解题经验，为后续高年级画图策略的运用提供经验储备。

如，三年级上册有这样一道关于面积和周长计算的测试题：“把三个宽2分米，长6分米的长方形拼成一个正方形，求面积和周长各是多少？”教师先出示“求面积”，仅从文字描述解题，基本上全部学生解答为：6×2×3=36（平方分米），即用“先计算一个长方形的面积，再乘3”的方法，解答正确全体无异议。这时教师再出示“求周长呢？”受思维定式的影响，在缺少图象支撑的情况下，大部分学生解答为：(6+2)×2=24（分米），24×3=72（分米）。即用“先计算一个长方形的周长，然后乘以3”的方法计算。这时，教师提出质疑：是这样吗？我们“画图试试”吧。学生通过画图（如图3）后，隐性条件变显性，新正方形周长的表象就变得非常直观，从而沟通了三个小长方形的长与宽和大正方形的边长之间的正确联系。此时，大部分学生能有条理地思考并正确解答了。

有了上面借助画图解题的经历和体验，当学生再碰到类似的习题时，（如：把3个边长是6厘米的正方形拼成一个新的长方形，求新长方形的周长）大部分学生已能自觉主动地借助画图来解题了。

“几何直观”是2011版新课标提出的核心概念，主要是指利用图形描述和分析问题。以上让学生依据语言的描述画出图形，学生从中发现了图形相互之间的位置关系，预测出正确的结果。学生从学习经历中体验到借助图形可以使问题变得直观、简单；利用画图可以帮助发现、寻找解决问题的思路。在这个过程中不但丰富了他们的几何表象，积累画图经验，形成画图意识，更发展了学生的几何直观能力。

当解决问题时，我们“画图试试”

在解决问题过程中，当学生面对抽象的文字叙述一筹莫展时，教师可引导学生“画图试试”，让学生尝试运用自己喜欢的简单符号或图画来表达题中抽象的数量关系和变化规律，让学生借助图形符号化抽象语言为直观表象，化隐性关系为显性，理顺解题思路，从而积累运用图形符号解题的经验。

比如，在人教版一年级下册有这样一道思考题：“我们一共有10个男生。老师让相邻两个男生之间站一个女生。一共可以站进多少个女生？”一年级的学生理解、阅读、提取信息的能力较弱，对“相邻两个男生之间”的语义不明确，对“10个男生”、“相邻两个男生”、“一个女生”这三条信息之间的关系理不清。如果不引入画图而用其他直观手段：让学生排队试一试或用实物摆一摆，这样需要依托集体的力量或大量的实物，不能单靠个体独立完成。教学时，教师可以先用课件帮助学生理解“相邻两个男生之间站一个女生”，接着让学生用自己喜欢的方式“画图试试”，将信息和问题表示出来。有的学生用长方形表示男生，用圆表示女生，画出直观图（如图4）。

这幅简单的直观图，清晰地展现了题中三个信息之间的关系，理顺了解题思路，使问题迎刃而解。由此，学生初步领略到解决问题中借助图形或符号的便利，初步建立了画图解题的意识。

再如，人教版三年级下册数学广角中的等量代换，在学生学会了找中间量进行实物代换和符号代换后，教师出示书本中的一道文字代换题：“6根胡萝卜换2个大萝卜，9个大萝卜换3棵大白菜。6棵大白菜换多少根胡萝卜？”由于有了前面符号代换的学习经验，当教师提示可以用一些图形或者符号来代替题目中的信息，“画图试试”帮助解决问题时，部分学生开始主动地顺着题意设计富有个性的示意图（如图5），并尝试利用个性图画独立解题。

从这幅图可以知道，学生对问题中各种信息的结构关系已逐渐明晰，为学生思考、推理、运算提供了强有力的直观支撑，提升了学生解决问题的能力。

以上，让学生运用图形符号建构解题模型；利用图形符号进行推理运算，学生从中感受替换的数学思想，感悟到图形符号的魅力，积累到解题经验，初步建立符号意识，促进了能力发展。

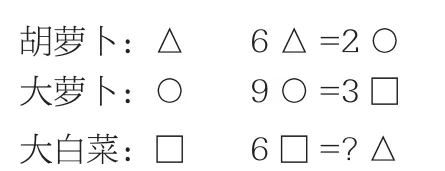
图5

综上所述，借助画图是学生积累基本数学活动经验的手段和方法之一，我们要把自觉画图作为一种意识进行培养，当学生面对抽象的概念一知半解时，“画图试试”能更加形象和直观地构建概念表象，促进概念的深度理解；当学生在学习空间几何知识时，借助画图能丰富几何表象，构建几何模型；当学生在解决问题时面对抽象的文字叙述不知从何入手时，“画图试试”能帮助分析、理顺数量关系，确定解题思路和方法。我们要让“画图试试”成为一种经验习得，帮助学生轻松、有效地学习数学。